Кинематика точки
advertisement

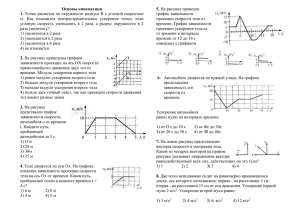
1 Механика 1 Кинематика поступательного движения и вращательного движения точки Скорость точки равна первой производной по времени от радиус-вектора (t ) dr . dt Средняя скорость ср точки равна отношению перемещения r точки к промежутку времени t , в течение которого это перемещение совершено ср r . t Ускорение а точки равно первой производной по времени от скорости a d d 2r 2 . dt dt Ускорение можно представить как сумму тангенциальной и нормальной составляющей a a an a an n , d 2 S d d 1 dS 2 a , , где S – естественная координата, ρ – радиус кривизны траектории точки, n dt 2 dt dt dt dS – тангенциальная скорость. dt x x0 x t Движение точки с постоянной скоростью ( const ): r r0 t , y y 0 y t . z z 0 z t at 2 x 0 x axt r r t a t a t Движение точки с постоянным ускорением ( a const ): , y , 0 0 0y y , 0 2 z 0 z az t a xt 2 x x0 0 xt 2 a yt 2 . y y0 0 yt 22 z z0 0 z t a z t 2 a t2 Движение точки с постоянным тангенциальным ускорением ( a const ): 0 a t , S S0 0 t . 2 d Угловая скорость : k z k dt 2 a Движение точки с постоянной угловой скоростью ( const ): 0 z t . Связь модуля угловой скорости ω с частотой вращения ν: 2 . Связь угла поворота φ – φ0 с числом оборотов N: 0 2N . d d 2 Угловое ускорение равно первой производной по времени от угловой скорости : 2 k. dt Движение точки с постоянным угловым ускорением ( const ): z 0 z zt , 0 0 zt dt zt 2 . 2 Связь между линейными и угловыми величинами: [ r ], a [ , r ] [ , ], где [ , r ] a ; a r sin( , r ) R; [, ] an ; a n sin( , ) 2 R . Скорость и ускорение при общем случае движения: р [ р , r rр ] , a a р [ р , r rр ] [ p , p ] . Закон сложения скоростей: абс. пер. отн. . Закон сложения ускорений: a абс. aотн. a пер. 2[ пер. , отн. ] . Ф1.1.1-1 Материальная точка М движется по окружности со скоростью зависимости проекции скорости направления, V – проекция V имеет направление … V от времени ( V. На рис. 1 показан график – единичный вектор положительного на это направление). При этом вектор полного ускорения на рис. 2 1. 2 2. 4* 3. 1 4. 3 Рис. 1 Рис. 2 При естественном способе ускорение точки с учётом , a d d 2 n . Из графика видно, что точка М тормозит (с dt dt увеличением времени, уменьшается). Тангенциальное ускорение а направлено в противоположную от вектора скорости d d 0, a ). Т.к. движение криволинейное, то сторону (на Рис. 1 видно, что 0, ; dt dt 2 центростремительное ускорение аn n (R – радиус окружности на Рис. 2) отлично от нуля и направлено по нормали к центру R кривизны траектории, что совпадает с направлением 3 на Рис.2. Полное ускорение а а аn . По рисунку видно, что это направление 4. Ответ: 2 Ф1.1.1-2 зависимости проекции скорости направления, V – проекция V V от времени ( V. На рис. 1 показан график 1. – единичный вектор положительного 2. Материальная точка М движется по окружности со скоростью на это направление). 3. 4. an = 0; a = 0 an > 0; a = 0* an > 0; a > 0 an > 0; a < 0 При этом для нормального a n и тангенциального a ускорения выполняются условия … Ф1.1.2-1 Точка М движется по спирали с постоянной по величине скоростью в направлении, указанном стрелкой. При этом величина полного ускорения … 1. увеличивается* 2. уменьшается 3. не изменяется d Полное ускорение а а аn . Тангенциальное ускорение а характеризует быстроту изменения модуля скорости: а . dt Так как по условию модуль скорости постоянен и , то величина а 0 (равномерное движение). Нормальное ускорение 2 аn характеризует быстроту изменения направления скорости: аn . Т.к. при движении точки М по спирали радиус кривизны траектории ρ уменьшается (см. рисунок), а модуль скорости постоянен, то аn растет. Следовательно, величина полного ускорения увеличивается. Ответ: 1 Ф1.1.2-2 Точка М движется по спирали с постоянной по величине скоростью в направлении, указанном стрелкой. При этом величина нормального ускорения … 1: уменьшается* 2: увеличивается 3: не изменяется 2 . Т.к. при движении точки М по спирали радиус кривизны траектории ρ увеличивается (см. рис.), а модуль скорости по условию постоянен, то an уменьшается. Ответ: 1 Нормальное ускорение аn характеризует быстроту изменения направления скорости: аn Ф1.1.2-3 Точка М движется по спирали в направлении, указанном стрелкой. Нормальное ускорение по величине не изменяется. При этом величина скорости … 1: уменьшается* 2: увеличивается 3: не изменяется 2 . Отсюда an . По условию аn const , из рисунка видно, что при движении точки М по спирали радиус кривизны траектории ρ уменьшается. Таким образом, скорость уменьшается. Ответ: 1 Нормальное ускорение аn характеризует быстроту изменения направления скорости: аn Ф1.1.2-4 Точка М движется по спирали в направлении, указанном стрелкой. Нормальное ускорение по величине не изменяется. При этом величина скорости … 1: увеличивается* 2: уменьшается 3: не изменяется 2 . Отсюда an . По условию аn const и из рисунка видно, что при движении точки М по спирали радиус кривизны траектории ρ увеличивается. Поэтому скорость увеличивается. Ответ: 1 Нормальное ускорение аn характеризует быстроту изменения направления скорости: аn Ф1.1.2-5 Точка М движется по спирали с постоянной по величине скоростью в направлении, указанном стрелкой. При этом величина полного ускорения … 1: уменьшается* 2: увеличивается 3: не изменяется d Полное ускорение а а аn . Тангенциальное ускорение а характеризует быстроту изменения модуля скорости: а . dt Так как по условию модуль скорости постоянен и , то величина а 0 (равномерное движение). Нормальное ускорение 2 . Т.к. радиус кривизны траектории ρ при движении точки аn характеризует быстроту изменения направления скорости: аn М по спирали увеличивается (см. рисунок), а модуль скорости постоянен, то аn уменьшается. Следовательно, величина полного ускорения уменьшается. Ответ: 1 Ф1.1.2-6 Точка М движется по спирали с постоянным по величине нормальным ускорением в направлении, указанном стрелкой. При этом проекция тангенциального ускорения на направление скорости … 1: меньше нуля* 2: равна нулю 3: больше нуля d Проекция тангенциального ускорения на ось : а . Поскольку требуется определить проекцию тангенциального dt ускорения на направление скорости, то выберем направление единичного вектора касания совпадающим с направлением 2 d скорости, тогда и а . Нормальное ускорение аn . По условию задачи аn const : при движении точки М по dt спирали радиус кривизны траектории ρ уменьшается, поэтому величина также должна уменьшаться. Следовательно d а 0 . Ответ: 1 dt Ф1.1.2-7 Точка М движется по спирали с постоянным по величине нормальным ускорением в направлении, указанном стрелкой. При этом проекция тангенциального ускорения на направление скорости … 1: больше нуля* 2: меньше нуля 3: равна нулю Ф1.1.3-1 Материальная точка движется с постоянной по величине скоростью вдоль плоской кривой. Ее полное ускорение максимально … Полное ускорение а а аn . По условию const , поэтому а 1: в т. 3 траектории* 2: в т. 1 траектории 3: в т. 2 траектории d d 0 . Следовательно а аn , а аn . По определению dt dt 2 2 2 2 . В точке 1 а1n , в точке 2 а2 n 0 , в точке 3 а3n . Т.к R > r, то а3n a1n a2n . Следовательно, полное ускорение r R a3 >a1 >a2. Таким образом, максимально a3. Ответ: 1 аn Ф1.1.3-2 Тело движется с постоянным нормальным ускорением по траектории, изображенной на рисунке 1: уменьшается 2: не изменяется 3:увеличивается* При движении в направлении, указанном стрелкой, величина скорости тела … Ф1.1.3-3 Тело движется с постоянной по величине скоростью по дуге окружности, переходящей в прямую, как показано на рисунке. 1: увеличивается, потом остается постоянной 2: уменьшается, потом увеличивается 3: увеличивается, потом уменьшается до нуля 4: постоянна, потом уменьшается до нуля* Величина нормального ускорения тела до точки А … Ф1.1.4-1 и а n - тангенциальная Если а Если а и аn 1. равномерного движения по окружности 2. прямолинейного равноускоренного движения 3. равномерного криволинейного движения ускорения, то соотношения: а 0 , аn 0 справедливы для … 4. прямолинейного равномерного движения* d d 2 Поскольку аn 0 , то радиус кривизны траектории ρ=0: движение прямолинейное. Так как а 0 , то модуль dt dt скорости const : движение равномерное. Ответ: 4 и нормальная составляющие Ф1.1.4-2 ускорения, – тангенциальная и нормальная составляющие то соотношения: а а const , аn 0 1: прямолинейного равноускоренного движения* 2: прямолинейного равномерного движения 3: равномерного движения по окружности 4: равномерного криволинейного движения справедливы для … 2 Поскольку аn 0 , то радиус кривизны траектории ρ=∞: движение прямолинейное. Так как а a const : движение равноускоренное. Ответ: 1 Если а Ф1.1.4-3 и аn – тангенциальная и нормальная составляющие ускорения, то соотношения: для … а 0 , аn const справедливы 1: равномерного движения по окружности* 2: прямолинейного равноускоренного движения 3: прямолинейного равномерного движения 4: равномерного криволинейного движения d d 2 0 , то модуль скорости const : движение равномерное. Поскольку аn const , то радиус dt dt кривизны траектории ρ=const: движение по окружности. Ответ: 1 Поскольку а Если а Ф1.1.5-1 и аn – тангенциальная и нормальная составляющие ускорения, то для 1: а 0 ; аn const * равномерного движения по окружности справедливы соотношения: Поскольку движение равномерное, то модуль скорости const : а радиус кривизны траектории ρ=const: аn Если а 2: а 0 ; аn 0 3: а a const ; аn 0 4: а 0 ; аn const d d 0 . Поскольку движение по окружности, то dt dt 2 const . Ответ: 1 Ф1.1.5-2 и аn – тангенциальная и нормальная составляющие ускорения, то для прямолинейного равноускоренного движения справедливы соотношения: 1: а a const ; аn 0 * 2: а 0 ; аn 0 3: 4: Поскольку движение прямолинейное, то радиус кривизны траектории ρ=∞: аn а 0 ; аn const а const ; аn 0 0 . Так как движение равноускоренное: 2 а a const . Ответ: 1 Ф1.1.6-1 Точка М движется по окружности с постоянным тангенциальным ускорением. Если проекция 1: увеличивается* тангенциального ускорения на направление скорости положительна, то величина нормального 2: уменьшается ускорения… 3: не изменяется Поскольку точка М движется по окружности, то радиус кривизны траектории ρ=const. По определению тангенциальное d ускорение а . Так как проекция тангенциального ускорения на направление скорости положительна, то dt 2 d d (а ) ( ) 0 ( ) 1 . Следовательно: и возрастают. Поэтому нормальное ускорение аn будет dt dt увеличиваться. Ответ: 1 Ф1.1.6-2 Точка М движется по окружности с постоянным тангенциальным ускорением. Если проекция 1: уменьшается* тангенциального ускорения на направление скорости отрицательна, то величина нормального 2: увеличивается ускорения… 3: не изменяется Поскольку точка М движется по окружности, то радиус кривизны траектории ρ=const. По определению тангенциальное d ускорение а . Так как проекция тангенциального ускорения на направление скорости отрицательна, то dt 2 d d (а ) ( ) 0 ( ) 1 . Следовательно: и уменьшаются. Поэтому нормальное ускорение аn будет dt dt уменьшаться. Ответ: 1 Ф1.1.7-1 Материальная точка М движется по окружности со скоростью зависимости проекции скорости направления, V - проекция V V от времени ( V. На рис. 1 показан график - единичный вектор положительного 1: 3* 2: 1 3: 2 4: 4 на это направление). На рис.2 укажите направление ускорения т. М в момент времени t2. Рис. 1 Рис. 2 d 2 n . В момент времени t2, как видно из графика на Рис. 1, dt 2 d 0 . Нормальное ускорение аn n (R – радиус окружности на Рис. const . При этом тангенциальное ускорение а R dt При естественном способе ускорение точки a а аn 2) отлично от нуля и направлено по нормали к центру кривизны траектории, что совпадает с направлением 3 на Рис.2. Полное ускорение а а аn также имеет направление 3. Ответ: 1 Ф1.1.7-2 Материальная точка М движется по окружности со скоростью зависимости проекции скорости V от времени ( V. На рис. 1 показан график - единичный вектор положительного 1: 4* 2: 1 3: 2 4: 3 направления, V - проекция V на это направление). На рис.2 укажите направление ускорения т. М в момент времени t3. Рис. 1 Рис. 2 d 2 n . В момент времени t3, как видно из графика на Рис. 1, dt d d 0 . При этом тангенциальное ускорение а – направлено в сторону, противоположную уменьшается и dt dt 2 направлению единичного вектора . Нормальное ускорение аn n (R – радиус окружности на Рис. 2) отлично от нуля и R При естественном способе ускорение точки a а аn направлено по нормали к центру кривизны траектории, что совпадает с направлением 3 на Рис.2. Поэтому полное ускорение а а аn имеет направление 4. Ответ: 1 Ф1.1.7-3 Материальная точка М движется по окружности со скоростью зависимости проекции скорости направления, V - проекция V V от времени ( V. На рис. 1 показан график - единичный вектор положительного 1: 3* 2: 1 3: 2 4: 4 на это направление). На рис.2 укажите направление ускорения т. М в момент времени t1. Рис. 1 Рис. 2 d 2 n . В момент времени t1, как видно из графика на Рис. 1, dt 2 d const . При этом тангенциальное ускорение а 0 . Нормальное ускорение аn n (R – радиус окружности на Рис. R dt При естественном способе ускорение точки a а аn 2) отлично от нуля и направлено по нормали к центру кривизны траектории, что совпадает с направлением 3 на Рис.2. Полное ускорение а а аn также имеет направление 3. Ответ: 1 Ф1.1.7-4 Материальная точка М движется по окружности со скоростью зависимости проекции скорости направления, V - проекция V V от времени ( V. На рис. 1 показан график - единичный вектор положительного 1: 4* 2: 1 3: 2 4: 3 на это направление). На рис.2 укажите направление ускорения т. М в момент времени t2. Рис. 1 Рис. 2 d 2 n . В момент времени t2, как видно из графика на Рис. 1, dt d d 0 . При этом тангенциальное ускорение а – направлено в сторону, противоположную уменьшается и dt dt 2 направлению единичного вектора . Нормальное ускорение аn n (R – радиус окружности на Рис. 2) отлично от нуля и R При естественном способе ускорение точки a а аn направлено по нормали к центру кривизны траектории, что совпадает с направлением 3 на Рис.2. Поэтому полное ускорение а а аn имеет направление 4. Ответ: 1 Ф1.1.7-5 Материальная точка М движется по окружности со скоростью V. На рис. 1 показан график 1: 2* 2: 1 зависимости проекции скорости направления, V - проекция V V от времени ( - единичный вектор положительного 3: 3 4: 4 на это направление). На рис.2 укажите направление ускорения т. М в момент времени t3. Рис. 1 Рис. 2 d 2 n . В момент времени t3, как видно из графика на Рис. 1, dt d d 0 . При этом тангенциальное ускорение а увеличивается и – совпадает с направлением единичного вектора . dt dt 2 Нормальное ускорение аn n (R – радиус окружности на Рис. 2) отлично от нуля и направлено по нормали к центру R При естественном способе ускорение точки a а аn кривизны траектории, что совпадает с направлением 3 на Рис.2. Поэтому полное ускорение а а аn имеет направление 2. Ответ: 1 Ф1.1.7-6 Материальная точка М движется по окружности со скоростью зависимости проекции скорости направления, V - проекция V V от времени ( V. На рис. 1 показан график - единичный вектор положительного 1: 2* 2: 1 3: 3 4: 4 на это направление). На рис.2 укажите направление ускорения т. М в момент времени t1. Рис. 1 Рис. 2 d 2 n . В момент времени t1, как видно из графика на Рис. 1, dt d d 0 . При этом тангенциальное ускорение а – совпадает с направлением единичного вектора . увеличивается и dt dt 2 Нормальное ускорение аn n (R – радиус окружности на Рис. 2) отлично от нуля и направлено по нормали к центру R При естественном способе ускорение точки a а аn кривизны траектории, что совпадает с направлением 3 на Рис.2. Поэтому полное ускорение а а аn имеет направление 2. Ответ: 1 Ф1.1.7-7 Материальная точка М движется по окружности со скоростью зависимости проекции скорости направления, V - проекция V V от времени ( V. На рис. 1 показан график - единичный вектор положительного 1: 4* 2: 1 3: 2 4: 3 на это направление). На рис.2 укажите направление ускорения т. М в момент времени t2. Рис. 1 Рис. 2 d 2 n . В момент времени t2, как видно из графика на Рис. 1, dt d d 0 . При этом тангенциальное ускорение а – направлено в сторону, противоположную уменьшается и dt dt 2 направлению единичного вектора . Нормальное ускорение аn n (R – радиус окружности на Рис. 2) отлично от нуля и R При естественном способе ускорение точки a а аn направлено по нормали к центру кривизны траектории, что совпадает с направлением 3 на Рис.2. Поэтому полное ускорение а а аn имеет направление 4. Ответ: 1 Ф1.1.7-8 Материальная точка М движется по окружности со скоростью зависимости проекции скорости направления, V - проекция V V от времени ( V. На рис. 1 показан график - единичный вектор положительного 1: 3* 2: 1 3: 2 4: 4 на это направление). На рис.2 укажите направление ускорения т. М в момент времени t3. Рис. 1 Рис. 2 d 2 n . В момент времени t3, как видно из графика на Рис. 1, dt 2 d 0 . Нормальное ускорение аn n (R – радиус окружности на Рис. const . При этом тангенциальное ускорение а R dt При естественном способе ускорение точки a а аn 2) отлично от нуля и направлено по нормали к центру кривизны траектории, что совпадает с направлением 3 на Рис.2. Полное ускорение а а аn также имеет направление 3. Ответ: 1 Ф1.1.8-1 Скорость автомобиля изменялась во времени, как показано на графике зависимости момент времени t1 автомобиль поднимался по участку дуги. V (t ) . В 1. 4* 2. 1 3. 3 4. 2 Направление результирующей всех сил, действующих на автомобиль в этот момент времени правильно отображает вектор … Из графика зависимости V (t ) видно, что рассматривается движение с переменным ускорением. Из теоремы о движении центра n масс mac Fi ( e ) следует, что направление результирующей всех сил совпадает с направлением ускорения центра масс, которое i 1 можно разложить на тангенциальную и нормальную составляющие: ас аc аcn . Выберем направление единичного вектора , совпадающим с направлением скорости центра масс автомобиля. Тогда с с . Как видно из графика, в момент времени t1 d с d с d 0 и тангенциальное ускорение ас с совпадает с направлением 5, указанном на рисунке. Нормальное dt dt dt ускорение аcn совпадает с направлением 3, указанном на рисунке. Поэтому направление ускорения центра масс автомобиля ас и направление результирующей всех сил совпадает с направлением 4, указанном на рисунке. Ответ: 1 Ф1.1.8-2 Тело брошено под углом к горизонту и движется в поле силы тяжести Земли. На рисунке изображён восходящий участок траектории данного тела. 1. 4* 2. 1 3. 2 4. 3 5. 5 Правильно изображает полное ускорение вектор … Ф1.1.9-1 Частица из состояния покоя начала двигаться по дуге окружности радиуса R=1м с постоянным угловым ускорением ε=2с-2. Отношение нормального ускорения к тангенциальному через одну секунду равно … 1. 3 2. 2* 3. 4 4. 8 5. 1 тангенциального Ускорение частицы при движении по окружности а а аn r . Модуль ускорения a r sin r R . Нормальное ускорение аn 2 R . Поскольку частица движется с постоянным угловым ускорением, то для угловой скорости справедливо уравнение 0 t . По условию в начальном состоянии частица находилась в покое, поэтому 2 2 0 0 и t , t . Для момента времени t1=1 c 1 t1 . Тогда нормальное ускорение в момент времени t1 равно а1n t 1R . В итоге отношение нормального ускорения к тангенциальному в момент времени t1 определяется по формуле: a1n a1n 2t 12R t12 (видно, что для ответа на поставленный вопрос заданное в условии значение R = 1 м является лишним). a1 a R После подстановки численных значений получает a1n 2 . Ответ: 2 a1 Ф1.1.10-1 Камень бросили под углом к горизонту со скоростью VО. Его траектория в однородном поле тяжести изображена на рисунке. Сопротивления воздуха нет. Модуль тангенциального ускорения а 1. увеличивается 2. уменьшается* 3. не изменяется на участке А-В-С … Выберем направление единичного вектора касания совпадающим с направлением скорости (тогда ). Тогда d d проекция тангенциального ускорения а . Запишем для dt dt данного случая уравнения движения и уравнения для проекций скорости камня при координатном способе при выборе декартовых осей координат, указанном на рисунке: x 0 cos t x 0 cos gt 2 y sin t 1 0 y 0 sin gt Тогда 2 для модуля скорости с учетом (1) имеем: x2 y2 02 20 gt sin g 2t 2 02 2 gy Используя полученное соотношение находим выражение для проекции тангенциального ускорения: dy 2g d g y 2 dt g y а а g 1 x2 . dt 2 02 2 gy . Для модуля тангенциального ускорения получаем: (2) Величина x 0 cos const . На участке А-В-С модуль скорости уменьшается от А 0 до А 0 cos . Поэтому, исходя из (2), модуль тангенциального ускорения на участке А-В-С будет уменьшаться. Ответ: 2 Ф1.1.10-2 Камень бросили под углом к горизонту со скоростью VО. Его траектория в однородном поле тяжести изображена на рисунке. Сопротивления воздуха нет. Тангенциальное ускорение а 2. a > 0 a < 0* 3. а 0 1. на участке А-В-С … Ф1.1.10-3 Камень бросили под углом к горизонту со скоростью V0. Его траектория в однородном поле тяжести изображена на рисунке. Сопротивления воздуха нет. 1. во всех точках одинаков 2. максимален в точках А и Е 3. максимален в точках B и D 4. максимален в точках C Модуль полного ускорения камня … Ф1.1.10-4 Два тела брошены под одним и тем же углом к горизонту с начальными скоростями VО и 2VО. Если сопротивлением воздуха пренебречь, то соотношение дальностей полёта S2/S1 равно … 1. 4* 2. 2 3. 2 4. 2 2 402 sin 2 S g sin 2 4. Дальность полета тела, брошенного с поверхности земли, определяется соотношением: S . Тогда: 2 2 0 sin 2 S1 g g 2 0 Ответ: 1 Ф1.1.11-1 Диск вращается вокруг своей оси, изменяя проекцию своей угловой скорости показано на рисунке. Z так, как 1. от t1 до t2 и от t3 до t4 2. от t1 до t2 и от t2 до t3 3. от t2 до t3 и от t3 до t4 4. от 0 до t1 и от t1 до t2* Вектор угловой скорости направлен по оси Z в интервалы времени Когда вектор угловой скорости направлен по оси Z её проекция ωz > 0. Этому условию удовлетворяют на графике моменты времени от 0 до t1 и от t1 до t2. Ответ: 4 Ф1.1.11-2 Диск радиуса R вращается вокруг вертикальной оси равноускоренно по часовой стрелке. Укажите направление вектора углового ускорения. 1: 4* 2: 3 3: 1 4: 2 Будем считать, что диск вращается по часовой стрелке, если смотреть на него сверху. Для этого случая направление его вращения указано стрелкой на рисунке. Тогда его угловая скорость будет направлена вертикально вниз. При равноускоренном движении направление углового ускорения будет совпадать с направлением угловой скорости – в данном случае угловое ускорение будет направлено вертикально вниз или по направлению 4. Ответ: 1 Ф1.1.11-3 Диск радиуса R вращается вокруг вертикальной оси равноускоренно против часовой стрелке. Укажите направление вектора углового ускорения. 1: 3* 2: 2 3: 4 4: 1 Будем считать, что диск вращается против часовой стрелки, если смотреть на него сверху. Тогда его угловая скорость будет направлена вертикально вверх. При равноускоренном движении направление углового ускорения будет совпадать с направлением угловой скорости – в данном случае угловое ускорение будет направлено вертикально вверх или по направлению 3. Ответ: 1 Ф1.1.11-4 Диск радиуса R вращается вокруг вертикальной оси равнозамедленно по часовой стрелке. Укажите направление вектора углового ускорения. 1: 3* 2: 2 3: 4 4: 1 Будем считать, что диск вращается по часовой стрелке, если смотреть на него сверху. Тогда его угловая скорость будет направлена вертикально вниз. При равнозамедленном движении направление углового ускорения будет направлено противоположно направлению угловой скорости – в данном случае угловое ускорение будет направлено вертикально вверх или по направлению 3. Ответ: 1 Ф1.1.11-5 Диск радиуса R вращается вокруг вертикальной оси равнозамедленно против часовой стрелки. Укажите направление вектора углового ускорения. 1: 4* 2: 2 3: 3 4: 1 Будем считать, что диск вращается против часовой стрелки, если смотреть на него сверху. Тогда его угловая скорость будет направлена вертикально вверх. При равнозамедленном движении направление углового ускорения будет направлено противоположно направлению угловой скорости – в данном случае угловое ускорение будет направлено вертикально вниз или по направлению 4. Ответ: 1 Ф1.1.11-6 Диск радиуса R вращается вокруг вертикальной оси равноускоренно с заданным направлением вектора углового ускорения . Укажите направление вектора линейной скорости . 1: 2* 2: 1 3: 4 4: 3 При равноускоренном движении направление угловой скорости совпадает с направлением углового ускорения (как показано на рисунке). Направление линейной скорости определяется из соотношения, связывающего линейную и угловую скорости: [R] или направление 2 в данном случае. Ответ: 1 Ф1.1.11-7 Диск радиуса R вращается вокруг вертикальной оси равноускоренно с заданным направлением вектора углового ускорения . Укажите направление вектора линейной скорости . 1: 1* 2: 2 3: 3 4: 4 При равноускоренном движении направление угловой скорости совпадает с направлением углового ускорения (направление 4). Направление линейной скорости определяется из соотношения, связывающего линейную и угловую скорости: [R] или направление 1 в данном случае. Ответ: 1 Ф1.1.11-8 Диск радиуса R вращается вокруг вертикальной оси равнозамедленно с заданным направлением вектора углового ускорения . Укажите направление вектора линейной скорости . 1: 1* 2: 2 3: 3 4: 4 При равнозамедленном движении направление угловой скорости противоположно направлению углового ускорения (направление 4). Направление линейной скорости определяется из соотношения, связывающего линейную и угловую скорости: [R] или направление 1 в данном случае. Ответ: 1 Ф1.1.11-9 Диск радиуса R вращается вокруг вертикальной оси равнозамедленно с заданным направлением вектора углового ускорения . Укажите направление вектора линейной скорости . 1: 2* 2: 1 3: 4 4: 3 При равнозамедленном движении направление угловой скорости противоположно направлению углового ускорения (направление 3). Направление линейной скорости определяется из соотношения, связывающего линейную и угловую скорости: [R] или направление 2 в данном случае. Ответ: 1 Ф1.1.12-1 Частица движется вдоль окружности радиусом 1 м в соответствии с уравнением t 2 t 6t 12 , где φ – в радианах, t – в секундах. Число оборотов, совершенных частицей 2 до остановки, равно… Обозначим момент времени, соответствующий остановки частицы, за Отсюда N1 t1 = 1 0 2 3 c. Число оборотов, 2 t12 6t1 12 2 12 2 совершённых t1. В этот момент 1Z 0 или 1Z частицей за время t1, 1: 3 2: 1 3: 9* 4: 6 d 2 2t1 6 . dt |t t1 определяется соотношением 9 . Ответ: 3 Ф1.1.12-2 Частица движется вдоль окружности радиусом 1 м в соответствии с уравнением 1: 0* 2: 4π t 2 t 6t 12 , где φ – в радианах, t – в секундах. Нормальное ускорение частицы (в 3: 16π2 через 3 с после начала движения равно… 4: 64π2 2 2 Нормальное ускорение в момент времени t1 = 3 c определяется соотношением a1n 1 R 1Z R (R – радиус окружности, по 2 м/с2) которой движется частица). Величина 1Z Z |t t1 d 2 2t1 6 . После подстановки имеем a1n 4 2 2t1 62 R 0 . dt |t t1 Ответ: 1 Ф1.1.12-3 Частица движется вдоль окружности радиусом 1 м в соответствии с уравнением 1: 4π* 2: 2π 3: 0 м/с2) через 3 с после начала движения равно… 4: 6π Тангенциальное ускорение определяется соотношением а r . Отсюда следует, что модуль тангенциального ускорения t 2 t 2 6t 12 , где φ – в радианах, t – в секундах. Тангенциальное ускорение частицы (в a r sin r R , где R – радиус окружности, по которой движется частица. Величина модуля углового ускорения d 4 const . Отсюда следует, что модуль углового ускорения есть величина постоянная и в момент времени t1 dt 2 м модуль тангенциального ускорения a1 1 R 4 2 . Ответ: 1 с Z 2 Ф1.1.12-4 Частица движется вдоль окружности радиусом 1 м в соответствии с уравнением t 2 t 6t 12 , где φ – в радианах, t – в секундах. Угловое ускорение частицы (в 2 с-2) через 3 с после начала движения равно… 1: 4π* 2: 2π 3: 0 4: 6π d 2 4 const . Отсюда следует, что модуль углового ускорения есть dt 2 рад величина постоянная и в момент времени t1 модуль тангенциального ускорения равен 1 4 2 . Ответ: 1 с Величина модуля углового ускорения Z Ф1.1.12-5 Вращение твердого тела происходит по закону движения равно… 17t 3 . Его угловое ускорение через 1 с от начала 1: 51 рад/c2* 2: 68 рад/c2 3: 17 рад/c2 4: 102 рад/c2 Ф1.1.13-1 Твердое тело начинает вращаться вокруг оси Z с угловой скоростью, проекция которой изменяется во времени, как показано на графике. 1: 21 рад* 2: 4 рад 3: 5 рад 4: 9 рад За все время вращения тело сможет повернуться относительно начального положения на максимальный угол …