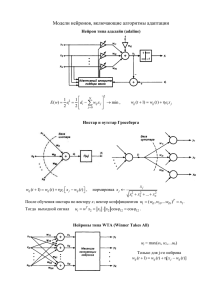
Алгоритм обучения Розенблатта
advertisement

Алгоритм обучения Розенблатта
Данный алгоритм был положен в основу обучения однослойных персептронов.
Структура персептрона Розенблатта представляется следующим образом:
x1
x2
S
A
R
S
A
R
S
A
R
...
xn
S-нейроны (сенсорные) – предназначены для формирования входных сигналов;
выполняют чисто распределительную функцию. Каждый сенсорный нейрон связан с
одним или несколькими нейронами следующего слоя (ассоциативными нейронами), при
этом каждый ассоциативный нейрон может быть связан с несколькими S-нейронами.
A-нейроны (ассоциативные) – предназначены для непосредственной обработки
входных сигналов. Выходы ассоциативных нейронов соединены с входами нейронов
третьего слоя.
R-нейроны (эффекторные) – предназначены для передачи сигналов к другим
нейронам или сетям. Нейроны этого слоя имеют несколько входов (дендритов) и один
выход (аксон), который возбуждается, если суммарная величина входных сигналов
превосходит порог срабатывания (функция активации нейронов – пороговая).
Отличия алгоритма обучения Розенблатта от алгоритма обучения по правилу
Хебба сводятся к следующему:
1.
вводится эмпирический коэффициент α с целью улучшения процесса
сходимости: α – скорость обучения 0 1 ;
2.
исключены некоторые действия, которые замедляют процесс
обучения,
например, обновление весовых коэффициентов (update).
3.
входные образы на вход НС подаются до тех пор, пока не будет достигнута
допустимая величина ошибки обучения.
4.
если решение существует, алгоритм обучения Розенблатта сходится за
конечное число шагов.
Алгоритм обучения персептрона Розенблатта заключается в настройке
коэффициентов межнейронных связей и порогов в слое A. На каждом шаге обучения, если
необходимо, происходит обновление весовых коэффициентов в соответствии со
следующей формулой.
wij (t 1) wij (t ) xi e j , (**)
где t – номер такта; i – номер нейрона во входном слое; j – номер нейрона в слое A;
α – скорость обучения; xi – входной сигнал; еj – ошибка обучения.
На каждом шаге обучения вычисляется ошибка обучения еj:
ej d j y j ,
где dj – эталонное значение входного сигнала; yj – реальное значение входного
сигнала.
Алгоритм обучения Розенблатта сводится к следующей последовательности
действий:
1.
Инициализация весовых коэффициентов и порогов значениями, близкими к
нулю.
2.
Подача на вход НС очередного входного образа (входного вектора Х), взятого
из обучающей выборки, и вычисление суммарного сигнала по всем входам для
n
каждого нейрона j: s j xi wij , где n – размерность входного вектора, xi – i-я
i 1
компонента входного вектора, wij – весовой коэффициент связи нейрона j и
входа i.
3.
Вычисление значения выхода каждого нейрона:
y j 1, если _ s j b j
, где bj – порог, соответствующий нейрону j
y j 1, если _ s j b j
ej d j y j .
4.
Вычисление значения ошибки обучения для каждого нейрона
5.
Проводится модификация весового коэффициента связи по формуле (**).
6.
Повторение пунктов 2 – 5 до тех пор, пока ошибка сети не станет меньше
заданной e j eдоп .
Особенности алгоритма обучения Розенблатта: должна быть задана скорость
обучения α и ошибка обучения е.
Пример. Воспроизведение логической функции «И» с помощью НС. Обучение НС
производится в соответствии с алгоритмом обучения Розенблатта.
Значения сигналов – биполярные: 1 и -1. Задаём скорость обучения α = 1.
Инициализируем работу НС: w11(t ) 0 _ w21(t ) 0 _ b(t ) 0
Вычисляем значение коэффициентов на каждом шаге:
w11 (t 1) w11 (t ) (d y ) x1 0 1 (1 (1)) 1 2
w11 (t 2) w11 (t 1) (d y ) x1 2 1 (1 1) 1 0
w11 (t 3) w11 (t 2) (d y ) x1 0 1 (1 1) (1) 2
w11 (t 4) w11 (t 3) (d y ) x1 2 1 (1 (1)) 1 2
w21(t i) , b(t i ) вычисляются аналогично.
b(t 1) b(t ) (d y) x3
Результаты вычислений сведём в таблицу.
шаг
t
t+1
t+2
t+3
t+4
x1
–
1
1
-1
-
x2
–
1
-1
1
-
x3
–
-1
-1
-1
-1
y
–
-1
1
1
-1
d
–
1
-1
-1
-1
w11
0
2
0
2
2
w21
0
2
4
2
2
b
0
-2
0
2
2
w11x1 w21x2 b 0
b
w
x2
11 x1 – дискриминантная линия
w21 w21
x2 x1 1
Процедура Уидроу-Хоффа
Процедура обучения Уидроу-Хоффа применима к персептронам. Уидроу и Хофф
модифицировали персептронный алгоритм Розенблатта, используя сигмоидальную
функцию активации и непрерывные выходные вектора.
Существуют два варианта реализации процедуры:
1. Adaline (Adaptive Linear Element) {Адалин}
Модель с одним выходным нейроном. Функция активации в первых вариантах
системы линейная, в последующих – сигмоидальная.
2. Madaline {Мадалин}
Модель с множественными выходными нейронами.
Процедура Уидроу-Хоффа разработана применительно к «чёрному ящику», в
котором между входами и выходами существуют только прямые связи.
n
Выход сети: y wij xi b
i 1
Процедура обучения основывается на минимизации ошибки обучения в процессе
подачи на вход сети входных образов.
L
1 L
Среднеквадратичная ошибка: E0 E k ( y k d k ) 2 , где L – число образов
2 k 1
k 1
(примеров), которые подаются на вход сети в процессе обучения.
x1
x2
xn
w1j
yj
w2j
.
.
.
wnj
Процедура заключается в градиентном спуске по настраиваемым параметрам
нейронной сети. Такими параметрами являются весовые коэффициенты и пороги сети.
Весовые коэффициенты:
Ek
wij (t 1) wij (t )
, _ j 1..m ,
wij (t )
1
где E k ( y k d k ) 2 – ошибка обучения;
2
α – скорость обучения;
m – число выходных нейронов.
Пороги:
b(t 1) b(t )
Ek
b(t )
E k
E y k
k
( y k d k ) xik , где xik – i-тая компонента k-того образа.
wij (t ) y wij (t )
E k
E y k
k
( y k d k )
b(t ) y b(t )
С учётом последних двух соотношений выражения для весовых коэффициентов и
порога примут следующий вид:
wij (t 1) wij (t ) ( y k d k ) xik
(*)
b(t 1) b(t ) ( y k d k )
Проанализировав выражения (*), можно заметить, что они идентичны
соответствующим формулам в процедуре Розенблатта в том случае, если на выходе
персептрона Розенблатта поставить пороговый элемент.
Алгоритм обучения по правилу Уидроу-Хофа сводится к следующей
последовательности действий:
1. Задаются значения параметров: скорости обучения α и допустимой ошибки
обучения Eдоп (Emin ≤ Eдоп)
2. Случайным образом инициализируются значения весовых коэффициентов и
порогов W, B.
3. На вход сети подаётся входной вектор (входной образ) X={x1, x2,..,xn} и
n
вычисляется значение выхода y wij xi b
i 1
4. Вычисляются значения весовых коэффициентов и порогов в соответствии с
формулами (*).
1
5. Вычисляется значение ошибки обучения E k ( y k d k ) 2
2
6. Проверяем выполнение условия Ek ≤ Eдоп. Если неравенство верно для всех k,
то переходим к пункту 7, в противном случае (Ek > Eдоп) – к пункту 3.
7. Останов.
Примечание: Если значение Eдоп выбрано неверно, то процесс обучения может длиться
очень долго. Поэтому целесообразно задавать число итераций вместо значения
допустимой ошибки обучения Eдоп. Обычно выбирают число итераций порядком
нескольких тысяч.
Особенности процедуры Уидроу-Хоффа (другое название – δ-правило):
с некоторыми изменениями используется в процедуре обучения многослойных
нейронных сетей
процедура применима как к дискретным, так и к непрерывным значениям
входных переменных
ошибка обучения нейронной сети минимизируется независимо от начальных
значений весов и порогов
скорость обучения сети α может меняться в зависимости от порядкового номера
такта обучения 0 1
Если выбрать скорость обучения очень маленькой, то процесс обучения будет длиться
очень долго. Если же выбрать большое значение скорости обучения, процесс стагнации
(стабилизации) может быть завершён слишком быстро, но при этом значения
коэффициентов чаще всего бывает неоптимальным. Поэтому следует искать компромисс.
Следует отметить, что на процедуру обучения влияет способ подачи образов на вход
сети. Совокупность входных образов называется «задачник».
Существенным недостатком процедуры, из-за которого при практической реализации
НС от неё отказались, является то, что в трудных задачах требуемого распределения весов
не существует.
Необходимо, чтобы в структуре «чёрного ящика» имелись некоторые промежуточные
слои. Многослойная нейронная сеть за счёт введения промежуточных слоёв позволяет
осуществить нелинейное преобразование между слоями.
x1
y
x2
x3
Функцию XOR можно реализовать с помощью сети второго порядка HON (Higher
Order Network), имеющей следующий вид:
x1
y
x2
b
x1 x2
Кроме скалярных входов имеются входы взаимодействия переменных.
Функция активации выходного нейрона – пороговая.
Для реализации функции XOR весовые коэффициенты должны иметь следующие
значения:
S w1 x1 w2 x 2 w12 x1 x 2 b
S 2 x1 2 x 2 4 x1 x 2