ЕГЭ 2011
advertisement
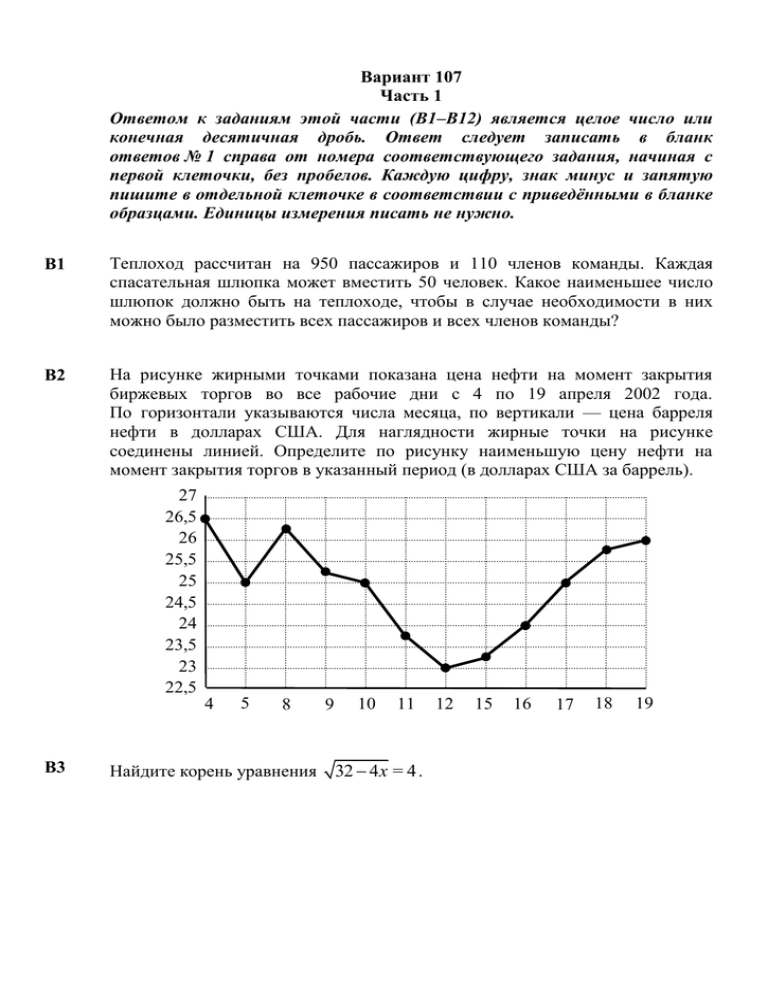
Вариант 107 Часть 1 Ответом к заданиям этой части (В1–В12) является целое число или конечная десятичная дробь. Ответ следует записать в бланк ответов № 1 справа от номера соответствующего задания, начиная с первой клеточки, без пробелов. Каждую цифру, знак минус и запятую пишите в отдельной клеточке в соответствии с приведёнными в бланке образцами. Единицы измерения писать не нужно. B1 Теплоход рассчитан на 950 пассажиров и 110 членов команды. Каждая спасательная шлюпка может вместить 50 человек. Какое наименьшее число шлюпок должно быть на теплоходе, чтобы в случае необходимости в них можно было разместить всех пассажиров и всех членов команды? B2 На рисунке жирными точками показана цена нефти на момент закрытия биржевых торгов во все рабочие дни с 4 по 19 апреля 2002 года. По горизонтали указываются числа месяца, по вертикали — цена барреля нефти в долларах США. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку наименьшую цену нефти на момент закрытия торгов в указанный период (в долларах США за баррель). 27 26,5 26 25,5 25 24,5 24 23,5 23 22,5 4 B3 5 8 Найдите корень уравнения 9 10 11 32 4 x = 4 . 12 15 16 17 18 19 B4 В треугольнике ABC AD — биссектриса, угол C равен 103 , угол CAD равен 4 . Найдите угол B . Ответ дайте в градусах. B D A B5 C В таблице указаны средние цены (в рублях) на некоторые основные продукты питания в трёх городах России (по данным на начало 2010 года). Наименование продукта Петрозаводск Белгород Новосибирск Пшеничный хлеб (батон) 13 11 15 Молоко (1 литр) 26 23 25 Картофель (1 кг) 14 10 17 Сыр (1 кг) 230 205 255 Мясо (говядина, 1 кг) 280 240 300 Подсолнечное масло (1 литр) 38 44 50 Определите, в каком из этих городов окажется самым дешёвым следующий набор продуктов: 3 л молока, 1 кг сыра, 1 л подсолнечного масла. В ответ запишите стоимость данного набора продуктов в этом городе (в рублях). B6 Найдите площадь трапеции, изображённой на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах. 1 см B7 Найдите cosα , если sin α 21 3π и α π; . 5 2 B8 На рисунке изображены график функции y f x и касательная к нему в точке с абсциссой x0 . Найдите значение производной функции f x в точке x0 . B9 Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 2. Найдите объём параллелепипеда. B10 В ходе распада радиоактивного изотопа его масса уменьшается по закону t T m(t ) m0 2 , где m0 (мг) — начальная масса изотопа, t (мин.) — время, прошедшее от начального момента, T (мин.) — период полураспада. В начальный момент времени масса изотопа m0 200 мг. Период его полураспада T 3 мин. Через сколько минут масса изотопа будет равна 25 мг? значение функции y x3 9 x 2 24 x 7 B11 Найдите наибольшее отрезке 1; 3 . на B12 Из пункта А в пункт В, расстояние между которыми 50 км, одновременно выехали мотоциклист и велосипедист. Известно, что за час мотоциклист проезжает на 30 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 1,5 часа позже мотоциклиста. Ответ дайте в км/ч. Часть 2 Для записи решений и ответов на задания С1–С6 используйте бланк ответов № 2. Запишите сначала номер выполняемого задания (С1, С2 и т.д.), а затем полное обоснованное решение и ответ. C1 Решите уравнение (4sin 2 x 12sin x 5) 17cos x 0 . C2 В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 , все рёбра которой равны 2, найдите расстояние от точки B до прямой A1F1 . C3 Решите неравенство 9log12 x 3x 4 10 log12 2 x 19 . x4 C4 Прямая, перпендикулярная гипотенузе прямоугольного треугольника, отсекает от него четырёхугольник, в который можно вписать окружность. Найдите радиус окружности, если отрезок этой прямой, заключённый внутри 5 треугольника, равен 10, а отношение катетов треугольника равно . 12 C5 Найдите все положительные значения a , при каждом из которых система x 5 2 y 4 2 9, 2 2 2 x 2 y a имеет единственное решение. C6 На доске написано более 40, но менее 48 целых чисел. Среднее арифметическое этих чисел равно 3 , среднее арифметическое всех положительных из них равно 4, а среднее арифметическое всех отрицательных из них равно 8 . а) Сколько чисел написано на доске? б) Каких чисел написано больше: положительных или отрицательных? в) Какое наибольшее количество положительных чисел может быть среди них? Критерии оценивания заданий с развёрнутым ответом C1 Решите уравнение (4sin 2 x 12sin x 5) 17cos x 0 . Решение. Если cos x 0 , то решений нет. π Если cos x 0 , то x πn, n . 2 Если cos x 0 , то 4sin 2 x 12sin x 5 0 , откуда sin x 5 2 или 1 sin x . 2 Уравнение sin x 5 не имеет решений. 2 Учитывая, cos x 0 , что из уравнения sin x 1 2 получаем: 5π 2πk , k . 6 π 5π Ответ: πn, n ; 2πk , k . 2 6 Содержание критерия Баллы Обоснованно получен верный ответ 2 Верно найдены все значения переменной x , при которых равен нулю первый сомножитель левой части исходного уравнения. Возможно 1 отбор найденных значений или не произведён, или произведён неверно Решение не соответствует ни одному из критериев, перечисленных 0 выше Максимальный балл 2 x C2 В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 , все рёбра которой равны 2, найдите расстояние от точки B до прямой A1F1 . Решение. Так как ABCDEF правильный шестиугольник, то прямые BE и AF параллельны, параллельны также прямые A1F1 и AF , следовательно, прямые A1F1 и BE параллельны. Расстояние от точки B до прямой A1F1 равно расстоянию между прямыми A1F1 и BE . A1 F1 H B В трапеции BA1F1E A1F1 2 , BE 4 , BA1 EF1 2 2 . BE A1F1 4 2 EH 1, 2 2 тогда F1H 7 . Ответ: E 7. Содержание критерия Обоснованно получен верный ответ Решение содержит обоснованный переход к планиметрической задаче, но получен неверный ответ или решение не закончено Решение не соответствует ни одному из критериев, перечисленных выше Максимальный балл C3 Решите неравенство 9log12 x 3x 4 10 log12 2 Баллы 2 1 0 2 x 19 . x4 Решение. Значения x , при которых определены обе части неравенства: x 2 3 x 4 0, x 1 x 4 0, x 19 x 19 0, 0 x4 x4 откуда x ; 1 4; . Для таких x получаем: 9 9 x 4 x 1 x 4 9log12 x 3 x 4 log12 log12 9 9 x 1 x 1 10 log12 x 4 . 10 Исходное неравенство примет вид: log12 x 4 10 . 10 Так как x 4 0 , то при условии x 4 имеем: 10 10 2 log12 x 4 10; x 4 1210 ; x 4 122 ; x 16 x 8 0, 2 x4 откуда x 8; 4 4; 16 . Учитывая, что x ; 1 4; , получаем: x 8; 1 4; 16 . Ответ: 8; 1 ; 4; 16 . Содержание критерия Баллы Обоснованно получен верный ответ 3 Обоснованно получен ответ, отличающийся от верного только конечным количеством значений переменной, при которых 2 определены обе части исходного неравенства Произведён переход от исходного неравенства к неравенствам, которые не содержат логарифмов и являются следствиями исходного 1 неравенства. Возможно ограничения, при которых исходное неравенство имеет смысл, отсутствуют или найдены неверно Решение не соответствует ни одному из критериев, перечисленных 0 выше Максимальный балл 3 C4 Прямая, перпендикулярная гипотенузе прямоугольного треугольника, отсекает от него четырёхугольник, в который можно вписать окружность. Найдите радиус окружности, если отрезок этой прямой, заключённый внутри 5 треугольника, равен 10, а отношение катетов треугольника равно . 12 Решение. Обозначим данный треугольник ABC , AB 13x — гипотенуза, AC 12 x , BC 5x . Заметим, что окружность, о которой говорится в условии, — окружность, вписанная в треугольник ABC . Пусть O — её центр, а D и E — точки касания с катетами AC и BC соответственно. Тогда, так как ODCE — квадрат, радиус этой окружности AC BC AB 12 x 5 x 13x OD EC 2x . 2 2 A M N D C O E B Рис. 1 Пусть прямая MN перпендикулярна AB , касается окружности, пересекает AB в точке M , а AC в точке N (рис. 1). Прямоугольный треугольник ANM подобен треугольнику ABC . В нём MN 10, AM 24, AN 26 . У описанного четырёхугольника суммы противоположных сторон равны: откуда 5x 10 13x 24 12 x 26 , BC MN BM CN ; находим: x 3, OD 6 . A D C O M N B Рис. 2 Пусть прямая MN перпендикулярна AB , касается окружности, пересекает AB в точке M , а BC в точке N (рис. 2). Прямоугольный 25 треугольник NBM подобен треугольнику ABC . В нём MN 10, BM , 6 65 BN . У описанного четырёхугольника суммы противоположных сторон 6 25 65 равны: AC MN AM CN ; 12 x 10 13x 5 x , откуда 6 6 25 25 находим: x , OD . 6 3 25 Ответ: 6 или . 3 Содержание критерия Баллы Обоснованно получен верный ответ 3 Рассмотрена хотя бы одна возможная геометрическая конфигурация, 2 для которой получено правильное значение искомой величины Рассмотрена хотя бы одна возможная геометрическая конфигурация, для которой получено значение искомой величины, неправильное из1 за арифметической ошибки Решение не соответствует ни одному из критериев, перечисленных 0 выше Максимальный балл 3 C5 Найдите все положительные значения a , при каждом из которых система x 5 2 y 4 2 9, 2 2 2 x 2 y a имеет единственное решение. Решение. Если x 0 , то уравнение 2 x 5 y 4 2 9 задаёт окружность ω1 с центром в точке C1 5; 4 радиуса 3 , а если x 0 , то оно задаёт окружность ω 2 с центром в точке C2 5; 4 того же радиуса (см. рис.). При положительных значениях параметра a уравнение x 2 y 2 a 2 задаёт окружность ω с центром в точке C 2; 0 радиуса a . Поэтому задача состоит в том, чтобы найти все значения параметра a , при каждом из которых окружность ω имеет единственную общую точку с объединением окружностей ω1 и ω 2 . 2 Из точки C проведём луч CC1 и обозначим A1 и B1 точки его пересечения с окружностью ω1 , где A1 лежит между C и C1 . Так как CC1 5 2 42 65 , то CA1 65 3, CB1 65 3 . При a CA1 или a CB1 окружности ω и ω1 не пересекаются. При CA1 a CB1 окружности ω и ω1 имеют две общие точки. При a CA1 или a CB1 окружности ω и ω1 касаются. 2 Из точки C проведём луч CC2 и обозначим A2 и B2 точки его пересечения с окружностью ω 2 , где A2 лежит между C и C2 . Так как CC2 5 2 42 5 , то CA2 5 3 2, CB2 5 3 8 . При a CA2 или a CB2 окружности ω и ω 2 не пересекаются. При CA2 a CB2 окружности ω и ω 2 имеют две общие точки. При a CA2 или a CB2 окружности ω и ω 2 касаются. Исходная система имеет единственное решение тогда и только тогда, когда окружность ω касается ровно одной из двух окружностей ω1 и ω 2 и не пересекается с другой. Так как CA2 CA1 CB2 CB1 , то условию задачи 2 удовлетворяют только числа a 2 и a 65 3 . Ответ: 2; 65 3 . Содержание критерия Баллы Обоснованно получен верный ответ 4 С помощью верного рассуждения получены оба верных значения параметра, но 3 – или в ответ включены также и одно-два неверных значения; – или решение недостаточно обосновано С помощью верного рассуждения получено хотя бы одно верное 2 значение параметра Задача сведена к исследованию: – или взаимного расположения трёх окружностей; 1 – или двух квадратных уравнений с параметром Решение не соответствует ни одному из критериев, перечисленных 0 выше Максимальный балл 4 C6 На доске написано более 40, но менее 48 целых чисел. Среднее арифметическое этих чисел равно 3 , среднее арифметическое всех положительных из них равно 4, а среднее арифметическое всех отрицательных из них равно 8 . а) Сколько чисел написано на доске? б) Каких чисел написано больше: положительных или отрицательных? в) Какое наибольшее количество положительных чисел может быть среди них? Решение. Пусть среди написанных чисел k положительных, l отрицательных и m нулей. Сумма набора чисел равна количеству чисел в этом наборе, умноженному на его среднее арифметическое, поэтому 4k 8l 0 m 3 k l m . а) Заметим, что в левой части каждое слагаемое делится на 4, поэтому k l m — количество целых чисел — делится на 4. По условию 40 k l m 48 , поэтому k l m 44 . Таким образом, написано 44 числа. б) Приведём равенство 4k 8l 3 k l m к виду 5l 7k 3m . Так как m 0 , получаем, что 5l 7k , откуда l k . Следовательно, отрицательных чисел больше, чем положительных. в(оценка) Подставим k l m 44 в правую часть равенства 4k 8l 3 k l m : 4k 8l 132 , откуда k 2l 33 . Так как k l 44 , получаем: 3l 33 44, 3l 77, l 25, k 2l 33 17; то есть положительных чисел не более 17. в(пример) Приведём пример, когда положительных чисел ровно 17. Пусть на доске 17 раз написано число 4, 25 раз написано число 8 и два раза 4 17 8 25 68 200 написан 0. Тогда указанный набор 3 , 44 44 удовлетворяет всем условиям задачи. Ответ: а) 44; б) отрицательных; в) 17. Содержание критерия Баллы Верно выполнены: а), б), в(пример), в(оценка) 4 Верно выполнены три пункта из четырёх: а), б), в(пример), в(оценка) 3 Верно выполнены два пункта из четырёх: а), б), в(пример), в(оценка) 2 Верно выполнен один пункт из четырёх: а), б), в(пример), в(оценка) 1 Решение не соответствует ни одному из критериев, перечисленных 0 выше Максимальный балл 4 Вариант 401 Часть 1 Ответом к заданиям этой части (В1–В12) является целое число или конечная десятичная дробь. Ответ следует записать в бланк ответов № 1 справа от номера соответствующего задания, начиная с первой клеточки, без пробелов. Каждую цифру, знак минус и запятую пишите в отдельной клеточке в соответствии с приведёнными в бланке образцами. Единицы измерения писать не нужно. B1 B2 В доме, в котором живёт Петя, один подъезд. На каждом этаже по шесть квартир. Петя живёт в квартире 45. На каком этаже живёт Петя? На рисунке жирными точками показана цена нефти на момент закрытия биржевых торгов во все рабочие дни с 4 по 19 апреля 2002 года. По горизонтали указываются числа месяца, по вертикали — цена барреля нефти в долларах США. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа цена нефти на момент закрытия торгов составила 24 доллара за баррель. 27 26,5 26 25,5 25 24,5 24 23,5 23 22,5 4 5 8 9 10 11 12 15 16 17 18 19 B3 Найдите корень уравнения log 2 (4 x) 8 . B4 В треугольнике ABC CD — медиана, угол C равен 90 , угол B равен 35 . Найдите угол ACD . Ответ дайте в градусах. C A D B B5 В первом банке один фунт стерлингов можно купить за 47,4 рубля. Во втором банке 15 фунтов — за 696 рублей. В третьем банке 22 фунта стоят 1067 рублей. Какую наименьшую сумму (в рублях) придётся заплатить за 10 фунтов стерлингов? B6 Найдите площадь треугольника, изображённого на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах. 1 см B7 Найдите значение выражения 12sin150 cos120 . B8 На рисунке изображён график y f ' x — производной функции f x , определённой на интервале 9; 8 . Найдите точку экстремума функции f x на отрезке 3; 3 . y y = f ′ (x ) −9 1 0 1 8x B9 Найдите объём многогранника, вершинами которого являются точки A, D, A1, B, C , B1 прямоугольного параллелепипеда ABCDA1B1C1D1 , у которого AB 3, AD 4, AA1 5 . B10 Зависимость температуры (в градусах Кельвина) от времени для нагревательного элемента некоторого прибора была получена экспериментально. На исследуемом интервале температура вычисляется по 14 формуле T t T0 bt at 2 , где t — время в минутах, T0 1300 К, a 3 К/мин2, b 98 К/мин. Известно, что при температуре нагревателя свыше 1720 К прибор может испортиться, поэтому его нужно отключить. Определите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ выразите в минутах. B11 Найдите наибольшее отрезке 3; 0,5 . B12 В понедельник акции компании подорожали на некоторое число процентов, а во вторник подешевели на то же самое число процентов. В результате они стали стоить на 4% дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник? значение функции y x3 2 x 2 x 7 на Часть 2 Для записи решений и ответов на задания С1–С6 используйте бланк ответов № 2. Запишите сначала номер выполняемого задания (С1, С2 и т.д.), а затем полное обоснованное решение и ответ. C1 Решите уравнение ( 3 sin x 2sin 2 x) log 6 ( tg x) 0 . C2 В правильной треугольной призме ABCA1B1C1 , все рёбра которой равны 1, найдите расстояние между прямыми AA1 и BC1 . C3 log x 2 x 1 log x 2 x 2 Решите неравенство 40 . log 2 x x log 2 x2 x C4 Точки M , K и N лежат на сторонах соответственно AB , BC и AC треугольника ABC , причём AMKN — параллелограмм, площадь которого 4 составляет площади треугольника ABC . Найдите диагональ MN 9 параллелограмма, если известно, что AB 21 , AC 12 и BAC 120 . C5 Найдите все значения a , при каждом из которых система y 5 4 x x 2 2, y 9 a 2 2ax x 2 a имеет единственное решение. C6 Можно ли привести пример пяти различных произведение которых равно 720, и а) пять; б) четыре; в) три из них образуют геометрическую прогрессию? натуральных чисел, Критерии оценивания заданий с развёрнутым ответом C1 Решите уравнение ( 3 sin x 2sin 2 x) log 6 ( tg x) 0 . Решение. Левая часть уравнения имеет смысл при tg x 0 . π Если log 6 ( tg x) 0 , то tg x 1 , откуда x πn, n . 4 2 Если log 6 ( tg x) 0 , то 3sin x 2sin x 0 , откуда sin x 0 или 3 . 2 Решения уравнения sin x 0 не являются корнями исходного уравнения. 3 Учитывая, что tg x 0 , из уравнения sin x получаем: 2 2π x 2πk , k . 3 π 2π Ответ: πn, n ; 2πk , k . 4 3 Содержание критерия Баллы Обоснованно получен верный ответ 2 Верно найдены все значения переменной x , при которых равен нулю один из сомножителей левой части исходного уравнения. Возможно 1 отбор найденных значений или не произведён, или произведён неверно Решение не соответствует ни одному из критериев, перечисленных 0 выше Максимальный балл 2 sin x C2 В правильной треугольной призме ABCA1B1C1 , все рёбра которой равны 1, найдите расстояние между прямыми AA1 и BC1 . Решение. Так как прямая BC1 пересекается с прямой BB1 , параллельной прямой AA 1 , и лежит в плоскости BCC1 , параллельной AA1 , то расстояние между прямыми AA1 и BC1 равно расстоянию от прямой AA1 до плоскости BCC1 . Пусть AK — высота треугольника ABC . AK перпендикулярна BB1 , так как BB1 перпендикулярна плоскости ABC . Таким образом, искомое расстояние — длина отрезка AK . Из равностороннего треугольника ABC находим: 3 3 3 . AK AB 1 2 2 2 3 Ответ: . 2 Содержание критерия Баллы Обоснованно получен верный ответ 2 Решение содержит обоснованный переход к планиметрической 1 задаче, но получен неверный ответ или решение не закончено Решение не соответствует ни одному из критериев, перечисленных 0 выше Максимальный балл 2 C3 log x 2 x 1 log x 2 x 2 Решите неравенство 40 . log 2 x x log 2 x2 x Решение. 1 Решение будем искать при условиях: x 0, x , x 1, x 2. 2 Для таких x получаем: log x 2 log x x 1 log x 2 log x x 2 log x 2 x 1 log x 2 x 2 1 1 log 2 x x log 2 x2 x log x 2 log x x log x 2 log x x 2 log x 2 2 log x 2 1 log x 2 1 log x 2 2 . Пусть t log x 2 . Тогда t 2 t 1 t 1 t 2 40; t 2 t 2 4 t 2 1 40; t 4 5t 2 36 0; 9 t 2 4 0; 3 t 3. 1 ,x 3 2. 3 2 1 1 1 Учитывая условия, получаем: 0 x , x 3 , 3 2 x 2, x 2 . 2 2 2 1 1 1 2; . Ответ: 0; ; ; 3 ; 3 2; 2 ; 2 2 2 Содержание критерия Баллы Обоснованно получен верный ответ 3 Обоснованно получен ответ, отличающийся от верного конечным количеством значений переменной, при которых определена левая 2 часть исходного неравенства Решение содержит верный переход от исходного неравенства к рациональным неравенствам или верно найдены все значения 1 переменной, при которых определена левая часть исходного неравенства Решение не соответствует ни одному из критериев, перечисленных 0 выше Максимальный балл 3 Значит, 3 log x 2 3 , откуда 0 x C4 Точки M , K и N лежат на сторонах соответственно AB , BC и AC треугольника ABC , причём AMKN — параллелограмм, площадь которого 4 составляет площади треугольника ABC . Найдите диагональ MN 9 параллелограмма, если известно, что AB 21 , AC 12 и BAC 120 . Решение. BK k . Тогда BC треугольник MBK подобен треугольнику ABC с коэффициентом k , а треугольник NKC — с коэффициентом 1 k . 4 2 2 S S AMKN SMBK S NKC ; S S k 2S 1 k S ; k 2 k 0 , 9 9 2 1 откуда получаем: k или k . 3 3 Пусть площадь треугольника ABC равна S, а A M N C K B Рис. 1 1 2 В первом случае (рис. 1): AM NK AB 7; AN MK AC 8. 3 3 Следовательно, MN AM 2 AN 2 2 AM AN cos120 13. A N M C Рис. 2 Во втором случае (рис. 2): AM NK K B 2 1 AB 14; AN MK AC 4. 3 3 Следовательно, MN AM 2 AN 2 2 AM AN cos120 2 67. Ответ: 13 или 2 67. Содержание критерия Баллы Обоснованно получен верный ответ 3 Рассмотрена хотя бы одна возможная геометрическая конфигурация, 2 для которой получено правильное значение искомой величины Рассмотрена хотя бы одна возможная геометрическая конфигурация, для которой получено значение искомой величины, неправильное из1 за арифметической ошибки Решение не соответствует ни одному из критериев, перечисленных 0 выше Максимальный балл 3 C5 Найдите все значения a , при каждом из которых система y 5 4 x x 2 2, y 9 a 2 2ax x 2 a имеет единственное решение. Решение. Система имеет единственное решение тогда и только тогда, когда графики функций y 5 4 x x 2 2 и единственную общую точку. Первое уравнение запишем в виде y a 4 a 2 2ax x 2 имеют y 2 9 ( x 2)2 , то есть ( y 2) 2 ( x 2) 2 9 при y 2 . Эти условия задают верхнюю полуокружность с центром (2; 2) и радиусом 3. Второе уравнение запишем в виде y a 9 ( x a)2 , то есть ( x a ) 2 ( y a ) 2 9 при y a . Эти условия задают верхнюю полуокружность с центром (a; a) и радиусом 3 . При a 2 полуокружности совпадают. При a 1,a 5 полуокружности не имеют общих точек. При 1 a 5,a 2 , они имеют единственную общую точку. Ответ: 1 a 2; 2 a 5. Содержание критерия Баллы Обоснованно получен верный ответ 4 С помощью верного рассуждения получены верные значения параметра, но – или ответ отличается от верного конечным числом значений 3 параметра; – или решение недостаточно обосновано С помощью верного рассуждения получен хотя бы один промежуток 2 значений параметра, одна из границ которого верная Задача сведена к исследованию: – или взаимного расположения двух полуокружностей; 1 – или квадратного уравнения с параметром Решение не соответствует ни одному из критериев, перечисленных 0 выше Максимальный балл C6 4 Можно ли привести пример пяти различных натуральных чисел, произведение которых равно 720, и а) пять; б) четыре; в) три из них образуют геометрическую прогрессию? Решение. а) Покажем, что пяти чисел, образующих геометрическую прогрессию быть не может. Действительно, пусть такие пять чисел найдутся. Обозначим первый член прогрессии b1 , а знаменатель прогрессии q . Тогда 5 720 b1 b1q b1q 2 b1q 3 b1q 4 b15q10 b1q 2 , то есть 720 является пятой степенью. Противоречие. б) Покажем, что четырёх чисел, образующих геометрическую прогрессию, быть не может. Пусть среди натуральных чисел, дающих в произведении 720, есть четыре целых числа, образующих геометрическую прогрессию. Обозначим первый член прогрессии b1 , а знаменатель m прогрессии q 1 m , n — взаимно простые числа, причём m 1 . Тогда n произведение этих четырёх чисел будет являться делителем числа 720. b 4m6 Заметим, что произведение чисел равно 1 6 . Так как числа m , n n взаимно просты, простые множители числа m будут входить в состав произведения чисел в той степени, в которой они входят в число b14 m 6 , то есть как минимум в шестой степени. Однако 720 24 32 5 , то есть простых множителей, входящих в шестой степени, в составе этого числа нет. в) Приведём пример пяти чисел, произведение которых равно 720 , среди которых есть три, образующих геометрическую прогрессию: 1, 2, 4, 6, 15. Ответ: а) нет; б) нет; в) да. Содержание критерия Баллы Верно выполнены: а), б), в) 4 Верно выполнены б) и один пункт из двух: а), в) 3 Верно выполнено б) или а) и в) 2 Верно выполнен один пункт из двух: а), в) 1 Решение не соответствует ни одному из критериев, перечисленных 0 выше Максимальный балл 4


