течение нелинейно-вязкой жидкости во вращающемся

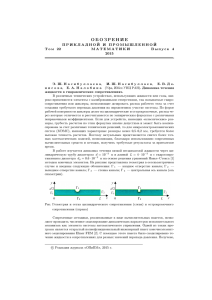
Течение нелинейно-вязкой жидкости во вращающемся вокруг вертикальной оси криволинейном
конвергентном канале
Г. В. Рябчук, д-р. техн. наук; Н. Л. Щербакова
ВолгГТУ, г. Волгоград
Течение жидкости во вращающихся вокруг вертикальной оси криволинейных конвергентных каналах
реализуется в центробежных насосах различной конструкции. Получение прогнозируемых напорнорасходных характеристик возможно на основе анализа полных уравнений движения с учетом
диссипативного разогрева среды и зависимости вязкости от температуры. Поэтому настоящая работа
является весьма актуальной и представляет значительный теоретический и прикладной интерес.
z
r0
h
0
r

R

Рисунок 1 - Схема конвергентного канала
Течение неньютоновской жидкости в конвергентном криволинейном канале рассмотрим в
цилиндрической системе координат r ,  , z (рис.1). Под действием давления «прокачки» или в результате
подсоса жидкости, вследствие ее сброса с периферии канала, среда поступает в начальное сечение канала
r  r0 . Жидкость прилипает к поверхности канала, т. е. радиальная компонента скорости на стенке равна
нулю, тангенсальная - r , а температура среды равна температуре стенки канала. Течение симметрично
относительно оси канала, следовательно, градиенты радиальной и тангенсальной компонент скорости,
градиенты давления и температуры равны нулю. Течение напорное, поэтому компонента осевой скорости на
оси r равна нулю.
В качестве реологической модели нелинейно-вязкой жидкости выберем «степенной» закон Оствальда де Виля
 ij  2k  ij  A n 1 ,
(1)
где  ij - тензор напряжений; ij - тензор скоростей деформации;
k - характеристика
консистентности среды; n - индекс течения; A - интенсивность скоростей деформации:
2r r 2  2r r 2  2r z2   r   r 2 
.
A
  r   r 2   r   z2   z 2


z
r

 







Уравнения в компонентах напряжения в выбранной системе координат запишутся в виде:


 r r r  z r z  2 r   P r   rr r   rr r   rz z    r ,
 r  r  z  z  r  r    r  r  2  r r   z z ,
(2)
 r z r  z z z   P z   rz r   zr r   zz z ,
здесь P - давление в жидкости и  - плотность среды.
Уравнение неразрывности принимает вид
r r  r r  z z  0 .
Уравнение теплопереноса
(3)


r T r  z T z  a  2T z2  1 r  r  T r  r  E ,
где E - энергия диссипации.
1  rr r r     r r    zz z z   r  r    r r 
E

,
c  rz z r  r  z   r  z

где c - удельная теплоемкость.


 
 
Компоненты тензора напряжения определяются из зависимости так:
(4)
(5)
 rr  2k  r r  A n 1 ,    2k  r r  A n 1 ,
 zz  2k  z z  A n 1 ,  r   k   r   r   A n 1 ,
(6)
 r  k   z   A ,  rz  k  z r  r z  A .
Как известно, для нелинейно-вязкой жидкости параметр переноса количества движения - эффективная
вязкость - зависит от интенсивности скоростей деформаций. В связи с этим предположим, что и параметр
процессов переноса тепла также зависит от интенсивности скоростей деформаций:
(7)
a*  a  n1  An1 ,
n 1
n 1

n1

n1
где a  a    A
- эффективный коэффициент температуропроводности среды; a - коэффициент
температуропроводности, определенный для линейной субстанции;   1  - характеристическое время; 
- угловая скорость вращения.
Используем в уравнении (4) эффективный аналог коэффициента температуропроводности
*


r T r  z T z  a*  2T z2  1 r  r  T r  r  k c  A n 1 .
(8)
Система уравнений должна решаться при следующих граничных условиях при z  0 :
r z   z  0; P z  0; z  0 , T z  0 ,
(9а)
(9б)
z  h ; r  z  ;   r ; T  Tст .
Зависимость характеристики консистентности среды от температуры представим в виде
k  k0  e T ,
где k0 - характеристика консистентности среды в начале участка течения в конвергентном канале (при
r  r0 );  - коэффициент, определяемый экспериментальным путем; T0 - температура среды на входе в
аппарат.
Решение системы уравнений (2, 3, 8) будем искать в виде, предложенном Г. В. Рябчуком:
 
 
r  U0  r0 r n 2 n  f   , P  P0    U02  r0 r 2n 2 n  F   ,
 
  U 0  r0 r n 2 n     , T  Tст  T0  Tст   r0 r n 2 n   J   ,
(10)
n 2  n 
z  U0  r0 r 
 G  , k  k0     ,
где
характерная
для
вращающихся
потоков
скорость;
U0  r0 P0 - задаваемое давление на конце канала;   z r - автомодельная переменная; f ,  , G , F , J ,  соответственно безразмерные радиальная, тангенциальная и осевая скорости, давление, температура и
характеристика консистентности:
r R n 2 n
  e * J , где  *    0 n 2  n .
r R 
В дальнейшем, полученная система интегрируется методом Рунге-Кутта четвертого порядка на
интервале  k ; 0 с реализацией процедуры редукции к задаче Коши методом Ньютона.
Параметрами интегрирования являются n ,  , модифицированный критерий Рейнольдса

2 n
 n 1r0
n
 r0 , модифицированный критерий Пекле Pe* 
.
n 2
k0
aU 0
Граничные условия преобразованы к следующему виду при
f      F   G  J '  0 ,
Re 
*
2
   k ; f   0 ,  к  
r R
r0 Rn 2n
  0;
(11а)
2 2 n
 0, J  0.
(11б)
Вид зависимости давления от радиуса определялся предварительно при рассмотрении течения при малых
значениях числа Рейнольдса. Закон изменений полувысоты канала от радиуса задавался в виде
2
r R
 .
 k i 1   k i  i
 r0 R 
Некоторые результаты численного интегрирования системы представлены на графиках (рис. 2, 3, 4, 5, 6)
при   0,01 , Re *  50 , Pe*  1000 , в сечении r R  1 , причем r0 R  0,1 . 1) n  1,1 ; 2) n  1,0 ;
3) n  0,9 ; 4) n  0,8 .
Рисунок 2 - Распределение безразмерной радиальной
скорости
Рисунок 3 - Распределение безразмерной
тангенциальной скорости
Рисунок 4 - Распределение безразмерного давления
Рисунок 5 - Распределение безразмерной осевой
скорости
По результатам численного интегрирования могут
быть определены основные гидродинамические
параметры процесса течения и
получены
напорно-расходные характеристики при различных
параметрах работы.
Рисунок 6 - Распределение безразмерной
температуры(аспирант каф. ПАХП Щербакова Н..Л.)