17) Задан закон распределения дискретной случайной
advertisement
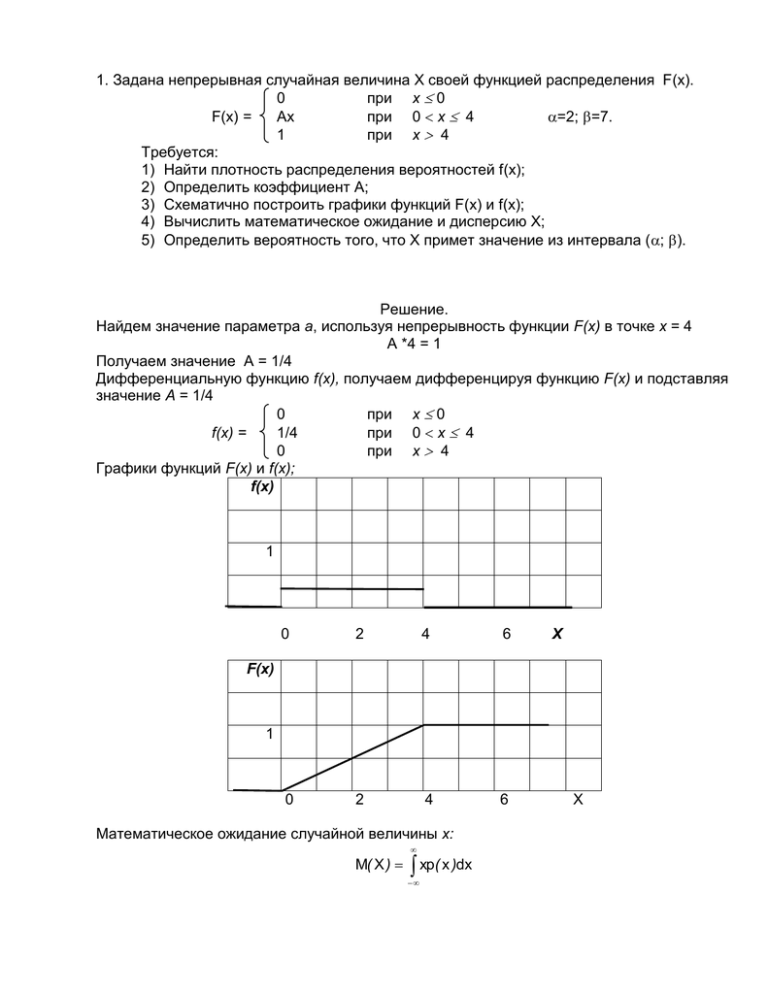
1. Задана непрерывная случайная величина Х своей функцией распределения F(x). 0 при x 0 F(x) = Ах при 0 x 4 =2; =7. 1 при x 4 Требуется: 1) Найти плотность распределения вероятностей f(x); 2) Определить коэффициент А; 3) Схематично построить графики функций F(x) и f(x); 4) Вычислить математическое ожидание и дисперсию Х; 5) Определить вероятность того, что Х примет значение из интервала (; ). Решение. Найдем значение параметра a, используя непрерывность функции F(x) в точке x = 4 А *4 = 1 Получаем значение А = 1/4 Дифференциальную функцию f(x), получаем дифференцируя функцию F(x) и подставляя значение А = 1/4 0 при x 0 f(x) = 1/4 при 0 x 4 0 при x 4 Графики функций F(x) и f(x); f(x) 1 0 2 4 6 0 2 4 6 X F(x) 1 Математическое ожидание случайной величины x: M( X ) xp( x )dx X 0 4 x * 0dx x * M( X ) 0 1 x2 dx x * 0dx 4 8 4 4 0 16 0 2 8 дисперсия случайной величины x: D( X ) [ X M( X )] 2 p( x )dx 0 D( X ) 4 2 2 x 2 * 0dx x 2 * 0 x 2 1 2 dx x 2 * 0dx 4 12 4 3 4 0 8 8 4 12 12 3 Определим вероятность того, что случайная величина x попадет в интервал (2; 7). P(x1 X x2) = F(x2 ) - F(x1 ) = F(7) - F(2) = 1 – 2/4 = 1/2 P(2 X 7) = 0,5 2. Случайная величина задана функцией распределения F(x). Найти а) плотность распределения случайной величины б) вероятность попадания случайной величины в интервал (a, b). Найти числовые характеристики. 0 при x < 0 2 F(x) = x при 0 x 1 1 при x 1 a) Плотность распределения вероятностей f(x), получаем дифференцируя функцию F(x) 0 при x < 0 f(x) = 2x при 0 x 1 0 при x 1 б) Определим вероятность того, что случайная величина x попадет в интервал (а; b). P(а X b) = F(b ) - F(а ) Математическое ожидание случайной величины х: M( X ) x f( x )dx 0 1 1 x3 M ( X ) x * 0dx x * 2 xdx x * 0dx 2 x dx 2 3 0 1 0 Дисперсия случайной величины x: D( X ) M( X 2 ) [ M( X )] 2 1 2 0 2 3 0 1 1 x4 M ( X ) x * 0dx x * 2 x dx x * 0dx 2 x dx 2 4 0 1 0 2 2 2 2 1 3 0 2 1 4 2 2 D( X ) M ( X 2 ) [ M ( X )] 2 1 2 1 4 98 1 2 3 2 9 18 18 3. Нормально распределенная случайная величина Х задана своими параметрами а (математическое ожидание) и (среднее квадратическое отклонение). Требуется: а) написать плотность вероятности и схематически изобразить ее график; б) определить вероятность того, что Х примет значение из интервала (;); в) определить вероятность того, что Х отклонится (по модулю) от а не более чем на . а=9; =3; =3; =12; =6. а) напишем плотность вероятности нормально распределенной случайной величины Х: 2 2 2 1 1 f x e x a / 2 e x 9 / 18 2 3 2 изобразим схематически график f(x) 9 х б) Вероятность того, что х примет значения, принадлежащее интервалу (3;12) составляет; 12 а 3 а 12 9 3 9 P3 x 12 Ф Ф Ф Ф Ф1 Ф 2 Ф1 Ф2 3 3 где Ф(х) – функция Лапласа. По таблице находим: P3 x 12 Ф1 Ф2 0,3413 0,4772 0,8185 в) Вероятность того, что абсолютная величина отклонения Ix-аI окажется меньше =6 6 P x а 2Ф 2Ф 2Ф2 2 * 0,4772 0,9544 3 4. Непрерывная случайная величина задана интегральной функцией F(x). 0 при x 3 F(x) = a (x - 3) при 3 x 8 1 при x 8 Требуется найти: а) значение параметра а; б) дифференциальную функцию f(x); в) математическое ожидание и дисперсию случайной величины x; г) построить график функций F(x) и f(x); д) вероятность того, что случайная величина x попадет в интервал (-1; 4). Решение. а) Найдем значение параметра a, используя непрерывность функции F(x) в точке x = 8 а *(8 - 3) = 1 Получаем значение а = 1/5 б) Дифференциальную функцию f(x), получаем дифференцируя функцию F(x) и подставляя значение а = 1/5 0 при x 3 p(x) = 1/5 при 3 x 8 0 при x 8 в) математическое ожидание случайной величины x: M( X ) xp( x )dx 3 M( X ) 8 x * 0dx x * 3 1 x2 dx x * 0dx 5 10 8 8 5,5 3 дисперсия случайной величины x: D( X ) [ X M ( X )] 2 p( x )dx 3 D( X ) 8 2 2 [ x 5,5 ] * 0dx [ x 5,5 ] * 3 г) графики функций F(x) и p(x); 1 [ x 5,5 ] 3 dx [ x 5,5 ] 2 * 0dx 5 15 8 8 3 25 2,08 12 f(x) 1 1/5 0 2 4 6 8 10 X 2 4 6 8 10 X F(x) 1 0 д) Определим вероятность того, что случайная величина x попадет в интервал (-1; 4). P(x1 X x2) = F(x2 ) - F(x1 ) = F(4) - F(-1) = 1/5 – 0 = 1/5 P(x1 X x2) = 0,2 5. . Функция распределения F(x) непрерывной случайной величины Х имеет вид: F(x) = 0 А+Вcosx 1 x /2 /2 x x Найти: неизвестный коэффициент А; функцию плотности распределения f(x); математическое ожидание М[X], дисперсию D[X]; вероятность попадания Х в интервал Р(0<X<2/3); построить графики функций f (x), F (x). Решение. Найдем значение параметров А и В, используя непрерывность функции F(x) сначала в точке x=/2, используя первое и второе условия в описании функции F(x) F(/2) =0 F(/2) = А+Вcos(/2)=А А=0 Теперь используем непрерывность функции F(x) в точке x=, используя второе и третье условия в описании функции F(x) F() = Вcos= -В F() = 1 В= -1 Функция распределения F(x) непрерывной случайной величины Х имеет вид: x /2 /2 x x 0 -cosx 1 F(x) = Функцию плотности распределения f(x), получаем дифференцируя функцию F(x) x /2 /2 x x 0 sinx 0 f(x) = Математическое ожидание случайной величины x: M( X ) xf ( x )dx M( X ) π/2 π π π/2 π π/2 x * 0dx π x sin x x * 0dx π x cos x π / 2 cos xdx π 0 sin x x sin xdx π π/2 ux dv sin xdx du dx v cos x π 0 1 π 1 π/2 дисперсия случайной величины x: D X M X 2 M ( X ) π x M X2 π/2 2 sin xdx 2 π π u x2 dv sin xdx x 2 cos x 2 x cos xdx π/2 du 2 xdx v cos x π/2 π u 2x dv cos xdx π π π 2 π 0 2 x sin x π / 2 2 sin xdx π 2 0 2 2 cos x π / 2 du 2dx v sin x 2 π/2 π 2 π 2 0 π 2 π 2 2 2 D X M X 2 M ( X ) π 2 π 2 π 1 π 3 Определим вероятность попадания Х в интервал Р(0<X<2/3) P(x1 X x2) = F(x2 ) - F(x1 ) = F(2/3) - F(0) = -cos(2/3) – 0 = 1/2 P(x1 X x2) = 0,5 Построим графики функций F(x) и p(x); f(x) 1 0 1 2 3 4 1 2 3 4 X F(x) 1 0 5 X
