Тема 1. Представление исходных данных МЕЖДУНАРОДНЫЙ БАНКОВСКИЙ ИНСТИТУТ INTERNATIONAL BANKING INSTITUTE
advertisement
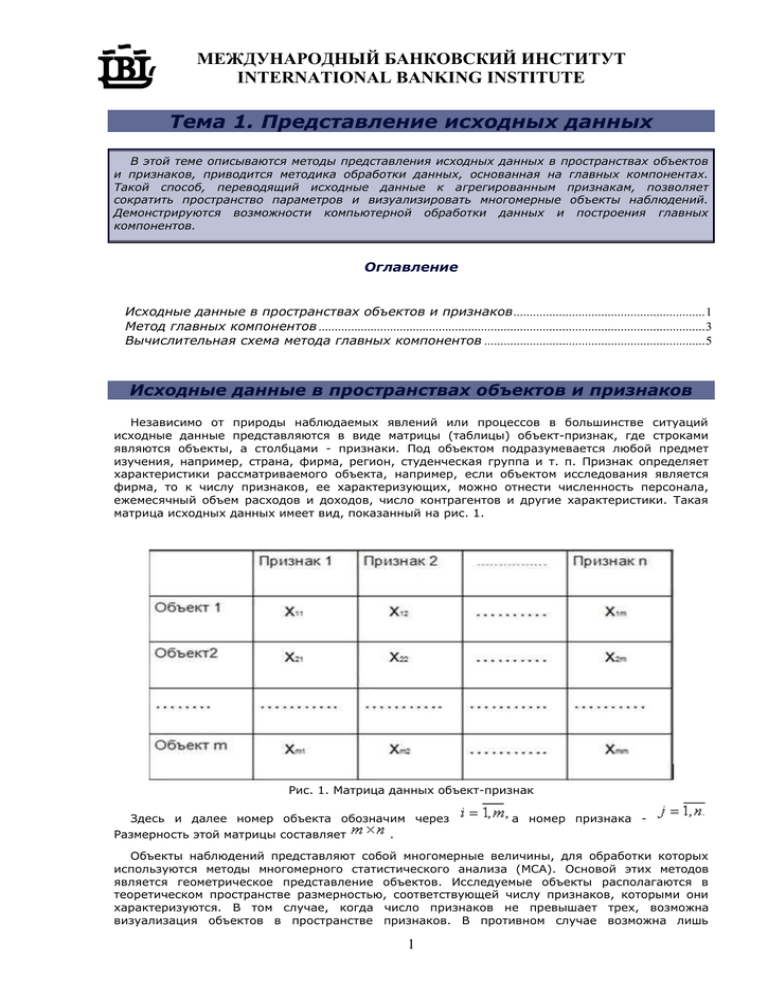
МЕЖДУНАРОДНЫЙ БАНКОВСКИЙ ИНСТИТУТ INTERNATIONAL BANKING INSTITUTE Тема 1. Представление исходных данных В этой теме описываются методы представления исходных данных в пространствах объектов и признаков, приводится методика обработки данных, основанная на главных компонентах. Такой способ, переводящий исходные данные к агрегированным признакам, позволяет сократить пространство параметров и визуализировать многомерные объекты наблюдений. Демонстрируются возможности компьютерной обработки данных и построения главных компонентов. Оглавление Исходные данные в пространствах объектов и признаков ........................................................... 1 Метод главных компонентов ....................................................................................................................... 3 Вычислительная схема метода главных компонентов .................................................................... 5 Исходные данные в пространствах объектов и признаков Независимо от природы наблюдаемых явлений или процессов в большинстве ситуаций исходные данные представляются в виде матрицы (таблицы) объект-признак, где строками являются объекты, а столбцами - признаки. Под объектом подразумевается любой предмет изучения, например, страна, фирма, регион, студенческая группа и т. п. Признак определяет характеристики рассматриваемого объекта, например, если объектом исследования является фирма, то к числу признаков, ее характеризующих, можно отнести численность персонала, ежемесячный объем расходов и доходов, число контрагентов и другие характеристики. Такая матрица исходных данных имеет вид, показанный на рис. 1. Рис. 1. Матрица данных объект-признак Здесь и далее номер объекта обозначим через Размерность этой матрицы составляет а номер признака - . Объекты наблюдений представляют собой многомерные величины, для обработки которых используются методы многомерного статистического анализа (МСА). Основой этих методов является геометрическое представление объектов. Исследуемые объекты располагаются в теоретическом пространстве размерностью, соответствующей числу признаков, которыми они характеризуются. В том случае, когда число признаков не превышает трех, возможна визуализация объектов в пространстве признаков. В противном случае возможна лишь 1 МЕЖДУНАРОДНЫЙ БАНКОВСКИЙ ИНСТИТУТ INTERNATIONAL BANKING INSTITUTE математическая идеализация представления объектов в многомерном пространстве, либо необходим переход к некоторым агрегированным признакам, позволяющим снизить размерность наблюдений. В многомерном пространстве признаки или объекты имеют определенные количественные характеристики. Все принимаемые значения признаков (объектов) представляют собой множества вещественных чисел. При использовании методов МСА необходимо принимать во внимание следующие особенности: в m-мерном пространстве сохраняют силу принципиальные положения и аксиомы евклидовой геометрии; в МСА, как правило, используется большое число признаков, разнородных по своей природе. В связи с этим на первом этапе исследования обычно возникает проблема приведения всех признаков к одному основанию: сопоставимому виду. Подобные проблемы решаются нормированием данных, что геометрически означает изменение масштаба, и другими преобразованиями координатной системы. обработка m-мерных совокупностей включает большое число сложных и трудоемких арифметических операций, поэтому осуществляется на основе пошаговых алгоритмов. При обработке многомерных данных следует учитывать дуализм представления, так как имеются возможности визуализации как объектов в пространстве признаков, так и признаков в пространстве объектов. Кроме представления исходных данных в виде матрицы объект-признак, имеются и другие возможности представления. Например, с помощью коэффициента корреляции между признаками, который вычисляется по формуле где - среднее значение произведения величин признаков x i, xk; , ( - среднее значение признака xi, (xk); si(sk) - среднеквадратичное отклонение соответствующих признаков, можно представить исходные данные в виде матрицы признак-признак (рис. 2). Рис. 2. Матрица признак-признак Эта матрица в отличие от предыдущей имеет размерность . В каждой ячейке матрицы расположены значения коэффициента корреляции между соответствующими признаками; на диагонали матрицы стоят единицы, так как корреляция признака с самим собой максимальна и равна единице. Матрица симметрична относительно своей диагонали. Такая матрица применяется при вычислении главных компонентов. 2 МЕЖДУНАРОДНЫЙ БАНКОВСКИЙ ИНСТИТУТ INTERNATIONAL BANKING INSTITUTE Сходство или различие между классифицируемыми объектами устанавливается в зависимости от метрического расстояния между ними. Если каждый объект описывается n признаками, то он может быть представлен как точка в n -мерном пространстве, и его сходство с другими объектами будет определяться как соответствующее расстояние. Указанное обстоятельство позволяет перейти к еще одному виду представления исходных данных, а именно, к матрице объект-объект, представляющей собой таблицу расстояний между анализируемыми объектами. В этом случае в каждой ячейке матрицы находится величина расстояния, допустим, евклидова, рассчитываемого по формуле . Здесь xij, xkj- значения j-го признака, соответственно, у i-го и k-го объектов. Такая матрица, размерностью , имеет вид, показанный на рис. 3. Рис. 3. Матрица объект-объект На диагонали матрицы находятся нули, поскольку расстояние от точки до нее самой равно нулю. Элементы матрицы симметричны относительно диагонали. Таким образом, исходные данные могут быть представлены в виде матриц трех типов: матрицы объект-признак; матрицы признак-признак; матрицы объект-объект. Метод главных компонентов Любое исследование многомерных данных невозможно без использования метода главных компонентов (ГК). Сущность этого метода заключается в снижении размерности данных путем определения незначительного числа линейных комбинаций исходных признаков, которые объясняют большую часть изменчивости данных в целом. Метод ГК связан с переходом к новой системе координат, которая является системой ортонормированных линейных комбинаций. Этот метод дает возможность по n исходным признакам объектов построить такое же количество ГК, являющихся обобщенными (агрегированными) признаками. На первый взгляд, такой переход не дает никакого преимущества в представлении данных, но существует возможность сохранения информации о рассматриваемых данных даже в том случае, если сократить количество вычисленных ГК. Кроме того, при сохранении двух или трех ГК реализуется возможность визуализации многомерных объектов в сокращенном признаковом пространстве. Метод ГК обладает рядом свойств, делающим его эффективным для визуализации структуры многомерных данных. Все они касаются наименьшего искажения геометрической структуры точек (объектов) при их проектировании в пространстве меньшей размерности. 3 МЕЖДУНАРОДНЫЙ БАНКОВСКИЙ ИНСТИТУТ INTERNATIONAL BANKING INSTITUTE Математическая модель ГК базируется на допущении, что значения множества взаимосвязанных признаков порождают некоторый общий результат. В этой связи при представлении исходных данных, о чем говорилось в предыдущем параграфе, как раз и важна матрица признак-признак, в которой содержится вся информация о попарной связи между признаками. Предположив линейную форму связи между признаками, можно записать в матричной форме уравнение зависимости результата F от признаков Х в виде где В - вектор параметрических значений линейного уравнения связи. Условием выполнения такого равенства является соответствие дисперсий, т. е. D (X)=D (XB). Поскольку Х является многомерной случайной величиной, то ее дисперсионная оценка - это ковариационная матрица S. Постоянная величина В выносится за знак дисперсии и возводится в квадрат, в результате чего получаем D (F)= B ' SB. Первым ГК f1(х) набора первичных признаков Х=(х1,х2,…,хn) называется такая линейная комбинация этих признаков, которая среди прочих линейных комбинаций обладает наибольшей дисперсией. Геометрически это означает, что первый ГК ориентирован вдоль направления наибольшей вытянутости гиперэллипсоида рассеивания исследуемой совокупности данных. Второй ГК имеет наибольшую дисперсию рассеивания среди всех линейных преобразований, некоррелированных с первым ГК, и представляет собой проекцию на направление наибольшей вытянутости наблюдений в гиперплоскости, перпендикулярной первому ГК. Вообще, j–м ГК системы исходных признаков Х=(х1, х2,…,хn) называется такая линейная комбинация этих признаков, которая некоррелирована с (j-1) предыдущими ГК и среди всех прочих некоррелированных с предыдущими (j-1) ГК обладает наибольшей дисперсией. Отсюда следует, что ГК занумерованы в порядке убывания их дисперсий, т.е. , а это дает основу для принятия решения о том, сколько последних ГК можно без ущерба изъять из рассмотрения. Поиск ГК сводится к задаче последовательного выделения первого ГК с наибольшей дисперсией, второго ГК и т. д. Подобная задача имеет место при условии введения ограничений. Пусть При чего получим максимизируем , используя метод множителей Лагранжа, в результате откуда С учетом последнего равенства для характеристического уравнения, позволяющего найти значения j, имеем где Е - единичная матрица. Из множества значений характеристических (собственных) чисел j определяем наибольшее 1 и находим соответствующий собственный вектор В1, который используется при вычислении первого ГК. Для вычисления второго ГК определяются следующее по величине собственное число 2 и собственный вектор В2 и т.д. Если исходную матрицу данных Х предварительно стандартизировать, то матрица ковариаций S перейдет в матрицу парных корреляций R, и вектор B будет собственным 4 МЕЖДУНАРОДНЫЙ БАНКОВСКИЙ ИНСТИТУТ INTERNATIONAL BANKING INSTITUTE вектором по стандартизованным данным U. Решающее уравнение в матричной форме принимает вид Полученное уравнение называется характеристическим для матрицы R и представляет собой алгебраическое уравнение n-й степени относительно переменной l. Окончательно, соотношения для определения всех n ГК исходного n-мерного вектора Х могут быть представлены в виде F = B Х. Отметим основные свойства ГК: математическое ожидание ГК равно нулю; ГК некоррелированы между собой; сумма дисперсий исходных признаков равна сумме дисперсий всех ГК; значимость каждого ГК убывает с его номером и определяется соответствующим собственным числом. Учитывая указанные свойства, можно предложить критерий для определения количества ГК, которые полезно оставить в качестве агрегированных признаков. Этот критерий может быть записан в виде где n* - число оставленных в наборе агрегированных признаков. Этот критерий достигает максимума, равного единице, только при n*= n. Вычислительная схема метода главных компонентов Решение задачи методом ГК сводится к поэтапному преобразованию матрицы исходных данных. Основные шаги метода показаны на схеме, приведенной на рис. 4. Рис. 4. Вычислительная схема метода главных компонентов 5 МЕЖДУНАРОДНЫЙ БАНКОВСКИЙ ИНСТИТУТ INTERNATIONAL BANKING INSTITUTE Прокомментируем этапы вычислений. В качестве исходных данных обычно выбирается матрица объект-признак Х. Поскольку характеристиками объектов могут служить признаки различной природы, то данные необходимо стандартизировать, т.е. провести центрирование (вычитание среднего значения) и нормирование (деление на среднеквадратичное значение) данных. На следующем шаге вычисляется матрица корреляций R между признаками, т.е. осуществляется переход к матрице признак-признак. Диагональные элементы этой матрицы равны единице, а сама матрица симметрична относительно этой диагонали, так как rij= rji. Далее определяется матрица собственных векторов В, которая, также, как и предыдущая, является квадратной и состоит из n строк и n столбцов. Компоненты каждого собственного вектора представлены в виде вектора-столбца, сумма квадратов составляющих которого вследствие ортогональности равна единице. На следующем этапе проводится расчет матрицы собственных чисел , которая в отличие от предыдущих матриц является диагональной, т.е. здесь только на диагонали матрицы находятся собственные числа: все прочие элементы матрицы равны нулю. Размерность этой матрицы, как и двух предыдущих, составляет Суммарное значение . Каждое значение j определяет дисперсию каждого ГК. равняется сумме дисперсий исходных признаков. При условии стандартизации исходных данных На последнем шаге вычисляются ГК: с помощью матрицы находятся два или три наибольших собственных числа (такой выбор обусловлен желанием визуализировать многомерные объекты в двумерной плоскости или трехмерном пространстве); по матрице В определяются собственные вектора, которые соответствуют выбранным собственным числам; найденные таким образом собственные вектора умножаются последовательно на строки исходной матрицы, формируя значения ГК для каждого объекта. Например, при выборе только первых двух наибольших собственных чисел определяем соответствующие им составляющие собственных векторов (два столбца матрицы В), которые перемножаем на строки матрицы Х. Перемножение первого столбца матрицы В на первую строку матрицы Х даст значение первого ГК для первого объекта, умножение того же столбца на вторую строку определяет значение первого ГК для второго объекта и т.д. После выполнения таких же операций со вторым выбранным вектором получаем возможность построить все объекты в плоскости первых двух ГК, где их взаимное расположение позволяет сделать предварительные выводы о сходстве (различии) объектов. Проведение вычислений ГК по приведенной схеме возможно лишь на компьютере, на котором установлен подходящий пакет программного обеспечения из области многомерной статистики. Хотя в литературе и указываются вычислительные методы (в частности, метод Фаддеева), позволяющие определить ГК с помощью калькулятора [1,2], на самом деле такой прием возможен лишь в ситуации, когда число признаков не превышает трех. В реальной ситуации число признаков может достигать намного больших значений, поэтому необходима помощь ПК. Из опыта работы автора наиболее приемлемыми пакетами для расчета ГК могут служить пакеты Statgraphics и Statistica, причем в силу большей простоты предпочтение следует отдать первому. В качестве примера на рис. 5 показан график, где в плоскости первых двух ГК представлена совокупность из 10 объектов, каждый из которых первоначально характеризуется 5 признаками. 6 МЕЖДУНАРОДНЫЙ БАНКОВСКИЙ ИНСТИТУТ INTERNATIONAL BANKING INSTITUTE Рис. 5. Объекты в плоскости первых двух ГК Как видно из графика, можно получить некоторые выводы о сходстве (различии) объектов при переходе к сокращенному двумерному пространству. Например, достаточно четко прослеживается деление объектов на две группы (объекты с номерами 1-5 и 6-10) и значительное рассеяние внутри этих групп. Таким образом, от пятимерного признакового пространства с помощью ГК осуществлен переход к двумерному пространству агрегированных признаков и визуализация многомерных объектов. 7
