Кургузов В.Д., Корнев В.М. ЗОНЫ ПРЕДРАЗРУШЕНИЯ В КВАЗИХРУПКИХ МАТЕРИАЛАХ

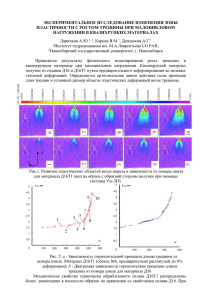
ЗОНЫ ПРЕДРАЗРУШЕНИЯ В КВАЗИХРУПКИХ МАТЕРИАЛАХ
ПРИ ВЕТВЛЕНИИ И ИЗЛОМЕ ТРЕЩИН
Кургузов В.Д., Корнев В.М.
Институт гидродинамики им. М. А. Лаврентьева СО РАН, Новосибирск, Россия
Рассматриваются тела с регулярной структурой. Предлагается строить решение нелинейной задачи механики разрушения в два этапа, когда для исходной трещины нормального отрыва возможно ветвление или излом. Сначала отыскиваются углы излома или ветвления трещины, а затем определяются критические параметры разрушения для выбранных направлений. На этих
этапах соответственно используются необходимый и достаточный критерии разрушения типа
Нейбера-Новожилова. При отыскании критических параметров разрушения (длин зон предразрушения и нагрузки) используется модификация классической модели Леонова-ПанасюкаДагдейла, когда зоны предразрушения занимают прямоугольники, расположенные вдоль отростков трещины. При построении простых выражений для критических параметров разрушения используются коэффициенты интенсивности напряжений для трещины с бесконечно малыми отростками и коэффициенты интенсивности напряжений для трещины с отростком, когда на
отростке заданы нормальные и сдвигающие напряжения, моделирующие зону пластичности.
Чтобы построить коэффициенты интенсивности напряжений для трещины с отростками, методом конечных элементов решена задача об одноосном растяжении пластины с трещиной, имеющей двоякосимметричное ответвление. Получены коэффициенты интенсивности напряжений
по 1-ой и 2-ой моде в зависимости от угла ветвления.
Введение
Вопросы устойчивого роста острых трещин (или их ветвления) при некотором
нагружении тела с прямолинейной острой трещиной представляют несомненный интерес.
В окрестности вершины острой трещины нормального отрыва возникает сложное поле
напряжений. При определенных условиях может происходить затупление острых трещин
из-за больших сдвиговых напряжений или деформаций. В работе [1] обнаружена возможность множественного ветвления трещин, что связывается с кратностью собственных значений при потере устойчивости системы, подчеркнем, что в этой работе [1] нагружение
соответствует первой моде разрушения. Получены соотношения, описывающие угол излома траектории трещины, когда известны кривые теоретической прочности типа КулонаМора. Трещина развивается по направлениям: 1) перпендикулярно направлению максимального растяжения при отсутствии сдвигающих напряжений в окрестности ее вершины
(гипотеза Эрдогана-Си), когда материал разрушается хрупко; 2) вдоль направления максимального сдвига при отсутствии нормальных напряжений в окрестности ее вершины,
когда материал разрушается вязко (имеет место испускание дислокации); 3) вдоль некоторого направления, соответствующего обобщенному напряженному состоянию, когда материал разрушается квазихрупко или квазивязко.
На рис. 1 приведена фотография из статьи [2], демонстрирующая асимметричное
формирование зон предразрушения в алюминиевой пластине с трещиной. Такая картина
наблюдается в тонких пластинах при полномасштабной пластическом течении в окрестности вершин трещин. Последующее распространение трещин происходит вдоль средней
линии зоны шейкообразования.
Ветвление и излом траектории острых трещин происходит, когда вершина плоской
трещины упирается в плоскую границу раздела монокристаллов. Эта граница раздела
(например, малоугловая граница) в структурированном материале рассматривается как
некоторое тонкое твердое тело регулярного строения с заданными свойствами. Если тонкое твердое тело имеет пониженные характеристики прочности по сравнению с идеальными монокристаллами, то предпочтительное распространение трещины совпадает с границей раздела монокристаллов [1].
Рис. 1. Асимметричное формирование зон предразрушения в алюминиевой пластине с
трещиной
1. Описание характеристик квазихрупкого материала со структурой при однократном нагружении
Рассмотрим внутреннюю прямолинейную острую трещину в структурнонеоднородном материале на 2-ом структурном уровне (зернистый материал). В изотропном упругом материале внутренняя трещина моделируется двусторонним разрезом длиной 2l . Пусть на бесконечности заданы нормальные   и касательные   напряжения,
т.е. трещина деформируется по смешанной моде (нормальный отрыв+сдвиг). При выходе
трещины на границу двух зерен возможно ветвление трещины или излом ее траектории
как следствие несимметрии прочностных свойств материала относительно плоскости
трещины. Введем полярную систему координат Or с полюсом O в правой вершине
трещины, направив полярную ось вдоль оси трещины. Обозначим через   углы ветвления (излома) трещины. При    0 трещина распространяется устойчиво, оставаясь прямолинейной; при    0 имеет место излом траектории трещины; при    0 трещина
ветвится, меняя свое направление, причем при     / 2 происходит затупление трещины при ее раскрытии [1]. По характеру поведения при разрушении материалы можно разделить на хрупкие (    0 ) и вязкие (     / 2 ), но возможно и квазихрупкое
(    0 ,    0 ) или квазивязкое (     / 2 ,     / 2 ) поведение.
При постепенном нагружении образца нагрузками   и   , приложенными на бесконечности, в окрестности вершины трещины реализуется сложное напряженное состояние. Будем рассматривать пропорциональное нагружение, когда   /    c  const . Выбор
того или иного пути ветвления и излома траектории трещины определяется прочностными
характеристиками материала. На рис. 2 приведены кривые теоретической прочности типа
Кулона-Мора для двух изотропных материалов. Кривая 1 описывает поведение квазивязкого материала, а кривая 2 – квазихрупкого материала. Пропорциональный путь нагружения (  /   c  const ) показан лучом 3, направление которого определяется углом  на
плоскости   , где  и  – нормальные и сдвигающие напряжения. Таким образом,
кривые 1, 2 в полярной системе координат могут быть записаны в виде fi  fi ( ) ( i  1, 2);
для изотропного материала имеем fi ( )  fi ( ) из-за выполнения условий симметрии.
Теоретические (идеальные) прочности материалов на растяжение обозначены  m1 ,  m 2
для кривых 1, 2 соответственно ( fi (0)   mi ). Теоретические (идеальные) прочности материалов на сдвиг обозначены  m1 ,  m 2 для кривых 1, 2 соответственно ( fi ( / 2)   mi ). Через
 * ,  * обозначены критические значения напряжений на заданном пути деформирования.
Ниже величины со звездочкой означают критическое состояние.
Рис. 2. Кривые теоретической прочности типа Кулона-Мора для двух изотропных материалов: 1 – квазивязкий материал, 2 – квазихрупкий материал, 3 – пропорциональный путь
нагружения
Относительные оценки теоретических прочностей на растяжение  m и сдвиг  m в
предельных случаях таковы: 1) для материалов, склонных к раскалыванию (хрупкий и
квазихрупкий материалы), имеем  m  m (кривая 2); 2. для материалов, слабо сопротивляющихся испусканию дислокаций (квазивязкий материал), имеем  m  m (кривая 1).
Для пропорционального пути нагружения рассмотрим    диаграммы деформирования материалов, где    2   2 – интенсивность напряжений,    2   2 – интенсивность деформаций. Диаграммы деформирования    могут быть получены,
например, в экспериментах на совместное растяжение и кручение тонкостенных трубчатых образцов [3]. На рис. 3 приведена простейшая аппроксимация реальной диаграммы
   деформирования квазихрупкого материала. Здесь  * – критические значения
напряжений;  0 – предельные деформации в зоне упругого деформирования;  * – деформации, соответствующие началу процесса разрушения.
Рис. 3. Простейшая аппроксимация диаграммы    деформирования квазихрупкого материала
2. Углы ветвления трещины (необходимый критерий разрушения)
Предположим, что исходная макротрещина является острой, а ее правая вершина
находится на границе двух зерен. Предположим, что материал является изотропным.
Рассмотрим силовой дискретно-интегральный критерий хрупкого разрушения типа
Нейбера–Новожилова [4, 5] подрастания трещин по выбранным направлениям  , определяемым углами ветвления,
r
r
1 0
1 0
*
(1)
  ( )     (r )dr     r ( )    r (r )dr   *.
r0 0
r0 0
Здесь Or – полярная система координат, когда начало отсчета совпадает с вершиной реальной трещины;   (r  ) и  r (r   ) – нормальные и касательные напряжения,
имеющие интегрируемую особенность;   ( ) ,  r ( ) – осредненные нормальные и касательные напряжения на выбранных направлениях  ; обозначения  *  f ( ) cos  ,
 *  f ( )sin  используются для напряжений критических состояний (рис. 2); r0 – характерный линейный размер структуры материала (диаметр зерна). Подчеркнем, что левые
части первого и второго соотношений (1) суть функции угла  , а правые части тех же соотношений суть функции угла  . Для трещин по I моде соотношение между этими углами было установлено ранее:    / 2 [1].
При  ( )    ,  r ( )    трещина не продвигается. Когда осредненные
напряжения   ( ) ,  r ( ) совпадают с напряжениями критических состояний   ,   ,
т.е.  ( )    и  r ( )    , выполняется критерий (1) на выбранных направлениях
  и начинается: 1) формирование единственной зоны предразрушения на продолжении
трещины, если    0 , 2) формирование двух зон предразрушения при ветвлении внутренней трещины длиной 2l , если    0 . Первый случай соответствует хрупкому и квазихрупкому разрушению, когда    0 . Второй случай соответствует квазивязкому разрушению, когда    / 2 .
Углы ветвления   определяются из следующего соотношения [1]
l (  )  min l ( ) .
Это соотношение описывает как простое, так и кратное ветвления трещин. Например, для
трехкратного ветвления имеем l1 (1 )  l2 (1 )  l3 (3 ) при 1  0, 3  0 . Подобное поведение системы было обнаружено в экспериментах [2]: для левой вершины трещины на
рис. 1 имеем    0 , а для правой вершины трещины на рис. 1 имеем    0 . Реализация
того или иного направления при распространении трещин в конкретных экспериментах
[2] зависит от незначительных возмущений в структуре материала в окрестности вершины
трещины.
Таким образом, необходимый критерий (1) описывает начало формирования единственной зоны предразрушения в первом материале или двух зон предразрушения во втором материале и позволяет определить углы   ветвления внутренней трещины. Этот необходимый критерий (4) не может описать длины зон предразрушения.
Для необходимого критерия соответствующие осредненные напряжения не превосходят теоретических прочностей на разрыв или сдвиг. При выполнении необходимого
критерия ближайшая к вершине структура материала находится в критическом состоянии.
Однако после исчерпания несущей способности ближайшей к вершине структуры возможно дополнительное догружение тела с трещиной за счет закритического деформирования этой структуры и докритического деформирования следующей структуры, когда в
окрестности вершины трещины отсутствуют повреждения. При выполнении достаточного
критерия имеет место катастрофическое разрушение исходной системы.
3. Достаточный критерий разрушения при обобщенном напряженном состоянии
Для описания напряженно-деформированного состоянии в окрестности вершины
трещины воспользуемся моделью Леонова–Панасюка–Дагдейла [6, 7]. Введем декартову
прямоугольную систему координат Oxy с началом в вершине трещины, ось Ox направим
вдоль оси трещины. Если в континуальной модели воспользоваться представлениями решений для напряжений на продолжении острой трещины y  0 через коэффициенты интенсивности напряжений K I , K II то с точностью до величин высшего порядка малости в
окрестности вершины трещины для линейной задачи можно записать
KI
KII
(2)
 y ( x 0) 
   ,  xy ( x 0) 
  ,
2 x
2 x
где   ,   – характерные напряжения, заданные на бесконечности, либо на контуре ограниченного тела; K I , K II — суммарные коэффициенты интенсивности напряжений (КИН).
Суммарные КИНы можно представить в виде
K I  K I  K I  K I  0 K I  0 , K II  K II  K II  K II  0 K II  0 .
(3)
Здесь K I , K II – КИНы, порождаемые напряжениями   ,   ; K I , K II – КИНы, порождаемые напряжениями  * ,  * , действующими в окрестности носика фиктивной трещины
в зоне предразрушения.
В классической модели Леонова–Панасюка–Дагдейла исходная внутренняя прямолинейная трещина длиной 2l0 подменяется фиктивной трещиной–разрезом длиной
2l  2l0  2 , где  – длина нагруженного участка или длина зоны предразрушения, две
зоны предразрушения расположены на продолжении исходной трещины. Схема силового
нагружения правого носика фиктивной трещины в обобщенной модели Леонова–
Панасюка–Дагдейла представлена на рис. 4, а (хрупкий материал, трещина распространяется прямолинейно) и на рис. 4, б (квазихрупкий материал, излом траектории трещины). В
классической модели в зоне предразрушения действуют только нормальные напряжения
 * , сдвигающие напряжения   и  * отсутствуют. Напряжения  * ,  * совпадают с
напряжениями критических состояний (см. рис. 2). Суммарный КИН K I не может быть
отрицательным, так как при K I  0 берега трещины налагаются друг на друга, что физически не реально.
Рис. 4. Схема силового нагружения правого носика фиктивной трещины в обобщенной
модели Леонова–Панасюка–Дагдейла
Для описания процесса разрушения в зоне предразрушения ветвящейся трещины
воспользуемся достаточным критерием разрушения [8, 9]. Поместим начало декартовой
прямоугольной системы координат Oxy в правую вершину отростка трещины, а ось Ox
направим вдоль отростка (рис. 4, б.), отросток трещины расположен под углом   к плоскости основной трещины. Таким образом, всю длину отростка занимает зона предразрушения; введем обозначения  для длины зоны предразрушения и a для поперечника этой
зоны. Достаточный дискретно-интегральный критерий квазихрупкой прочности для
острой трещины имеет вид:
r
r
1 0
1 0

(4)
 y ( x 0)dx   
 xy ( x 0)dx     x  0 ;


r0 0
r0 0

 1

(5)
 2v  , 2u () 
K II
 2u  ,    x  0 .
G
2
G
2
Здесь  y ( x 0) и  xy ( x 0) – нормальные и касательные напряжения на продолжении от2v () 
 1
KI
ростка трещины, имеющие интегрируемую особенность; r0 – интервал осреднения;
2v  2v ( x) и 2u  2u ( x ) – раскрытие отростка трещины и смещение берегов отростка
трещины соответственно; 2v  и 2u  – критическое раскрытие отростка трещины и критическое смещение берегов отростка трещины соответственно;   3  4 для плоской деформации,   (3  ) /(1  ) для плоского напряженоого состояния, где  – коэффициент
Пуассона; G – модуль сдвига; K I и K II – суммарные коэффициенты интенсивности
напряжений в обобщенной модели Леонова-Панасюка-Дагдейла.
Длина зоны предразрушения  определяется при решении задачи о разрушении
(4), (5), а поперечник этой зоны a отыскивается из решения упругопластической задачи
[10]. На рис. 5 заштрихована пластическая зона в окрестности правой вершины трещины,
диаметр пластической зоны равен a . Приравниваем площадь пластической зоны площади
прямоугольника со сторонами a и  , показанного на рис. 5. Таким образом, пластическая
зона в окрестности вершины трещины аппроксимируется прямоугольной зоной предразрушения с поперечником a и длиной  . Критические параметры 2v  и 2u  находятся из
соотношений
2v   a* ( *   0 ), 2u   a* ( *   0 ) ,
(6)
где  0  ( 0 )2  ( 0 )2 ,  *  ( * ) 2  ( * ) 2 определяются по диаграмме    (рис. 3).
Рис. 5. Аппроксимация пластической зоны в окрестности вершины трещины зоной
предразрушения
Система из первых соотношений критерия (4), (5) эквивалентна системе из вторых
соотношений критерия (4), (5), если имеет место пропорциональное нагружение, а тензоры напряжений и деформаций соосны [8, 9]. В отличие от классических критериев разрушения [6, 7, 11], в критерии (4), (5) используются ограничения
(7)
K I  0 , K II  0 ,
а поперечник зоны предразрушения отождествляется с поперечником зоны пластичности
в вершине реальной трещины. Ниже ограничения (7) используются при получении критических параметров разрушения.
Поясним как работает достаточный критерий (4), (5) на отростке трещины. Напомним, что угол   уже был определен из необходимого критерия. Пусть задана острая
внутренняя трещина длиной 2l0 , перед вершиной которой материал находится в исходном
состоянии, тогда зона предразрушения отсутствует и ее длина   0 . При пропорциональном нагружении   /    c  const не происходит подрастания трещины до нагрузок
    0 , где  0 – критические напряжения для острых трещин, полученные по необходимому критерию разрушения (1). Когда нагрузка превышает критические напряжения
для необходимого критерия     0 , происходит страгивание вершины трещины и начинается неупругое деформирование материала зоны предразрушения, причем   (  ) .
Пока рассматривается простейший случай, когда зона предразрушения расположена на
продолжении трещины, а потому длина модельной трещины вычисляется следующим образом: 2l  2l0  2 . Соотношения (4) контролируют условия страгивания вершины модельной трещины. Одновременно с возникновением зоны предразрушения формируются
силовые связи в окрестности вершины модельной трещины согласно обобщенной модели
Леонова-Панасюка-Дагдейла (рис. 4). Из-за действующих силовых связей в вершине трещины имеет место устойчивый рост трещины 2l0  2l  2l  до определенного уровня
нагружения   , где   – критические напряжения для острых трещин, полученные по
достаточному критерию разрушения (4), (5), причем     0 , 2l   2l0  2 – критическая длина модельной внутренней трещины,   (  ) – критическая длина зоны
предразрушения. Соотношения (5) контролируют условия разрушения силовых связей,
действующих в зоне предразрушения. Когда длина зоны предразрушения  совпадает с
критической величиной  , устойчивый рост трещины сменяется неустойчивым.
4. Получение критических параметров разрушения
Получим соотношения, связывающие критические параметры K I , K II и  для
острой трещины, распространяющейся прямолинейно    0 в хрупком материале. Для
критических значений K I , K II ,  соотношения (4), (5) превращаются в равенства. Для
КИН K I и длины зоны предразрушения  используются первые соотношения из (4), (5),
а для КИН K II и длины зоны предразрушения  используется вторые соотношения из
(4), (5). После соответствующих преобразований получаем
 r0 *
 r0 * 
(8)
KI 
      KII 

    
2
2
2
2
 G v* 
 G u* 

  8 



8



 
 
   1 KI 
   1 K II 

(9)
Для суммарных коэффициентов интенсивности напряжений K I , K II , порождаемых
*
напряжениями   ,   , действующими на бесконечности, и напряжениями  * ,  , дей-
ствующими на отрезке [  0] , справедливо представление [12]
 2
 2
  
  
K I     l   *  l 1  arcsin 1    , K II     l   *  l 1  arcsin 1    .(10)
l 
l 


 
 
Первые и вторые соотношения в (8)–(10) эквивалентны, если имеет место пропорциональное нагружение, а тензоры напряжений и деформаций соосны. Таким образом,
получены две нелинейные системы уравнений (8), (9) относительно K I ,  или K II ,  .
Получим оценки для длины зоны предразрушения  . Соотношения (10) могут быть
существенно упрощены, когда длина нагруженного участка много меньше полудлины
трещины, т. е. l 1 . Так как
2
  
,
arcsin 1    
l  2
l

то первое соотношение (10), записанное для критических параметров, преобразуется к виду
*
,
(11)

l*
где l   l0    . Из первого соотношения (9) и (11) после соответствующих преобразоваK I*   *  l *   *  l *
2 2
ний получаем квадратное уравнение для безразмерного параметра







l






2
  

*
2 2
l

 v* G

 0.
l  1 l  *
Пренебрегая величинами высшего порядка малости, получим простое выражение для
меньшего корня квадратного уравнения
 2 2 v * G

.
l    1 l   
Если ограничение   l 
(12)
1 не выполняется, из соотношений (9), (10) получается
трансцендентное уравнение для определения   l  . Особые трудности при решении этого
уравнения отсутствуют, если оно имеет положительный корень меньше единицы.
Критический КИН K I острой внутренней трещины (11) представим в виде
 2 2  * * 
K I*   *  l * 1 
(13)
.
*
* 



l



Примем во внимание первое соотношение из (8) и уравнение (13), тогда кривая разрушения по достаточному критерию для острой внутренней трещины запишется в виде


   4   
2l 
 1
1
 *   r0  
r0






1
.
(14)
Таким образом, при пропорциональном нагружении и соосности тензоров напряжений и деформаций получена система двух нелинейных уравнений (12) и (14) относительно
критических параметров  и   , описывающая формирование зоны предразрушения и
кривую разрушения для сложного напряженного состояния, отличного от второй моды
разрушения. Очевидно, в силу эквивалентности первых и вторых соотношений в (8), (9),
что для второй моды разрушения целесообразно пользоваться эквивалентной системой
двух нелинейных уравнений

 2 2 u* G    4

,
 1
l    1 l   
 *  

2l 
  
1


r0  
r0






1
.
(15)
Сопоставим критические нагрузки, полученные по необходимым и достаточным
критериям для хрупких материалов для одних и тех же длин трещин. Из необходимого
критерия (1) имеем:
 r0 *
K I0 
   0  .

2
0
0
Учитывая, что согласно (10) K I     l0 , получаем

2l0
 0 
 1 
*

r0








1
.
Для одних и тех же длин трещин l0  l * находим
 
4 
 1
.
 0
 r0
Как видно из полученной формулы, критические нагрузки, полученные по необходимым
и достаточным критериям, могут существенно отличаться. На рис. 6 схематически показаны устойчивый (кривая 1) и неустойчивый (кривая 2) участки роста трещин, а также
кривая разрушения, полученная по необходимому критерию [13] (кривая 3). На устойчивом участке образовавшиеся новые системы воспринимают увеличивающуюся нагрузку,
так как     0 , в результате происходит подрастание трещины, поскольку l 0  l  .
Рис. 6. Устойчивый (кривая 1) и неустойчивый (кривая 2) участки роста трещин, а также
кривая разрушения, полученная по необходимому критерию (кривая 3)
В случае трещины с ответвлениями, распространяющейся в квазихрупком материале, в справочной литературе отсутствуют аналитические решения для коэффициентов
интенсивности напряжений типа (10). В общем случае K I  K I (  ,  * , , l0 ,  ) ,
K II  K II (  ,  * , , l0 ,  ) . Здесь  * ,  * , l0 ,  являются константами,   ,   ,  – переменные
параметры, поэтому можно написать K I  K I (  , ) , K II  K II (  , ) .
Для критических значений из первых соотношений (8), (9) имеем
2
 G

2  *
v*
*

  
K I (  ,  )   8 
.
(16)

*
* 
 r0
   1 K I (  ,  ) 
Зависимость K I*  K I* ( * , * ) в данном случае неявная, поэтому для решения системы
уравнений (16) предлагается следующая итерационная процедура:


*
2
( )

 i 1
 G

2  *
v*
 
K I ((  )i , (* )i ) (  )i 1  8 
 ,

*
*
 r0
   1 K I ((  )i 1 , ( )i ) 
*
где i – номер итерации. Из вторых соотношений (8), (9) получается система уравнений,
эквивалентная (16).
На каждой итерации при фиксированных значениях   ,  коэффициенты интенсивности напряжений K I  K I (  , ) и K II  K II (  ,  ) можно найти методом конечных элементов из решения задачи о растяжении пластины, ослабленной трещиной с двоякосимметричными ответвлениями под углом    0 .
Рассмотрим конкретный пример пластины, схема нагружения которой показана на
рис. 7, а. Размеры пластины 400  200 мм, l0  100 мм,   1 мм; характеристики материала: модуль Юнга E  2  105 Н/мм2, коэффициент Пуассона   0,3, предел текучести
 T  225 Н/мм2. На внешнем контуре пластины заданы равномерно распределенные
напряжения    25 Н/мм2, на отростках действуют нормальные сжимающие и касательные равномерно распределенные напряжения  *  225 Н/мм2,  *  30 Н/мм2. В силу наличия двух плоскостей симметрии расчетная область представляет правую верхнюю четверть пластины. Углы ветвления    15 , 30 , 45 . Расчетная область разбивалась на
23000 8-узловых четырехугольных и треугольных элементов, причем производилось сгущение сетки в окрестности вершины отростка с коэффициентом 100:1. На рис. 7, б показан фрагмент сетки в окрестности вершины отростка.
Рис. 7. Схема нагружения пластины с трещиной (а), фрагмент сетки в окрестности вершины отростка (б)
Результаты расчетов приведены в таблице. Для получения
коэффициентов интенсивности напряжений K I и K II использовался J-интеграл Райса [10], который в приближении плоского
напряженного состояния связан с K I и K II зависимостью

15
30
45
KI
K II
415,71 57,042
387,94 161,03
305,33 258,77
EJ  K I2  K II2 . Контурный интеграл преобразовывался в интеграл
по площади и интегрирование производилось по ближайшим к вершине отростка элементам. Разделение на I и II моды осуществлялось методом Лорензи [14]. Решение той же задачи, но при свободном от напряжений контуре трещины, сравнивалось с решением, полученным для бесконечной плоскости в случае одноосного растяжения методом сингулярных интегральных уравнений [12, стр. 68]. Было получено различие решений по K I –
14%, по K II – 10%, что можно считать приемлемым результатом, если учесть, что сравниваются решения для конечной и бесконечной областей. Результаты можно улучшить,
если использовать более мелкое разбиение.
Заключение
В работе получены критические параметры разрушения (длины зон предразрушения и нагрузки) для ветвящихся трещин в квазихрупких материалах с использованием модифицированной модели Леонова-Панасюка-Дагдейла, когда зоны предразрушения занимают прямоугольники, расположенные вдоль отростков трещины. Поперечник каждой
зоны предразрушения определяется из решения простейшей задачи теории пластичности
около вершины трещины. При формулировке критериев разрушения использовались простейшие аппроксимации диаграмм деформирования реальных материалов. Предлагаемая
модификация модели Леонова-Панасюка-Дагдейла позволяет оценить критическое раскрытие трещины и критическое смещение берегов трещины. При построении простых выражений для критических параметров разрушения используются коэффициенты интенсивности напряжений для трещины, распространяющейся прямолинейно, и коэффициенты интенсивности напряжений для трещины ветвления с отростками, когда на отростке
заданы нормальные и сдвигающие напряжения, моделирующие зону пластичности. Чтобы
построить коэффициенты интенсивности напряжений для трещины с отростками, методом конечных элементов решена задача об одноосном растяжении пластины с трещиной,
имеющей двоякосимметричное ответвление. Предложена итерационная процедура, позволяющая численно получить критические значения коэффициентов интенсивности напряжений по 1-ой и 2-ой моде в зависимости от угла ветвления трещины.
Работа выполнена при финансовой поддержке РФФИ (код проекта 07-01-00163) и
интеграционного проекта РАН № 4.12.3.
Литература
1. Корнев В.М. Ветвление и излом траекторий трещин отрыва в поликристаллах // Физическая мезомеханика. 2003. Т. 6. № 5. С. 37-46.
2. Broberg K.B. On crack paths // Eng. Fracture Mechanics. 1987. V. 28. No 5/6. P. 663-679.
3. Аннин Б.Д., Жигалкин В.М. Поведение материалов в условиях сложного нагружения.
– Новосибирск: Издательство СО РАН, 1999. – 342 с.
4. Нейбер Г. Концентрация напряжений. – М.; Л.: Гостехтеоретиздат, 1947. – 204 с.
5. Новожилов В.В. О необходимом и достаточном критерии хрупкой прочности // Прикладная математика и механика. 1969. Т. 33. Вып. 2. С. 212-222.
6. Леонов М.Я., Панасюк В.В. Развитие мельчайших трещин в твердом теле // Прикл. механика. 1959. Т. 5. № 4. С. 391–401.
7. Dugdale D.S. Yielding of steel sheets containing slits // J. Mech. Phys. Solids. 1960. V. 8.
P. 100–104.
8. Корнев В.М., Кургузов В.Д. Многопараметрический достаточный критерий квазихрупкой прочности для сложного напряженного состояния // Физическая мезомеханика. 2006. Т. 9. № 5. С. 43-52.
9. Kornev V.M., KurguzovV.D. Multiparametric sufficient criterion of quasi-brittle fracture for
complicated stress state // Eng. Fracture Mechanics. 2008. V. 75. No 5. P. 1099-1113.
10. Райс Дж. Математические методы в механике разрушений // Разрушение. Т. 2. – М.:
Мир, 1975. С. 204-335.
11. Баренблатт Г.И. Математическая теория равновесных трещин, образующихся при
хрупком разрушении // ПМТФ. 1961. № 4. С. 3–56.
12. Саврук М.П. Коэффициенты интенсивности напряжений в телах с трещинами // Механика разрушения и прочность материалов. Т. 2. – Киев: Наук. думка, 1988.
13. Kornev V.M., Kurguzov V.D. A discrete-integral strength criterion for complicated stress
states // Fatigue & Fracture of Engineering Materials & Structures. 1999. V. 22, N 11.
P. 989–995.
14. DeLorenzi H.G. On the energy release rate and the J-integral for 3D crack configurations //
Int. J. Fracture. 1982. V. 19. P.183-193.