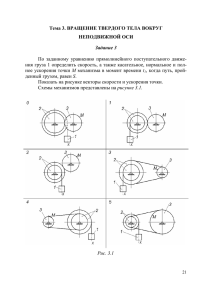
движение твердого тела вокруг неподвижной точки
advertisement

ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА, ИМЕЮЩЕГО ОДНУ НЕПОДВИЖНУЮ ТОЧКУ 1. Уравнения сферического движения твердого тела. Мгновенная ось вращения и мгновенная угловая скорость Рассмотрим движение твердого тела, одна из точек которого во все время движения остается неподвижной. При таком движении все остальные точки тела движутся по сферическим поверхностям, центры которых совпадают с неподвижной точкой. Такое движение называется сферическим. Примером сферического движения могут служить: движение тела, единственной связью которого является сферический шарнир; движение волчка, имеющего неподвижную точку. Для определения положения тела в каждый момент времени воспользуемся двумя системами осей координат: неподвижной системой Oxyz с началом в неподвижной точке O и подвижной системой Oxhz, неизменно связанной с твердым телом, с началом в той же неподвижной точке O (рис. 1). Положение тела однозначно определяется тремя углами Эйлера – ψ, θ, φ. При движении твердого тела, одна из точек которого остается неподвижной, углы ψ, θ, φ непрерывно изменяются во времени, являясь функРис. 1 циями времени t: ψ=f1(t); θ=f2(t); φ=f3(t). Эти уравнения – уравнения сферического движения твердого тела. Для рассматриваемого движения теорема Эйлера может быть сформулирована так: Всякое мгновенное движение твердого тела, имеющего одну неподвижную точку, является мгновенным вращательным движением вокруг мгновенной оси вращения, проходящей через эту точку. В отличие от вращения твердого тела вокруг неподвижной оси, y векr тора мгновенной угловой скорости w с течением времени изменяется не 1 r v r только модуль, но и линия действия. Вектор w откла- h r r дывается от неподвижной точки O по мгновенной оси r w в такую сторону, чтобы, смотря навстречу этому вектору, видеть вращение тела, происходящее против Рис. 2 движения часовой стрелки (рис. 2). Мгновенная ось представляет собой геометрическое место точек тела, скорость которых в данный момент равна нулю. 2. Угловое ускорение тела при сферическом движении При сферическом движении тела положение мгноr Dw r w O r w1 r Dw венной оси вращения со временем изменяется, а, следовательно, изменяется не только модуль, но и направле- r eср ние вектора угловой скорости тела. Пусть моменту времени t соответствует вектор угr r ловой скорости w, а моменту времени t + Dt вектор w1 r Рис. 3 r (рис. 3), Dw – приращение вектора w за время Dt. Вектор среднего углового ускорения определяется по формуле r r Dw e cp = . dt r r Направление ecp совпадает с направлением Dw. Предел этого отноше- ния при Dt ® 0 называется угловым ускорением тела в момент времени t: r r r r Dw dw r dw e = lim = ,e= . Dt ® 0 D t dt dt r Если мы будем откладывать вектор w от неподвижной точки O, то конец его опишет кривую или годограф угловой скорости (рис. 4). r Определим скорость u движения точки А - конца вектора угловой r скорости w – по годографу в момент времени t. Радиус-вектором этой r точки является вектор w, а скорость точки равна r r dw . u= dt 2 r r Так как векторы e и u равны одной и той r u же величине, то они равны между собой: r r e = u, E A т.е. угловое ускорение тела геометрически рав- r e но линейной скорости конца вектора угловой r скорости. Вектор e откладывается от непод- O вижной точки. Рис. 4 Прямая, по которой направлен вектор углового ускорения, называется осью углового ускорения и обозначается Е. 3. Скорости точек тела при сферическом движении. Формулы Эйлера На основании теоремы Эйлера вектор скорости любой точки М твердого тела, имеющего одну неподвижную точку, равен r r r v = w´ r, r uuuur r где r = OM , а w – вектор мгновенной угловой скорости тела (рис. 5). Если мы обозначим через ωx,ωy,ωz проекции вектора на неподвижные координатные оси Oxyz, а через х, у, z координаты точки М в этой же системе координат, то получим r r r r w = wx i + w y j + w z k , r r r r r = x i + yj + z k , r r r где i , j , k орты осей r w r k¢ r i r k r i¢ r j¢ r jr r Рис. 5 координат Oxyz. Тогда 3 r r r vM = w´ r r i r j r k r r r vM = w ´ r = w x w y w z = x y z r r r = (w y z - w z y )i + (w z x - w x z ) j + ( w x y - w y x ) k . r Проекции вектора vM на неподвижные оси координат v x = w y z - wz y ü ï v y = w z x - w x z ý. v z = w x y - w y x ïþ (1) (2) r В правых частях формул изменяются и проекции w и координаты точки М. Чтобы избежать последнего обстоятельства, проектируют векторное равенство (1) на подвижные оси координат Oxhz, скрепленные с телом. Аналогично получаем: r r r vx = whV - wz hü i¢ j¢ k ¢ r r r ï vM = w ´ r = wx wh wz , vh = wz x - wxz ý . (3) vz = wx h - whxïþ x h z В правых частях последних формул с течением времени изменяются только проекции векторов ωx, ωh, ωz, а координаты x, h, z точки М в подвижной системе координат, жестко связанной с телом, остаются неизменными. Формулы (2) и (3) установлены Эйлером. Модуль скорости любой точки тела имеет вид v = v x2 + v 2y + v z2 , v = vx2 + vh2 + vz2 . С другой стороны, поскольку скорость любой точки тела определяется как вращательная вокруг r w M мгновенной оси, то модуль скорости определяется h по формуле vM=hΩ·ω, O где hΩ – длина перпендикуляра, опущенного из точки Рис. 6 М на мгновенную ось вращения (рис. 6). r vM 4 4. Ускорение точек твердого тела при сферическом движении. Теорема Ривальса Для вычисления ускорения какой-либо точки тела при сферическом движении воспользуемся векторным выражением скорости этой же точки: r r r v = w´ r. Ускорение точки определяется по формуле r r r r dv dw r r dr a= = ´ r + w´ . dt dt dt Учтем, что (4) r r dw r dr r r r = e, = v = w´ r. dt dt Тогда равенство (4) принимает вид r r r r r a = e ´ r + w´ v, или r r r r r r a = e ´ r + w ´ (w ´ r ), r r r r r r где e ´ r = а вр вращательное ускорение точки; w ´ v = a oc осестремительное ускорение точки. Таким образом, r r r a = a вр + a oc . (5) Равенство (5) выражает теорему Ривальса об ускорении точки тела, совершающего сферическое движение. Ускорение любой точки твердого тела при сферическом движении определяется как геометрическая сумма ее вращательного и осестремительного ускорений (рис. 7). r ос M a r a вр r a h h r v r r K2 E r w r e Модуль вращательного ускорения опO ределяется следующим образом: K1 Ù r r a вр = e × r × sin( e, r ) = hE e, Рис. 7 где hE=MK1 – кратчайшее расстояние от точки М до оси углового ускорения Е. r Направление a вр определяется по правилу векторного произведения. 5 r r r Вектор осестремительного ускорения a oc = w ´ v направлен перпендиr r кулярно векторам w и v , т.е. по перпендикуляру, опущенному из точки М на мгновенную ось W. Модуль осестремительного ускорения определяется rÙ r a oc = wv sin( w, v ) = wv = hW w2 , где hΩ=MK2 – кратчайшее расстояние от точки М до мгновенной оси вращения W. Модуль ускорения точки как диагональ параллелограмма ускорений можно определить по формуле Ù r r a = (a ) + (a ) + 2a × a × cos(а вр , а ос ) . вр 2 oc 2 вр oc 5. Теорема об ускорении точек свободного твердого тела Ускорение точки свободного твердого тела равно геометрической сумме ускорения полюса, осестремительного ускорения точки и ее вращательного ускорения, определенных относительно мгновенных оси вращения и оси углового ускорения, проходящих через полюс. Скорость произвольной точки М свободного тела (рис. 8) равна r r r r v = v0 + w ´ r . r ос M a r a вр r a h r a вр r r a0 r K2 r w E h r e r v0 rO a0 Рис. 8 K1 Ускорение точки r r r r r dv dv0 dw r r dr a= = + ´ r + w´ , dt dt dt dt r dv0 r где = a0 ускорение полюса O; dt r dw r r r r вр ´ r= e ´ r= a вращательное ускорение dt точки М относительно оси углового ускорения E, проходящей через полюс O; r r dr r r r oc w ´ = w ´ v= a осестремительное ускорение точки M относительно dt мгновенной оси вращения W, проходящей через полюс О. Поэтому r r r r a = a0 + a вр + a oc . Теорема доказана. 6