Лекция № 10 РАСПРЕДЕЛЕНИЕ НАГРУЗКИ ПРИ ПЕРЕМЕННОМ
advertisement

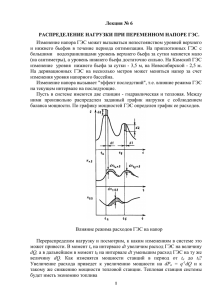
Лекция № 10 РАСПРЕДЕЛЕНИЕ НАГРУЗКИ ПРИ ПЕРЕМЕННОМ НАПОРЕ ГЭС Изменение напора ГЭС может вызываться непостоянством уровней верхнего и нижнего бьефов в течение периода оптимизации. На приплотинных ГЭС с большими водохранилищами уровень верхнего бьефа за сутки меняется мало (на сантиметры), а уровень нижнего бьефа достаточно сильно. На Камской ГЭС изменение уровня нижнего бьефа за сутки - 3,5 м, на Новосибирской - 2,5 м. На деривационных ГЭС на несколько метров может меняться напор за счет изменения уровня напорного бассейна. Изменение напора вызывает "эффект последствий", т.е. влияние режима ГЭС на текущем интервале на последующие. Пусть в системе имеются две станции - гидравлическая и тепловая. Между ними произвольно распределен заданный график нагрузки с соблюдением баланса мощности. По графику мощностей ГЭС определен график ее расходов. Влияние режима расходов ГЭС на напор Перераспределим нагрузку и посмотрим, к каким изменениям в системе это может привести. В момент tа на интервале dt увеличим расход ГЭС на величину dQ, а в дальнейшем в момент tб на интервале dt уменьшим расход ГЭС на ту же величину dQ. Как изменятся мощности станций в период от tа до tб? Увеличение расхода приведет к увеличению мощности на dPа = q-1dQ и к 1 такому же снижению мощности тепловой станции. Тепловая станция системы будет иметь экономию топлива где qа, bа - относительные приросты ГЭС и ТЭС; λа = bаqа -множитель Лагранжа; dV= dQ dt - дополнительный сток ГЭС. Экономия топлива найдена без учета изменчивости напора. В действительности увеличение расхода приводит к увеличению уровня нижнего бьефа. Так как этот процесс затухает медленно, то он будет продолжаться от tа до бесконечности. Мощность ГЭС при этом снижается на Таким образом, чтобы судить о мощностях, нужно знать изменчивость уровней нижнего бьефа dHt н.б которая требует учета нестационарных процессов в нижнем бьефе. Методы эти сложны, и получение величин dHt н.б требует трудоемких расчетов. Поэтому обычно применяются упрощенные методы. Дополнительный расход топлива ТЭС за счет увеличения уровня нижнего бьефа на dHt н.б где принято обозначение Такое обозначение введено потому, что величина ∆λа н.б. имеет ту же размерность, что и коэффициент эффективности λ по (6.24). Подобные рассуждения можно применить к моменту tб, когда будет восстановлен баланс стока ГЭС, тогда получим Но напор меняется и за счет изменчивости верхнего бьефа, поэтому необходимо учесть эффект последствия. В течение периода от tа и tб ГЭС работает с пониженными на dHв.б по сравнению с первоначальным режимом уровнями верхнего бьефа. Можно так определить снижение мощности ГЭС в этот период: 2 причем производная ∂P показывает изменение мощности ГЭС от напора, а ∂H ∂H изменение напора от объема. Всего же объем изменился на dV. Пережог ∂V топлива на ТЭС где причем легко видеть, что размерность этой величины также совпадает с размерностью λ. по (6.24). Общее изменение расхода топлива системы на основании равно: Если первоначальное распределение нагрузки было лучше второго, то dBс > 0; если же последующий режим лучше, то dBс < 0, т.е. в системе будет экономия топлива. Примем для дальнейшего условие равноэкономичности режимов за расчетное, что соответствует dBс = 0. Из последнего после сокращения dV следует Отсюда следует, что при изменении напора ГЭС значение λ, не остается постоянным. Поэтому на каждом расчетном интервале времени требуется определять свой коэффициент эффективности λ. 3 Распределение реактивных нагрузок Задача распределения реактивных нагрузок может быть также решена методом множителей Лагранжа. Поскольку генерация реактивной мощности влияет главным образом на режим напряжений и потокораспределение мощностей системы, то критерием оптимальности являются потери активной мощности. Минимизируя потери активной мощности, можно снизить и расход топлива станций системы. Запишем эту задачу. 1. Уравнение цели - минимум потерь активной мощности: π ⇒ min. 2. Уравнение связи имеет вид π(Qi), где i- номер источника реактивной мощности. 3. Уравнение ограничения - балансовое уравнение реактивных нагрузок Qн и мощностей источников реактивной мощности Qi т.е. 4. Уравнение оптимизации с использованием метода множителей Лагранжа имеет вид Вывод уравнения оптимизации. Функция Лагранжа Неизвестными в этой задаче являются r мощностей источников реактивной мощности и множитель Лагранжа λ, всего r + 1 неизвестных. Для решения задачи составляется r уравнений дифференцированием функции Лагранжа по всем независимым переменным и одно уравнение - балансовое. Дифференцируя функцию Лагранжа, получаем r уравнений: Отсюда следует: Это условие справедливо только для случаев, когда генерация реактивной мощности не связана непосредственно с затратами топлива или мало влияет на 4 них. В противном случае задачи распределения активных и реактивных мощностей должны решаться совместно. Условие упрощается, если пренебречь потерями реактивной мощности, т.е. принять ∆Q = 0, тогда условие оптимальности имеет вид Физический смысл λ. Запишем λ в конечных разностях и домножим числитель и знаменатель на ∆Q, тогда Полученное условие показывает, что оптимальным будет такой режим, при котором для всех источников реактивной мощности будет иметь место равенство прироста потерь активной мощности на единицу прироста реактивной нагрузки потребителей. Упрощенный алгоритм комплексной оптимизации режима энергосистемы Мощности электрических станций и параметры режима сети могут определяться при поэтапном решении комплексной задачи. На первом этапе определяются активные мощности станций и приближенно рассчитывается режим электрической сети, в которой считаются известными реактивные мощности в ветвях, напряжения в узлах, коэффициенты трансформации трансформаторов. На втором этапе считаются известными активные мощности станций и рассчитываются все параметры электрической сети. Если не учитывать ограничения в форме неравенств по пропускным способностям ВЛ и мощностям электростанций, то задача комплексной оптимизации может решаться методом множителей Лагранжа, причем полученные оптимизационные уравнения позволяют решать задачу поэтапно. Пусть в энергосистеме на параллельную работу включено п активных и т реактивных источников мощности, связанных с узлами нагрузки сетью произвольной конфигурации. Целевая функция такой оптимизационной задачи имеет вид 5 Ограничение по балансу активной мощности имеет вид Аналогично по реактивной мощности Здесь π и q- потери активной и реактивной мощностей в электрических сетях. Функция Лагранжа включает эти два уравнения ограничений и имеет вид Решение находится из уравнений Найдем из уравнений второй группы отношение λ2 и λ1: Обозначим ∂q = σ Qi дифференциальный показатель (относительный ∂Qi прирост) потерь реактивной мощности в сети. Он показывает, насколько возрастают потери реактивной мощности во всей электрической сети при изменении реактивной нагрузки 1-го источника на дQi. Записав это уравнение для каждого из т источников реактивной мощности и приравняв правые части, получим условие наивыгоднейшего распределения реактивных мощностей энергосистемы Обратимся теперь к уравнениям первой группы в. Запишем одно из них в виде 6 где σi — дифференциальный показатель (относительный прирост) потерь активной мощности в системе. Подставим в последние уравнение значение Ji и получаем Это общее условие наивыгоднейшего распределения активной и реактивной нагрузок в сложной энергосистеме с учетом потерь мощности в электрической сети. Если активная и реактивная мощности распределяются независимо, то это уравнение распадается на два: (*) Можно показать, что общее условие наивыгоднейшего распределения нагрузки для однородной электрической сети, т.е. для сети, у которой для всех элементов отношение удельных активного и реактивного сопротивлений r0/x0 = const, упрощается. Для таких сетей выполняется условие Условие наивыгоднейшего распределения нагрузки в однородных сетях имеет вид Используя (*), можно поэтапно оптимизировать режим энергосистемы. Кроме упомянутых ограничений, могут быть и другие: по напряжениям, углу сдвига фазы в передачах и пр. Тогда растет число множителей Лагранжа, и процесс оптимизации усложняется. Кроме того, при расчете режима сети рассчитывается и запоминается матрица коэффициентов токораспределения. При высокой размерности задачи и необходимости учета разнообразных ограничений процесс расчета плохо сходится. Все это является недостатком рассмотренного алгоритма, поэтому он применяется для концентрированных энергосистем или в совокупности с другими методами оптимизации режима. 7 Лекция № 11 Комплексная оптимизация режимов электроэнергетической системы При комплексной оптимизации любые изменения потоков мощности в сети влияют на узловые напряжения, а значит, изменение потоков активных мощностей повлияет на потоки реактивных и наоборот. Для решения комплексной задачи применяются методы нелинейного программирования. Рассмотрим схематично решение комплексной задачи. Любая задача нелинейного математического программирования может быть записана в следующей форме. Имеется функция многих переменных F(Z,P). Компоненты Z являются искомыми параметрами режима, a D включает исходную информацию о состоянии системы. Тогда для нахождения оптимального решения необходимо получить F(Z) ⇒ min при ограничениях в виде равенств и неравенств W(Z)=0; Zmin≤Z≤Zmax. Компоненты вектора параметров режима системы Z разделяются на два подмножества: Х и Y. Подмножество Y включает независимые переменные, т.е. те параметры, которые в системе могут регулироваться, на которые можно воздействовать, используя определенные средства управления, а Х включает зависимые параметры режима, т. е. те, которые могут быть вычислены по параметру Y, тогда Z(X,Y) = Z[ X(Y), Y ], отсюда min F(Z) = min F(X,Y) = min F(Y), а ограничения принимают вид W(Х,Y)=0; Xmin≤ X(Y) ≤Xmax; Ymin≤ Y ≤Ymax. В качестве уравнения связи Y(X) используются уравнения установившегося режима электрической системы (например, уравнения узловых напряжений или узловых мощностей). Чтобы найти зависимые переменные, требуется рассчитать установившийся режим. Режим должен быть допустимым и удовлетворять приведенным ограничениям. Это самостоятельная и трудоемкая сетевая задача. В алгоритмах оптимизации режима активных и реактивных мощностей ее удельный вес наибольший. 8 Деление параметров режима Z на два подмножества Х и Y понижает размерность задачи и, следовательно, облегчает вычислительный процесс. Рассмотрим основные положения решения задачи комплексной оптимизации для энергосистемы, состоящей только из тепловых электростанций. Постановка задачи. ОЭС состоит из i = 1, 2, … , М обобщенных и отдельных узлов, и имеются только тепловые станции. Параметры режима: Рг i, Qг i , активные и реактивные мощности генераторных узлов; Ui, δi, - модули напряжений и фазовые углы в узлах системы. Известны активные и реактивные нагрузки в узлах, причем они не зависят от напряжений и частоты системы. Требуется определить оптимальное распределение нагрузки по условию минимума расхода условного топлива системы. В этой задаче: 1) уравнение цели B(Z) ⇒ min. Вектор параметров Z разделяется на вектор независимых переменных Y(Ui, δi) и зависимых переменных Х(Рг i, Qг i). Тогда можно записать: 2) уравнения связи включают эквивалентные характеристики генераторных узлов (электростанций) вида Вi(Рг i), где Вi, - эквивалентный расход условного топлива, связи между параметрами Х и Y, которые имеют вид Y(X) (связи в основном неявные), уравнения ограничений, которые задаются в виде неравенств Задаются также балансовые ограничения по активным и реактивным мощностям в виде системы уравнений установившегося режима. Узел электрической системы 9 Для каждого узла баланс по мощности равен: В уравнениях WP i нб, WQ i нб - функции небаланса по активной и реактивной мощностям. Когда в стационарном режиме в узлах системы имеется баланс, то WP i нб = 0, WQ i нб = 0. Если в стационарном режиме изменить независимые переменные Ui, δi, то появится небаланс и WP i нб > 0, WQ i нб > 0. Изменяя Рг i, Qг i можно получать новый допустимый стационарный режим для новых значений Ui, δi. Задача и будет заключаться в том, чтобы найти такое решение уравнений установившегося режима, при котором В ⇒ mm. 3) уравнения оптимального управления формируются с использованием, например, метода приведенного градиента . Они позволяют от допустимого стационарного режима системы перейти к оптимальному режиму. Решение считается оптимальным, если модуль градиент-вектора ∇B функции В(X, Y) будет меньше заданного малого значения, т. е. ∇B ≤ ε . Алгоритм комплексной оптимизации может применяться для проверки допустимости напряжений в узлах и токов в ветвях при различной нагрузке системы. Можно определить мероприятия по поддержании определенного режима. В их числе уставки по напряжению для АРН (автоматических устройств регулирования напряжения на электростанциях), положение отпаек трансформаторов при регулировании их коэффициентов трансформации, мощности синхронных компенсаторов и др. Он позволяет вести контрольные расчеты режимов при изменении схемы сети. В сочетании с методами расчета статической и динамической устойчивости по алгоритму комплексной оптимизации рассчитываются допустимые потоки мощностей ВЛ и пр. Вместе с тем при управлении ЭЭС часто решаются такие задачи, которые не требуют комплексной оптимизации и в которых успешно применяются более простые методы расчета. Распределение нагрузки между агрегатами электростанций Использовав метод неопределенных множителей Лагранжа, можно получить условие наивыгоднейшего распределения нагрузки между агрегатами электростанции в виде равенства отношения приращения первичного ресурса (подведенной мощности) к приращению вторичного (полезной мощности) при соблюдении балансовых соотношений. Распределение нагрузки между агрегатами тепловых станций. Для ТЭС возникают задачи распределения нагрузки между турбинами, котлами, блоками, частями станции. Простые условия наивыгоднейшего распределения 10 получаются лишь для конденсационных турбоагрегатов, блоков и котлов. Условия наивыгоднейшего распределения нагрузки: между конденсационными турбинами между котлами между блоками Легко показать, что Условия наивыгоднейшего распределения нагрузки между частями станции аналогичны, но каждая часть представляется эквивалентной характеристикой (эквивалентными характеристиками турбин, котлов, частей станции). Условные обозначения: b k i , - относительный прирост котла, который показывает изменение расхода условного топлива котла ∆Bi при изменении паросъема на ∆Di ; b T i , - относительный прирост турбины, который показывает изменение расхода пара ∆Di при изменении мощности турбин на ∆P ; b бл – относительный прирост блока. В практических условиях на приведенные 3 условия могут накладываться ограничения, определяемые видом агрегатных характеристик. Характеристики могут иметь скачки, участки с постоянными относительными приростами и т. п. К распределению нагрузки при ступенчатых характеристиках агрегатов Если нагрузка распределяется между турбинами, которые имеют ступенчато-кусочные характеристики ( см. рисунок), то агрегаты загружаются в порядке возрастания их относительных приростов. Например, при росте нагрузки от минимальной Рmin = Pmin1 + Pmin2 вначале загружается агрегат 2, поскольку он имеет наименьший относительный прирост. Если нагрузка превышает Pmin1+ Р2 то загружается агрегат 1, затем при нагрузке, большей Р1+Р2 снова загружается агрегат 2, а при Р1+Рmax2 агрегат 1, при этом сохраняется принцип использования тех агрегатов, которые дают большую экономию топлива. Это же положение распространяется и на методику распределения нагрузки между блоками и котлами. Таким образом, если 11 агрегаты не имеют равных относительных приростов, то они загружаются в порядке возрастания относительных приростов. Более сложными являются условия распределения нагрузки для станций, имеющих теплофикационные турбины. Для них относительные приросты зависят не только от электрической мощности, то также и от расхода пара, идущего в производственные отборы, Dп. При распределении нагрузки между турбинами с отборами условия наивыгоднейшего распределения нагрузки имеют вид: где qiT qiП - относительные приросты расхода теплоты при изменении величины отбора (теплофикационного и производственного) и постоянстве электрической мощности; qi э - относительный прирост расхода теплоты при изменении электрической мощности; ∆ qi э , ∆ qi Т , ∆ qiП , βi , αi - величины, которые могут быть найдены при аналитической записи диаграммы режимов турбины. Имеется множество частных случаев тепловых схем ТЭС и состава их оборудования. Для них можно получить условия наивыгоднейшего распределения нагрузки, которые нашли широкое практическое применение. Распределение нагрузки между агрегатами гидростанций Для гидростанций наивыгоднейшее распределение нагрузки будет в том случае, когда агрегаты работают с равными относительными приростами: Из полученных условий следует, что методика решения задачи о наивыгоднейшем распределении нагрузки между агрегатами электростанций проста, если известны их характеристики относительных приростов и они удовлетворяют требованиям метода Лагранжа. 12
![Компенсация реактивной мощности [14 кб] - netron](http://s1.studylib.ru/store/data/000762066_1-873b1211dcde4ff68acd7e1641f24cdd-300x300.png)