Тема 6. Проверка гипотез о равенстве числовых характеристик
advertisement
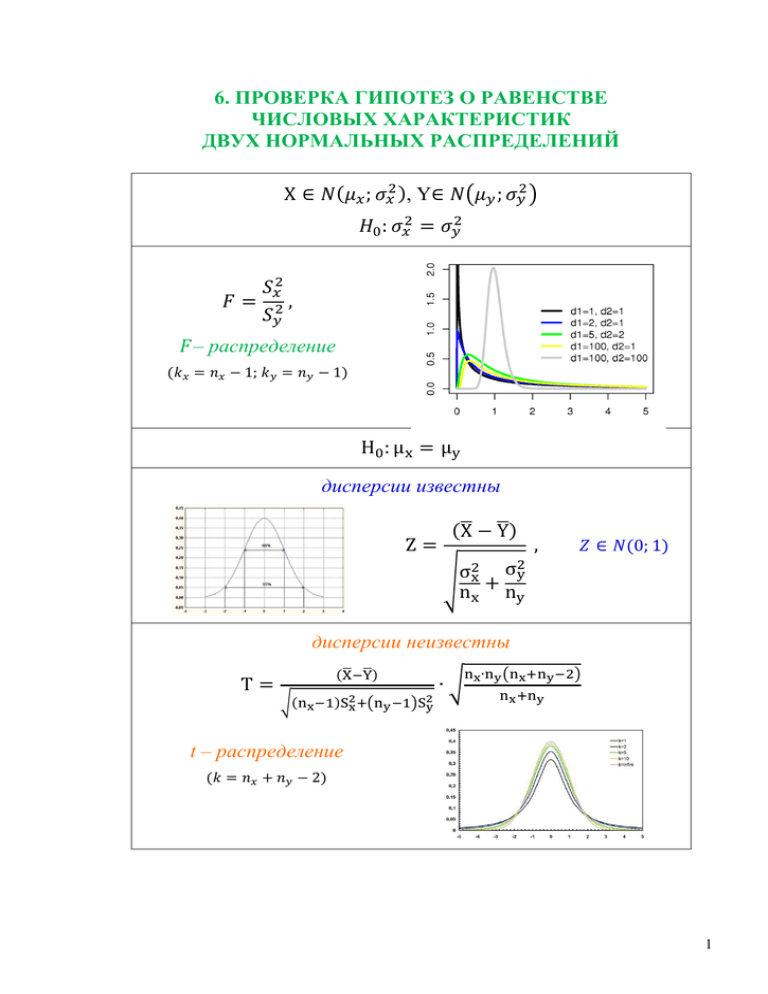
6. ПРОВЕРКА ГИПОТЕЗ О РАВЕНСТВЕ ЧИСЛОВЫХ ХАРАКТЕРИСТИК ДВУХ НОРМАЛЬНЫХ РАСПРЕДЕЛЕНИЙ ( ), Y ( ) – распределение ( ) дисперсии известны (̅ ̅) ( ) √ дисперсии неизвестны (̅ ̅) ) √( ( √ ( ) ) t – распределение ( ) 1 Практическое занятие №6 ПРОВЕРКА ГИПОТЕЗ О РАВЕНСТВЕ ЧИСЛОВЫХ ХАРАКТЕРИСТИК ДВУХ НОРМАЛЬНЫХ РАСПРЕДЕЛЕНИЙ Проверка гипотезы о числовом значении дисперсии нормального распределения Пусть Х – случайная величина, имеющая нормальный закон распределения ( ), причем числовое значение дисперсии неизвестно. Дать точный ответ на вопрос, каково числовое значение неизвестного параметра, можно обследовав всю генеральную совокупность, что сделать, как правило, нельзя. В этом случае проводят выборочные наблюдения и по их данным вычисляют выборочную исправленную дисперсию, которая дает приближенное представление о числовом значении дисперсии . В качестве критерия проверки используют величину, которая зависит от выборочных данных ( ) и по значению которой можно судить о близости исправленной дисперсии к предполагаемому значению ( : ) . Критерий при выполнении гипотезы подчиняется распределению Пирсона ( - распределение) с числом степеней свободы . Границы критической области определяют по Приложению 5. Cодержание и особенности этапов проверки статистической гипотезы приведены в табл. 1. Пример 1. Точность работы станка-автомата проверяется по дисперсии контролируемого размера изделий, которая не должна превышать 0,15. Выборочному контролю было подвергнуто 25 изделий и по результатам определена оценка дисперсии =0,25. Предполагается, что размер изделия – нормально распределенная случайная величина. Проверить гипотезу, что станок обеспечивает требуемую точность. 1. Принимаем и . 2. Назначаем . 3. Согласно проверяемой гипотезе в основе проверки лежит критерий: ( ) имеющий асп еделение Пи сона ( свободы 4. Согласно гипотезе ) п ( п ( 5. ( ) ( - распределение) с числом степеней . критическая область W – правосторонняя: (по Приложению 5). ) ) Т.к. на л п на л нулевая гипотеза отвергается. Ста- нок не обеспечивает требуемой точности. Таблица 1 ( ; 1. Выбор гипотез 2. Назначение ) доп 3. Критерий ( – распределение ) на л Приложение 5 4. Критическая область 5. Критерий отклонения Левосторонняя ) ле ( на л ле Двусторонняя )и п ( ⁄ ⁄ ) ле ( ле или на л на л Правосторонняя ) п ( на л п п 2 Проверка гипотезы о равенстве дисперсий двух нормальных распределений Пусть имеются две случайные величины, имеющие нормальный закон распределения, причем числовые значения параметров неизвестны. В этом случае проводят выборочные наблюдения и по их данным вычисляют выборочные исправленные дисперсии, оценивающие неизвестные дисперсии. После определения исправленных дисперсий две случайные величины именуют: случайную величину с большей исправленной дисперсией называют Х, а с меньшей – Y. В основу проверки данной гипотезы положен критерий: , который при выполнении гипотезы имеет распределение Фишера ( - распределение) с числом степеней свободы и . Границы критической области определяют по соответствующему Приложению 7. Cодержание и особенности этапов проверки статистической гипотезы приведены в табл. 2. Пример 2. Рабочий в начале смены настроил два станка-автомата. Предварительным анализом было установлено, что размер диаметра валиков, изготовленных каждым автоматом, имеет нормальный закон распределения. В конце смены был проведен выборочный контроль 14 деталей, обработанных на первом станке, и 9 деталей - на втором станке и исправленные дисперсии соответственно составили 5 мм и 7 мм . Проверить гипотезу о том, что два станка-автомата имеют одинаковую точность. На предварительном этапе именуем выборки: с большей дисперсией – X, с меньшей – Y: , следовательно, и . 1. Принимаем и . 2. Назначаем . 3. Согласно проверяемой гипотезе в основе проверки лежит критерий: , имеющий распределение Фишера ( - распределение) с числом степеней свободы 4. Согласно гипотезе ) п ( 5. и . критическая область W – правосторонняя: ) (по Приложению 7). ( . Т.к. на л п автоматы имеют одинаковую точность. нулевая гипотеза принимается. Станки- на л Таблица 2 ( 1. Выбор гипотез ), Y ; 2. Назначение ( или ) доп 3. Критерий – распределение на л Приложение 7 4. Критическая область п 5. Критерий отклонения Двусторонняя ( ⁄ )и ле на л на л или ле п Правосторонняя ) п ( на л п п 3 Проверка гипотезы о равенстве математических ожиданий двух нормальных распределений при известных дисперсиях Пусть Х и Y – случайные величины, имеющие нормальный закон распреде( ), ( ), причем числовые значения математического ления ожидания неизвестны, а числовые значения дисперсии известны. В этом случае проводят выборочные наблюдения и по их данным вычисляют выборочное среднее арифметическое (соответственно ̅ и ̅ ), которое дает приближенное представление о числовом значении математического ожидания. В качестве критерия проверки используют величину, которая зависит от выборочных данных ( ̅ и ̅) и по значению которой можно судить о близости выбо( ̅ ̅) рочных средних арифметических двух распределений: . √ Выбранный критерий при выполнении гипотезы подчиняется стандартному нормальному закону распределения - Z ( ). Границы критической области ( ) находят по таблице интегральной функции Ф(z) Лапласа (Приложение 2). Подробное содержание и особенности этапов проверки статистической гипотезы с известными дисперсиями приведены в табл. 3. Таблица 3 1. Выбор гипотез ( ), ( ), дисперсии известны , или , или и 2. Назначение доп 3. Критерий (̅ ̅) ( ) Приложение 2 √ 4. Критическая область Левосторонняя ( Двусторонняя ( ) на л ; п ле 5. Критерий отклонения ) Правосторонняя ( ) п ле ле на л на л или ле на л п п Пример 3. Рабочий в начале смены настроил два станка-автомата: X и Y. Предварительным анализом было установлено, что размер диаметра валиков, изготовленных каждым автоматом, имеет нормальный закон распределения с дисперсией 5 мм для станка X и 7 мм для станка Y. В конце смены был проведен выборочный контроль 14 деталей, обработанных на станке X, и 9 деталей - на станке Y. Средние диаметры валиков соответственно составили: для автомата X – 182 мм, для Y – 185 мм. Проверить гипотезу о том, что два станка-автомата настроены на один размер. 1. Принимаем и . 2. Назначаем . 3. Согласно проверяемой гипотезе в основе проверки лежит критерий: ( ̅ ̅) , ( ) √ 4. Согласно гипотезе критическая область W – левосторонняя: 4 ( 5. и по Приложению 2 на одим ) ( на л ) Т.к. √ на л ле и ле . нулевая гипотеза отвергается, т.е. считаем, что различие выборочных средних неслучайно и станки не настроены на один размер. Проверка гипотезы о равенстве математических ожиданий двух нормальных распределений при неизвестных, но равных дисперсиях Пусть Х и Y – случайные величины, имеющие нормальный закон распреде( ), ( ), причем числовые значения математического ления ожидания и дисперсии неизвестны. В этом случае проводят выборочные наблюдения и по их данным вычисляют выборочное среднее арифметическое (соответственно ̅ и ̅ ), которое дает приближенное представление о числовом значении математического ожидания, а также выборочную исправленную дисперсию, оценивающую неизвестную дисперсию ( и ). Применяемый в данном случае критерий Стьюдента предполагает равенство неизвестных дисперсий. Поэтому на предварительном этапе необходимо убедиться в этом предположении ( - см. пример 2). В основу проверки данной гипотезы положен критерий: ( ̅ ̅) ) √( ( ( √ ) ) который при выполнении нулевой ги- потезы имеет распределение Стьюдента (t – распределение) с числом степеней свободы . Границы критической области ( ) определяют по соответствующей таблице (Приложение 6). Для односторонней критической области находят по заданному уровню значимости , помещенному в нижней строке таблицы; для двусторонней - в верхней строке. Далее проверяется принадлежность на л критической области W. Подробное содержание и особенности этапов проверки статистической гипотезы при неизвестных, но равных дисперсиях приведены в табл. 4. Пример 4. Рабочий в начале смены настроил два станка-автомата. Предварительным анализом было установлено, что размер диаметра валиков, изготовленных каждым автоматом, имеет нормальный закон распределения. В конце смены был проведен выборочный контроль 14 деталей, обработанных на первом станке, и 9 деталей - на втором станке. Средние диаметры валиков составили: для первого автомата – 182 мм, для второго – 185 мм, а выборочные исправленные дисперсии соответственно 5 мм и 7 мм . Проверить гипотезу о том, что два станка-автомата настроены на один размер. На предварительном этапе именуем выборки: с большей дисперсией – X, с меньшей – Y: , следовательно, и . 1. Принимаем и . 2. Назначаем . Дополнительно проверяем условие равенства дисперсий (см. пример 2). 3. Согласно проверяемой гипотезе в основе проверки лежит критерий: ( ̅ ̅) √( ) ( ) √ ( ) , имеющий распределение Стьюдента ( - распреде- ление) с числом степеней свободы . 4. Согласно гипотезе критическая область W – левосторонняя: по Приложению 6 находим одностороннюю критическую точку ) ) ; . однос ( однос ( ле 5 5. на л ( √( ) ) ( √ ) ( ) . Т.к. на л ле нулевая гипотеза не противоречит опытным данным. Можно сделать вывод, что различие выборочных средних случайно и станки настроены на один размер. 1. Выбор гипотез ( ), Таблица 4 ), дисперсии неизвестны, но равны , или , или ( и 2. Назначение доп (дополнительно) Проверка гипотезы 3. Критерий (̅ ̅) √( ) ( ) ( √ ) – распределение, 4. Критическая область Двусторонняя Левосторонняя однос ( , ) д с ( Правосторонняя ) ; п ле Приложение 6 однос ( ) п ле 5. Критерий отклонения на л ле на л на л или ле на л п п Задачи для самостоятельной ра оты Задача 1. Из нормальной генеральной совокупности извлечена выборка объема n = 17 и по ней найдена исправленная выборочная дисперсия 0,24. Требуется проверить гипотезу о числовом значении дисперсии: 02 = 0,18. Задача 2. По двум независимым выборкам, объемы которых n1 = 11 и n2 = 14 (распределенным нормально), найдены исправленные выборочные дисперсии = 0,76 и = 0,38. Требуется проверить гипотезу о равенстве дисперсий двух нормальных распределений. Задача 3. По двум независимым выборкам, объемы которых = 40 и = 50, извлеченным из нормальных совокупностей с известными дисперсиями и , найдены выборочные средние: 130 и 140 соответственно. Требуется проверить гипотезу о равенстве математических ожиданий. Задача 4. По двум независимым малым выборкам, объемы которых n = 12 и m = 18, извлеченным из нормальных совокупностей с неизвестными параметрами, найдены выборочные средние: 31,2 и 29,2 и исправленные дисперсии: 0,84 и 0,40. Требуется проверить гипотезу о равенстве математических ожиданий. Задача 5. Из двух партий изделий, изготовленных на одинаково настроенных станках, извлечены малые выборки. Результаты для контролируемых размеров I и II станков: I станок 3,4 3,5 3,7 3,9 II станок 3,2 3,4 3,6 ni 2 3 4 1 mi 2 2 8 Требуется проверить гипотезу о равенстве средних размеров изделий. Предполагается, что результаты измерений распределены нормально и выборки независимы. 6

