2 РАВНОВЕСНЫЕ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ ГИББСА 2.1
advertisement

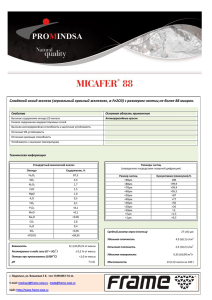
2 РАВНОВЕСНЫЕ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ ГИББСА Продолжим рассмотрение термодинамических систем. В данной теме в отличие от предыдущей будем использовать их микроскопическое представление, понимая под этим, что любой физический объект состоит из тех или иных частиц (электроны, атомы, молекулы и т. п.). При этом естественно считать, что вся совокупность частиц системы в конечном счете формирует ее наблюдаемые свойства. Основной подход, существующий в настоящее время, при исследовании таких систем основан на предположении, что любую макроскопическую систему следует рассматривать как динамическую систему, так, как это понимается в механике. Естественно, что для термодинамических систем основной формой движения частиц будет тепловое движение. В этих условиях рассмотрим методы количественного описания свойств макроскопических систем. При подготовке данной темы использовалась в первую очередь литература [4, 5, 7]. Дополнительная литература будет указана по тексту изложения. 2.1 Метод Гамильтона в классической механике Рассмотрим макроскопическую систему, состоящую из N частиц. Это могут быть по своей природе однотипные или разнотипные частицы. В данном случае будем рассматривать явления, которые определяются движением частиц как целого, т. е. частицы представляются как бесструктурные. В классической механике состояние системы в любой фиксированный момент времени определяется значениями координат r1 , ..., rN и импульсов p1 , ..., pN частиц. Будем использовать обозначения хi = (ri , pi ) , i = 1, ..., N, (2.1) X = (х1 , ..., хN ) . (2.2) При дальнейших обсуждениях важная роль будет отводиться энергии системы. Будем ее представлять функцией Гамильтона, полагая, что для нее отсутствует явная зависимость от времени. 36 Если для системы задана функция Гамильтона H(X) , то значения X(t) находятся как решения уравнений Гамильтона ∂H(X) ˙ ∂H(X) r˙ i = , pi = − . ∂pi ∂ri (2.3) Эта система 2N уравнений позволяет определить единственным образом значения ri , pi во все моменты времени по их начальным значениям ri (0) , pi (0) в некоторый момент времени t = 0 . Такую ситуацию называют полным представлением состояния объекта. Любые функции координат и импульсов частиц A = A(X) называют функциями динамических переменных. Примеры таких величин: энергия E(X) = H(X) , полный импульс p = = са системы M N i=1 N i=1 pi и момент импуль- [ri , pi ] . Значения функций динамических переменных A(X) устанавливаются из решений уравнений (2.3) для X(t) . В то же время можно использовать самостоятельные уравнения для динамических функций Ȧ(X) = N ∂A i=1 ∂A ˙ r˙ i + p ∂ri ∂pi i (2.4) или после подстановки выражения (2.3) Ȧ(X) = N ∂A ∂H i=1 ∂A ∂H − . ∂ri ∂pi ∂pi ∂ri (2.5) Выражение в правой части соотношения (2.5) – скобки Пуассона для двух динамических функций A(X) и H(X) . В символьной форме для уравнения (2.5) имеем Ȧ(X) = [H A] . (2.6) 2.2 Классические ансамбли. Функции распределения в фазовом пространстве Рассмотрим возможности метода Гамильтона в применении к макроскопическим системам. Как следует из п. 2.1, в первую очередь при исследовании того или иного объекта необходимо задать конкретный 37 вид функции Гамильтона H(X) . В силу бесконечной сложности реальных объектов невозможно учесть все факторы, которые формируют эту функцию. Единственное, что в этом случае можно сделать, это задать модель рассматриваемой системы, для которой функция H(X) будет записана точно. Таким образом, используется приближенное представление реального объекта. Предположим, что функция H(X) для системы установлена. Тогда решения ri (t) и pi (t) получают из системы 2N уравнений (2.3). Для макроскопических систем число частиц имеет порядок 1023 . Даже если бы существовала идеальная ЭВМ, способная решить такое число уравнений, получаемые решения не давали бы ответы на все вопросы по определению характеристик макроскопической системы. В первую очередь это связано с тем, что в силу непрерывного взаимодействия большого числа частиц друг с другом невозможно указать состояние X0 системы для некоторого момента t0 . В этом случае такую ситуацию определяют как неполное представление состояния динамической системы. Единственное, что в этом случае можно сделать, это рассматривать координаты и импульсы частиц макроскопической системы для любого момента времени t как случайные величины. Тогда для описания поведения таких динамических систем естественно дополнительно привлечь методы теории случайных величин и теории случайных функций. В этом случае теорию называют статистической механикой или статистической физикой. Если объект исследований – термодинамическая система, то используют термин "статистическая термодинамика". Центральная роль при таком представлении отводится функции распределения, которая по своему содержанию указывает на вероятность возможных состояний системы, находящейся в заданных условиях. Общепринято, что определение функции распределения для термодинамических систем проводится с использованием представления статистического ансамбля Гиббса. Под этим понимают полный набор возможных состояний системы по X , в которых она может находиться в процессе своей динамической эволюции. Для рассматриваемых в данном случае представлений целесообразно ввести понятие фазового пространства или Γ -пространства системы. Под фазовым пространством понимают абстрактное про38 Рис. 2.1 Схематическое представление выделенного объема dX около точки X в фазовом пространстве странство, по прямоугольным (декартовым) осям которого отложены координаты и импульсы частиц, образующих систему. Соответственно, любому состоянию системы с заданными значениями X – микросостояние системы – в фазовом пространстве будет соответствовать изображающая точка. Совокупность изображающих точек будет представлять статистический ансамбль системы, которому будет соответствовать некоторая область фазового пространства. Естественно, что даже для одной и той же системы, но находящейся в различных внешних условиях, в общем случае будут соответствовать различные области фазового пространства. Выделим в фазовом пространстве объем dX около точки X , как показано на рис. 2.1. Пусть в данный момент времени t в этом объеме заключены точки, характеризующие состояния dN систем ансамбля из их полного числа N . Тогда предел отношения этих величин dN lim = f (X, t) dX (2.7) N →∞ N определяет плотность распределения микросостояний в исследуемом ансамбле в момент времени t . Часто плотность распределения вероятности называют функцией распределения. Условие нормировки функции распределения имеет вид f (X, t) dX = 1 39 (2.8) или более подробно f (х1 , ..., хN , t) dх1 ...dхN = 1. (2.9) 2.3 Уравнение Лиувиля Временная эволюция функции распределения f (X, t) макроскопических состояний системы происходит в результате изменения со временем расположения точек х1 , ..., хN , характеризующих состояние систем ансамбля в различные моменты времени. Это изменение, в свою очередь, можно представить как течение "газа" систем ансамбля в 6N -мерном фазовом пространстве. Поскольку полное число систем ансамбля предполагается заданным (т. е. нет источников и стоков), то для функции f (X, t) можно записать соответствующее уравнение непрерывности ∂f + divX Ẋf (X, t) = 0. ∂t Запишем это уравнение в развернутом виде: (2.10) N ∂f ∂ ˙ ∂ ˙ ri f + p f = 0. + ∂t i=1 ∂ri ∂pi i (2.11) Член, стоящий под знаком суммы, можно представить в виде ∂ ˙ ∂ ˙ ∂ ∂ ri + pi f + r˙ i f + p˙ i f. ∂ri ∂pi ∂ri ∂pi (2.12) Используя уравнения движения (2.3), убеждаемся, что первый член в правой части этого выражения равен нулю. В результате, снова используя (2.3), получим следующее уравнение для функции распределения – уравнение Лиувилля: N ∂f ∂H ∂f ∂H ∂f + − = 0. ∂t i=1 ∂pi ∂ri ∂ri ∂pi (2.13) Его можно записать в более компактной форме с использованием скобок Пуассона: ∂f + [H f ] = 0. (2.14) ∂t Уравнение Лиувилля является уравнением в частных производных первого порядка. Решение начальной задачи для такого уравнения, т. е. 40 отыскание функции распределения f (X, t) по заданной функции в начальный момент времени t0 , (функции f (X0 , t, t0 ) ), эквивалентно в общем случае решению уравнений характеристик. Но последние, как легко видеть из уравнения (2.13), совпадают с уравнениями движения Гамильтона (2.3). Именно, если известно решение уравнений Гамильтона X = X(X0 , t − t0 ), (2.15) то, разрешая это равенство относительно X0 , X0 = X0 (X, − (t − t0 )) , (2.16) можно записать решение уравнения Лиувилля в виде f (X, t) = f (X0 (X, − (t − t0 )) , t0 ) . (2.17) Отметим, что X – это 6N-мерный вектор, поэтому соотношение (2.15) – система 6N алгебраических уравнений. Итак, для нахождения решения уравнения Лиувилля в общем случае надо знать решение уравнений Гамильтона. Задача, как мы уже говорили, для макроскопических систем невыполнимая. Таким образом, переход от уравнений механики к уравнению Лиувилля не приводит к упрощению без дополнительных условий. Смысл дополнительных условий состоит в том, чтобы, отказавшись от полного решения задачи, эквивалентного решению уравнений движения (2.3) и дающего исчерпывающее детальное описание системы, найти приближенные решения, описывающие статистические закономерности. Из уравнения (2.14) следует, что если скобки Пуассона равны ну∂f лю, то функция распределения f стационарна, т. е. = 0 . Равенство ∂t нулю скобок Пуассона возможно, если функция распределения зависит от X через интегралы движения. Для вопросов, которые обсуждаются, наибольший интерес представляет интеграл энергии системы E = = H(X) . Действительно, именно функцией Гамильтона определяется вид уравнений движения частиц. Сохранение интегралов импульса p(X) и момента импульса M (X) является лишь следствием уравнений движения. Вполне очевидно, что если f = f (H(X)) , то [H f ] = 0, что следует из определения скобок Пуассона. 41 (2.18) 2.4 Средние значения функций динамических переменных Среднее значение для функций динамических переменных A(X) в момент времени t определяется равенством A(t) = A(X)f (X, t) dX, (2.19) где полагается, что случайные X изменяются непрерывно. Выражение (2.19) соответствует стандартным представлениям теории вероятности, где A(t) – первый (начальный) момент случайной величины A(X) . Если функция распределения стационарна, то получаем выражение A= A(X)f (X) dX. (2.20) В частности, если исследуемой функцией является функция Гамильтона H(X) , то имеем H(X) = H(X)f (X) dX. (2.21) Определяют, что выражения (2.19) – (2.20) представляют средние по статистическому ансамблю или фазовые средние. На данном этапе подведем итоги рассматриваемого моделирования макроскопической системы как динамического объекта. 1. Состояние системы в данный момент времени полностью задается некоторой функцией распределения f (X, t) , удовлетворяющей условию (2.8). 2. Наблюдаемые значения A(t) функций динамических переменных A(X) рассчитываются по формуле (2.19). Таким образом, следует считать, что задача по исследованию свойств динамических систем в принципе решена. В то же время следует представлять, что если идет речь о термодинамических системах, то полученный результат требует существенных дополнений. Дело заключается в том, что любая термодинамическая система определяется не только величинами, которые следует рассматривать как функции динамических переменных, например энергия системы E , но и величинами, которые не имеют место в представлениях механики, например температура T системы. Обсуждение таких дополнений будет сделано далее при установлении равновесных функций распределений п. 2.7 – 2.9 и в законченной форме в части 3. 42 В заключение отметим, что существует второй способ определения среднего для произвольной функции динамических переменных A(X) – среднее по времени. Определение временного среднего Ã имеет вид 1 Ã = lim AT = lim T →∞ T →∞ T T A(t)dt, (2.22) 0 где Ã исследуется на интервале времени T . В выражении (2.22) функция A(t) рассматривается как случайная функция. Для расчета среднего в данном случае надо строить математический аппарат, отличный от выше рассмотренного. Некоторые вопросы такого подхода будут обсуждаться в последующем (часть 8). В конечном счете возникает вопрос о соотношении фазовых и временных средних. Выяснение условий, при которых такое равенство имеет место, является одной из проблем эргодической теории. Отправной точкой таких исследований является эргодическая гипотеза, утверждающая, что для равновесных систем фазовые и временные средние совпадают, т. е. A = Ã . Обсуждение этой темы можно найти, например, в литературе [8]. 2.5 Чистые и смешанные состояния. Квантовый ансамбль. Матрица плотности Переходим к рассмотрению макроскопических систем в представлениях квантовой механики. Как известно, методы исследований классической и квантовой физики носят различный характер. Сущность различия выражается принципом неопределенности: координата и импульс частицы не могут быть определены одновременно с произвольной точностью. Произведение ошибок измерения определяется выражением ΔxΔpx h, (2.23) где h – постоянная Планка. Тогда следует ожидать, что какие бы теории ни строились на соотношении (2.23), во всех случаях они будут носить вероятностное содержание. Это относится и к квантовой механике. Проведем последовательное рассмотрение схемы получения наблюдаемых величин в квантовой механике. 43 Состояние квантовой системы задается волновой функцией ψ(q, t) , где через q обозначены координаты частицы r или, для рассматриваемого случая, совокупность координат всех N частиц системы (r1 , ..., rN ) . Динамическое состояние системы определяется уравнением1 ih̄ ∂ψ = Ĥψ, ∂t (2.24) где Ĥ – оператор Гамильтона, который в символической (операторной) форме представляет полную энергию системы. Уравнение (2.24) представляет нестационарное уравнение Шредингера. Если потенциальная энергия системы от времени не зависит, то оператор Ĥ будет зависеть только от координат. Такое динамическое состояние системы называют стационарным. В этом случае пространственная и временная зависимости волновой функции ψ(q, t) могут быть разделены. Для временной зависимости функции полагают E ψ(t) = exp −i t , h̄ (2.25) тогда из выражения (2.24) получают уравнение для пространственной зависимости волновой функции Ĥψ(q) = Eψ(q), (2.26) где E – постоянная, имеющая в данном случае смысл энергии. Таким образом, для стационарных состояний волновая функция имеет вид ψ(q, t) = ψ(q) · ψ(t). (2.27) Плотность вероятности таких состояний не зависит от времени |ψ(q, t)|2 = |ψ(q)|2 . (2.28) Явный вид волновой функции находят из уравнения (2.26). Само решение уравнения (2.26) требует выполнения условий для волновой функции. Она должна быть однозначной, непрерывной и ограниченной вместе со своими производными и удовлетворять условию нормировки 1 ны. |ψ(q)|2 dq = 1 (2.29) Полагается, что представления квантовой механики к настоящему моменту извест- 44 или в общем виде ψ ∗ ψdq = 1. (2.30) В большинстве представляющих интерес случаев решения для уравнения (2.26) существуют не при любых E , а лишь при строго определенных значениях, которые образуют энергетический спектр исследуемой системы En1 , En2 , ..., Eni , ... . Значения En называются собственными значениями, а функции ψni , являющиеся решениями уравнения (2.26) при E = Eni , называют собственными функциями, где через n обозначены квантовые числа, индекс i при n указывает на конкретные значения квантовых чисел. В связи с этим следует понимать, что волновая функция ψ(q) в уравнении (2.26) является одной из собственных функций ψn . Если для исследуемой системы, для которой осуществлено решение уравнения (2.26), выбирается некоторое En с соответствующей ψn , то волновая функция ψ(q) такой системы определяется полностью. Эту ситуацию, когда волновые функции системы полностью определены, называют чистыми состояниями. Однако могут быть ситуации, когда для состояния системы невозможно установить волновую функцию. Это может быть в том случае, когда какое-либо чистое состояние по каким-либо причинам не может однозначно характеризовать состояние системы. Состояния, которым невозможно сопоставить никакую волновую функцию, называют смешанными состояниями. Единственный выход в рамках рассматриваемых представлений – это определить вероятности wn для чистых состояний. Тогда смешанное состояние системы будет описываться не волновой функцией ψ(q) , а набором вероятностей wn1 , wn2 , ..., wni , ... , с которыми чистые состояния ψn1 , ψn2 , ..., ψni , ... входят в смешанное. Если соответствующие вероятности установлены, то можно вычислить наблюдаемые значения физических величин для систем, находящихся в смешанном состоянии. Для энергии системы E по определению среднего получаем E= n En wn , (2.31) где суммирование ведется по всем значениям квантовых чисел n . Выражению (2.31) следует придать более точное представление, а именно E = n En wn , 45 (2.32) где в данном случае использован тот факт, что собственное значение En следует рассматривать как среднее квантовомеханическое, т. е. En . Таким образом, следует ожидать, что при описании квантовых систем в смешанном состоянии надо использовать два последовательных процесса усреднения: первое усреднение (квантовомеханическое) связано в конечном счете с принципам неопределенности, а второе (статистическое) – с неопределенностью состояния системы. Отметим, что случай смешанного состояния является типичным для термодинамических систем, которые собственно и являются объектом нашего рассмотрения. Рассмотрим, каким образом могут быть определены вероятности wn для квантовых систем. По аналогии с классическими системами (см. п. 2.2) вводится представление статистического ансамбля как полного набора чистых состояний системы, находящейся в некоторых заданных условиях. В любой момент времени t система будет находиться в одном из возможных чистых состояний с некоторой вероятностью wn . Если система испытывает внешнее воздействие, то ее статистический ансамбль и соответственно вероятность будут изменяться с течением времени, т. е. wn = wn (t) . Это обсуждение, конечно, не указывает способа получения аналитического выражения для wn . При вычислении средних в квантовой механике используют представление величин в операторной форме. Результаты, которые выше представлены для энергии, можно обобщить на любой оператор λ̂ , имея в виду, что и для него справедливо уравнение λ̂ψ = λn ψ, (2.33) где λn – собственные значения, ψ – собственные функции оператора λ̂ , например в q -представлении, т. е. ψ = ψ(λ, q) . Часто используется матричное представление операторов. При исследовании систем, находящихся в смешанном состоянии, удобно ввести специальную матрицу ρ(q, q ) = n wn ψ ∗ (n, q )ψ(n, q), (2.34) называемую матрицей плотности системы. Покажем, что с помощью выражения (2.34) вычисляются средние величины таких систем. Общее определение среднего для некоторой величины λ есть λ = n wn λn , 46 (2.35) где wn – вероятность n -го состояния. Среднее значение λ в квантовой механике определяется известным выражением λ = ψ ∗ (n, q )λ̂ψ(n, q)dq. (2.36) Подставим выражение (2.36) в (2.35) и поменяем порядок суммирования и интегрирования. При этом оператор λ̂(q) представим в виде матрицы δ(q − q )λ̂(q )dq ≡ λ̂(q) = λ(q , q)dq . (2.37) Тогда выражение для среднего приводится к виду λ = dq dq = n dq wn ψ ∗ (n, q )λ(q, q )ψ(n, q) = (2.38) dq λ(q, q )ρ(q , q), где использовано определение (2.34). В такой форме получается диагональный элемент произведения матриц λ · ρ , т. е. dq λ(q, q )ρ(q , q), (2.39) проинтегрированный по dq . Сумма диагональных элементов любой матрицы типа Ajj или интеграл по диагональным элементам A(q, q) , если значок меняется непрерывно, называется следом или шпуром матрицы ( Sp ), т. е. Sp A = Ajj , (2.40) j или Sp A = dqA(q, q). (2.41) Тогда выражение (2.38) следует записать как λ = Sp (λ · ρ), (2.42) где λ · ρ – произведение двух матриц: матрицы плотности и матрицы усредняемой величины. Значение формулы (2.42) в том, что она не зависит от выбранного представления, как это и необходимо для всякой физической величины. Исследуем некоторые свойства матрицы плотности. Определим шпур самой матрицы. Для этого в соотношении (2.42) положим λ = 1 . Отсюда получаем Sp ρ = 1. (2.43) 47 Установим шпур квадрата матрицы. Используем правило перемножения матриц (ρ · ρ)qq = dq ρ(q, q ) · ρ(q , q ). (2.44) Тогда подставив выражение для матриц ρ(q, q ) и ρ(q , q ) переставив порядок суммирования и интегрирования по dq , получим = n,n dq ρ(q, q ) · ρ(q , q ) = wn wn ψ ∗ (n, q)ψ(n , q ) = n ψ ∗ (n , q )ψ(n, q )dq = (2.45) wn2 ψ ∗ (n, q)ψ(n, q ). Чтобы найти шпур этого выражения, полагаем q = q и интегрируем по dq . Тогда получаем Sp (ρ · ρ) = wn2 . (2.46) n Шпур самой матрицы плотности есть Sp ρ = n wn ψ ∗ (n, q)ψ(n, q)dq = n wn = 1. (2.47) Если вероятность события недостоверная, то wn < 1 . Тогда, очевидно, wn2 < wn . Аналогичное соотношение получается для выражений (2.46) и (2.47) Sp ρ · ρ ≤ Sp ρ. (2.48) Неравенство (2.48) переходит в равенство только для случая чистого состояния системы, когда одна из вероятностей wn = 1 , а все остальные wn =n = 0 . Тогда имеем Sp ρ · ρ = Sp ρ = 1. (2.49) Из приведенного следует, что матрица плотности дает максимально полное описание смешанного состояния системы. Найдем уравнение для изменения матрицы плотности со временем. Для этого возьмем производную от матрицы плотности (2.34) ∂ψ ∗ ∂ψ ∂ρ(q, q ) = wn ψ + ψ∗ . ∂t ∂t ∂t n 48 (2.50) Используя уравнение Шредингера (2.24), получаем ∂ρ(q, q ) = Ĥ ∗ (q )ρ(q , q) − Ĥ(q)ρ(q , q) ih̄ ∂t или в символической форме (2.51) ∂ ρ̂ = [Ĥ ρ̂]. (2.52) ∂t Так как это уравнение записано в операторной форме, то оно справедливо в любом представлении. Уравнение (2.52) можно рассматривать как квантовый аналог уравнения Лиувиля (см. п. 2.3). В частности, если матрица плотности есть ∂ ρ̂ функция Ĥ , то получаем [Ĥ ρ̂] = 0 и соответственно = 0 , т. е. мат∂t рица плотности стационарна. ih̄ 2.6 Принцип равной вероятности. Микроканоническое распределение В этом параграфе и в последующих данной части переходим к установлению явного вида функций распределений для равновесных термодинамических систем. Искомые функции должны удовлетворять уравнению Лиувилля (для классических и квантовых систем). В то же время совершенно очевидно (см. п. 2.3 и 2.5), что непосредственное решение уравнений невозможно для макроскопических систем вследствие неполного представления их состояния. Рассмотрим, каким образом получают информацию в этом случае. Для равновесных систем их полная энергия не зависит от времени. В связи с этим функция распределения f (X, t) не зависит от времени для классических систем, т. е. f (X, t) = f (X) . При этом общим решением уравнения Лиувилля является произвольная функция всех интегралов движения. Если рассматривать только внутреннюю энергию системы, то в качестве такого интеграла следует выбрать H(X) . Тогда зависимость f = f (X) проявится через зависимость f = f (H(X)) . Конкретный вид функции Гамильтона и функций распределения зависит от условий, в которых находится система, т. е. от внешних параметров a = (a1 , ..., an ) . Таким образом, для функции Гамильтона имеем представление H = H(X, a) , для функции распределения – f = f (X, a) . 49 Рассмотрим изолированную равновесную термодинамическую систему, как это было определено в п.1.1. Условие изолированности системы при заданных внешних условиях, используя определение функции Гамильтона, можно выразить равенством (2.53) H(X, a) = E = const, а функцию распределения представить в виде (2.54) f = f (H(X, a), E) . Это и определяет конкретный вид функции распределения f (X, a, E) = Cδ (H(X, a) − E) (2.55) с учетом условия нормировки (2.56) f (X, a, E)dX = 1. Благодаря наличию в этом выражении δ -функции из всех возможных значений X выделяются те, которые совместимы с условием (2.53). Постоянную C находим из условия нормировки (2.56) C= δ (H(X, a) − E) dX −1 ≡ 1 . g(a, E) (2.57) Величина g(a, E) – площадь гиперповерхности в фазовом пространстве X , выделяемой условием постоянства энергии (2.53). Используя это обозначение, выражение (2.55) для функции распределения можно записать в виде f (X, a, E) = 1 δ (H(X, a) − E) . g(a, E) (2.58) Это выражение называют микроканоническим распределением Гиббса для классических систем. Покажем, что результат (2.58) отвечает условию равновероятности всех возможных микросостояний в случае, когда значение энергии системы фиксировано не точно, а с неопределенностью ΔE . Иными словами, вместо строгого равенства (2.53) выполняются неравенства E ≤ H(X, a) ≤ E + ΔE. 50 (2.59) Используем свойство δ -функции b a ⎧ ⎪ ⎪ ⎪ ⎨ δ(x − x )dx = ⎪ ⎪ ⎪ ⎩ 1, a ≤ x ≤ b, (2.60) 0, x < a, x > b и теорему о среднем. Тогда с помощью выражения (2.55) получим следующее равенство: δ (H(X, a) − E ) dE ≡ f (X, a, E)ΔE = E≤E ≤E+ΔE ⎧ ⎪ ⎪ ⎪ ⎨ =⎪ ⎪ ⎪ ⎩ C, E ≤ H(X, a) ≤ E + ΔE, (2.61) 0, H(X, a) < E, H(X, a) > E + ΔE. Отсюда следует, что функция f (X, a, E)ΔE постоянна (не зависит от X ). Напомним, что величина C определяется выражением (2.57). Используя полученные выражения для функции распределения f (X, a, E) , можно найти функции распределения значений любой функции динамических переменных A(X) : f (A, a, E) = δ (A − A(X)) · f (X, a, E)dX = 1 = δ (A − A(X)) · δ (H(X, a) − E) dX. g(a, E) (2.62) Из этого определения следует, что функция f (A) положительна при всех значениях A и f (A, a, E)dA = 1. (2.63) При получении этого условия из (2.62) использовано равенство (2.57). Если в качестве A(X) выбрать функцию Гамильтона, т. е. A(X) = = H(X) , то функция распределения значений H(X) (а не значений X ) согласно (2.62) имеет вид f (H, a, E) = δ (H − E) (2.64) и, следовательно, отлична от нуля лишь при одном-единственном значении H = E . 51 Рассмотрим микроканоническое распределение для квантовых систем. Обозначим диагональные элементы матрицы плотности ρnn через wn , которые для равновесного состояния от времени не зависят. Через n обозначен полный набор квантовых чисел, характеризующих микроскопическое состояние макроскопической системы. Через En обозначим соответствующие возможные значения энергии системы. Предполагается, что они найдены при решении стационарного уравнения Шредингера для волновой функции ψ(q, t) рассматриваемой системы N -частиц. Энергия изолированной системы E = E0 = const . Это распределение можно записать по аналогии с классическим микроканоническим распределением Гиббса (2.58), если вместо δ -функции использовать символ Кронекера: wn (a, N, E) = Здесь функция ⎧ ⎪ ⎪ ⎪ ⎨ δEn −E = ⎪ ⎪ ⎪ ⎩ 1 δE −E . g(a, N, E) n 1, En = E, 0, En = E. (2.65) (2.66) Величина g определяется выражением, аналогичным (2.57): g(a, N, E) = n δEn −E . (2.67) Из этого определения следует, что величина g(a, N, E) – число микросостояний с заданным значением энергии E (а также при заданных a , N ). Величину g называют статистическим весом или кратностью вырождения. Из выражения (2.65) следует, что все состояния, удовлетворяющие условию En = E, (2.68) имеют одинаковую вероятность, равную g −1 (a, N, E) . Таким образом, в основе квантового микроканонического распределения Гиббса лежит предположение о равной вероятности всех микросостояний, допускаемых условием En = E . 52 2.7 Статистическое определение энтропии Перейдем к установлению функций распределений для равновесных систем, когда их состояния задаются термодинамическими параметрами. Это предполагает, что функции распределения должны быть также представлены через эти величины. Чтобы решить эту задачу, необходимо в какой-либо форме установить взаимосвязь между статистической механикой и термодинамикой. Отправным пунктом различных обсуждений по этому вопросу является выражение (формула Больцмана) S = k ln W, (2.69) где S – энтропия системы, т. е. термодинамическая величина, W – число состояний, в которых может находиться система в некоторых заданных условиях, k – коэффициент пропорциональности (здесь k полагается равным постоянной Больцмана). Очевидно, что для случая изолированных систем, рассмотренных в предыдущем параграфе, следует полагать W ≡ g(E). (2.70) Используя (2.61), можно обосновать переход от выражения (2.69) к более общему выражению для энтропии S = −k ln f (X) · f (X)dX для классических систем и S = −k n ln wn · wn (2.71) (2.72) для квантовых систем, где f (X) и wn – соответствующие функции распределения. Выражения (2.71) и (2.72) в литературе часто называют энтропией по Гиббсу. Покажем, что ln W обладает свойствами, характерными для энтропии системы. Рассмотрим две макроскопические системы C1 и C2 , которым приписываем энергию E1 и E2 соответственно. Будем считать, что энергия принимает дискретные значения, разделенные интервалами δE . Однако этот интервал достаточно велик, чтобы в нем уместилось большое число состояний. Обозначим через W1 (E1 ) число состояний C1 в интервале энергий E1 + δE1 , а через W2 (E2 ) – число состояний C2 в интервале энергий E2 + δE2 . Считаем, что системы находятся в тепловом контакте, а внешние параметры фиксированы. Полная энергия составной системы C : E = E1 + E2 постоянна, и в целом она находится 53 в равновесии. Какова вероятность P (E1 ) того, что энергия системы C1 равна данному значению энергии E1 , т. е. лежит между E и E + δE ? Еe определим выражением P (E1 ) = W1∗ (E1 ) = const · W1∗ (E1 ), Wп (2.73) где Wп – полное число доступных состояний для C , W1∗ (E1 ) – полное число доступных состояний для C , при которых энергия подсистемы C1 равна E1 . При записи этого выражения использовали принцип равной вероятности. Величину W1∗ (E1 ) можно выразить через число состояний, доступных системам C1 и C2 W1∗ (E1 ) = W1 (E1 ) · W2 (E2 ) = W1 (E1 ) · W2 (E − E1 ). (2.74) Тогда вероятность того, что система C1 имеет энергию E1 , равна P (E1 ) = const W1 (E1 )W2 (E − E1 ). (2.75) Для большинства реальных систем W1 (E1 ) и W2 (E2 ) – быстро возрастающие функции энергии. Тогда выражения для P (E1 ) и W1 (E1 ) – быстро возрастающие функции, а выражение для W2 (E − E1 ) – быстро убывающая функция энергии. В результате вероятность P (E1 ) должна иметь максимум при некотором значении энергии E1 . Вместо функции P (E1 ) удобно рассматривать ее логарифм ln P (E1 ) = ln const + ln W1 (E1 ) + ln W2 (E2 ). (2.76) Экстремальное значение энергии E1 найдем из условия ∂ ln P 1 ∂P = = 0. ∂E1 P ∂E1 (2.77) Это соотношение представляем в виде ∂ ln W1 (E1 ) ∂ ln W2 (E2 ) − =0 ∂E1 ∂E2 (2.78) или ∂ ln W1 (E1 ) ∂ ln W2 (E2 ) = = β, ∂E1 ∂E2 где параметр β имеет размерность обратной энергии. 54 (2.79) Если считать, что внешние параметры системы фиксированы, как это и предполагалось, то условием равновесного состояния является равенство температур, т. е. T1 = T2 (см. п. 1.6.). Тогда из термодинамиче∂E следует, что S1 = k ln W1 и ского определения температуры T = ∂S S2 = k ln W2 . Соотношение S = k ln W будет справедливо для любого термодинамического объекта, находящегося в среде в равновесных условиях. 2.8 Каноническое распределение Теперь рассмотрим закрытую систему (см. п. 1.1), основное термодинамическое равенство для которой записывается в виде dE = T dS − Ada. (2.80) Будем учитывать, что энергия системы испытывает случайные изменения. Однако температура T системы остается постоянной ( T = const ). Такая ситуация возможна лишь в том случае, когда рассматриваемая система является малой подсистемой большого объекта (окружающей среды), находящегося в равновесных условиях. Считаем, что составная система рассматривается как изолированная. Тогда для нее используем микроканоническое распределение f (X1 , X2 , E) = Cδ[H(X1 ) + H(X2 ) + Hвз (X1 , X2 ) − E] и f (X1 , X2 , E)dX1 dX2 = 1, (2.81) (2.82) где X1 , X2 – динамические переменные исследуемой системы и окружающей среды соответственно, Hвз (X1 , X2 ) – энергия взаимодействия между системой и окружающей средой, E – полная энергия составной системы. Для упрощения записи в выражении для f (X1 , X2 , E) опущены зависимости от внешних параметров, которые в последующем будут учтены.Положим H(X1 ) , H(X2 ) всегда гораздо большими, чем Hвз (X1 , X2 ) . Тогда для искомой функции распределения имеем f (X1 ) = f (X1 , X2 , E)dX2 . 55 (2.83) Учитывая постоянство температуры исследуемой системы, следует считать, что всегда выполняется H(X2 ) H(X1 ) . В этом случае получаем f (X1 ) = C δ [H(X2 ) − E] dX2 = C δ [H(X2 ) − E] g(E2 )dE2 , (2.84) где в последнем выражении перешли к интегрированию по энергии. g(E2 ) = dX2 dE2 (2.85) – статистический вес для состояний окружающей среды. Теперь, учитывая рассматриваемую ситуацию E1 E2 , полагаем полную энергию системы E равной энергии окружающей среды E2 , т. е. E2 = E = const . В этом случае величину g(E2 ) , которая представляет полное число состояний окружающей среды, следует рассматривать фактически как постоянную, и для f (X1 ) получаем f (X1 ) = Cg(E − E1 ), (2.86) где интеграл от δ функции равен единице, а энергия E2 = E − E1 , где E1 – всегда существенно малая величина. Используем представление числа состояний системы через ее энтропию (см. п. 2.7).Тогда ⎡ ⎤ S(E − E1 ) ⎦ g(E − E1 ) = exp ⎣ . k (2.87) Осуществим разложение S(E − E1 ) = S(E) − E1 где ∂S + ..., ∂E (2.88) 1 1 ∂S = = . (2.89) ∂E a T2 T1 Равенство температур T1 = T2 является следствием равновесного состояния. При этом следует считать, что внешние параметры для системы a1 и окружающей среды a2 должны быть постоянными. Подстановка представленных выражений в функцию распределения (2.86) дает E1 f (X1 ) = C1 exp − . (2.90) kT1 56 Эта формула справедлива для любого закрытого объекта, находящегося при постоянных T и a в достаточно большой макроскопической среде. Опуская индекс, записываем в виде ⎡ ⎤ H(X, a) ⎦ f (X, a, T ) = const exp ⎣− , kT (2.91) (2.92) f (X, a, T )dX = 1, где случайная величина E1 заменена соответствующей функцией Гамильтона H(X, a) . Представим общую форму записи канонического распределения ⎡ ⎤ 1 H(X, a) ⎦ f (X, a, T ) = exp ⎣− , Z kT где Z= ⎡ (2.93) ⎤ H(X, a) ⎦ exp ⎣− dX kT (2.94) – статистический интеграл распределения. По аналогии записываем каноническое распределение для квантовых систем ⎡ ⎤ 1 E (a) n ⎦, (2.95) wn (a, T ) = exp ⎣− Z kT где ⎡ ⎤ E (a) n ⎦ Z = exp ⎣− (2.96) kT n – статистическая сумма распределения. 2.9 Обобщенное распределение Будем рассматривать открытую систему (см. п. 1.1), основное термодинамическое равенство для которой записывается в виде dE = T dS − Ada + μdN. (2.97) В качестве случайных величин в данном случае выступают энергия системы E и число частиц N . Функция Гамильтона будет определяться 57 зависимостью H = H(X, a, N ) , где в данном случае X и N – случайные. Положим, что величины a, T, μ являются заданными. Получим выражение для функции распределения f (X, N, a, T, μ) . Рассматриваем данную систему и окружающую среду как изолированную. Исходное микроканоническое распределение записываем в виде (индекс 1 – объект, индекс 2 – окружающая среда). f (X1 , X2 , N1 , N2 ) = Cδ [H(X1 , N1 ) + H(X2 , N2 ) − E] , (2.98) где N = N1 + N2 , E = E1 + E2 , т. е. полагаем, что отсутствует энергия взаимодействия между системой и окружающей средой Hвз (X1 , N1 , X2 , N2 ) = 0 . Постоянная C определяется условием нормировки: f (X1 , X2 , N1 , N2 ) dXN1 dXN2 = 1. (2.99) N1 N2 Искомую функцию распределения f (X1 , N1 ) представим через микроканоническое распределение f (X1 , N1 , X2 , N2 ) : f (X1 , N1 ) = f (X1 , X2 , N1 , N2 )dXN2 (2.100) Для рассматриваемой системы во всех случаях должно выполняться N1 << N2 и E1 << E2 . Это позволяет записать f (X1 , N1 ) = C =C δ [H (X2 , N2 ) − E] dXN2 = (2.101) δ [H (X2 , N2 ) − E] g (EN2 ) dEN2 , где dXN2 (2.102) dEN2 – статистический вес окружающей среды (для состояния E2 с числом частиц N2 ). Рассматривая g (EN2 ) как постоянную величину в данных условиях, записываем g (EN2 ) = g (E2 , N2 ) = f (X1 , N1 ) = C · g (E2 , N2 ) , (2.103) где интеграл от дельта-функции полагаем равным единице. Выражение для статистического веса можно записать в виде (см. п. 2.7) 1 g (E2 , N2 ) = exp S (E2 , N2 ) . k 58 (2.104) Энтропию S окружающей среды представляем выражением ∂S ∂S E1 − N1 + ..., (2.105) S2 (E − E1 , N − N1 ) = S (E, N ) − ∂E ∂N где ∂S ∂S 1 μ2 = , =− . (2.106) ∂E a,N T2 ∂N a,E T2 В состоянии равновесия должно выполняться T2 = T1 и μ2 = μ1 . Используя эти представления и вводя новую постоянную, получим μ1 N1 − EN1 f (X1 , N1 ) = const exp . kT (2.107) Эта формула справедлива для любого открытого объекта, находящегося при постоянных T, a, μ в достаточно большой макроскопической среде. Общая форма записи обобщенного распределения имеет вид ⎡ ⎤ μN − H (X, N, a) ⎦ 1 exp ⎣ f (X, N, a, T, μ) = Z0 kT (2.108) с учетом условия нормировки N где (2.109) f (X, N, a, T, μ)dXN = 1, ⎡ ⎤ μN − H (X, N, a) ⎦ exp ⎣ dXN (2.110) Z0 = kT N – статистическая сумма обобщенного распределения. Для квантовых систем распределение wn,N (a, T, μ) запишем по аналогии с классическим распределением ⎡ ⎤ 1 μN − En,N (a) ⎦ wn,N (a, T, μ) = exp ⎣ , Z0 kT (2.111) с учетом условия нормировки N где n (2.112) wn,N = 1, ⎡ ⎤ μN − En,N (a) ⎦ exp ⎣ Z0 = kT N n – статистическая сумма обобщенного распределения. 59 (2.113) 2.10 Соответствие квантовых и классических распределений При переходе от квантовых к классическим распределениям фор мально надо заменить суммирование . . . по возможным микросостоn яниям ( n ) квантовой системы на интегрирование ...dX по динамическим классическим переменным, например по координатам и импульсам частиц системы dX = dr1 dp1 ...drs dps , где s – число степеней свободы системы. Однако, чтобы результаты расчетов в последнем случае для тех или иных величин были правильными, необходимо учесть два фактора. 1. В квантовой механике для динамических переменных r и p существует соотношение (неопределенности) Δri · Δpi ≈ h , где h – постоянная Планка. Тогда это соотношение будет определять число состояний для классической системы следующим образом: n ... → ... dX , hs (2.114) где s – число степеней свободы. Для системы из N свободных частиц s = 3N . 2. Это относится к случаю однотипных частиц. В квантовой механике формулируется принцип тождественности, или принцип неразличимости одинаковых частиц. Когда для квантовых систем проводим сум мирование , то это означает, что проводится суммирование по всем n физически различным состояниям системы ni . Перестановка частиц по "своим" состояниям не приводит к появлению дополнительных состояний системы. В классической физике одинаковых частиц все частицы являются различными. В простейшем случае эту ситуацию можно пояснить следующим образом. Допустим, объект состоит из двух частиц – a и b . Частицы однотипны в том случае, если энергетический спектр состояний для них одинаков. Рассмотрим первую ситуацию. Частицы находятся в состояниях Ea,x1 и Eb,x2 , где xi = (ri , pi ) . Это микросостояние такой системы, энергия которой определяется Ea,x1 и Eb,x2 . Теперь переставим частицы по состояниям, т. е. будем иметь Ea,x2 и Eb,x1 . Это будет новое микросостояние системы, хотя физическое состояние – по энер60 гии – будет прежним. На таком простом примере создается впечатление, что перестановка частиц не влияет на конечное значение энергии системы. Однако это не так. Дело заключается в том, что все величины в статистической термодинамике получают в результате усреднения с помощью функций распределения по всевозможным состояниям системы. Это означает, что при интегрировании по состояниям N частиц необходимо учитывать расположение различимых частиц по возможным для них состояниям. Это приведет к тому, что число таких интегралов будет N ! (число перестановок из N частиц). Тогда с учетом принципа тождественности следует использовать условие перехода к результатам классической теории в виде n ... → 1 dX ... N ! h3N (2.115) В результате переход от статистической суммы канонического распределения к интегралу происходит следующим образом: Z= n ⎡ ⎤ En 1 H(X) ⎦ dX exp − → exp ⎣− . kT N! kT h3N (2.116) Для статистических сумм обобщенного распределения получаем → N N n 1 N! ⎡ ⎤ μN − En,N (a) ⎦ exp ⎣ → kT ⎡ exp ⎣ ⎤ μN − H(X, N, a) dXN ⎦ . kT h3N (2.117) 2.11 Дополнительные вопросы 1. Имеем частицу со спином, равным 1/2 , и магнитным моментом . Пространственное положение частиμ0 во внешнем магнитном поле B цы фиксировано. Магнитный момент частицы может быть направлен либо параллельно полю, либо антипараллельно. В первом случае энергия частицы равна −μ0 B , а во втором случае +μ0 B . Допустим, объект состоит из N таких частиц, взаимодействие между которыми отсутствует. Определить полное число возможных состояний системы при N = = 1, 2, 3, 4 . Допустим, при N = 4 энергия системы каким-либо образом 61 фиксирована и равна −2μ0 B . Установить число допустимых состояний в этом случае. Ответ: N = 1 , Wп = 2 ; N = 4 , Wп = 16W ; Wg (Em = −2μ0 B) = 4 ; энергетический спектр состоит из 5 уровней: gm1 = 1 , gm2 = 4 и т. д. 2. Для свободной классической частицы в объеме V полное число dW определяются вырасостояний Wп и статистический вес g(E) = dE 3 1 жениями Wп ∼ V E 2 и g(E) ∼ V E 2 . Получите выражение для Wп и g(E) системы из N свободных невзаимодействующих частиц. Согласны ли вы с утверждением, что для макроскопических тел число состояний "катастрофически" возрастает с увеличением энергии? 3. Частица массы m свободно перемещается в объеме V = L3 , где L – ребро куба. Собственные значения энергии частицы определяются выражением h̄2 π 2 2 En = (n1 + n22 + n23 ), 2 2mL gni = 1 , ni = 1, 2, . . . , n = (n1 , n2 , n3 ) . Допустим, такая модель находится в среде при T = 300 К. В каких состояниях по квантовым числам n следует ожидать нахождение частицы (для m взять массу электрона либо простейших молекул, L = 1 см)? Полагая, что при больших n энергетический спектр частицы можно считать непрерывным, получите выражение для статистического веса такой системы. Ответ: Wп = 18 ( 43 πn3 ) , где n = 1 L 2 πh̄ (2mE) ; 62 1 g(E) ∼ V E 2 .