Свободные и вынужденные колебания

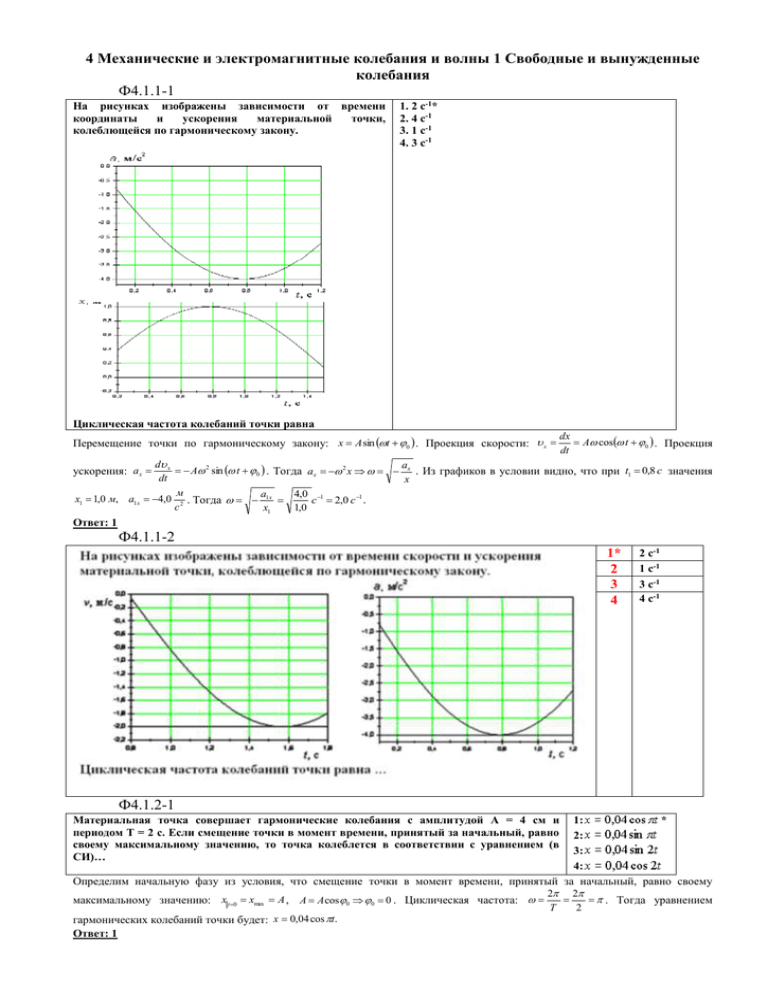
4 Механические и электромагнитные колебания и волны 1 Свободные и вынужденные
колебания
Ф4.1.1-1
На рисунках изображены зависимости от времени
координаты
и
ускорения
материальной
точки,
колеблющейся по гармоническому закону.
1. 2 с-1*
2. 4 с-1
3. 1 с-1
4. 3 с-1
Циклическая частота колебаний точки равна
Перемещение точки по гармоническому закону: x  A sin t  0  . Проекция скорости:  x 
dx
 A cos t   0  . Проекция
dt
d x
a
  A 2 sin  t  0  . Тогда ax   2 x     x . Из графиков в условии видно, что при t1  0,8 c значения
dt
x
м
a1x
4,0 1
1
x1  1,0 м, a1x  4,0 2 . Тогда   

с  2,0 с .
с
x1
1,0
ускорения: a x 
Ответ: 1
Ф4.1.1-2
1*
2
3
4
2 c-1
1 c-1
3 c-1
4 c-1
Ф4.1.2-1
Материальная точка совершает гармонические колебания с амплитудой А = 4 см и
периодом Т = 2 с. Если смещение точки в момент времени, принятый за начальный, равно
своему максимальному значению, то точка колеблется в соответствии с уравнением (в
СИ)…
1:
*
2:
3:
4:
Определим начальную фазу из условия, что смещение точки в момент времени, принятый за начальный, равно своему
2 2

  . Тогда уравнением
максимальному значению: x t 0  xmax  A , A  A cos 0  0  0 . Циклическая частота:  
гармонических колебаний точки будет: x  0,04 cos t.
Ответ: 1
T
2
Ф4.1.2-2
Материальная точка совершает гармонические колебания с амплитудой А = 4 см и
частотой = 2 Гц. Если смещение точки в момент времени, принятый за начальный,
равно нулю, то точка колеблется в соответствии с уравнением (в СИ)…
1:
2:
3:
4:
*
Циклическая частота:   2  2  2  4 . При t = 0, x t 0  A sin  t t 0  0 . Значит x  0,04 sin 4t .
Ответ: 1
Ф4.1.2-3
Материальная точка совершает гармонические колебания с амплитудой А = 4 см и
частотой = 2 Гц. Если смещение точки в момент времени, принятый за начальный,
равно своему максимальному значению, то точка колеблется в соответствии с
уравнением (в СИ)…
1:
*
2:
3:
4:
Определим начальную фазу из условия, что смещение точки в момент времени, принятый за начальный, равно своему
максимальному значению: x t 0  xmax  A , A  A cos 0  0  0 . Циклическая частота:   2  2  2  4 . Тогда уравнением
гармонических колебаний точки будет: x  0,04 cos 4t.
Ответ: 1
Ф4.1.2-4
Материальная точка совершает гармонические колебания с амплитудой А = 4 см и
периодом Т = 2 с. Если смещение точки в момент времени, принятый за начальный,
равно 2 см, то точка колеблется в соответствии с уравнением (в СИ)…
1:
*
2:
3:
4:
Циклическая частота:  

2 2
А



  . При t = 0, x t 0  A sin  0   0,02 , тогда  0  . Следовательно x  0,04 sin  t   .
6
T
2
2
6

Ответ: 1
Ф4.1.2-5
Материальная точка совершает гармонические колебания с амплитудой А = 4 см и
частотой = 2 Гц. Если смещение точки в момент времени, принятый за начальный,
равно 2 см, то точка колеблется в соответствии с уравнением (в СИ)…
1:
*
2:
3:
4:
Циклическая частота:   2  2  2  4 . При t = 0, x t 0  A cos 0 

А


 0,02 , тогда  0  . Следовательно x  0,04 cos 4t   .
3
2
3

Ответ: 1
Ф4.1.3-1
Уравнение движения пружинного маятника
1. вынужденных колебаний
2. свободных затухающих колебаний*
3. свободных незатухающих колебаний
является дифференциальным уравнением …
Дифференциальные уравнения движения пружинного маятника:
F0
F
d 2 x b dx k
cos  t или

 x  0 cos  t , где x – смещение колеблющегося тела из
m
dt 2 m dt m
m
k
положения равновесия; δ=b/m – коэффициент затухания, 0 
– собственная частота той же колебательной системы, F0 –
m
1) Вынужденные колебания: x  2 x  02 x 
амплитуда вынуждающей силы, k – коэффициент жёсткости пружины, m – масса тела.
d 2 x b dx k

 x  0.
dt 2 m dt m
2
d x k
3) Свободные незатухающие колебания: x  02 x  0 или 2  x  0 .
dt
m
2) Свободные затухающие колебания: x  2 x  02 x  0 или
Ответ: 2
Ф4.1.3-2
Уравнение движения пружинного маятника
1: свободных незатухающих колебаний*
2: свободных затухающих колебаний
3: вынужденных колебаний
является дифференциальным уравнением …
Дифференциальные уравнения движения пружинного маятника:
F0
F
d 2 x b dx k
cos  t или

 x  0 cos  t , где x – смещение колеблющегося тела из
m
dt 2 m dt m
m
k
положения равновесия; δ=b/m – коэффициент затухания, 0 
– собственная частота той же колебательной системы, F0 –
m
1) Вынужденные колебания: x  2 x  02 x 
амплитуда вынуждающей силы, k – коэффициент жёсткости пружины, m – масса тела.
d 2 x b dx k

 x  0.
dt 2 m dt m
d 2x k
3) Свободные незатухающие колебания: x  02 x  0 или 2  x  0 .
dt
m
2) Свободные затухающие колебания: x  2 x  02 x  0 или
Ответ: 1
Ф4.1.3-3
Уравнение движения пружинного маятника
1: вынужденных колебаний*
2: свободных затухающих колебаний
3: свободных незатухающих колебаний
является дифференциальным уравнением …
Дифференциальные уравнения движения пружинного маятника:
F0
F
d 2 x b dx k
cos  t или

 x  0 cos  t , где x – смещение колеблющегося тела из
m
dt 2 m dt m
m
k
положения равновесия; δ=b/m – коэффициент затухания, 0 
– собственная частота той же колебательной системы, F0 –
m
1) Вынужденные колебания: x  2 x  02 x 
амплитуда вынуждающей силы, k – коэффициент жёсткости пружины, m – масса тела.
d 2 x b dx k

 x  0.
dt 2 m dt m
d 2x k
3) Свободные незатухающие колебания: x  02 x  0 или 2  x  0 .
dt
m
2) Свободные затухающие колебания: x  2 x  02 x  0 или
Ответ: 1
Ф4.1.3-4
Свободные незатухающие колебания заряда
колебательном контуре описываются уравнением…
конденсатора
в
1:
*
2:
3:
Ответ: 1
Ф4.1.3-5
Свободные
затухающие
колебания
заряда
колебательном контуре описываются уравнением…
конденсатора
в
1:
*
2:
3:
Ответ: 1
Ф4.1.3-6
Вынужденные колебания заряда конденсатора в колебательном контуре
описываются уравнением…
1:
*
2:
3:
Ответ: 1
Ф4.1.4-1
Из графика колебаний материальной точки следует, что модуль скорости в момент времени
1. 9π см/с*
t
2. 0
3. 9 см/с
1
c равен …
3
4. 9π 3 см/с
2 2 1

c   с 1 . Проекция
T
2
1
времени t1  c величина
3
Из графика следует уравнение зависимости координаты x от времени   A sin  t , где А= 18 см,  
dx
 A cos  t . При одномерном случае    x  A cos  t .
dt


1 см
см
 A cos  t1  A cos  A cos  18   
 9
.
3
3
2 с
с
скорости
1   t t
1
x 
В
момент
Ответ: 1
Ф4.1.4-2
Материальная точка совершает гармонические колебания по закону
Максимальное значение скорости точки равно …
В рассматриваемом одномерном случае  max   x max 
.
1. π м/с
2. 0,1π м/с
3. 2π м/с
4. 0,2π м/с*
dx
2

м
 2
 0,3 
  sin 
t 
 0,2 .
dt max
3
3
4
с

 max
Ответ: 4
Ф4.1.5-1
При свободных колебаниях маятника максимальное значение
потенциальной энергии равно 10 Дж, максимальное значение
кинетической энергии равно 10 Дж. Полная механическая энергия …
1. изменяется в пределах от 0 до 10 Дж
2. не изменяется и равна 20 Дж
3. не изменяется и равна 10 Дж*
4. изменяется в пределах от 0 до 20 Дж
Поскольку максимальные значения кинетической и потенциальной энергий совпадают, то рассматриваются свободные
гармонические (незатухающие) колебания, при которых выполняется закон сохранения полной механической энергии. По
закону сохранения полной механической энергии максимальное значение кинетической энергии (10Дж) достигается при
минимальном значении потенциальной (0Дж), и наоборот. Следовательно, полная механическая энергия не изменяется и равна
10 Дж.
Ответ: 3
Ф4.1.5-2
Правильный ответ 4.
Ф4.1.6-1
Материальная точка совершает гармонические колебания с амплитудой А = 4 см и
периодом Т = 2 с. Если смещение точки в момент времени, принятый за начальный, равно
нулю, то точка колеблется в соответствии с уравнением (в СИ) …
1. x = 0,04 cos2t
2. x = 0,04 sin2t
3. x = 0,04 sinπt*
4. x = 0,04 cosπt
Поскольку по условию в начальный момент времени x0=0, то из предложенных ответов этому условию соответствует
тригонометрическая функция sin. Аргументом тригонометрической функции для гармонических колебаний в данном случае
2 2

  . Поэтому точка колеблется в соответствии с уравнением x  0,04 sin  t .
является ωt (поскольку φ0=0). Величина  
T
2
Ответ: 3
Ф4.1.7-1
На рисунке изображён график затухающих колебаний, где S – колеблющаяся величина,
описываемая уравнением
. Определите время релаксации τ (в с).
1. 1
2. 0,5
3. 2*
4. 3
I способ: По определению время релаксации τ – это время, за которое амплитуда уменьшается в е раз. Из графика видно, что в
начальный момент А0=2,7. Также из графика следует, что амплитуда уменьшается в е=2,7 раз через 2 с. Поэтому τ=2 с.
At 
 e Т , где A(t) и A(t+T) – амплитуды двух последовательных колебаний;
At  T 
At 
 T . Из теории известно выражение, связывающее логарифмический
логарифмический декремент затухания:   ln
At  T 
T
T
T
T
2T
2



c2c.
декремент затухания и время релаксации:   , откуда   
A0
A0
2,7

 ln At 
ln
ln
ln
At  T 
AT 
A2T 
1
II способ: По определению декремент затухания
Ответ: 3
Ф4.1.7-2
На рисунке изображен график затухающих колебаний, где S – колеблющаяся величина,
описываемая уравнением
. Определите коэффициент затухания .
I способ: Время релаксации τ=2 с, тогда коэффициент затухания  
1

1: 0,5*
2: 1
3: 2
4: 2,7
 0,5 с 1 .
At 
 e Т , где A(t) и A(t+T) – амплитуды двух последовательных колебаний;
At  T 
At 
A0
A0
2,7
ln
ln
ln
ln
At 





A
t

T
A
T
A
2T 
1  0,5 с 1 .
логарифмический декремент затухания:   ln
 T . Тогда  



At  T 
T
T
2T
2
II способ: Декремент затухания:
Ответ: 1
Ф4.1.7-3
1*
2
3
4
увеличится в 2 раза
уменьшится в 2 раза
увеличится в 4 раза
уменьшится в 4 раза
Ф4.1.8-1
Правильный ответ 3.
Ф4.1.9-1
Из
перечисленных
поперечными являются…
волн
1. звуковые волны в газах
2. радиоволны*
3. упругие волны в твёрдом теле, которое может растягиваться и сжиматься
4. световые волны в вакууме*
5. ультразвуковые волны в жидкостях
6. упругие волны в твёрдом теле, в котором возможны деформации*
Радиоволны и световые волны являются электромагнитными, следовательно – поперечными. В твердых телах возникают
продольные и поперечные волны. В жидкостях и газах только продольные волны. Продольная волна возникает, когда есть
деформация сжатия или растяжения.
Ответы: 2, 4, 6
Ф4.1.10-1
На рисунке показан «моментальный снимок» плоской волны,
распространяющейся в направлении у от источника, частота колебаний
которого равна 1 кГц.
1.
2.
3.
*
4.
Уравнение волны имеет вид…
Общий вид уравнения волны (с учётом представленного графика) x  A sin( t  ку  0 ) . Из графика следует, что φ0=0. По
условию задания собственная частота ν=1кГц=103 Гц. Отсюда циклическая частота ω=2πν=2.103π рад.Гц, что соответствует
2
2 рад
рад
ответам 3 и 4. Волновое число k 
. Из графика видно, что λ=0,2 м. Тогда k 
, что соответствует ответу 3
 10

( 2 10 3  0,005
Ответ: 3
рад
рад
).
 10
м
м
0,2 м
м