Обратный Комптон

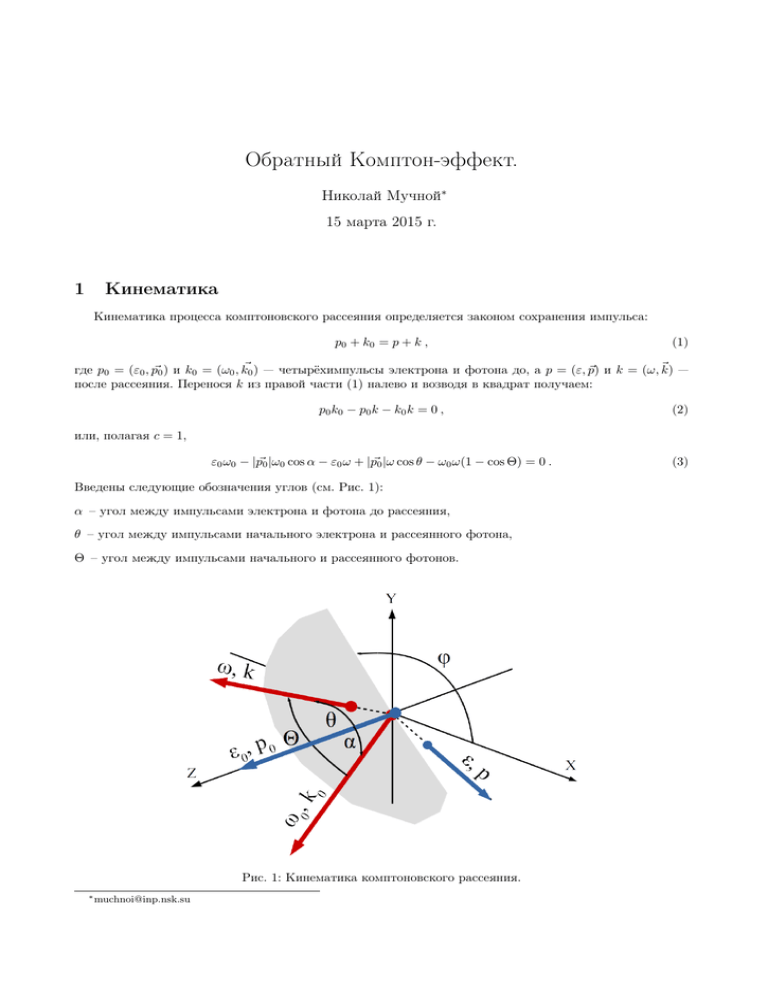
Обратный Комптон-эффект.
Николай Мучной∗
15 марта 2015 г.
1
Кинематика
Кинематика процесса комптоновского рассеяния определяется законом сохранения импульса:
p0 + k0 = p + k ,
(1)
где p0 = (ε0 , p~0 ) и k0 = (ω0 , k~0 ) — четырёхимпульсы электрона и фотона до, а p = (ε, p~) и k = (ω, ~k) —
после рассеяния. Перенося k из правой части (1) налево и возводя в квадрат получаем:
p0 k0 − p0 k − k0 k = 0 ,
(2)
ε0 ω0 − |p~0 |ω0 cos α − ε0 ω + |p~0 |ω cos θ − ω0 ω(1 − cos Θ) = 0 .
(3)
или, полагая c = 1,
Введены следующие обозначения углов (см. Рис. 1):
α – угол между импульсами электрона и фотона до рассеяния,
θ – угол между импульсами начального электрона и рассеянного фотона,
Θ – угол между импульсами начального и рассеянного фотонов.
Рис. 1: Кинематика комптоновского рассеяния.
∗ muchnoi@inp.nsk.su
Из (3) получаем выражение для энергии рассеянного фотона:
ω = ω0
1 − β cos α
,
ω0
1 − β cos θ +
(1 − cos Θ)
ε0
(4)
где β – скорость электрона в единицах c. При рассеянии на покоящемся электроне β = 0 и из (4) получаем
классическую формулу Комптона:
1
ω = ω0
.
(5)
ω0
1+
(1 − cos Θ)
m
Разместим систему координат так, чтобы ось Z совпадала с направлением импульса начального электрона а ось X лежала в плоскости рассеяния электрона (Рис. 1). Угол Θ можно выразить через α, θ и
азимутальный угол ϕ между плоскостями рассеяния электрона и фотона:
cos Θ = cos α cos θ + sin α sin θ cos ϕ .
(6)
В частном случае ϕ = 0 плоскости рассеяния обеих частиц совпадают и Θ = θ − α (Рис. 2). Важно, что
если α = π, то все импульсы всегда лежат в одной плоскости и Θ = θ − π.
Рис. 2: Кинематика комптоновского рассеяния в “плоском” случае ϕ = 0.
Перейдем в систему покоя электрона (СПЭ), движущегося вдоль оси Z. В СПЭ энергию и импульс
фотона получим из преобразований Лоренца1 :
ω0∗ = γω0 (1 − β cos α) ' 2γω0 sin2 (α/2),
kk∗ =
∗
k⊥
γω0 (cos α − β) '
=
−2γω0 sin2 (α/2),
(7)
ω0 sin α,
p
где γ = 1/ 1 − β 2 = ε0 /m. Приближение в (7) соответствует ультра-релятивистскому случаю β ' 1.
В СПЭ угол α∗ между импульсами электрона и фотона до рассеяния определяется выражением (8),
причем α∗ ' π если γ · tg(α/2) 1.
α∗ = π − arctg
1
1
∗
k⊥
sin α 1
' π − arctg
'π−
' π.
∗
|kk |
2γ sin2 (α/2)
γ · tg(α/2)
Преобразования Лоренца: E 0 = γ(E − vpz ),
p0z = γ(pz − vE/c2 ),
2
p0x = px ,
p0y = py .
(8)
Рис. 3: Кинематика комптоновского рассеяния в системе покоя электрона.
Кинематика рассеяния в СПЭ описывается формулой (5) и представлена на Рис. 3 (α∗ = π):
ω ∗ = ω0∗
1
1
= ω0∗
∗
ω0∗
ω
1+
(1 − cos Θ∗ )
1 + 0 (1 + cos θ∗ )
m
m
(9)
В лабораторной системе отсчета (ЛСО) получим:
ω = γω ∗ (1 + β cos θ∗ ) = γω ∗ (1 − β cos Θ∗ )
kk =
γω ∗ (β + cos θ∗ ) =
k⊥ =
∗
γω ∗ (β − cos Θ∗ )
∗
∗
ω sin θ =
(10)
∗
ω sin Θ
Угол θ между импульсами начального электрона и рассеянного фотона в ЛСО (для β = 1):
tgθ =
1 sin θ∗
1 θ∗
1
k⊥
'
= tg =
∗
kk
γ 1 + cos θ
γ 2
γtg(Θ∗ /2)
(11)
В релятивистском случае tgθ ' θ и, вводя новую переменную η = γθ , получим:
Θ∗ =
cos Θ∗ =
1 − cos Θ∗ =
ω0∗
1
η
η2 − 1
η2 + 1
2
2
η +1
2 · arctg
(12)
Запишем зависимость энергии рассеянного фотона в ЛСО (ω) от η, подставив (1 − cos Θ∗ ) из (12) и
из (7) в выражение для ω из (10). Получим:
ω(η) = ε0
κ
4ε0 ω0
, где κ =
sin2 (α/2) .
2
1+κ+η
m2
(13)
Максимальная энергия у фотона получается когда η = 0. Соответственно, (13) можно записать и так:
ω(η) =
ωmax
κ
, где ωmax = ε0
1 + (θ/θc )2
1+κ
, а θc =
1√
1+κ .
γ
(14)
Параметр θc определяет характерный угол рассеяния фотонов. Заметим, что выражения (13) и (14)
несложно получить непосредственно из уравнения (4). Связь между углом рассеяния фотона в СПЭ
(Θ∗ ) и его энергией в ЛСО (ω) получим, подставив ω ∗ из (9) в выражение для ω из (10):
cos Θ∗ =
ε0 − ω(1 + 2/κ)
u
ω
ω
ε0 − ε
= 1 − 2 , где u =
= =
.
ε0 − ω
κ
ε0 − ω
ε
ε
(15)
Параметр u максимален, когда Θ∗ = π: umax = κ. Зависимость от угла рассеяния: u(η) = κ/(1 + η 2 ).
3
2
Рассеяние без учета поляризации
Сечение комптоновского рассеяния определяется формулой Клейна-Нишины. Сохраняя введенные в
предыдущем разделе обозначения, запишем дифференциальное сечение в СПЭ2 :
dσ =
ω∗
re2 ω ∗ 2 ω0∗
+ ∗ − sin2 Θ∗ dΩ∗ ,
∗
∗
2 ω0
ω
ω0
(16)
где re – классический радиус электрона, dΩ∗ = sin Θ∗ dΘ∗ dϕ. Найдем вид сечения в ЛСО. Из выражений
(7, 9, 12) следует, что
1 + η2
ω∗
V
=
=
,
(17)
ω0∗
1 + η2 + κ
K
где V = 1 + η 2 и K = 1 + η 2 + κ – безразмерные параметры. Как следует из (12):
2η
,
V
p
sin Θ∗ =
1 − cos2 Θ∗ =
η2 − 1 dη =
dΘ∗ = d arccos 2
η +1
2
dη ,
V
4η
sin Θ∗ dΘ∗ = − 2 dη .
V
−
(18)
Проинтегрировав по ϕ, запишем конечный результат:
dσ = 4πre2
η V
K
4η 2 +
−
dη .
K2 K
V
V2
(19)
Выразим сечение через энергию рассеянного фотона. Из (12) и (15) получим связь между η и u:
η2 − 1
u
=1−2 .
η2 + 1
κ
Запишем результаты промежуточных вычислений:
η2 =
κ
− 1;
u
V =
κ
;
u
K=
κ
+ κ;
u
dη =
κ
2u2
p
κ/u − 1
du .
Подставляя все это в (19) получим:
dσ =
i
2πre2 h
u2
uu
2+
+4
− 1 du .
2
κ(1 + u)
1+u
κ κ
(20)
С учетом того, что du/dω = ε0 /(ε0 − ω)2 , а (1 + u)2 = (ε0 /(ε0 − ω))2 , получаем искомое сечение:
dσ =
3
i
2πre2 h
u2
uu
2+
+4
− 1 dω .
κε0
1+u
κ κ
(21)
Поляризационные эффекты
Поляризация исходного излучения описывается вектором Стокса ξ~ = [ξ0 , ξ1 , ξ2 , ξ3 ]. Параметры Стокса
определяются следующим образом:
ξ0 =
Ex2 + Ey2 ,
ξ1 =
Ex2 − Ey2 ,
ξ2 =
2Ex Ey cos δ ,
ξ3 =
2Ex Ey sin δ ,
(22)
где Ex и Ey – ортогональные компоненты амплитуд напряженностей электрического поля электромагнитной волны в выбранной системе координат xy, δ – разность фаз между ними (волна распространяется
2 иногда
сечение записывают по-другому, используя равенство
4
∗
ω0
ω∗
+
ω∗
∗
ω0
− 2 = (ω0∗ − ω ∗ )(1 − cos Θ∗ )
вдоль оси z). Для нормировки положим ξ0 = 1. В общем случае интенсивность света складывается из
трех компонент: линейно-поляризованной, циркулярно-поляризованной
и неполяризованного света. Стеp
пень линейной поляризации определяется как ξ12 + ξ22 , а ее ориентация – азимутальным углом φ. Если
ξ1 = 1 (Ex = 1) – свет 100% линейно поляризован
вдоль оси x (φ = 0), если ξ1 = −1 (Ey = 1) – вдоль
√
оси y (φ = π/2). Если ξ2 = 1 (Ex = Ey =√1/ 2, δ = 0) – свет 100% линейно поляризован в направлении
φ = π/4, если ξ2 = −1 (Ex = Ey = 1/ 2, δ = π) – в направлении
φ = −π/4. Степень циркулярной
√
поляризации определяется параметром ξ3 . Если Ex = Ey = 1/ 2 а δ = ±π/2 то ξ3 = ∓1. Знак параметра ξ3 определяет направление вращения вектора электрического поля (спиральность). Величина
p
ξ12 + ξ22 + ξ32 определяет полную степень поляризации света.
Поляризация электронного пучка определяется усредненным направлением спина электронов в вы~
бранной системе
q прямоугольных координат ζ = [ζx , ζy , ζz ] (см. Рис. 1), причем полная степень поляризации пучка
3.1
ζx2 + ζy2 + ζz2 ∈ [0, 1].
Рассеяние поляризованного излучения
Продолжая использовать переменные с индексом (∗ ) для описания переменных в СПЭ, запишем
сечение рассеяния поляризованного фотона поляризованным электроном:
2 ∗ 2
~ ζ)
~ = dσ(ξ)
~ + re ω
dσ(ξ,
ξ3 (f~ · ζ~ )dΩ∗ ,
2 ω0∗
(23)
~ не зависит от поляризации электронов:
где dσ(ξ)
~ =
dσ(ξ)
ω∗
re2 ω ∗ 2 ω0∗
2 ∗
+
−
(1
−
ξ
)
sin
Θ
dΩ∗ .
1
2 ω0∗
ω∗
ω0∗
(24)
Вектор f~ в уравнении (23) определяется кинематикой рассеяния:
1
f~ = − (1 − cos Θ∗ )(k~0∗ cos Θ∗ + k~∗ ).
m
(25)
Сечение (23) отличается от (24) только при наличии у фотона циркулярной поляризации, а у электрона – отличной от нуля проекции среднего спина на плоскость рассеяния. Сечение (24) отличается от
“неполяризованного” сечения (19) только при наличии у начальных p
фотонов линейной поляризации.
Вместо параметра ξ1 удобно использовать пару параметров ξ ∗ = ξ12 + ξ22 и φ∗ , определяющих соответственно полную степень линейной поляризации (лазерных) фотонов и ориентацию плоскости линейной поляризации света относительно направления ϕ = 0 в выбранной системе координат:
ξ1 = ξ ∗ cos 2(ϕ − φ∗ ) .
Перепишем сечение (24) в ЛСО с использованием введенных раннее переменных η, K, V, u:
dσ =
dσ =
i
η hV
K
4η 2 ∗
∗
+
−
1
−
ξ
cos(2(ϕ
−
φ
))
dϕ dη,
K2 K
V
V2
h
i
re2
u2
uu
2+
+4
− 1 1 − ξ ∗ cos(2(ϕ − φ∗ )) dϕ du.
2
κ(1 + u)
1+u
κ κ
2re2
(26)
В соответствии с Рис. 4 найдем проекции вектора f~ на оси Z, X, Y :
fZ =
fX =
fY =
1 − cos Θ∗ ∗
V κ(η 2 − 1)
(ω0 + ω ∗ ) cos Θ∗ =
1+
,
m
K
V2
2κη
1 − cos Θ∗ ∗
ω sin Θ∗ cos ϕ =
−
cos ϕ ,
−
m
KV
∗
1 − cos Θ ∗
2κη
−
ω sin Θ∗ sin ϕ =
−
sin ϕ .
m
KV
(27)
При выводе формул (27) использовалось, что ω0∗ = κm/2, а ω ∗ = ω0∗ · V /K. При рассеянии циркулярно
поляризованного света на электроне, спин которого направлен вдоль собственного импульса (лежит на
оси Z – продольная поляризация), поляризационная добавка к сечению в ЛСО определяется формулами
5
Рис. 4: К определению суммы k~0∗ cos Θ∗ + k~∗ .
(28). Поскольку в этом случае сечение не зависит от азимутального угла, произведено интегрирование
по ϕ.
V κη(η 2 − 1)
dσk = 4πre2 ξ3 ζk 1 +
dη , (a)
K
K 2V 2
u(u + 2)(κ − 2u)
du ,
(b)
dσk = 2πre2 ξ3 ζk
(28)
κ2 (u + 1)3
u(u + 2)(κ − 2u) dω
dσk = 2πre2 ξ3 ζk
·
. (c)
κ2 (u + 1)
ε0
35
ξ₃×ζ∥= 0
ξ₃×ζ∥= 1
ξ₃×ζ∥= -1
30
dσ, mbarn / GeV
25
20
15
10
5
0
0
5
10
15
20
25
30
ω, GeV
Рис. 5: Сечения рассеяния фотона (ф-лы 20 и 28c) ω0 = 2 эВ на электроне ε0 = 50 ГэВ
При рассеянии циркулярно поляризованного света на электроне, спин которого направлен поперек
собственного импульса (поперечная поляризация), поляризационная добавка к сечению в ЛСО определяется формулой (29). Видно, что при интегрировании по ϕ эта добавка к сечению равна нулю и не
меняет зависимость сечения от энергии рассеянного фотона.
dσ⊥ =
dσ⊥ =
κη 2
−4re2 ξ3 ζ⊥
sin ϕ dϕ dη, (a)
V K3
p
u2 κ/u − 1
−2re2 ξ3 ζ⊥ 2
sin ϕ dϕ du. (b)
κ (1 + u)3
6
(29)