1.6. Свойства сложения векторов
advertisement
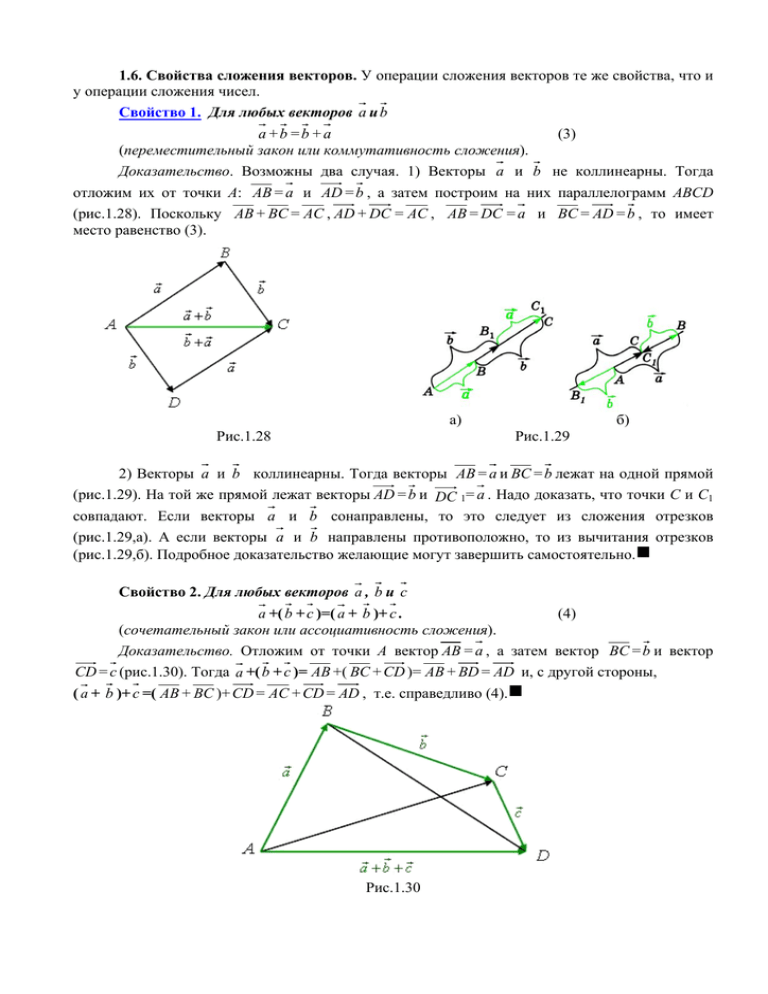
1.6. Свойства сложения векторов. У операции сложения векторов те же свойства, что и у операции сложения чисел. Свойство 1. Для любых векторов а и b а +b =b +а (3) (переместительный закон или коммутативность сложения). Доказательство. Возможны два случая. 1) Векторы а и b не коллинеарны. Тогда отложим их от точки А: AB = а и AD = b , а затем построим на них параллелограмм ABCD (рис.1.28). Поскольку AB + BC = AC , AD + DC = AC , AB = DC = а и BC = AD = b , то имеет место равенство (3). а) Рис.1.28 б) Рис.1.29 2) Векторы а и b коллинеарны. Тогда векторы AB = а и BC = b лежат на одной прямой (рис.1.29). На той же прямой лежат векторы AD = b и DC 1= а . Надо доказать, что точки С и С1 совпадают. Если векторы а и b сонаправлены, то это следует из сложения отрезков (рис.1.29,а). А если векторы а и b направлены противоположно, то из вычитания отрезков (рис.1.29,б). Подробное доказательство желающие могут завершить самостоятельно.g Свойство 2. Для любых векторов а , b и с (4) а +( b + с )=( а + b )+ с . (сочетательный закон или ассоциативность сложения). Доказательство. Отложим от точки А вектор AB = а , а затем вектор BC = b и вектор CD = с (рис.1.30). Тогда а +( b + с )= AB +( BC + CD )= AB + BD = AD и, с другой стороны, ( а + b )+ с =( AB + BC )+ CD = AC + CD = AD , т.е. справедливо (4).g Рис.1.30 Пользуясь этим законом, можно группировать слагаемые при любом их числе, т.е. заключать в скобки любым образом. Поэтому суммы векторов пишут, никак не объединяя слагаемые скобками: а + b + с , а + b + с + d и т.д. Из сочетательного и переместительного законов следует, что, складывая любое число векторов, можно как угодно переставлять и группировать слагаемые (так же как и числа). Часто это значительно облегчает сложение при числе слагаемых, большем двух. Чтобы сложить несколько векторов, например векторы а , b , с , d , удобно построить векторную ломаную (рис.1.31). Эта ломаная состоит из направленных отрезков AB = а , BC = b , CD = с , DE = d . Вектор AE , идущий от начала ломаной ABCDЕ в ее конец, и является суммой: AE = а + b + с + d . Рис.1.31 Рис.1.32 Если ломаная получилась замкнутой, то сумма векторов равна нуль-вектору (рис.1.32). Отметим еще очевидное свойство нуль-вектора: Свойство 3. а + 0 = а . Динамические модели "1_07_Коммутативность сложения векторов" Вопросы для самоконтроля 1. В чем состоит переместительный закон сложения векторов? Как его еще называют? 2. В чем состоит сочетательный закон сложения векторов? Как его еще называют? 3. Как получить сумму векторной ломаной? Когда эта сумма равна нулю? Задачи Рисуем. 6.1. Нарисуйте треугольник АВС. Нарисуйте векторы: а) AB + AC + BC ; б) AC + ВА + BC ; в) СА + СВ + ВА ; г) ВА + СВ + AC . 6.2. Нарисуйте четырехугольник ABCD. Нарисуйте векторы: а) AB + BC + CD ; б) ВА + AD + DC ; в) DA + CD + AB ; г) AC + BD + СВ ; д) BC + BD + CD ; е) AB + DB + СВ ; ж) AB + СА + BD + DC . 6.3. От одной точки отложены три вектора равной длины. Один из этих векторов равен сумме двух других. Нарисуйте эти векторы. Находим величину. 6.4. Из одной точки выходят три вектора, длина каждого равна а. Они образуют между собой углы 120о. Чему равна длина их суммы? В какой известной басне А.И.Крылова описана аналогичная ситуация? 6.5. Дан единичный куб ABCDA1B1C1D1. Чему равна длина вектора: а) AB + CD + А1С1 ; б) СА + DB + А1С1 ; в) А1С1 + CD 1+ D1 A ?


