3.2. Кратномасштабный анализ
advertisement
Введение в вейвлет-анализ
Кратко поясним, что такое вейвлет-преобразование и почему оно оказывается
необходимым, когда есть такие хорошо известные методы, как преобразование Фурье.
Оно обладает существенным недостатком: базисные функции такого разложения множество синусов и косинусов различных частот, которые отличны от нуля на всей
числовой прямой. Это приводит к двум основным недостаткам при анализе сигналов:
для получения информации даже об одной частоте требуется вся временная
информация, т.е даже будущее поведение сигнала должно быть заранее известно.
большинство реальных сигналов нестационарно и пики во временной области
сигнала дают вклад во всю частотную область.
Эффективность вейвлет-анализа в сравнении с преобразованием Фурье объясняется
большей информативностью первого из них, предоставляющего исследователям
дополнительную степень свободы для анализа в виде возможности видеть разложение
сигналов по компактным базисным функциям не только при различных масштабах
(частотах), но и при различных сдвигах по времени, что позволяет локализовать
временные особенности сигнала.
Таким образом, одномерное вейвлет-преобразование сигнала f(x) является двумерной
функцией:
где ядро Ψ называется вейвлетом, b - смещением, a - масштабом или шкалой.
Нормирующий коэффициент равен
~
где (ω) -- фурье-образ вейвлета Ψ. Условие
является условием существования вейвлета.
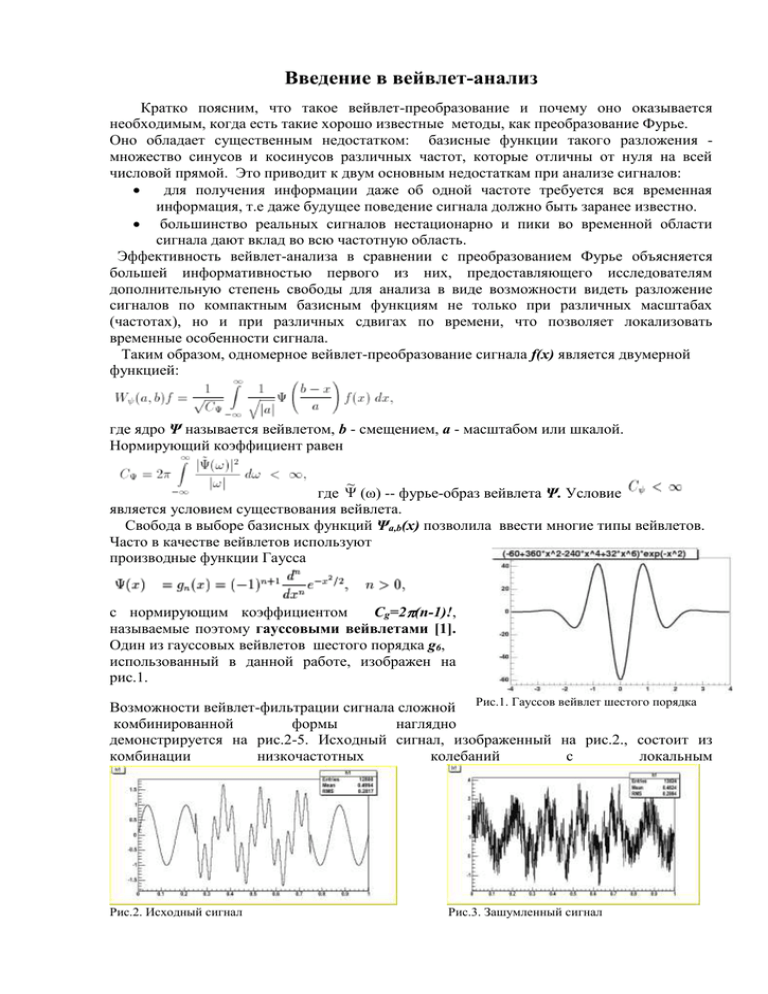
Свобода в выборе базисных функций Ψa,b(x) позволила ввести многие типы вейвлетов.
Часто в качестве вейвлетов используют
производные функции Гаусса
с нормирующим коэффициентом
Cg=2(n-1)!,
называемые поэтому гауссовыми вейвлетами [1].
Один из гауссовых вейвлетов шестого порядка g6,
использованный в данной работе, изображен на
рис.1.
Возможности вейвлет-фильтрации сигнала сложной Рис.1. Гауссов вейвлет шестого порядка
комбинированной
формы
наглядно
демонстрируется на рис.2-5. Исходный сигнал, изображенный на рис.2., состоит из
комбинации
низкочастотных
колебаний
с
локальным
Рис.2. Исходный сигнал
Рис.3. Зашумленный сигнал
высокочастотным пакетом. На рис.3 показан результат зашумления этого сигнала
гауссовым шумом с 20%-й амплитудой. Двумерный вейвлет-спектр результирующего
сигнала при применения гауссового вейвлета g2 показан на рис.4. Большие по значению
вейвлет-коэффициенты изображены точками большей светлости, меньшие – более
темными.
Рис.4 Вейвлет-спектр сигнала с рис.3.
По вертикали отложен масштаб (частота), по горизонтали – временной сдвиг.
Горизонтальные линии отмечают хорошо различимые области шумовых колебаний
(внизу) в средней области виден высокочастотный пакет, а выше – низкочастотная
составляющая сигнала. Используя частоты, можно легко разделить вейвлет-спектр на
шумовую, и низкочастотную части, а применив дополнительно пороговое обрезание по
амплитудам пикселей, можно выделить ту часть которая порождена высокочастотным
пакетом. Выполняя обратное преобразование, мы осуществим фильтрацию исходного
сигнала, представленного на рис.3, от шумов и отделение низкочастотной части сигнала
от высокочастотного пакета (см. рис.5.).
Рис.5
Отметим, что Фурье-анализ этого примера не позволил бы локализовать границы
высокочастотного пакета, а выдал бы только сведения о его частоте.
Следует также указать, что при практической реализации вейвлет-анализа на
компьютере непрерывное вейвлет-преобразование по необходимости должно быть
дискретизовано, причем умелая дискретизация с учетом как шага дискретности измерений
сигнала, так и конечности множества, на котором задан базисный вейвлет, дает
возможность значительно (на несколько порядков) ускорить вычисление полного набора
вейвлет-коэффициентов. Дискретность исходных данных явилась также поводом для
разработки многих типов дискретных вейвлетов, среди которых наиболее применимы
вейвлеты Добеши, обладающие рядом оптимальных свойств [2].
Дискретное вейвлет-преобразование
Казалось бы, что идеальный инструмент анализа сигналов любого вида получен. Но, к
сожалению, концепция непрерывного вейвлет- преобразования обладает своими
недостатками. Параметры в a и b формуле (5) меняются непрерывно, что приводит к
избыточному представлению спектра сигнала. В некоторых задачах это несомненно
является плюсом, кроме того благодаря своей избыточности спектры непрерывного
преобразования достаточно наглядны. Однако платой за эту избыточность является
сравнительно невысокая скорость выполнения преобразования, требующая вычисления
интегралов для каждого из значений обоих параметров a и b. Хотя в случае гауссовых
вейвлетов интегрирование может быть выполненно аналитически, тем не менее в общем
случае это не спасает от избыточности представления, и как правило соответственно
невысокой скорости его выполнения. Кроме того, поскольку на практике все сигналы, с
которыми имеют дело физики, и не только физики, имеют дискретную природу, то вопрос
о целесообразности применения масштаба вейвлета, покрывающего к примеру полторы
точки исходного сигнала остается открытым. Таким образом, мы видим, что более
употребительной при компьютерных вычислениях с реальными данными должны быть
дискретные вейвлет-преобразования.
Необходимая дискретизация значений a и b осуществляется следующим образом:
a a 0m , b na 0m ; m, n Z
(6)
Видно, что с увеличением масштаба увеличивается и размер сдвига функции, поскольку
интуитивно понятно, что при анализе с большим масштабом, более мелкие детали
игнорируются.
Дискретное вейвлет преобразование строится с помощью
кратномасштабного анализа (МА -- Multiresolution analysis), впервые описанного
Маллатом (Mallat).
Основная идея МА состоит в представлении сигнала в виде совокупности его
последовательных приближений. Теория кратномасштабного анализа относится к теории
функциональных пространств. Под кратномасштабным анализом понимается описание
пространства L2(R) через последовательность непересекающихся иерархически
вложенных подпространств Vm, объединение которых в пределе дает описываемое
пространство.
V
mZ
m
, Vm L2 ( R)
mZ
Эти пространства должны обладать следующим свойством: Для любой функции
f ( x) Vm принадлежащей подпространству, её сжатая версия должна принадлежать
подпространству f (2 x) Vm 1 . Еще одно необходимое свойство, что существует такая
функция ( x) V0 , сдвиги 0, n ( x ) ( x n), n Z которой образуют ортонормированный
базис пространства. Из этого вытекает, что набор m,n ( x) 2 m / 2 (2 m x n)
функций образует ортонормированный базис соответственно пространства Vm.
Следовательно, любая функция из L2(R) может быть представлена как предел к которому
стремятся ее аппроксимации fm(x) в пространствах Vm, т.е. как видно мы имеем
возможность анализа функции на различных масштабах. Фундаментальным, и до
некоторой степени удивительным выводом кратномасштабного анализа является факт
связи между вейвлетами и банком фильтров. Действительно:
( x) 0,0 V0 V1 ; 0,0 21 / 2 hn 1,n ( x) 2 hn (2 x n) (7)
n
n
Уравнение (7) показывает эту связь и называется масштабирующим уравнением. Вейвлетфунция возникает при рассмотрении дополнения одного из подпространств Vm до под
пространства Vm-1.
Vm-1=Vm Wm .
Базисную функцию обозначим через . Очевидно, что поскольку Wm содержится в Vm-1 ,
то можно представить как разложение.
m,n ( x) 2 ( m 1) / 2 g n (2 ( m1) x n)
n
Итак, для дискретных сигналов концепция ДВП состоит в следующем:
вместо
первоначального набора xi коэффициентов мы получаем совокупность наборов,
{{sn},{{dj,n}}} которые и являются вейвлет-преобразованием сигнала, причем в отличие от
избыточного спектра непрерывного преобразования, количество полученных
коэффициентов равно их количеству в исходном массиве данных. Коэффициенты s(j)n называются коэффициентами аппроксимации, а dj,n – деталями, соответствующими
уровню разложения j. В итоге дискретное вейвлет-разложение функции выглядит
следующим образом: (обозначения немного изменены для удобства)
N
2L
N
L
f ( xi ) s k L,k ( xi )
k 1
j 1
2j
d
k 1
j ,k ( xi )
jk
(8)
Соответственно, один шаг подобного преобразования выполняется путем свертки пары
фильтров, в соответствии с диаграммой.
Рис.13. Один шаг вейвлет-разложения.
При каждом шаге разложения, сглаженная версия сигнала, разлагается на новую, еще
более сглаженную версию. Каждый из массивов вполовину меньше предыдущего.
Итерируя эту процедуру, получаем разложение вида (8). Как уже упоминалось, выбор
вейвлет-функций, по которым будет произведено разложение в результате итерационной
процедуры, зависит от применяемых фильтров. Критериями для выбора фильтров и
Р
Рис.14 Схема вейвлет-разложения.
соответствующих им вейвлетов могут служить, например, желание получить разложение
по симметричным и ортогональным вейвлет-функциям. К сожалению, доказано, что все,
за исключением простейшего вейвлета Хаара, ортогональные наборы вейвлетов
несимметричны. Максимально симметричными из семейства ортогональных вейвлетов
являются так наз. койфлеты, но они для сохранения первых M моментов сигнала имеют
фильтр длиной в полтора раза больше, чем семейство вейвлетов Добечи (т.е. 3M вместо
2M, как у Добечи).
Разложение по вейвлет-пакетам
Для частотно-временного анализа существует другой вид разложения - в вейвлет-пакеты.
Главное отличие этого разложения в том, что на каждом шаге декомпозиции детали также
подвергаются последующему разло жению. В результате каждый слой разложения
покрывает примерно одинаковую часть фурье-спекра. Лучше всего пояснить разницу в
спектрах обычного дискретного и разложения по вейвлет пакетам на примере сигнала,
состоящего из суммы двух chirp-сигналов, т.е сигналов с меняющейся во времени
частотой.
Рис.15. Отчетливо видны составляющие сигнала.
Из диплома С.Дмитриевского
3. Вейвлет-анализ как метод решения задачи фильтрации и сглаживания сигнала
Вейвлеты являются сравнительно новым изобретением в прикладной математике.
Это название само по себе возникло около десятилетия тому назад. За последние десять
лет интерес к ним вырос взрывообразно. С одной стороны, концепция вейвлетов может
рассматриваться как синтез идей, возникших за последние двадцать или тридцать лет в
технике, физике и математике. Вследствие своего междисциплинарного происхождения,
вейвлеты представляются привлекательными для ученых и инженеров с самыми разными
научными интересами. С другой стороны, вейвлеты являются довольно простым
математическим инструментом с большим разнообразием возможностей для применения.
Они были успешно применены для анализа сигнала (звук, изображение) и в численном
анализе (быстрые алгоритмы для интегральных преобразований).
3.1. Вейвлет-преобразование. Вейвлет-преобразование является методом,
разбивающим данные, функции или операторы на составляющие с разными частотами,
каждая из которых затем изучается с разрешением, соответствующим выбранному
масштабу. Прототипы этой техники появились независимо в чистой математике (формула
обращения Кальдерона), физике (когерентные состояния для (a bx) -группы в квантовой
механике), технике (КЗ фильтры с точным восстановлением для цифровой обработки
сигнала, вейвлеты Морле для анализа сейсмических данных). Исследования последних
пяти лет показали высокую продуктивность синтеза этих различных подходов для всех
областей.
Вейвлет-преобразование одномерного сигнала состоит в его разложении по базису,
сконструированому из особым образом сформированной анализирующей функции
посредством масштабирования и переноса. Элементом базиса вейвлет-преобразования
является хорошо локализованная функция, быстро спадающая к нулю за пределами
небольшого интервала.
3.1.1. Непрерывное вейвлет-преобразование. Прямое вейвлет-преобразование
функции f (x ) имеет вид
1 / 2
t b
W (a, b) f a
(3.1)
dtf (t ) a .
Здесь параметры сдвига и сжатия a , b непрерывно меняются вдоль R , с ограничением
a 0 . Любая функция может быть восстановлена с помощью формулы обращения.
da db
f C1 2 f , a ,b a ,b ,
(3.2)
a
t b
a,b
2
, а , обозначает скалярное произведение в L .Функции
a
называются «вейвлетами», функцию иногда называют «материнским вейвлетом».
Постоянная C зависит только от и дается формулой
где a ,b (t ) a
1 / 2
2
C 2 d ~ ( )
1
,
(3.3)
где ~ – Фурье-образ функции (см. гл. 4).
Здесь требуется, чтобы C (в противном случае (3.2) не имеет смысла). Если функция из L1 ( R) (как раз такие случаи представляют интерес), то ~ является
непрерывным, тогда C может иметь конечное значение, только если ~ (0) 0 , т.е.
dt (t ) 0 .
Формула (3.2) может быть рассмотрена с двух точек зрения: (1) как способ
восстановления f , если известно ее вейвлет преобразование W f или (2) как способ
записи f в виде суперпозиции вейвлетов a,b , коэффициенты в этой суперпозиции точно
заданы через вейвлет-преобразование f .
Соответствие f (t ) W f (a, b) сопоставляет функции одной переменной функцию
от двух переменных, значения которой сильно кореллированы. Такая избыточность
представления может быть использована. Прекрасным приложением является понятие
«скелетона» сигнала, извлеченное из непрерывного вейвлет-преобразования (НВП),
применяемое для нелинейной фильтрации.
3.1.2. Дискретное вейвлет-преобразование
К сожалению, концепция непрерывного вейвлет преобразования обладает своими
недостатками. Параметры a и b в формуле (3.1) меняются непрерывно, что приводит к
избыточному представлению спектра сигнала.
В некоторых задачах это, несомненно, является плюсом, кроме того, благодаря своей
избыточности спектры непрерывного преобразования достаточно наглядны. Однако
платой за эту избыточность является сравнительно невысокая скорость выполнения
преобразования, требующая вычисления интегралов для каждого из значений обоих
параметров a и b . Кроме того, поскольку на практике все сигналы, с которыми имеют
дело физики, имеют дискретную природу, то вопрос о целесообразности применения
масштаба вейвлета, покрывающего, к примеру, полторы точки исходного сигнала остается
открытым. Таким образом, более употребительными при компьютерных вычислениях с
реальными данными стали дискретные вейвлет-преобразования (ДВП).
Формула для дискретного вейвлет-преобразования получается из (3.1) в
предположении, что a , b принимают только дискретные значения: a a0m , b nb0 a0m , m ,
n пробегают значения из Z , величины a0 1 , b0 0 - фиксированные.
Wm,n ( f ) a0
m / 2
dtf (t ) a
m
0
t nb0
(3.4)
Разные значения m соответствуют разной ширине вейвлетов, поэтому узкие (высокие
частоты) вейвлеты сдвигаются малыми шагами, чтобы покрыть весь временной спектр, в
то время как более широкие (низкие частоты) вейвлеты сдвигаются большими шагами.
Соответствующие вейвлеты с дискретными индексами выглядят как
(3.5)
m,n (t ) a0m / 2 (a0mt nb0 ) .
В дискретном случае, вообще говоря, не существует формулы обращения,
аналогичной (3.2) для непрерывного случая. Восстановление f из W f , если оно вообще
возможно, должно, таким образом, производится другими методами.
Как и в непрерывном случае, ДВП часто дает весьма избыточное описание исходной
функции. Эта избыточность может быть использована (например, можно вычислить
вейвлет-преобразование лишь приблизительно, при этом восстановить f с достаточно
хорошей точностью) или ликвидирована путем удаления его несущественных значений.
Выбор вейвлета , используемого в НВП или в семействе вейвлетов с дискретными
индексами, существенно ограничен требованием, чтобы C , определенная по формуле
(3.3), была конечной. Из практических соображений обычно берется хорошо
сконцентрированной во временной и частотной областях, но это, тем не менее, оставляет
достаточно свободы для выбора. (В разделе, посвященном кратномасштабному анализу,
будет показано, как, отказываясь во многом от этой свободы, выбора, можно получить
ортонормированные базисы вейвлетов.)
3.1.3. Пороговое обрезание вейвлет-коэффициентов
Полезным свойством вейвлет-разложения является возможность проанализировать
структуру сигнала как в частотной области, так и во временной. В соответствии с этим
задача сглаживания приобретает дополнительные возможности. Во-первых, можно
производить обрезание по спектру частот, и, во-вторых, одновременно с этим, анализируя
величину вейвлет-коэффициентов, также влиять на сигнал, путем их изменения.
Существуют два основных общепринятых правила порогового обрезания вейвлеткоэффициентов:
0, w ,
1) «жесткое» (hard thresholding): w wt
w, w .
0, w ,
2) «мягкое» (soft thresholding): w wt
sign ( w)( w ), w .
Здесь - значение порога обрезания (threshold value), выбираемое обычно в процентах от
стандартного отклонения вейвлет-коэффициентов данного уровня.
Рис. 3.1. «Жесткое» (слева) и «мягкое» (справа) пороговое обрезание.
3.2. Кратномасштабный анализ
Дискретное вейвлет-преобразование строится с помощью кратномасштабного
анализа.
Понятие кратномасштабного анализа сформулировано осенью 1986 Малла (Mallat) и
Мейером (Meyer). Кратномасштабный анализ обеспечивает естественную основу для
понимания базисов вейвлетов и для построения новых примеров. История
формулирования понятия кратномасштабного анализа является прекрасным примером
того, как приложения стимулируют теоретические изыскания. Малла впервые услышал о
базисах Мейера, работая над анализом изображений, в котором идея изучения
изображений одновременно для разных масштабов и сравнения результатов была
популярна многие годы. Это подвигло его к рассмотрению ортонормированных базисов
вейвлетов как инструмента для математического описания «приращения информации»,
необходимого для перехода от грубого приближения к приближению более высокого
разрешения. Такое понимание выкристаллизировалось в концепцию кратномасштабного
анализа.
3.2.1. Основная идея
Кратномасштабный анализ состоит из последовательности пространств
аппроксимации V j . Более точно, замкнутые подпространства V j удовлетворяют
включениям
... V2 V1 V0 V1 V2 ... ,
(3.6)
где
(3.7)
V j L2 ( R) ,
jZ
V 0.
(3.8)
j
jZ
Если через Pj обозначить оператор ортогонального проектирования на V j , то (3.7)
гарантирует, что
lim P f f
j
j
для всех
f L2 ( R) . Существует много цепочек
пространств, удовлетворяющих (3.6) – (3.8), которые не имеют отношения к
«кратномасштабности». Кратномасштабность является следствием дополнительного
требования
(3.9)
f V j f (2 j ) V0 .
Все эти пространства являются масштабируемыми версиями центрального пространства
V0 . Другое свойство, которое требуется от кратномасштабного анализа: инвариантность
V0 по отношению к сдвигам на целые числа:
f V0 f ( n) V0 для всех n Z .
(3.10)
Вместе с (3.9) это влечет f ( 2 n) V j для всех n Z , если f V j . Наконец,
j
требуется, чтобы существовала V0 такая, что
0,n ; n Z является ортонормированным базисом в V0 ,
(3.11)
где для всех j, n Z , j ,n (t ) 2 j / 2 (2 j t n) . Вместе (3.11) и (3.9) приводят к тому, что
; n Z - ортонормированный базис в V j для всех j Z . В литературе часто
называется «масштабирующей функцией» кратномасштабного анализа.
j ,n
Основной принцип кратномасштабного анализа таков: для любого набора замкнутых
подпространств, удовлетворяющего (3.6) – (3.11), существует такой ортонормированный
базис вейвлетов j ,k ; j , k Z для L2 ( R) , где j ,k (t ) 2 j / 2 (2 j t k ) , что для всех f из
L2 ( R)
Pj 1 f Pj f f , j ,k j ,k .
(3.12)
kZ
( Pj - ортогональное проектирование на V j .) Более того, вейвлет можно
сконструировать в явном виде. Посмотрим, как это делается.
Для каждого j Z , определим W j как ортогональное дополнение V j в V j 1 . Имеем
и
V j 1 V j W j
(3.13)
W j W j , если j j .
(3.14)
(Если j j , например, то W j V j W j .) Следовательно, для j J
J j 1
V j VJ
W
k 0
J k
,
(3.15)
в котором все подпространства ортогональны. Ввиду (3.7) и (3.8) это влечет
L2 ( R) W j ,
(3.16)
jZ
что означает разложение L2 ( R) на взаимно ортогональные подпространства. Более
того, пространства W j наследуют от V j свойство масштабирования (3.9):
(3.17)
f W j f (2 j ) W0 .
Формула (3.12) эквивалентна высказыванию, что для фиксированного j семейство
j ,k ; k Z образует ортонормированный базис в W j . Имея (3.16), (3.7), (3.8), мы
автоматически получаем, что весь набор j ,k ; j , k Z является ортонормированным
базисом для L2 ( R) . С другой стороны, (3.17) гарантирует, что если 0,k ; k Z ортонормированный базис в W0 , то j ,k ; k Z будет ортонормированным базисом в W j
для любого j Z . Так, наша задача сводится к нахождению такой W0 , что функции
( k ) образуют ортонормированный базис в W0 .
3.2.2. Быстрые вычислительные алгоритмы
Кратномасштабный анализ естественным образом приводит к иерархической и
быстрой схеме вычисления вейвлет-коэффициентов данной функции. Допустим, что мы
уже вычислили (или имеем заданными) скалярные произведения f и j ,k для некоторого
заданного мелкого масштаба. Произведя масштабирование наших единиц измерения (или
масштабируя f ), мы можем предполагать, что номер этого уровня равен j 0 . Тогда
легко вычислить f , j ,k для j 1 . Прежде всего, имеем
hn 1,n ,
(3.18)
n
где hn , 1,n и
h
nZ
n
2
1.
Тогда, как показано в [3], можно выбрать W0 в виде
(3.19)
g n 1,n ,
n
где g n , 1,n (1) n hn1 . Следовательно,
j ,k (t ) 2 j / 2 (2 j t k ) 2 j / 2 g n 21/ 2 (2 j 1 t 2k n)
n
(3.20)
g n j 1, 2 k n (t ) g n2 k j 1,n (t ).
n
Отсюда
n
f , 1,k g n2 k f , 0,n , т.е. скалярные произведения
n
f ,
помощью свертки последовательностей
0 ,n
nZ
и
f , 1,k
g
n nZ
получены с
с последующим
сохранением лишь четных компонент. Аналогично, имеем соотношения
f , j ,k g n2 k f , j 1,n ,
(3.21)
n
f , j ,k , прибегнув к той же операции
которые можно использовать для вычисления
f , j 1,k . Но в силу (3.18) мы
(свертка с g , уменьшение вдвое числа членов), зная
получаем
j ,k ( x) 2 j / 2 (2 j x k ) hn2 k j 1,k ( x) ,
(3.22)
n
откуда
f , j ,k hn2 k f , j 1,k .
(3.23)
n
f , 0,n , вычисляем
Дальнейшая процедура становится ясной: начав с
формуле (3.21) и
f ,1,k
чтобы вычислить
f , 1,k
по
по формуле (3.23). Затем вновь можем применить (3.21) (3.23),
f , 2,k
f , 2,k ,
по
f ,1,n , и так далее… На каждом шаге мы
f , j ,k
вычисляем не только вейвлет-коэффициенты
на соответствующем j -м уровне,
но также и f , j ,k . для того же j -го уровня, что используется при вычислении вейвлеткоэффициентов на следующем уровне.
Весь процесс можно рассматривать, как вычисление последовательных
приближений f и разности между «информацией» на двух последовательных уровнях. С
этой точки зрения мы начинаем с самого мелкого масштабного приближения к f ,
f 0 P0 f (напомним, что Pj - ортогональный проектор на V j ; через Q j обозначим
ортогональный проектор на W j ) и разложим
f 0 V0 V1 W1 на
f 0 f 1 1 , где
f 1 P1 f 0 P1 f - следующее более грубое приближение f в кратномасштабном анализе,
а 1 f 0 f 1 Q1 f 0 Q1 f - «потери» при переходе f 0 f 1 . В каждом из пространств
V j , W j мы имеем ортонормированные базисы j ,k kZ , j ,k kZ , соответственно, так что
f 0 cn0 0,n ,
n
f 1 c1n1,n ,
1 d n1 1,n .
n
n
Формулы (3.21), (3.23) выражают воздействие преобразования 0,n nZ 1,n , 1,n nZ в
V0 на коэффициенты ортогонального базиса:
c1k hn 2 k cn0 ,
n
d k1 g n2 k cn0 .
(3.24)
n
Вводя обозначения a (an ) nZ , a (an ) nZ и ( Ab) k a2 k n bn , это можно переписать в
n
виде
c1 Hc 0 , d 1 Gc 0 .
Более грубое приближение
f 1 V1 V2 W2
f 1 f 2 2 , f 2 V2 , 2 W2 , где
f 2 cn2 2,n , 2 d n2 2,n .
n
снова
можно
разложить
в
n
Мы опять имеем
c 2 Hc1 , d 2 Gc1 .
Схематически это представлено на рис. 3.2.
Рис 3.2. Схема вейвлет-разложения.
На практике мы останавливаемся после конечного числа уровней. Это означает, что
мы переписали информацию f , 0,n nZ c 0 через d 1 , d 2 , d 3 ,..., d J и конечное грубое
приближение c J , т.е.
f ,
j ,k
kZ , j 1,..., J
и
f ,
J ,k
kZ
. Поскольку все сделанное является
последовательностью преобразований ортогональных
задается сопряженными матрицами. Точнее
f j 1 f j j ckj j ,k d kj j ,k ;
k
откуда
cnj 1 f
j 1
h
базисов, обратная операция
k
, j 1,n ckj j ,k , j 1,n d kj j ,k , j 1,n
k
c g n2 k d
j
n2 k k
j
k
k
(3.25)
k
(используем (3.20), (3.22)).
Итак, для дискретных сигналов концепция ДВП состоит в следующем: вместо
первоначального набора c k0 коэффициентов мы получаем совокупность наборов
c , d , которые и являются вейвлет-преобразованием сигнала, причем в отличии от
n
k
j
k
избыточного спектра НВП, количество полученных коэффициентов равно их количеству в
исходном массиве данных. Коэффициенты c kn
называются коэффициентами
аппроксимации, а d kj - деталями, соответствующими уровню разложения j .
3.2.3. Связь с субполосной фильтрацией
Фундаментальным, и до некоторой степени
удивительным выводом
кратномасштабного анализа является факт связи между вейвлетами и банком фильтров.
Уравнение (3.18) показывает эту связь и называется масштабирующим уравнением.
В цифровой обработке сигнала члены (3.24) и (3.25) являются шагами анализа и
синтеза в схеме субполосной фильтрации с точным восстановлением. В двухканальной
схеме субполосной фильтрации берется свертка входящей последовательности (cn0 ) nZ с
двумя фильтрами, низкочастотным и высокочастотным. Затем две полученные
последовательности прореживаются, т.е. удерживаются лишь четные (или нечетные)
компоненты. Именно это происходит в (3.24).
Выбор вейвлет-функций, по которым будет произведено разложение в результате
итерационной процедуры, зависит от применяемых фильтров. Критериями для выбора
фильтров и соответствующих им вейвлетов могут служить, например, желание получить
разложение по симметричным и ортогональным вейвлет-функциям. К сожалению,
доказано, что все, за исключением простейшего вейвлета Хаара, ортогональные наборы
вейвлетов несимметричны. На рис 3.3. изображена функция из семейства Добешивейвлетов с четырьмя нулевыми моментами.
Рис. 3.3. Функция из семейства Добеши-вейвлетов с четырьмя нулевыми моментами.
В целом, субполосная фильтрация используется, конечно, не просто для разложения
и восстановления. Целью игры является сжатие или обработка между этапами разложения
и восстановления. Во многих приложениях (анализ изображений, например) сжатие после
субполосной фильтрации более осуществимо, чем в отсутствии фильтрации.
Восстановление после применения таких схем сжатия (квантование) не идеально, однако
существует надежда, что с помощью специально сконструированных фильтров искажение
вследствие квантования можно сделать малым, при этом достигнув значительного
коэффициента сжатия.
4. Обработка смоделированных сигналов. На рис. 4.1., 4.2. изображены
смоделированные сигналы на интервале 250 мкс до и после наложения
двадцатипроцентного нормального шума и высокочастотной наводки, равной 25 кГц.
150
100
50
0
0
10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170 180 190 200 210 220 230 240 250
Рис. 4.1. Смоделированнный сигнал на интервале 250 мкс до наложения шума и наводок.
150
100
50
0
10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170 180 190 200 210 220 230 240 250
Рис. 4.2. Смоделированный сигнал на интервале 250 мкс с двадцатипроцентным нормальным
шумом и наведенной частотой 25 кГц.
На интервале 2 с на чистый сигнал (рис. 4.3) накладываются шум, распределенный
по нормальному закону, гармоники частоты 150 Гц и дискретные помехи. Полученный в
результате этого наложения сигнал изображен на рис. 4.4.
150
100
50
0
0
1
2
Рис. 4.3. Смоделированнный сигнал на интервале 2 с до наложения шума и
наводок.
150
100
50
0
0
1
2
Рис. 4.4. Смоделированный сигнал с двадцатипроцентными нормальным
шумом и наводкой 150 Гц и дискретными помехами (60 - 100%).
4.1. Обработка, основанная на преобразовании Фурье
Обычное преобразование Фурье функции f (t ) , определенной на интервале ;
производится по формуле
1 ~
f (t )
f ( )e it d ,
(4.1)
2
где
~
f ( )
f (t )e
it
содержит
dt
все
возможные
гармонические
составляющие
первоначальной функции и называется «преобразованием Фурье» или «Фурье-образом»
функции f (t ) .
Формула (4.1) имеет место лишь в случае абсолютной интегрируемости f (t ) , т.е.
если существует интеграл
f (t ) dt и f (t ) имеет «ограниченную вариацию» (т.е. не
может иметь бесконечного числа максимумов и минимумов) в каждом конечном
интервале [5].
Метод обработки дискретного сигнала, основанный на преобразовании Фурье
состоит в следующем. После Фурье-преобразования анализируемого сигнала в его спектре
приравниваются к нулю коэффициенты, соответствующие тем частотам(гармоникам), от
которых необходимо избавится в исходном сигнале.
150
100
50
0
10
20
30
40
50
60
70
80
90 100 110 120 130 140 150 160 170 180 190 200 210 220 230 240 250
Рис 4.5. Смоделированный сигнал на интервале 250 мкс после вырезания из его
Фурье-спектра частоты 25 кГц.
150
100
50
0
1
2
Рис 4.6. Смоделированный сигнал на интервале 2 с после вырезания из его Фурьеспектра гармоник частоты 150 Гц.
На рис. 4.5., 4.6. приведены результаты обработки смоделированных сигналов с
помощью описанного метода.
Видно, что в первом случае нормальный шум исчезает, но высокочастотная наводка
подавляется не полностью. Во втором случае не удается избавиться от сильных
дискретных помех, так как они не лежат в узком диапазоне частот.
4.2. Обработка с помощью Добеши-вейвлетов
Преобразование смоделированного сигнала, представляющего собой выборку
длиной N 2 k , k Z , происходит в три этапа:
а) Прямое вейвлет-преобразование с разложением до n -го уровня ( nmax k 2 ).
б) Отбрасывание на каждом j -м уровне вейвлет-коэффициентов W j ,i , для
которых выполняется условие: W j ,i T j ,где T j – порог обрезания j -го уровня,
определяемый сравнением вейвлет-коэффициентов исходного и зашумленного
сигналов на данном уровне.
в) Восстановление сигнала с помощью обратного вейвлет-преобразования.
На рис. 4.7. и 4.9. изображены сигналы, обработанные с помощью Добеши-вейвлетов
8-го порядка.
150
100
50
0
10
20
30
40
50
60
70
80
90 100 110 120 130 140 150 160 170 180 190 200 210 220 230 240 250
Рис. 4.7. Вид сигнала на интервале 250 мкс после обработки с помощью алгоритма,
использующего разложение по вейвлет-функциям.
С помощью вейвлетов достаточно легко устранить нормальный шум, просто
приравнивая к нулю вейвлет-коэффициенты на самых верхних уровнях вейвлет-спектра.
Кроме того, в отличие от предыдущего случая, оказывается значительно проще
уничтожить высокочастотную наводку, выбранную в модели равной 25 кГц (рис 4.7.).
Преимуществом описанного метода является также и то, что с его помощью удается
избавиться от пикообразных дискретных помех (рис 4.9.), так как они хорошо различимы
на частотно-временной структуре вейвлет-спектра обрабатываемого сигнала (рис 4.8.,
внизу).
Ограничением данного метода является соотношение помеха/полезный сигнал,
которое не должно превышать 85%.
Рис 4.8а Верхняя часть вейвлет-спектра (с выделенным 9-м слоем) смоделированного сигнала
16
14
12
10
8
6
4
2
0
-2
-4
-6
-8
0
200
400
600
800
1 000
1 200
1 400
1 600
1 800
2 000
Рис 4.8б. график вейвлет-коэффициентов 9-го слоя рис 4.8.а.
150
100
50
0
0
1
Рис. 4.9. Вид сигнала на интервале 2 с после обработки с помощью вейвлет-разложения
Литература
1. Н.М. Астафьева, УФН, 1996, т. 166, c. 1145.
2. I.Dremin et al, Wavelets and their use, на сайте
http://arxiv.org/PS_cache/hep-ph/pdf/0101/0101182.pdf
3. W.Sweldens, Building your own wavelets at home
считать с сайта http://citeseer.nj.nec.com/513562.html
Еще больше получишь, если в www.google.ru наберешь “вейвлет анализ”
2

