jjiii 1 2 1 − + + −•−−•−− −−⊗−−•−−⊗−K КОНКУРЕНЦИЯ В

Математическое моделирование и оптимальное управление
Вестник Нижегородского университета
им. Н.И. Лобачевского, 2007, № 2, с. 186–191
А.С. Мартынова
186
УДК 517.925.54
КОНКУРЕНЦИЯ В ПРОЦЕССАХ САМОСБОРКИ ЛИНЕЙНЫХ ЦЕПЕЙ
 2007 г.
А.С. Мартынова
Нижегородский госуниверситет им. Н.И. Лобачевского
martynova@vist.nnov.ru
Поступила в редакцию 19.02.2007
Обнаружено, что конкуренция в самосборке линейных цепей с элементами двух типов может
порождать неустойчивость состояния равновесия. Рассмотрены два способа конкуренции: через
интенсивности образования и через интенсивности разрыва связей. Гиперцикл конкуренции, напротив,
сохраняет устойчивость состояния равновесия. Полученные результаты отражают некоторые
особенности развивающихся систем различной природы.
Постановка задачи
Пусть имеются два типа элементов,
обозначим их как тип 1 и тип 2, и достаточно
много неразличимых копий каждого из них
равномерно заполняет некоторый замкнутый
объём. Независимо перемещаясь и сталкиваясь
между собой, копии элементов могут
взаимодействовать друг с другом, образуя
направленные связи. После образования связи
между элементами появляются компоненты или
линейные цепи из двух звеньев, составленные
из этих элементов. Эти цепи, в дальнейшем при
взаимодействии с другими элементами, могут
расти до сколь угодно длинных цепей. Будем
считать число копий всех элементов настолько
большим, что при взаимодействиях их друг с
другом они могут образовывать бесконечные
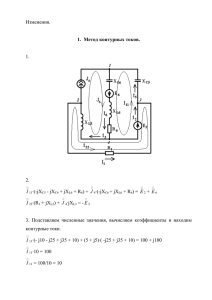
цепи. Цепи могут быть сколь угодно большими,
но никогда не могут превратиться в замкнутые
кольца, то есть зациклиться (рис. 1).
−⊗ −− • −− ⊗ −−K−− • −− • −
i
i +1
i+2
j −1
j
Рис. 1
Будем предполагать, что образовавшиеся
связи между элементами цепи не являются
«вечными» и при самосборке возможны
разрывы в цепях. Это предположение
недопустимо для биополимеров, таких как ДНК
и РНК, но является справедливым для
химических полимеров. Однако
если в
полученной для химических полимеров модели
принять параметры, описывающие разрывы в
цепях, равными нулю, то получившаяся модель
будет актуальна для описания и биополимеров.
Образования и разрывы связей между
элементами в цепях будем описывать с
помощью интенсивностей образования и
разрыва связей – p и q. Отметим, что
интенсивности образования и разрыва связей
являются аналогами скоростей реакций в
химических моделях.
Под конкуренцией в линейных цепях будем
понимать такой тип взаимодействий между
элементами самосборки, при котором:
– рост концентрации одного типа связи
препятствует появлению или сохранению
других типов связей;
и/или
– скорость появления одного типа связи
увеличивается при увеличении концентрации
этой связи в самосборке.
Последнее
условие
сродни
условию
автокатализа, которое заключается в том, что
константа скорости появления некоторого
вещества увеличивается при увеличении
концентрации этого вещества в химической
реакции [6].
Термин
«конкуренция»
введен
из-за
схожести
процесса
самосборки
с
рассмотренным выше типом взаимодействий –
с математическими моделями естественного
отбора
[1].
Два
различных
условия
существования конкуренции в самосборке дают
два различных способа ее моделирования –
через интенсивности разрыва
q и через
интенсивности образования связей p .
Отметим, что конкуренция является одним
из видов объемных взаимодействий процессов
самосборки, но отдельное ее исследование
позволяет
наглядно
интерпретировать
получаемые результаты [4].
Модель марковского процесса самосборки
линейных
цепей
была
предложена
и
Конкуренция в процессах самосборки линейных цепей
исследована М.Л Таем [3]. Им же было найдено
интегральное
многообразие.
Для
моделирования конкуренции в линейных цепях,
в рамках уже существующей математической
модели, достаточно лишь изменить вид
интенсивностей образования и разрывов связей.
Поэтому дальнейшее исследование динамики
этого процесса будем проводить на найденном
интегральном многообразии:
y&11 = ( D1 − y11 − y12 ) ×
× p11 ( D1 − y11 − y21 ) − q11 y11 ;
y&12 = ( D1 − y11 − y12 ) ×
× p12 ( D2 − y12 − y 22 ) − q12 y12 ;
y& 21 = ( D2 − y 21 − y 22 ) ×
(1)
× p21 ( D1 − y11 − y21 ) − q21 y21 ;
y& 22 = ( D2 − y21 − y22 ) ×
× p22 ( D2 − y12 − y 22 ) − q22 y22 .
Отметим, что конкуренция (можно назвать
ее материальной) за ресурсы (элементы
самосборки) уже присутствовала в процессе
самосборки линейных цепей. Действительно,
объем, в котором происходит процесс
самосборки, является замкнутым, а число копий
всех элементов пусть и достаточно большое, но
всё же ограничено. Однако материальная
конкуренция не приводит к смене устойчивости
состояния
равновесия
на
интегральном
многообразии [3] .
Конкуренция между
гомо- и гетеросвязями
Φ = {( y11 , y12 , y21 , y22 ) : 0 < y11 +
+ y12 ; y11 + y 21 < D1 , 0 < y12 +
+ y22 ; y21 + y 22 < D2 }
будет описываться с помощью следующей
динамической системы:
y&11 = ( D1 − y11 − y12 )( D1 − y11 − y21 ) ×
× p11 (1 + α11 y11 ) − q11 (1 + β12 y12 + β 21 y21 ) y11 ;
y&12 = ( D1 − y11 − y12 )(D2 − y12 − y22 ) ×
× p12 (1 + α12 y12 ) − q12 (1 + β11y11 + β22 y22 ) y12 ;
y&21 = ( D2 − y21 − y22 )(D1 − y11 − y21) ×
(3)
× p21(1 + α21y21) − q21(1 + β11y11 + β22 y22 ) y21 ;
y&22 = ( D2 − y21 − y22 )(D2 − y12 − y22 ) ×
× p22(1 + α22 y22 ) − q22 (1 + β12 y12 + β21 y21) y22 ,
где константы p11 , p12 , p21 , p22 , α11 , α12 ,
α 21 , α 22 > 0 , q11 , q12 , q21 , q22 , β11 , β12 ,
β 21 , β 22 > 0 . Подчеркиванием сверху здесь и
всюду ниже будем различать переменные, через
которые моделируем конкуренцию.
Справедлива следующая теорема.
Теорема 1. Если выполняются равенства
D1 = D2 = D , α11 = α12 = α 21 = α 22 = α ,
β11 = β12 = β 21 = β 22 = β ,
(2)
(4)
p11 = p12 = p22 = p21 = p ,
q11 = q12 = q22 = q21 = q ,
тогда у системы (3) в фазовом пространстве
(2) существует симметричное состояние
равновесия
Гомосвязью
будем
называть
связь,
образованную между двумя элементами одного
и того же типа, а связь между элементами
разных типов назовем гетеросвязью. Таким
образом, связь, образованная между элементами
в компоненте 11 или 22, будет гомосвязью, а
связь в компоненте 12 или 21 – гетеросвязью.
Подобная же терминология используется и в
химии: например, связи между одинаково и
разноименно заряженными ионами называют
гомо- и гетерополярными [6].
В случае конкуренции между гомо- и
гетеросвязями процесс самосборки линейных
цепей из двух элементов в фазовом
пространстве
187
( y , y , y , y ),
где
0< y<
D
,
2
которое будет устойчивым, если
αβ <
1
,
2 y2
(5)
и неустойчивым при нарушении условия (4).
Доказательство. 1) Для того чтобы
( y , y , y , y ) было состоянием равновесия,
нужно, чтобы оно удовлетворяло уравнению
( D − 2 y ) 2 p (1 + α y ) = q y (1 + 2 β y ) . (6)
При выполнении равенств (3) и при yij = y
все уравнения системы (2) примут вид:
y& ij = ( D − 2 y ) 2 p (1 + α y ) − q y (1 + 2 β y ) , (7)
что
и
доказывает
существование
симметричного состояния равновесия
у
системы (3).
2) Докажем теперь устойчивость состояния
равновесия ( y , y , y , y ).
А.С. Мартынова
188
Исследуем поведение интегральных кривых
системы (3) в окрестности состояния
равновесия: линеаризуем ее в окрестности
( y , y , y , y ) и составим характеристическое
уравнение. Оно будет иметь вид:
λ −a −b
−b
0
−b λ −a
0
−b
= 0,
−b
0
λ −a −b
0
−b
−b λ −a
(8)
где
( D − 2 y )( D + 2αy 2 )
<0,
y
( D − 2 y )(1 + αy )(1 + β D )
< 0.
b = −p
(1 + 2β y )
a = −p
Значения
a
и
b
получены
из
дифференцирования правых частей системы (3)
при подстановке значений производных в
состоянии равновесия ( y , y , y , y ), с учётом
равенств (4).
Упростим определитель в (6): вычтем
последний столбец из первого, а третий столбец
из второго. Затем к последней строчке
прибавим первую строчку, а к третьей строчке
вторую. Получим:
λ −a
0
−b
0
0
λ −a
0
−b
= 0.
0
0
λ − a − 2b
0
0
− 2b λ − a
Отсюда получаем
∆(λ ) = (λ − a )2 ((λ − a )2 − 4b2 ) =
= (λ − a )2 (λ − a − 2b)(λ − a + 2b) = 0 .
Видим, что три первых характеристических
корня будут строго отрицательными. Осталось
только проверить знак последнего корня.
λ4 = a − 2 b = −
будет устойчивым. Однако когда α и β будут
строго положительны и αβ >
1
2
> 2 , тогда
2
2y
D
λ 4 > 0 и состояние равновесия будет
неустойчивым.
Теорема 1 доказана.
Замечание 1: Условия (5) автоматически
выполнятся при α = 0
или
β = 0 , и,
следовательно, в случае, когда выполнено лишь
одно из условий конкуренции.
Замечание 2: Следует отметить, что
выполнение условия (5) зависит от величины
y в состоянии равновесия y . Это связано с
большим числом параметров в системе (3), и
этого можно избежать, если дополнить (3)
необходимыми значениями параметров. С
другой стороны, на y в условии (5) можно
смотреть как на новый параметр системы (3), и
он, к тому же, может быть найден численно на
ЭВМ.
Кроме этого, справедливо
Следствие. При выполнении равенств (3) в
2
области параметров αβ >> 2 (5) у системы
D
(3) существует неустойчивое симметричное
состояние
равновесия
( y , y , y , y ),
где
0< y<
D
.
2
Итак, аналитически обнаружили, что смена
устойчивости
симметричного
состояния
равновесия в процессе соперничества между
гомо- и гетерополимерными структурами при
«равных условиях борьбы» (4)
будет
происходить только при достаточно «сильной»
p(D − 2 y )
[( D + 2α y 2 ) ×
y (1 + 2 β y )
× (1 + 2 β y ) − 2 y (1 + αy )(1 + βD )] =
p( D − 2 y)
=−
× [( D − 2 y ) − 2 αβ y 2 ×
y (1 + 2 β y )
× ( D − 2 y )] = −
p ( D − 2 y )2
(1 − 2 αβ y 2 ) .
y (1 + 2 β y )
Видим, что в случае, когда (1 − 2 αβ y 2 ) > 0
или αβ <
1
, λ 4 < 0 , состояние равновесия
2 y2
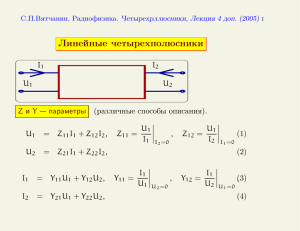
Рис. 2. Фазовый портрет системы (3), полученный
при следующих значениях параметров: D = 1, α = 6,
β = 4, p = 1, q = 1 . Крестиками отмечены два
устойчивых состояния равновесия, биссектрисой –
интегральное многообразие, на котором находится
неустойчивое симметричное состояние равновесия
Конкуренция в процессах самосборки линейных цепей
конкуренции,
выраженной
и
через
интенсивности образования
p, и через
интенсивности разрыва q. В ходе численного
эксперимента на ЭВМ (рис. 2) обнаружено, что
нарушение устойчивости повлечет за собой
появление в фазовом пространстве (2) еще двух
состояний равновесия. Они будут устойчивы, и
в одном из них преобладает концентрация
гомосвязей, а в другом – гетеросвязей. Процесс
самосборки линейных цепей в этом случае
будет приходить к одному или другому
«лидерству» в зависимости от выбора
начальных условий. Нечто подобное можно
увидеть в утверждении одной из гипотез о
превосходстве существующего, единого для
всей биосферы, генетического кода [5]. В этой
гипотезе принимается, что все варианты кода
были равноправны (условия (4)), но в
результате взаимодействия между разными
популяциями «случайно» (за счет выбора
начальных
условий)
был
выбран
существующий сейчас код. Также существует
другая точка зрения – гипотеза, утверждающая,
что запоминание единого кода произошло за
счет его превосходства над другими вариантами
кода [7]. Другими словами, выбор кода стал
результатом естественного отбора в эволюции.
К сожалению, ни одну из этих гипотез
невозможно проверить, т.к. для этого требуется
провести очень длительный по времени
эксперимент
(биологическая
эволюция
предположительно длилась около 109 лет).
Гиперцикл конкуренции
Теперь будем считать, что все концентрации
связей конкурируют между собой. Причем рост
концентрации связи 11 приводит к увеличению
интенсивности разрыва связи 12, а рост
концентрации связи 12 – к росту интенсивности
разрыва для связи 21. В свою очередь, рост
концентрации связи 21 приводит к росту
разрывов связей 22, рост концентрации которых
увеличивает интенсивность разрыва связей 11.
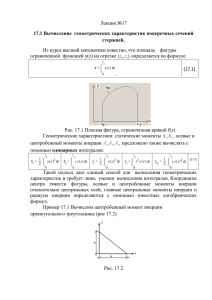
Схематично эти
взаимодействия
между
концентрациями связей можно изобразить так:
189
Из рисунка 3 видно, что теперь в самосборке
устанавливаются
конкурирующие
взаимодействия,
имеющие
замкнутую
(циклическую) структуру. Биофизик М. Эйген
назвал подобную систему взаимодействий
гиперциклом [7, 8]. Поэтому, по аналогии,
назовем
рассматриваемые в
самосборке
линейных цепей взаимодействия гиперциклом
конкуренции.
Следует
заметить,
что
гиперцикл
конкуренции имеет существенное отличие от
«классического» гиперцикла Эйгена – Шустера.
«Классический» гиперцикл возможен только
для
самогенерирующихся
динамических
систем,
когда
компоненты
гиперцикла
участвуют в синтезе друг друга. А гиперцикл
конкуренции заключается в обратном –
компоненты
взаимодействия участвуют в
разложении друг друга.
Перечислим
основные
преимущества
гиперцикла конкуренции перед описанной
выше конкуренцией:
― Гиперцикл поддерживает «оптимальную»
конкуренцию
между
компонентами
самосборки, когда «преимущество одних не
идет в ущерб другим», и позволяет всем
структурам развиваться одновременно.
― Гиперцикл объединяет все связи при
самосборке в единую кооперативную систему,
способную к слаженному развитию, когда
преимущества одной связи могут быть
использованы для развития остальных связей.
― Гиперцикл – это одна из разновидностей
принципа обратной связи, позволяющей
системе динамически «приспосабливаться» к
условиям окружающей среды.
В случае гиперцикла конкуренции процесс
самосборки линейных цепей в фазовом
пространстве
(1)
будет
описываться
следующей динамической системой:
y&11 = ( D1 − y11 − y12 ) p11 ( D1 − y11 − y21 ) −
− q11 y11 (1 + β 22 y22 );
y&12 = ( D1 − y11 − y12 ) p12 ( D2 − y12 − y22 ) −
− q12 y12 (1 + β11 y11 );
y& 21 = ( D2 − y21 − y22 ) p21 ( D1 − y11 − y21 ) −
(7)
− q 21 y21 (1 + β12 y12 );
y& 22 = ( D2 − y21 − y22 ) p22 ( D2 − y12 − y 22 ) −
Рис. 3
q 22 y22 (1 + β 21 y21 ),
где константы p11 , p12 , p21 , p22 , q11 , q12 ,
q21 , q22 ,
β11 ,
β 12 , β 22 строго
положительны.
А.С. Мартынова
190
λ−a
Справедлива следующая теорема.
Теорема 2. Если выполняются равенства
∆1 ( λ ) =
D1 = D2 = D ,
β11 = β12 = β 21 = β 22 = β ;
p11 = p12 = p21 = p22 = p ,
q11 = q12 = q 21 = q 22 = q,
(8)
тогда у системы (7) в фазовом пространстве (2)
существует
устойчивое
симметричное
состояние
равновесия
( y , y , y , y ),
где
D
.
2
Доказательство. 1) Для того чтобы
( y , y , y , y ) было состоянием равновесия,
нужно, чтобы оно удовлетворяло уравнению
0< y<
−b
−b−c λ −a
−b
1
0
1
1
−b
−c
λ−a
0
−b
−b−c 1
.
Определим знак первого характеристического
корня:
λ1 = a + 2b + с = −
p( D − 2 y )
[( D + 2 y ) ×
y (1 + β y )
× (1 + β y ) + y ( D − 2 y ) β ] = −
p( D − 2 y )
×
y (1 + β y )
× [( D + 2 y ) + β y ( D + 2 y + D − 2 y )] =
p( D − 2 y )
[( D + 2 y ) + 2 yβ D ] < 0.
y (1 + β y )
Получили, что λ1 < 0 .
( D − 2 y ) 2 p (1 + α y ) = q y (1 + β y ). (9)
Преобразуем ∆1 (λ ) : вычтем последнюю
При выполнении равенств (8) и при yij = y
все уравнения системы (7) примут вид
y& ij = ( D − 2 y ) 2 p (1 + α y ) − q y (1 + β y ), (10)
что
и
доказывает
существование
симметричного состояния равновесия
у
системы (7).
2) Докажем теперь устойчивость состояния
равновесия ( y , y , y , y ). Для этого исследуем
поведение интегральных кривых системы (7) в
окрестности состояния равновесия. Линеаризуем
ее в окрестности ( y , y , y , y ) и составим
характеристическое уравнение. Оно будет иметь
вид:
−b
λ −a
−b−c λ −a
∆ (λ ) =
−b
−c
0
−b
строчку из всех остальных строк:
λ −a
0
с
∆1 (λ ) = − b − c λ − a + b
b+c
. (12)
−b
b−c
λ −a+b+c
Преобразуем определитель в (7) следующим
образом: вычтем из третьей строчки первую, а
затем прибавим к первому столбцу последний.
В результате этих действий получим:
λ −a+c
0
c
∆1 (λ ) =
0
λ −a+b
b+c =
,
0
b−с
λ −a+b
−b
0
λ −a
−c
= (λ − a + c ) ⋅ ∆ 2 (λ ),
−b
где
= 0, (11)
−b
∆ 2 (λ ) = (λ2 + R1λ + R2 ) ,
−b−c λ −a
R1 = b − a ,
где
D (D − 2 y )
a = −p
< 0 , b = − p (D − 2 y) < 0 ,
y
( D − 2 y )2 β
< 0.
(1 + β y )
Значения a , b и с получены из
дифференцирования правых частей системы (4)
при подстановке значений производных в
состоянии равновесия ( y , y , y , y ), с учётом
равенств (8).
Упростим определитель в (11), прибавив все
его столбцы к последнему:
∆ ( λ ) = ( λ − a − 2b − c ) ∆ 1 ( λ ) = 0 ,
где
c = −p
−
R2 = a 2 − 2ab + c 2 = a ( a − 2b) + c 2 .
Теперь можем определить
характеристического корня:
λ2 = a − c = −
знак
второго
p( D − 2 y )
×
y (1 + β y )
× [ D(1 + β y ) − yβ ( D − 2 y )] =
p( D − 2 y )
=−
[D + 2β y 2 ] < 0.
y (1 + β y )
Получили, что и λ 2 < 0 .
Определим условия устойчивости полинома
– условие отрицательности его
характеристических корней, применив к нему
критерий Раусса – Гурвица. Для выполнения
∆ 2 (λ )
Конкуренция в процессах самосборки линейных цепей
191
критерия необходимо и достаточно, чтобы R1 >0
и R2 >0.
Определим их знаки:
R1 = b − a =
p ( D − 2 y )( D − y )
> 0,
y
R2 = a(a − 2b) + c 2 .
Определим знак выражения в круглых
скобках в R2 : a − 2b = −
p ( D − 2 y )2
<0 .
y
Получили, что все слагаемые в R2 будут
строго положительны.
Итак, при всех β > 0 : R1 >0, R2 >0. Это и
завершает
доказательство
устойчивости
симметричного
состояния
равновесия
( y , y , y , y ).
Теорема 2 доказана.
Замечание: Теорема 2 будет справедлива и
для системы
y&11 = ( D1 − y11 − y12 ) p11( D1 − y11 − y21 ) −
− q11 y11 (1 + β 22 y22 );
y&12 = ( D1 − y11 − y12 ) p12 ( D2 − y12 − y22 ) −
Рис. 4
Действительно, с помощью равенств (8)
система (13) примет вид (7), и, следовательно,
для нее справедливы все выводы, полученные в
ходе доказательства теоремы 2.
Численный эксперимент на ЭВМ при
несимметричных параметрах взаимодействий
показал, что при D1 = D2 траектории системы
(7) приходят в
устойчивое состояние
равновесия ( y11 , y12 , y21 , y22 ). И в этом
состоянии будет преобладать та концентрация
связи, у которой соотношение интенсивностей
q
является наименьшим.
p
Таким образом, получили, что гиперцикл не
− q12 y12 (1 + β11 y11 );
нарушает устойчивости состояния равновесия
(13) соответствующей динамической системы и
y& 21 = ( D2 − y21 − y22 ) p21 ( D1 − y11 − y21 ) −
− q21 y21 (1 + β12 y12 );
y& 22 = ( D2 − y21 − y22 ) p22 ( D2 − y12 − y22 ) −
− q22 y22 (1 + β 21 y21 ),
поддерживает «оптимальную» конкуренцию
между
концентрациями
связей,
когда
преимущество одних концентраций связей не
приводит к уменьшению других концентраций.
когда гиперцикл конкуренции будет направлен
в другую сторону (рис. 4).
Список литературы
1. Вольтерра В. Математическая теория борьбы
за существование. – М.: Наука, 1976.
2. Леонтович А.М. Одна задача о самосборке
отрезков // Проблема передачи информации. 1975.
№ 15. С. 97–106.
3. Тай М.Л. Исследование стохастической
модели самосборки линейных цепей // Проблема
передачи информации. 1979. Т. 15. № 4. С. 40–52.
COMPETITION IN THE PROCESSES OF SELF-ASSEMBLY OF LINEAR CHAINS
A.S. Martynova
It is found that competition in self-assembly of linear chains with two types of elements can generate instability
of equilibrium. Two ways of competition are considered: via intensities of formation and via intensities of breakup
of relationships. On the contrary, the hypercycle of competition preserves the stability of equilibrium. The results of
this research reflect some features of developing systems of different nature.
192
А.С. Мартынова
4. Тай М.Л. Процессы самосборки с объемными
взаимодействиями // Докл. АН СССР. 1990. Т. 314.
№ 1. С. 189–193.
5. Романовский
Ю.М.,
Степанова
Н.В.,
Чернавский Д.С. Математическая биофизика. – М.:
Наука, 1984.
6. Эмануэль Н.М., Кнорре Д.Г. Курс химической
кинетики. – М.: Высшая школа, 1984.
7. Эйген М. Самоорганизация материи и
эволюция биологических макромолекул. – М.: Мир,
1982.
8. Эйген М., Шустер П. Гиперцикл. Принципы
самоорганизации макромолекул. – М.: Мир, 1982.