Гусев Н.С., Чернышев В.Л. Производная Ли, теорема
advertisement

М Г
Н. Э. Б
Н. С. Гусев, В. Л. Чернышев
П Л,
Ф,
Учебное пособие по дисциплине
«Управление движением»
Электронное учебное издание
© Московский Государственный технический университет
имени Н. Э. Баумана, 2011
Москва, 2011
УДК 514.7
Рецензенты:
Иванов Александр Олегович, д.ф.-м.н., механико-математический факультет
МГУ имени М. В. Ломоносова, профессор кафедры дифференциальной геометрии
и приложений;
Хорькова Нина Григорьевна, к.ф.-м.н., факультет фундаментальных наук
МГТУ имени Н. Э. Баумана, доцент кафедры прикладной математики (ФН-2)
Авторы: Гусев Никита Сергеевич, Чернышев Всеволод Леонидович
Производная Ли, теорема Фробениуса, дифференциальные формы / Н. С. Гусев,
В. Л. Чернышев.— М. : МГТУ имени Н. Э. Баумана, 2011.— 65 с.
В данном учебном пособии по дифференциальной геометрии и тензорному анализу даны
определения и приведен ряд основных свойств производной Ли векторных полей и гладких
дифференциальных форм. Доказаны инфинитезимальная формула Стокса и теорема Фробениуса.
По каждой из этих тем разобраны примеры и даны задачи для самостоятельной работы.
Предназначается студентам МГТУ имени Н. Э. Баумана, изучающим курс дифференциальной
геометрии и тензорного анализа, нелинейные динамические системы с управлением, а также
широкому кругу читателей.
Рекомендуется НМС МГТУ имени Н. Э. Баумана в качестве учебного пособия
© Гусев Н. С., Чернышев В. Л., 2011
Содержание
Предисловие
4
1 Предварительные сведения и обозначения
1 § Тензорные операции . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2 § Многообразия . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3 § Тензоры на многообразиях . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4 § Дифференциалы отображений и переносы ими тензоров . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5 § Поток векторного поля . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6 § Дифференцирование дифференциальных форм . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6
6
8
9
12
14
17
2 Построение производной Ли
7 § Переносы векторным полем и построение производной Ли . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
8 § Координатное представление . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9 § Бескоординатные свойства . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
10 § Инфинитезимальная формула Стокса . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
22
22
24
26
30
3 Теорема Фробениуса
11 § Леммы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
12 § Распределения и теорема Фробениуса . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
13 § Инволютивность распределения и дифференциальные формы . . . . . . . . . . . . . . . . . . . . . . . . . . . .
33
33
36
40
4
Разбор примеров
4.1 Дифференциальные формы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
14 § Вычисление значений . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
15 § Внешнее умножение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
16 § Дифференцирование . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.2 Производная Ли . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
17 § Вычисление производной Ли . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
18 § Инфинитезимальная формула Стокса . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.3 Теорема Фробениуса . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
19 § Одномерное распределение в трехмерном пространстве . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
20 § Двумерное распределение в трехмерном пространстве . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
43
43
43
45
47
48
48
51
53
53
54
5
Задачи для самостоятельного решения
5.1 Дифференциальные формы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
21 § Вычисление значений . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
22 § Внешнее умножение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
23 § Дифференцирование . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.2 Производная Ли . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
24 § Вычисление производной Ли . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
25 § Инфинитезимальная формула Стокса . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.3 Теория Фробениуса . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
26 § Одномерное распределение в трехмерном пространстве . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
27 § Двумерное распределение в трехмерном пространстве . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
57
57
57
58
58
59
59
59
60
60
60
Список обозначений
Предметный указатель
Список литературы
61
63
64
П
Данное учебное пособие охватывает элементарные понятия теории дифференциальных форм; в нем дается определение и алгебраические свойства производной
Ли, ее связь с дифференцированием форм и внутренним дифференцированием (инфинитезимальная формула Стокса); а также определяется понятие векторного распределения и обсуждается теорема Фробениуса о критерии вполне
интегрируемости в двух видах: с позиции инволютивности локального базиса распределения и с позиции свойств сопряженного с распределением набора
дифференциальных форм.
Пособие адресовано студентам МГТУ имени Н. Э. Баумана, углубленно изучающим курс дифференциальной геометрии и тензорного анализа, а также студентам и аспирантам, приступающим к изучению дифференциально-геометрического метода в задачах управления. Этот подход широко применяется в учебных
курсах (см., например, программу курса «Управление движением») и научных
исследованиях на кафедре «Математического моделирования» под руководством
ее заведующего профессора А. П. Крищенко (см., например, книгу [1]).
Углубленное изучение теории дифференциальных форм способствует повышению общематематической культуры будущих инженеров и специалистов по
прикладной математике и развитию у них современного взгляда на задачи механики и физики (см., например, известный учебник [2]). Для более глубокого
изучения вопросов, связанных с теоремой Фробениуса и инфинитезимальной
формулой Стокса, студентам и аспирантам кафедры рекомендуется к прочтению
англоязычная монография [3]. Студентам, знакомящимся с дифференциальногеометрическим подходом к задачам управления, рекомендуем обратить внимание на последние главы в книге [4].
Настоящее учебное пособие дополняет имеющиеся учебные материалы по
этой тематике, причем особое внимание уделено разбору примеров.
Предполагается, что читатель знаком с аналитической геометрией, алгеброй,
математическим анализом, теорией обыкновенных дифференциальных уравнений. Доказательства базовых свойств соответствующих объектов и операций не
приводятся. Читатель легко может найти их в указанных в списке литературы
учебниках, монографиях и методических пособиях: [5], [6], [7], [8], [9], [10], [11],
[12], [13]. При этом основные утверждения и теоремы доказаны полностью и с
высоким уровнем строгости.
Снабженное предметным указателем и списком используемых обозначений
пособие состоит из пяти частей. В первой вводятся понятия гладкого многообразия, тензорного поля на нем, кососимметрического тензорного поля, дифференциала отображения, потока векторного поля, скобки Пуассона. Доказывается
формула Картана. Во второй части вводится понятие переноса векторным полем и определяется производная Ли. Доказывается инфинитезимальная формула
Стокса. В третьей части обсуждаются распределения и доказывается теорема
Фробениуса.
Четвертая и пятая части могут рассматриваться отдельно от остальных, как
небольшой задачник с подробными решениями по дифференциальным формам,
производной Ли, применению теоремы Фробениуса. Отметим, что в этом данное
пособие дополняет известный сборник задач по дифференциальной геометрии
[14]. Приведенный в пятом разделе список задач для самостоятельного решения
может быть использован для контроля усвоения материала.
Данное учебное пособие подготовлено при частичной финансовой поддержке
грантов РНП 2.1.1/227 и МК-943.2010.1.
6
Предварительные сведения и обозначения
1. Предварительные сведения и обозначения
§1
Т
В
этом разделе предполагается, что задано линейное вещественное пространство V .
Определение. Для целого числа γ > 0 инъективное отображение τ из множества {1, . . . , γ} в него же называется перестановкой на множестве {1, . . . , γ} .
Определение. Пусть τ — перестановка на множестве {1, . . . , γ} ; тогда ее знаком
называется число sign τ ∶= (−1)ω , где ω — количество инверсий в перестанов⎫ ⎧ ⎫
ке τ , то есть пар ⟨α, β⟩ таких, что 1 ⩽ α < β ⩽ γ и τ⎧
⎩α⎭ > τ⎩β⎭.
Определение. Пусть p — ковариантный тензор на V валентности γ (то есть
γ -линейное отображение из V × . . . × V в R ), а τ — перестановка на множестγ раз
ве {1, . . . , γ} ; тогда обозначим действие перестановки на тензор:
⎫,
⎫ ∶= p⎧
(τ ↪ p)⎧
⎪
⎪
⎭
⎩ v1 , . . . , vγ ⎪
⎭
⎩vτ⎧⎩1⎫⎭, . . . , vτ⎧⎩γ⎫⎭⎪
где v1 , . . . , vγ ∈ V .
Определение. Ковариантный тензор p валентности γ на V кососимметричен
(или антисимметричен), если
τ ↪ p = (sign τ) ⋅ p
для всякой перестановки τ на множестве {1, . . . , γ} .
Определение. Пусть p — ковариантный тензор на V валентности γ ; тогда обозначим альтернацию тензора p :
alt p ∶=
1
γ!
⋅ ∑(sign τ) ⋅ (τ ↪ p),
τ
где сумма распространяется на все перестановки τ на множестве {1, . . . , γ} .
Утверждение. Пусть p — ковариантный тензор на V ; тогда тензор alt p кососимметричен. Если же сам тензор p кососимметричен, то alt p = p ; поэтому alt alt p = alt p для всякого ковариантного тензора p на V .
Определение. Пусть p1 , p2 — ковариантные тензоры на V валентности γ1 и
γ2 ; тогда их тензорное произведение есть ковариантный тензор p1 ⊗ p2 на V
валентности γ1 + γ2 , действующий на векторах v1 , . . . , vγ1 +γ2 ∈ V по формуле
⎫.
⎫ ⋅ p2 ⎧
⎫ = p1 ⎧
(p1 ⊗ p2 )⎧
⎪
⎪
⎭
⎭ ⎪
⎩vγ1 +1 , . . . , vγ1 +γ2 ⎪
⎭
⎩v1 , . . . , vγ1 ⎪
⎩v1 , . . . , vγ1 +γ2 ⎪
Н. С. Г, В. Л. Ч
7
Предварительные сведения и обозначения
Определение. Пусть p1 , p2 — ковариантные тензоры на V валентности γ1 и γ2 ;
1
2⎫
тогда обозначим их внешнее произведение: p1 ∧ p2 ∶= alt⎧
⎩p ⊗ p ⎭.
Утверждение. Операция ∧ ассоциативна и линейна по обоим аргументам.
Определение. Пусть на пространстве V задан ковариантный тензор p валентности γ > 0 ; тогда при произвольных векторах v1 , . . . , vγ ∈ V обозначим
α
ковариантный тензор p ←
Ð vα на V валентности (γ − 1) по формуле
без v
α
α
⎧v , . . . , v ⎫
v
,
.
.
.
,
vγ ⎫
(p ←
Ð vα )⎧
γ⎪
⎭ ∶= p⎪
⎩ 1
⎩ 1
⎭;
а если 1 ⩽ α1 < . . . < αβ ⩽ γ , то это определение индуктивно продолжим:
α1 ,...,αβ
αβ −β+1
α1 ,...,αβ−1
(p ←ÐÐÐÐ v1 , . . . , vβ ) ∶= (p ←ÐÐÐÐÐ v1 , . . . , vβ−1 ) ←ÐÐÐÐ vβ .
Пример. В пояснение последнего определения положим β = 3 и поэтапно вычислим:
α1 ,...,αβ
α1 ,α2 ,α3
(p ←ÐÐÐÐ v1 , . . . , vβ ) = (p ←ÐÐÐÐ v1 , v2 , v3 ) =
α3 −3+1
α1 ,α2
α1
α2 −2+1
α3 −3+1
= ((p ←ÐÐ v1 , v2 ) ←ÐÐÐ v3 ) = (((p ←Ð v1 ) ←ÐÐÐ v2 ) ←ÐÐÐ v3 );
если, например, γ = 6 , α1 = 2 , α2 = 4 , α3 = 6 , то последовательно («изнутри
наружу») будет
2
⎫
(p ←
Ð v1 ) = p⎧
⎩⋅, v1 , ⋅, ⋅, ⋅, ⋅⎭,
2
здесь (p ←
Ð v1 ) уже пятивалентен,
и его третий аргумент соответствует четвертому в p;
α2 −2+1
2
2
4−2+1
⎫
((p ←
Ð v1 ) ←ÐÐÐ v2 ) = ((p ←
Ð v1 ) ←ÐÐÐ v2 ) = p⎧
⎩⋅, v1 , ⋅, v2 , ⋅, ⋅⎭,
здесь валентность стала четыре,
и четвертый аргумент соответствует шестому в p;
α1
α2 −2+1
α3 −3+1
2
4−2+1
6−3+1
Ð v1 ) ←ÐÐÐ v2 ) ←ÐÐÐ v3 ) =
(((p ←Ð v1 ) ←ÐÐÐ v2 ) ←ÐÐÐ v3 ) = (((p ←
⎫
= p⎧
⎩⋅, v1 , ⋅, v2 , ⋅, v3 ⎭.
Определение. Пусть на пространстве V задан ковариантный тензор p валентности γ ⩾ 0 , и v1 , . . . , vβ ∈ V ; тогда обозначим внутреннюю производную
(v1 ⊗ . . . ⊗vβ )⌟p контравариантным тензором v1 ⊗ . . . ⊗vβ тензора p по формуле
⎧
1,...,β
γ!
⎪
⎪
⎪ (γ−β)! ⋅ (p ←ÐÐÐ vβ , . . . , v1 ), если β ⩽ γ
(v1 ⊗ . . . ⊗ vβ ) ⌟ p ∶= ⎨
⎪
⎪ 0,
⎪
если β > γ;
⎩
П Л, Ф,
8
Предварительные сведения и обозначения
а на все контравариантные тензоры распространим по линейности (то есть если контравариантный тензор есть конечная сумма указанных тензорных произведений, то производная им есть сумма производных его слагаемыми). Здесь
(v1 ⊗ . . . ⊗ vβ ) ⌟ p — ковариантный тензор на V валентности max{0, γ − β} .
Утверждение. Пусть p — ковариантный тензор на V , и v1 , v2 — контравариантные тензоры на V ; тогда
v1 ⌟(v2 ⌟ p) = (v1 ⊗ v2 ) ⌟ p .
Утверждение. Пусть p — кососимметричный ковариантный тензор на V , и v
— контравариантный тензор на V ; тогда
v ⌟ p = (alt v) ⌟ p .
Утверждение. Пусть p1 , p2 — кососимметричные ковариантные тензоры на V ,
причем p1 имеет валентность γ , и v ∈ V ; тогда
v ⌟(p1 ∧ p2 ) = (v ⌟ p1 ) ∧ p2 +(−1)γ+1 ⋅ p1 ∧(v ⌟ p2 ).
Везде далее применяется тензорное правило Эйнштейна:
если в некоторой формуле есть произведение величин с верхними и нижними
индексами, и какой-то переменный индекс встречается в этом произведении только
однажды как верхний и как нижний, то в формуле по этому индексу производится
суммирование слагаемых вида этого произведения, причем диапазон изменения
этого индекса в сумме определяется контекстом формулы.
§2
М
Определение. Пусть задано некоторое множество M ; скажем тогда, что
инъективное отображение c ∶ Rμ Ð→ M — карта размерности μ на множестве M . При этом для точки x из образа отображения c вещественные числа
x 1 , . . . , x μ называются ее локальными координатами (относительно карты c ),
μ⎫
1
если только x = c⎧
⎩x , . . . , x ⎭.
>
>
>
>
Определение. Пусть заданы две карты c1 , c2 одной размерности μ на одном множестве; тогда
• они непрерывно согласованы, если только отображение c1 −1 ○ c2 непрерывно, и его образ открыт (здесь c1 −1 обозначает обратное к c1 отображение);
Н. С. Г, В. Л. Ч
9
Предварительные сведения и обозначения
• они гладко согласованы, если только отображение c1 −1 ○ c2 бесконечно
дифференцируемо, и его образ открыт.
Определение. Пусть на множестве M задано конечное множество A карт одной размерности μ ; тогда скажем, что это множество A — атлас (или гладкий
атлас) размерности μ , если
• объединение образов всех карт из множества A есть множество M ;
• для всяких двух разных точек x1 и x2 множества M найдутся два непересекающиеся подмножества U1 и U2 множества M и две карты c1 и
c2 из A такие, что x1 ∈ U1 ⊂ im c1 , x2 ∈ U2 ⊂ im c2 , прообразы множеств
U1 и U2 соответственно картами c1 и c2 открыты;
• всякие две карты из множества A непрерывно согласованы (или гладко
согласованы).
Определение. Множество M с атласом размерности μ (или гладким атласом
размерности μ ) на нем называется многообразием (или гладким многообразием)
размерности μ .
Определение. Пусть задано гладкое многообразие M размерности μ ; тогда
• отображение f ∶ M Ð→ R называется гладким (кратко обозначим f ∈
∈ C∞ (M) ), если для всякой карты c заданного атласа бесконечно дифференцируема функция f ○ c ∶ Rμ Ð→ R ;
• если даны разные числа a, b ∈ R , то отображение k ∶ (a, b) Ð→ M называется гладким (оно задает гладкую кривую на многообразии M ), если
для всякой карты c заданного атласа бесконечно дифференцируема функция c−1 ○ k ;
• если же также задано гладкое мноообразие N , то отображение m ∶ M Ð→
Ð→ N называется гладким (кратко обозначим m ∈ C∞ (M, N) ), если для
всякой карты c1 атласа на многообразии M и карты c2 атласа на многообразии N бесконечно дифференцируема функция c2 −1 ○ f ○ c1 .
§3
Т
В этом разделе предполагается, что задано гладкое многообразие M
ности μ . Также здесь и в дальнейшем применяется обозначение ∂α
ной по аргументу с номером α .
П Л, Ф,
размерпроизвод-
10
Предварительные сведения и обозначения
Определение 1. Пусть x ∈ M ; тогда отображение v ∶ C∞ (M) Ð→ R называется касательным вектором в точке x ко многообразию M , если только
• для всяких a, b ∈ R и f, g ∈ C∞ (M) выполнено равенство
⎫
⎧⎫
⎧ ⎫
v⎧
⎩a ⋅ f +b ⋅ g⎭ = a ⋅ v⎩f⎭ + b ⋅ v⎩g⎭;
⎫ ⎧⎫ ⎧ ⎫ ⎧ ⎫ ⎧ ⎫
• если f, g ∈ C∞ (M) , то v⎧
⎩f ⋅ g⎭ = v⎩f⎭ ⋅ g⎩x⎭ + f⎩x⎭ ⋅ v⎩g⎭;
касательное пространство Tx M в точке x ко многообразию M — совокупность всех касательных векторов в точке x ко многообразию M .
Определение. Удобно обозначить T M ∶= ⋃ Tx M ; а для каждого вектора v из
x∈M
T M обозначим его проекцию tpr v ∶= x в «точку его приложения», где точка x —
единственная точка многообразия M такая, что v ∈ Tx M .
Замечание. Из Определения 1 очевидно, что Tx M — линейное вещественное
пространство.
Определение. Для гладкой кривой k ∶ (a − b, a + b) Ð→ M , где a ∈ R и b > 0 ,
⎫
вводится ее производная ∂1 k⎧
⎩a⎭ = v в точке (числе) a как касательный вектор
⎫
в точке k⎧
⎩a⎭ по формуле
⎫
⎧ ⎫ d
⎧⎫
v⎧
⎩f⎭ ∶= ∂1 (f ○ k)⎩a⎭ = dt ∣ (f ○ k)⎩t⎭,
t=a
f ∈ C∞ (M);
этот вектор называется касательным к этой кривой в точке (числе) a .
Определение. Если на многообразии M задана карта c , то обозначим частную
производную по координате с номерами α = 1, . . . , μ :
μ⎫
⎫
⎧ ⎫
⎧ 1
∂ α ∣x ⎧
⎩f⎭ ∶= (∂ α f)⎩x⎭ ∶= (∂α (f ○ c))⎩x , . . . , x ⎭,
>
>
>
>
f ∈ C∞ (M).
Замечание. Ясно, что ∂ α ∣x ∈ Tx M .
>
Утверждение. Векторы ∂ 1 ∣x , . . . , ∂ μ ∣x образуют базис (называемый каноническим) в линейном пространстве Tx M ; причем координаты вектора v ∈ Tx M
обозначаем v 1 , . . . , v μ :
v = v α ⋅ ∂ α ∣x .
>
>
>
>
>
>
Определение. Отображение u ∶ D Ð→ T M , где D — открытое подмножество многообразия M , называется векторным полем на множестве D , если
только
⎧ ⎫⎫
• для всякой точки x множества D верно tpr⎧
⎩u⎩x⎭⎭ = x ;
Н. С. Г, В. Л. Ч
11
Предварительные сведения и обозначения
• для произвольной карты с образом (обозначим его U ) во множестве
α⎧ ⎫
⎫α
D отображение u⎧
⎩x⎭ =∶ u ⎩x⎭ — гладкая функция от x ∈ U при
α = 1, . . . , μ .
>
>
Определение. Если u — векторное поле на множестве D , а f — гладкая
D
⎫
⎧ ⎫⎧ ⎫
функция, то для x ∈ D обозначим (u ▹ f)⎧
⎩x⎭ ∶= u⎩x⎭⎩f⎭,— дифференцирование
функции векторным полем.
⎫
Определение. Обозначим ∂ α ⎧
⎩x⎭ ∶= ∂ α ∣x ,— координатное векторное поле при
α = 1, . . . , μ и точке x из образа координатной карты.
>
>
Пример. Вычислим, например, производную векторным полем u с координат⎫
⎧ ⎫
ным выражением ∂ 1 ⎧
⎩x⎭ − ∂ 2 ⎩x⎭ функции f с координатным выражением
1
2
⎫
f⎧
⎩ x⎭ = x − x :
>
>
>
>
D
⎫
⎧ ⎫⎧ ⎫
(u ▹ f)⎧
⎩x⎭ ∶= u⎩x⎭⎩f⎭ =
2⎫
2⎫
⎧ 1
⎫
⎧ ⎫⎧ 1
= (∂ 1 ⎧
⎩x⎭ − ∂ 2 ⎩x⎭)⎩x − x ⎭ = ( ∂ 1 ∣x − ∂ 2 ∣x )⎩x − x ⎭ =
2⎫
1
2⎫
⎧ 1
= ∂ 1 ∣x ⎧
⎩x − x ⎭ − ∂ 2 ∣x ⎩x − x ⎭ =
1⎫
⎧ 2⎫
⎧ 1⎫
⎧ 2⎫
= ∂ 1 ∣x ⎧
⎩x ⎭ − ∂ 1 ∣x ⎩x ⎭ − ∂ 2 ∣x ⎩x ⎭ + ∂ 2 ∣x ⎩x ⎭ =
= 1 − 0 − 0 + 1 = 2.
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
Утверждение. Пусть на подмножестве D многообразия M заданы векторные
поля u1 и u2 ; тогда отображение, сопоставляющее гладкой функции f гладкую
D
D
D
D
функцию u1 ▹(u2 ▹ f) − u2 ▹(u1 ▹ f) является векторным полем на множестве D ;
D
D
D
D
D
оно обозначается ⟦u1 , u2 ⟧ (то есть ⟦u1 , u2 ⟧ ▹ f ∶= u1 ▹(u2 ▹ f) − u2 ▹(u1 ▹ f) ) и
называется коммутатором векторных полей (также называется скобка Пуассона
или скобка Ли); в локальных координатах коммутатор вычисляется по формуле
⟦u1 , u2 ⟧
α
>
β
>
β
>
= u1 ⋅ ∂ β u2α − u2 ⋅ ∂ β u1α .
>
>
>
>
Определение. Пусть x ∈ M ; тогда ковариантный тензор над Tx M валентности γ называется ковариантным тензором валентности γ в точке x ; множество
γ
всех таких тензоров обозначается T∗ x M ; при γ = 1 такие тензоры называются кокасательными векторами в точке x ; совокупность всех кокасательных
векторов в точке x обозначается T∗ x M .
γ
Определение. Удобно обозначить T∗ γ M ∶= ⋃ T∗ x M и T∗ M ∶= ⋃ T∗ x M ; и
x∈M
x∈M
обозначим проекцию тензора p из T∗ γ M в «точку его приложения»: tpr p ∶= x ,
γ
где точка x — единственная точка многообразия M такая, что p ∈ T∗ x M .
П Л, Ф,
12
Предварительные сведения и обозначения
Определение. Пусть x ∈ M и задана карта на многообразии M , в образе
которой лежит точка x ; тогда, поскольку координатные функции на пространстве Tx M суть одновалентные ковариантные тензоры в точке x , α -тую из них
обозначим d α ∣x по формуле
>
α
⎫
d α ∣x ⎧
⎩v⎭ ∶= v ,
>
>
где v ∈ Tx M и α = 1, . . . , μ .
Замечание. Легко видеть, что d 1 ∣x , . . . , d μ ∣x образуют базис линейного пространства T∗ x M , двойственный к базису ∂ 1 ∣x , . . . , ∂ μ ∣x пространства Tx M .
>
>
>
>
Утверждение. Всякий ковариантный тензор p валентности γ в точке x
многообразия M имеет однозначное координатное представление в базисе
d 1 ∣x , . . . , d μ ∣x :
>
>
p=p
α1 ,...,αγ ⋅
>
d
α1
>
∣x ⊗ . . . ⊗ d
αγ
>
∣x .
Определение. Отображение q ∶ D Ð→ T∗ γ M , где D — открытое подмножество многообразия M , называется ковариантным тензорным полем валентности γ на множестве D , если только
⎧ ⎫⎫
• для всякой точки x множества D верно tpr⎧
⎩q⎩x⎭⎭ = x ;
• для произвольной карты с образом (обозначим его U ) во множестве D
⎫
⎧ ⎫
при x ∈ U и α1 , . . . , αγ = 1, . . . , μ функция q⎧
⎩x⎭ α1 ,...,αγ =∶ q α1 ,...,αγ ⎩x⎭
гладкая.
>
>
α
⎫
Определение. Обозначим d α ⎧
⎩x⎭ ∶= d ∣x ,— координатное ковекторное поле при
α = 1, . . . , μ и точке x из образа координатной карты.
>
>
Определение. Пусть q — ковариантное тензорное поле валентности γ на
некотором подмножестве многообразия M , и u1 , …, uγ — векторные поля
на том же множестве; тогда обозначим
⎫
⎧ ⎫⎧u1 ⎧x⎫, . . . , uγ ⎧x⎫⎫
(q ◂ u1 , . . . , uγ )⎧
⎩ ⎭⎪
⎩x⎭ ∶= q⎩x⎭⎪
⎭,
⎩ ⎩ ⎭
где точка x из того же множества.
§4
Д
В этом разделе предполагается, что задано гладкое многообразие M
ности μ .
Н. С. Г, В. Л. Ч
размер-
13
Предварительные сведения и обозначения
Определение. Пусть f ∈ C∞ (M) и x ∈ M ; тогда обозначим дифференциал
функции f в точке x по формуле
⎫⎧ ⎫ ⎧ ⎫
df⎧
⎩x⎭⎩v⎭ ∶= v⎩f⎭,
где v ∈ Tx M и x ∈ M ,—
отображение, действующее на множестве Tx M .
Замечание. Дифференциал отображения в точке линеен по умножению отображения на число:
⎫⎧ ⎫ ⎧
⎫
d(a ⋅ f +b ⋅ g)⎧
⎩x⎭⎩v⎭ = v⎩a ⋅ f +b ⋅ g⎭ =
⎫
⎧ ⎫
⎧ ⎫⎧ ⎫
⎧ ⎫⎧ ⎫
= a ⋅ v⎧
⎩f⎭ + b ⋅ v⎩g⎭ = a ⋅ df⎩x⎭⎩v⎭ + b ⋅ dg⎩x⎭⎩v⎭,
где a, b ∈ R , f, g ∈ C∞ (M) , v ∈ Tx M ; а также он обладает свойством Лейбница:
⎫⎧ ⎫ ⎧ ⎫
d(f ⋅ g)⎧
⎩x⎭⎩v⎭ = v⎩f ⋅ g⎭ =
⎫ ⎧ ⎫ ⎧ ⎫ ⎧ ⎫
⎧ ⎫⎧ ⎫ ⎧ ⎫ ⎧ ⎫
⎧ ⎫⎧ ⎫
= v⎧
⎩f⎭ ⋅ g⎩x⎭ + f⎩x⎭ ⋅ v⎩g⎭ = df⎩x⎭⎩v⎭ ⋅ g⎩x⎭ + f⎩x⎭ ⋅ dg⎩x⎭⎩v⎭.
⎫
Замечание. Если f⎧
⎩ x⎭ = x
α
— α -тая координатная функция, то
>
β
⎫⎧ ⎫ ⎧ ⎫
df⎧
⎩x⎭⎩v⎭ = v⎩f⎭ = v ⋅ ∂ β x
>
>
α
>
где v ∈ Tx M и x ∈ M ; то есть dx
= v β ⋅ kronαβ = v
>
α
>
α
>
α ⎧ ⎫⎧ ⎫
⎫
= d α ∣x ⎧
⎩v⎭ = d ⎩x⎭⎩v⎭,
>
>
⎫
= d α⎧
⎩x⎭.
>
Замечание. Поэтому вычислим для произвольной гладкой функции f , предполагая v ∈ Tx M и x ∈ M :
α
α⎧ ⎫
⎫⎧ ⎫ ⎧ ⎫
⎧ ⎫
⎧ ⎫
df⎧
⎩x⎭⎩v⎭ = v⎩f⎭ = v ⋅ ∂ α f⎩x⎭ = ∂ α f⎩x⎭ ⋅ dx ⎩v⎭,
>
>
>
>
α
⎫
⎧ ⎫
то есть df⎧
⎩x⎭ = ∂ α f⎩x⎭ ⋅ dx .
>
>
Определение. Пусть задано также гладкое многообразие N размерности ν ,
а также гладкое отображение m ∈ C∞ (M, N) ; обозначим тогда дифференциал
этого отображения в точке x ∈ M по формуле
⎫⎧ ⎫⎧ ⎫ ⎧
⎫
dm⎧
⎩x⎭⎩v⎭⎩f⎭ ∶= v⎩f ○ m⎭,
f ∈ C∞ (N), v ∈ Tx M.
⎫⎧ ⎫
Часто переход v z→ dm⎧
⎩x⎭⎩v⎭ называют переносом по отображению m в
точке x .
⎫
Замечание. Нетрудно установить, что dm⎧
⎩x⎭ — линейный оператор из Tx M
в Tm⎧⎩x⎫⎭ N .
П Л, Ф,
14
Предварительные сведения и обозначения
Замечание. Если задана точка x ∈ M и отображение m ∈ C∞ (M, N) , то вычислим в локальных координатах, предполагая f ∈ C∞ (N) и v ∈ Tx M :
α
⎫⎧ ⎫⎧ ⎫ ⎧
⎫
⎧ ⎫
dm⎧
⎩x⎭⎩v⎭⎩f⎭ = v⎩f ○ m⎭ = v ⋅ ∂ α (f ○ m)⎩x⎭ =
β ⎧ ⎫
α
β ⎧ ⎫
⎧ ⎧ ⎫⎫
⎧ ⎫⎫
= v α ⋅ ∂ β f⎧
⎩m⎩x⎭⎭ ⋅ ∂ α (m )⎩x⎭ = (v ⋅ ∂ α (m )⎩x⎭) ⋅ ∂ β f⎩m⎩x⎭⎭,
>
>
>
>
>
>
>
>
>
>
β ⎧ ⎫
α
⎫⎧ ⎫ β
то есть dm⎧
⎩x⎭⎩v⎭ = ∂ α (m )⎩x⎭ ⋅ v .
>
>
>
>
γ
Определение. Пусть x ∈ M , m ∈ C∞ (M, N) , p ∈ T∗ m⎧x⎫ N ; тогда, предполагая
⎩ ⎭
γ
v1 , . . . , vγ ∈ Tx M , обозначим q ∈ T∗ x M по формуле
⎫ ∶= p⎧
⎫,
⎧ ⎫⎧ ⎫
⎧ ⎫⎧vγ ⎫
q⎧
⎪
⎪
⎩ v1 , . . . , vγ ⎪
⎭
⎩dm⎩x⎭⎩v1 ⎭, . . . , dm⎩x⎭⎪
⎩ ⎪
⎭⎪
⎭
и обозначим этот тензор
(m ↶ p) ∶= q,
x
часто называемый переносом ковариантного тензора против отображения m в
точку x .
Определение. Пусть m ∈ C∞ (M, N) , r — ковариантное тензорное поле валентности γ на многообразии N ; тогда при x ∈ M обозначим новое тензорное
поле
⎫
⎧ ⎫
(m ↶ r)⎧
⎩x⎭ ∶= (m ↶ r⎩x⎭),
⋆
x
называемое переносом ковариантного тензорного поля против отображения m .
Замечание. Очевидно, что при переносе против отображения сохраняется антисимметричность.
§5
П
В этом разделе предполагается, что задано гладкое многообразие M
размер-
ности μ .
Определение 2. Пусть на гладком многообразии M задано векторное поле v ;
тогда потоком этого поля называется гладкое по совокупности аргументов от⎫
ображение f⎧
⎩t, x⎭ со значениями во многообразии M , определенное для всех
точек x многообразия M и чисел t Ð→ 0 локально на M , являющееся решением
уравнения
⎧
α⎧ ⎧
⎫
⎫⎫
⎪
∂0 f α ⎧
⎪
⎩t, x⎭ = v ⎩f⎩t, x⎭⎭ при α = 1, . . . , μ
⎪
⎪
⎪
(1)
⎨
⎪
⎪
⎪
⎧ ⎫
⎪
⎪
⎩ f⎩0, x⎭ = x,
в котором ∂0 обозначает производную по аргументу t .
>
>
Н. С. Г, В. Л. Ч
15
Предварительные сведения и обозначения
Утверждение 3. У всякого векторного поля v на многообразии M существует
его поток f , причем он при x ∈ M и t1 , t2 Ð→ 0 обладает следующими свойствами относительно параметра:
⎧
⎫⎫ ⎧
⎫
1. f⎧
⎩t1 , f⎩t2 , x⎭⎭ = f⎩t1 + t2 , x⎭;
⎧
⎫⎫
⎧ ⎫−1 ⎧ ⎫ ⎧
⎫
2. f⎧
⎩−t1 , f⎩t1 , x⎭⎭ = x , то есть f⎩t1 , ⋅⎭ ⎩x⎭ = f⎩−t1 , x⎭
(это известно из теории обыкновенных дифференциальных уравнений).
Далее будут полезны следующие координатно-дифференциальные свойства
потока f векторного поля v на многообразии M : Замечание 4, Теорема 5, Теорема 6.
Замечание 4. Если на многообразии M задано векторное поле v с потоком f ,
β
⎫
то по определению потока верно координатное равенство f β ⎧
⎩0, x⎭ = x , и
β
β
⎫
потому ∂ α f β ⎧
⎩0, x⎭ = ∂ α x = kronα .
>
>
>
>
>
>
Теорема 5. Пусть на многообразии M задано векторное поле v с потоком f ;
тогда (в обозначениях из Определения 2)
γ⎧
β⎧ ⎧
⎫
⎫⎫
⎫
1. ∂0 ∂ α f β ⎧
⎩t, x⎭ = ∂ γ v ⎩f⎩t, x⎭⎭ ⋅ ∂ α f ⎩t, x⎭;
>
>
>
>
>
>
β⎧ ⎫
⎫
2. а при t = 0 получаем ∂0 ∂ α f β ⎧
⎩0, x⎭ = ∂ α v ⎩x⎭.
>
>
>
>
Доказательство. Продифференцируем с помощью определяющего уравнения (1):
β⎧
⎫
⎫
∂0 ∂ α f β ⎧
⎩t, x⎭ = ∂ α ∂0 f ⎩t, x⎭ =
>
>
>
>
γ⎧
β⎧ ⎧
⎧ ⎫⎫
⎫⎫
⎫
= ∂ α (v β ⎧
⎩f⎩t, x⎭⎭) = ∂ γ v ⎩f⎩t, x⎭⎭ ⋅ ∂ α f ⎩t, x⎭.
>
>
>
>
>
>
Откуда при t = 0 по Замечанию 4 получим
γ⎧
β⎧ ⎧
⎫
⎫⎫
⎫
∂0 ∂ α f β ⎧
⎩0, x⎭ = ∂ γ v ⎩f⎩0, x⎭⎭ ⋅ ∂ α f ⎩0, x⎭ =
>
>
>
>
>
>
γ
β⎧ ⎫
⎫
= ∂ γ v β⎧
⎩x⎭ ⋅ kronα = ∂ α v ⎩x⎭.⊠
>
>
>
>
Теорема 6. Пусть на многообразии M задано векторное поле v с потоком f ;
тогда
β⎧
δ⎧ ⎧
⎧ ⎫⎫
⎧ ⎫⎫
⎫⎫
1. ∂0 (∂ α f β ⎧
⎩−t, f⎩t, x⎭⎭) = − ∂ δ f ⎩−t, f⎩t, x⎭⎭ ⋅ ∂ α v ⎩f⎩t, x⎭⎭;
>
>
>
>
>
>
β⎧ ⎫
⎧ ⎫⎫
2. ∂0 (∂ α f β ⎧
⎩−t, f⎩t, x⎭⎭)∣t=0 = − ∂ α v ⎩x⎭.
>
>
>
>
П Л, Ф,
16
Предварительные сведения и обозначения
Доказательство. Продифференцируем для начала по координате левую и правую
⎧ ⎫⎫
части выражения f⎧
⎩−t, f⎩t, x⎭⎭ = x (из второго свойства Теоремы 3) в координатном виде:
β⎧
⎧ ⎫⎫
⎫
∂ α (f β ⎧
⎩−t, f⎩t, x⎭⎭) = ∂ α f ⎩−t + t, x⎭ = kronα .
>
β
>
>
>
Из этого по теореме о дифференцировании композиции получим
γ⎧
⎧ ⎫⎫
⎫
∂ γ f β⎧
⎩−t, f⎩t, x⎭⎭ ⋅ ∂ α f ⎩t, x⎭ = kronα .
β
>
>
(2)
>
>
И теперь полученное продифференцируем по аргументу t :
γ⎧
⎧ ⎫⎫
⎫
∂0 (∂ γ f β ⎧
⎩−t, f⎩t, x⎭⎭ ⋅ ∂ α f ⎩t, x⎭) =
>
>
>
>
γ⎧
⎧ ⎫⎫
⎫
= ∂0 (∂ γ f β ⎧
⎩−t, f⎩t, x⎭⎭) ⋅ ∂ α f ⎩t, x⎭+
γ⎧
⎧ ⎫⎫
⎫
+ ∂ γ f β⎧
⎩−t, f⎩t, x⎭⎭ ⋅ ∂0 ∂ α f ⎩t, x⎭ = 0,
>
>
>
>
>
>
>
>
так как в формуле (2) справа стоит постоянная.
Заменив здесь во втором слагаемом второй множитель по первой формуле
Теоремы 5, получим
γ⎧
⎧ ⎫⎫
⎫
∂0 (∂ γ f β ⎧
⎩−t, f⎩t, x⎭⎭) ⋅ ∂ α f ⎩t, x⎭+
>
>
>
>
δ⎧
γ⎧ ⎧
⎧ ⎫⎫
⎫⎫
⎫
+ ∂ γ f β⎧
⎩−t, f⎩t, x⎭⎭ ⋅ ∂ δ v ⎩f⎩t, x⎭⎭ ⋅ ∂ α f ⎩t, x⎭ = 0,
>
>
>
>
>
>
и переменим индексы суммирования:
α⎧
⎧ ⎫⎫
⎫
∂0 (∂ α f β ⎧
⎩−t, f⎩t, x⎭⎭) ⋅ ∂ γ f ⎩t, x⎭+
>
>
>
>
α⎧
δ⎧ ⎧
⎧ ⎫⎫
⎫⎫
⎫
+ ∂ δ f β⎧
⎩−t, f⎩t, x⎭⎭ ⋅ ∂ α v ⎩f⎩t, x⎭⎭ ⋅ ∂ γ f ⎩t, x⎭ = 0.
>
>
>
>
>
>
⎫ α=1,...,μ
Поскольку матрица (∂ γ f α ⎧
⎩t, x⎭)γ=1,...,μ невырождена при t Ð→ 0 , сократим на
этот общий множитель:
>
>
β⎧
δ⎧ ⎧
⎧ ⎫⎫
⎧ ⎫⎫
⎫⎫
∂0 (∂ α f β ⎧
⎩−t, f⎩t, x⎭⎭) + ∂ δ f ⎩−t, f⎩t, x⎭⎭ ⋅ ∂ α v ⎩f⎩t, x⎭⎭ = 0.
>
>
>
>
>
>
Выразив здесь первое слагаемое, получим
β⎧
δ⎧ ⎧
⎧ ⎫⎫
⎧ ⎫⎫
⎫⎫
∂0 (∂ α f β ⎧
⎩−t, f⎩t, x⎭⎭) = − ∂ δ f ⎩−t, f⎩t, x⎭⎭ ⋅ ∂ α v ⎩f⎩t, x⎭⎭.
>
>
>
>
>
>
Полагая t = 0 , по Замечанию 4 получим
⎧ ⎫⎫
∂0 (∂ α f β ⎧
⎩−t, f⎩t, x⎭⎭)∣
>
>
t=0
=
=x
>
δ⎧
=x
β⎧
δ⎧ ⎫
⎫⎫
⎧ ⎫⎫
⎫
= − ∂ δ f ⎩−0, f⎧
⎩0, x⎭⎭ ⋅ ∂ α v ⎩f⎩0, x⎭⎭ = − ∂ δ f ⎩−0, x⎭ ⋅ ∂ α v ⎩x⎭ =
β
β⎧ ⎫
⎫
= − kronδ ⋅ ∂ α v δ ⎧
⎩x⎭ = − ∂ α v ⎩x⎭.⊠
β⎧
>
>
>
>
>
>
>
>
>
Н. С. Г, В. Л. Ч
>
>
17
Предварительные сведения и обозначения
§6
Д
В
этом разделе предполагается, что задано гладкое многообразие M размерности μ .
Определение. У дифференциальных форм валентности σ = 0, . . . на многообразии M определяется внешний дифференциал — дифференциальная форма
валентности (σ + 1) — следующим индуктивным по валентности способом:
⎫⎧⎫ ⎧ ⎫
• если σ = 0 , то dp ∶= df , где p⎧
⎩x⎭⎩⎭ = f⎩x⎭,
• d(dx α ) ∶= 0,
>
∀x ∈ M ;
α = 1, . . . , μ ;
• дифференциал формы вида p1 ∧ p2 определяется по формуле
d(p1 ∧ p2 ) ∶= (dp1 ) ∧ p2 +(−1)σ ⋅ p1 ∧(dp2 ),
где σ — валентность формы p1 ;
• на дифференциальные формы — конечные суммы вышеприведенных —
дифференциал продолжается по линейности.
Теорема. Пусть p — дифференциальная форма валентности σ на многообразии M ; тогда в локальных координатах дифференциал этой формы может быть
выражен по формуле
(dp)
=
α0 ...ασ
>
δ= σ
1
σ+1
⋅ ∑ (−1)δ ⋅ ∂
αδ p >α0 ...ασ .
(3)
>
δ= 0
без αδ
Доказательство. Запишем dp через координатное представление формы p (в
этих вычислениях для краткости не пишем аргумент поля, подразумевая его
наличие):
dp = d(p
α1 ...ασ ⋅ dx
α1
>
>
∧ . . . ∧ dx
ασ
>
)=
по Определению дифференциала формы
=0
= dp
α1 ...ασ ∧ dx
>
α1
>
∧ . . . ∧ dx
ασ
>
= alt(dp
=
1
(σ + 1)!
+p
α1 ...ασ ⋅ d(dx
>α1
>
α1 ...ασ ⊗ dx
>
α1
>
⊗ . . . ⊗ dx
⋅ ∑(sign τ) ⋅ (τ ↪ (dp
τ
∧ . . . ∧ dx
ασ
>
)=
)=
α1 ...ασ ⊗ dx
>
ασ
>
α1
>
⊗ . . . ⊗ dx
(здесь и далее сумма по всем перестановкам на {1, . . . , σ + 1} );
П Л, Ф,
ασ
>
)) =
18
Предварительные сведения и обозначения
записав дифференциал координатно, перенумеруем индексы суммирования:
=
1
(σ + 1)!
=
⋅ ∑(sign τ) ⋅ (τ ↪ (∂
ασ+1 p >α1 ...ασ ⋅ dx
>
τ
1
(σ + 1)!
⋅ ∑(sign τ) ⋅ (τ ↪ (∂
ασ+1
>
α1 p >α2 ...ασ+1 ⋅ dx
α1
>
>
τ
α1
⊗ dx
>
⊗ . . . ⊗ dx
⊗ dx
α2
>
ασ
>
)) =
⊗ . . . ⊗ dx
ασ+1
>
)).
Поэтому значение дифференциала на векторных полях имеет следующий координатный вид:
dp ◂ v1 , . . . , vσ+1 =
1
(σ + 1)!
⋅ (τ ↪ (∂
1
=
(σ + 1)!
⋅ ∑(sign τ)⋅
τ
α1 p >α2 ...ασ+1 ⋅ dx
α1
>
>
α2
⊗ dx
>
⊗ . . . ⊗ dx
ασ+1
>
)) ◂ (v1 , . . . , vσ+1 ) =
⋅ ∑(sign τ)⋅
τ
⋅ (∂
α1 p >α2 ...ασ+1 ⋅ dx
α1
>
>
1
=
(σ + 1)!
⊗ dx
α2
>
⊗ . . . ⊗ dx
⋅ ∑(sign τ) ⋅ ∂
τ
ασ+1
>
) ◂ (vτ⎧⎩1⎫⎭, . . . , vτ⎧⎩σ+1⎫⎭) =
>ασ+1
>α1
α1 p >α2 ...ασ+1 ⋅ vτ⎧1⎫ ⋅ . . . ⋅ vτ⎧σ+1⎫ =;
>
⎩ ⎭
⎩
⎭
переобозначив нумерацию индексов, выделим затем первый:
=
1
(σ + 1)!
=
⋅ ∑(sign τ) ⋅ ∂
>ασ+1
>α1
ατ⎧⎩1⎫⎭ p >ατ⎧2⎫...ατ⎧σ+1⎫ ⋅ v1 ⋅ . . . ⋅ vσ+1
>
τ
β=σ+1
1
(σ + 1)!
⋅ ∑
β= 1
α
vβ β ⋅
⎩ ⎭
⎩
⎭
=
без vβ
>
∑ (sign τ) ⋅ ∂
⎫
τ∶τ⎧
⎩1⎭=β
α1
αβ p >ατ⎧2⎫...ατ⎧σ+1⎫ ⋅ v1
>
>
⎩ ⎭
⎩
⎭
1
⋅ . . . ⋅ vσα+σ+
1 =.
>
По кососимметричности формы заменив порядок нумерации индексов в ней
на возрастающий, и потом домножив на число (sign τ) ⋅ (−1)β−1 по количеству
инверсий, получим
=
β=σ+1
1
(σ + 1)!
α
>
⋅ ∑ vβ β ⋅
β= 1
∑ (sign τ) ⋅ (sign τ) ⋅ (−1)β−1 ⋅
⎫
τ∶τ⎧
⎩1⎭=β
без vβ
⋅∂
α1
αβ p >α1 ...αβ−1 αβ+1 ...ασ+1 ⋅ v1
>
>
1
⋅ . . . ⋅ vσα+σ+
1 =,
>
и после упрощения множителей знака будет
=
1
(σ + 1)!
β=σ+1
⋅ ∑
β= 1
α
vβ β ⋅(−1)β−1
>
без vβ
⋅
∑
⎫
τ∶τ⎧
⎩1⎭=β
∂ αβ p α1 ...αβ−1 αβ+1 ...ασ+1 ⋅ v1 ⋅ . . . ⋅ vσα+σ+1 1 = .
α1
>
>
>
Н. С. Г, В. Л. Ч
>
19
Предварительные сведения и обозначения
Поскольку во внутренней сумме все слагаемые (в количестве (σ!) ) одинаковы,
преобразуем:
β=σ+1
σ!
α
=
⋅ ∑ vβ β ⋅(−1)β−1 ⋅ ∂
(σ + 1)! β=1
без vβ
>
αβ p >α1 ...αβ−1 αβ+1 ...ασ+1 ⋅ v1
>
β=σ+1
1
=
α1
>
σ+1
⋅ ∑ (−1)β−1 ⋅ ∂
β= 1
1
⋅ . . . ⋅ vσα+σ+
1 =
>
>ασ+1
>α1
αβ p >α1 ...αβ−1 αβ+1 ...ασ+1 ⋅ v1 ⋅ . . . ⋅ vσ+1 .⊠
>
Теорема 7. Пусть на многообразии M задана σ -валентная дифференциальная форма p и векторные поля v0 , . . . , vσ ; тогда значение внешнего дифференциала этой формы на этих векторных полях выражается по следующей
бескоординатной формуле Картана:
δ= σ
без vδ
D
(σ + 1) ⋅ dp ◂(v0 , . . . , vσ ) = ∑ (−1)δ ⋅ vδ ▹(p ◂(v0 , . . . , vσ ))+
δ= 0
η+θ
∑ (−1)
+
0⩽η<θ⩽σ
без vη , vθ
⋅ p ◂(⟦vη , vθ ⟧ , v0 , . . . , vσ ).
Доказательство. Применив координатную формулу (3) внешнего дифференциала формы p , запишем (в этих вычислениях также для краткости не пишем
аргумент поля, подразумевая его наличие)
δ= σ
(σ + 1) ⋅ dp ◂(v0 , . . . , vσ ) = ∑ (−1)δ ⋅ ∂
>α0
>ασ
αδ p >α0 ...ασ ⋅ v0 ⋅ . . . ⋅ vσ
>
δ= 0
= (∗).
без αδ
Преобразуем обособленно слагаемое суммы (∗) с номером δ , внося произ1
1
ведение v0α0 ⋅ . . . ⋅ vδα−δ−
⋅ vδα+δ+
⋅ . . . ⋅ vσασ в производную ∂ αδ :
1
1
>
>
>
>
>
(−1)δ ⋅ ∂
>α0
>ασ
αδ p >α0 ...ασ ⋅ v0 ⋅ . . . ⋅ vσ
>
= (−1)δ ⋅ vδαδ ⋅ ∂
>
>α0
>ασ
αδ p >α0 ...ασ ⋅ v0 ⋅ . . . ⋅ vσ
>
без αδ
⎛
γ
= (−1)δ ⋅ vδ ⋅ ∂ γ ⎜p
⎝
>
>
=
без vδ
без αδ
⎞
α0
ασ
⋅
v
⋅
.
.
.
⋅
v
σ ⎟−
α0 ...ασ 0
⎠
без α
без vδ
>
>
>
δ
γ
>
− (−1)δ ⋅ vδ ⋅ p
α0 ...ασ ⋅
>
без αδ
α
>
η
α
α
∑ v0 0 ⋅ . . . ⋅ vσ σ ⋅ ∂ γ vη = ,
>
>
>
0⩽η⩽σ
без vδ , vη
η≠δ
выразив здесь первое слагаемое через бескоординатные операции, получим
⎞
D⎛
γ
= (−1)δ ⋅ vδ ▹ p ◂(v0 , . . . , vσ ) − (−1)δ ⋅ vδ ⋅ p
⎝
⎠
без v
>
δ
α0 ...ασ ⋅
>
без αδ
α
>
η
α
α
∑ v0 0 ⋅ . . . ⋅ vσ σ ⋅ ∂ γ vη .
>
>
>
0⩽η⩽σ
η≠δ
без vδ , vη
П Л, Ф,
20
Предварительные сведения и обозначения
Подставив полученное выражение в сумму (∗) , запишем
δ= σ
D
(∗) = ∑ (−1)δ ⋅ vδ ▹(p ◂(v0 , . . . , vσ ))−
δ= 0
без vδ
δ= σ
γ
>
− ∑ (−1)δ ⋅ vδ ⋅ p
δ= 0
α
>
η
α
α
∑ v0 0 ⋅ . . . ⋅ vσ σ ⋅ ∂ γ vη = (∗∗).
α0 ...ασ ⋅
>
>
>
>
0⩽η⩽σ
без αδ
без vδ , vη
η≠δ
Преобразуем вторую сумму в (∗∗) к одной общей:
δ= σ
γ
>
∑ (−1)δ ⋅ vδ ⋅ p
δ= 0
α0 ...ασ ⋅
>
без αδ
α
>
η
α
α
∑ v0 0 ⋅ . . . ⋅ vσ σ ⋅ ∂ γ vη =
>
>
>
0⩽η⩽σ
без vδ , vη
η≠δ
α
γ
>
>
= ∑ (−1)δ ⋅ vδ ⋅ ∂ γ vη η ⋅ p
>
0⩽η,δ⩽σ
>α0
>ασ
α0 ...ασ ⋅ v0 ⋅ . . . ⋅ vσ
=;
>
без vδ , vη
без αδ
η≠δ
разделив эту сумму на две отдельные при η < δ и η > δ , изменим при этом
индексы η и δ во втором случае местами:
=
α
γ
>
>
η
∑ (−1)δ ⋅ vδ ⋅ ∂ γ vη ⋅ p
>
>α0
>ασ
α0 ...ασ ⋅ v0 ⋅ . . . ⋅ vσ +
>
0⩽η<δ⩽σ
без vδ , vη
без αδ
γ
+ ∑ (−1)η ⋅ vη ⋅ ∂ γ vδαδ ⋅ p
>
>
>
0⩽η<δ⩽σ
>α0
>ασ
α0 ...ασ ⋅ v0 ⋅ . . . ⋅ vσ
=,
>
без vδ , vη
без αη
и перейдем к одной сумме с выделением общего множителя:
=
α
α
∑ v0 0 ⋅ . . . ⋅ vσ σ ⋅
>
0⩽η<δ⩽σ
>
без vδ , vη
α
γ
>
>
⋅ ((−1)δ ⋅ vδ ⋅ ∂ γ vη η ⋅ p
>
η
α0 ...ασ +(−1)
>
γ
⋅ vη ⋅ ∂ γ vδαδ ⋅ p
>
>
>
α0 ...ασ )
>
без αδ
= (∗ ∗ ∗).
без αη
Отдельно преобразуем стоящий в скобках множитель из (∗ ∗ ∗) , изменяя
знаки по кососимметричности формы p (с учетом η < δ ):
α
γ
>
>
(−1)δ ⋅ vδ ⋅ ∂ γ vη η ⋅ p
>
η
α0 ...ασ +(−1)
>
γ
⋅ vη ⋅ ∂ γ vδαδ ⋅ p
>
>
>
α0 ...ασ
>
без αδ
без αη
β
γ
>
>
=
= (−1)δ ⋅ vδ ⋅ ∂ γ vη ⋅(−1)η ⋅ p
>
η
βα0 ...ασ +(−1)
>
β
γ
⋅ vη ⋅ ∂ γ vδ ⋅(−1)δ−1 ⋅ p
>
>
>
без αδ , αη
= (−1)η+δ ⋅ p
=
без αδ , αη
>β
>β
>γ
>γ
βα0 ...ασ ⋅ (vδ ⋅ ∂ >γ vη − vη ⋅ ∂ >γ vδ )
>
без αδ , αη
βα0 ...ασ
>
= (−1)η+δ ⋅ p
=
β
>
βα0 ...ασ ⋅ ⟦vδ , vη ⟧ .
>
без αδ , αη
Н. С. Г, В. Л. Ч
21
Предварительные сведения и обозначения
Подставив (∗ ∗ ∗) в (∗∗) с учетом последней формулы, преобразуем к
бескоординатному виду:
δ= σ
D
(∗∗) = ∑ (−1)δ ⋅ vδ ▹(p ◂(v0 , . . . , vσ ))−
δ= 0
без vδ
− ∑ v0α0 ⋅ . . . ⋅ vσασ ⋅(−1)η+δ ⋅ p
>
0⩽η<δ⩽σ
δ= σ
>
без vδ , vη
βα0 ...ασ ⋅ ⟦vδ , vη ⟧
>
β
>
=
без αδ , αη
D
= ∑ (−1)δ ⋅ vδ ▹(p ◂(v0 , . . . , vσ ))+
δ= 0
без vδ
+ ∑ (−1)η+δ ⋅ p ◂ (⟦vη , vδ ⟧ , v0α0 ⋅ . . . ⋅ vσασ ) . ⊠
>
0⩽η<δ⩽σ
>
без vδ , vη
П Л, Ф,
22
Построение производной Ли
2. Построение производной Ли
§7
П
Л
Рассмотрим
гладкое многообразие M размерности μ и векторное поле j
⎫
на нем; поток этого поля обозначим k⎧
⎩t, x⎭, где x ∈ M , а t — параметр на
траектории решения системы
⎧
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎩
⎫ α ⎧ ⎧ ⎫⎫
∂0 k α ⎧
⎩t, x⎭ = j ⎩k⎩t, x⎭⎭ при α = 1, . . . , μ
>
>
(4)
⎫
k⎧
⎩0, x⎭ = x,
в котором ∂0 обозначает производную по аргументу t .
Определение. Пусть задана гладкая функция f на многообразии M ; обозначим тогда ее перенос j À f = g векторным полем j по формуле
⎫ ⎧ ⎫ ⎧ ⎧ ⎫⎫
(j À f)⎧
⎩t, y⎭ = g⎩t, y⎭ ∶= f⎩k⎩t, y⎭⎭.
⎫
В этой формуле задается «перенос» значения функции f из точки x = k⎧
⎩t, y⎭ в
⎫
точку y = k⎧
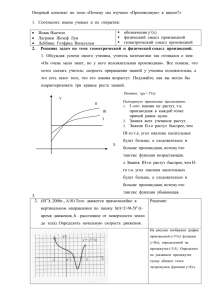
⎩−t, x⎭ (см. рис. {1}).
Определение. Пусть теперь задано векторное поле u на многообразии M ; обозначим тогда его перенос j À u = v векторным полем j по формуле
⎫ ⎧ ⎫
⎧
⎧ ⎫⎫⎧ ⎧ ⎧ ⎫⎫⎫
(j À u)⎧
⎩t, y⎭ = v⎩t, y⎭ ∶= dk⎩−t, k⎩t, y⎭⎭⎩u⎩k⎩t, y⎭⎭⎭.
В локальных координатах эта формула имеет вид
α⎧
⎫
⎧ ⎫⎫ β ⎧ ⎧ ⎫⎫
v α⎧
⎩t, y⎭ ∶= ∂ β k ⎩−t, k⎩t, y⎭⎭ ⋅ u ⎩k⎩t, y⎭⎭.
>
>
>
>
(5)
Как и при переносе числовой функции, здесь задается «перенос» значения
⎫
⎧
⎫
векторного поля u из точки x = k⎧
⎩t, y⎭ в точку y = k⎩−t, x⎭ (см. рис. {1}).
Определение. Наконец, пусть на многообразии M задано δ -валентное ковариантное тензорное поле p (в частности, дифференциальная δ -форма); обозначим
тогда его перенос j À p = q векторным полем j по формуле
⎫ ⎧ ⎫
⎧ ⎫
⎧ ⎫ ⎧ ⎫
⎧ ⎧ ⎫⎫
(j À p)⎧
⎩t, y⎭ = q⎩t, y⎭ ∶= (k⎩t, ⋅⎭ ↶ p)⎩y⎭ = k⎩t, ⋅⎭ ↶ p⎩k⎩t, y⎭⎭.
⋆
y
В локальных координатах эта формула имеет вид
q
⎧
⎫
α1 ,...,αδ ⎩t, y⎭ ∶=
>
β ⎧
⎫
⎫
⎧ ⎧ ⎫⎫
∂ α1 k β1 ⎧
⎩t, y⎭ ⋅ . . . ⋅ ∂ αδ k δ ⎩t, y⎭ ⋅ p β1 ,...,βδ ⎩k⎩t, y⎭⎭.
>
>
>
>
Н. С. Г, В. Л. Ч
>
(6)
23
Построение производной Ли
⎫
f⎧
⎩x⎭
⎫
g⎧
⎩t, y⎭
g
f
y
x
⎫
u⎧
⎩x⎭
⎫
v⎧
⎩t, y⎭
Рис. 1: Переносы векторным полем функции и векторного поля.
⎫
Здесь также задан «перенос» значения тензорного поля p из точки x = k⎧
⎩t, y⎭
⎫
в точку y = k⎧
⎩−t, x⎭.
Отметим дополнительно, что непосредственным расчетом устанавливается согласованность всех трех вышеопределенных переносов друг с другом в смысле
коммутирования переноса и операции вычисления значения ковариантного
тензорного поля на векторных полях; это значит, что для векторных полей
u1 , . . . , uδ и ковариантного тензорного поля p валентности δ выполнена формула
⎧ ⎫⎫
⎫
⎧ ⎫⎧
⎧ ⎫
(j À f)⎧
⎩t, y⎭ = (j À p)⎩t, y⎭⎩(j À u1 )⎩t, y⎭, . . . , (j À uδ )⎩t, y⎭⎭,
⎫ ⎧ ⎫⎧ ⎧ ⎫
⎧ ⎫⎫
где обозначено f⎧
⎩x⎭ = p⎩x⎭⎩u1 ⎩x⎭, . . . , uδ ⎩x⎭⎭.
Далее заметим, что перенос векторным полем вводит внешний параметр,
и может быть определена скорость переноса относительно этого параметра в
начальный момент (при t = 0 ). Ясно при этом, что скорость переноса есть
поле того же типа, что и подвергнутое переносу. А поскольку скорость есть
производная, ее так и называют — производная Ли (по имени математика
Софуса Ли). Ниже определим эту производную более формально.
⎫
Определение. Для гладкой функции f на многообразии M , обозначив g⎧
⎩t, y⎭ ∶=
⎫
= (j À f)⎧
⎩t, y⎭, определим также гладкую функцию Lj f = h — производную Ли
П Л, Ф,
24
Построение производной Ли
гладкой функции f векторным полем j по формуле
⎧ ⎫ ⎧ ⎫
⎧ ⎫ ⎧ ⎫
⎫ ∶= ∂0 g⎧0, y⎫ = lim g⎩t, y⎭ − g⎩0, y⎭ = lim g⎩t, y⎭ − f⎩y⎭.
h⎧
y
⎩ ⎭
⎩ ⎭ tÐ→0
tÐ→0
t
t
(7)
⎫
Определение. Для векторного поля u на многообразии M , обозначив v⎧
⎩t, y⎭ ∶=
⎫
(j À u)⎧
⎩t, y⎭, определим также векторное поле Lj u = w — производную Ли
векторного поля u векторным полем j по формуле
v⎧
t, y⎫
− v⎧
0, y⎫
v⎧
t, y⎫
− u⎧
y⎫
⎩
⎭
⎩
⎭
⎩
⎭
⎩
⎭.
⎧
⎫
⎧
⎫
w⎩y⎭ ∶= ∂0 v⎩0, y⎭ = lim
= lim
tÐ→0
tÐ→0
t
t
(8)
Предел здесь понимается в смысле обычной сходимости в конечномерном
пространстве — касательной плоскости к точке y .
Определение 8. Наконец, для δ -валентного ковариантного тензорного поля p
⎫
⎧ ⎫
на многообразии M , обозначив q⎧
⎩t, y⎭ ∶= (j À p)⎩t, y⎭, определим δ -валентное
ковариантное тензорное поле Lj p = r — производную Ли δ -валентного ковариантного тензорного поля p векторным полем j по формуле
⎧ ⎫ ⎧ ⎫
⎧ ⎫ ⎧ ⎫
⎫ ∶= ∂0 q⎧0, y⎫ = lim q⎩t, y⎭ − q⎩0, y⎭ = lim q⎩t, y⎭ − p⎩y⎭.
r⎧
y
⎩ ⎭
⎩ ⎭ tÐ→0
tÐ→0
t
t
(9)
И здесь предел понимается в смысле обычной сходимости в конечномерном
пространстве соответствующих тензоров в точке.
Еще раз укажем, что по этим определениям все пределы дают тензоры того же
типа, что и исходные; а гладкость сохранится по причине гладкости (бесконечной непрерывной дифференцируемости) исходных зависимостей.
§8
К
При
решении задач с вовлечением производной Ли полезно иметь ее координатное выражение; установим здесь его, предполагая как и в разделе
определения производной Ли, что заданы гладкое многообразие M размерности
⎫
μ и векторное поле j на нем, поток которого обозначен k⎧
⎩t, x⎭.
Теорема. Пусть задана гладкая функция f на многообразии M ; тогда ее
производная Ли векторным полем j — гладкая функция Lj f = h , вычисляемая в
локальных координатах по формуле
⎫ α⎧ ⎫
⎧ ⎫
h⎧
⎩y⎭ = j ⎩y⎭ ⋅ ∂ α f⎩y⎭.
>
>
(10)
Доказательство. Вычислим из формул (4) и (7), дифференцируя сложную функН. С. Г, В. Л. Ч
25
Построение производной Ли
цию:
⎫
⎧ ⎫
⎧ ⎧ ⎫⎫
h⎧
⎩y⎭ ∶= ∂0 g⎩0, y⎭ = ∂0 (f⎩k⎩t, y⎭⎭)∣t=0 =
α⎧
⎧ ⎫⎫
⎫
= ∂ α f⎧
⎩k⎩t, y⎭⎭∣t=0 ⋅ ∂0 k ⎩t, y⎭∣t=0 =
>
>
⎫
⎧ ⎫
= j α⎧
⎩y⎭ ⋅ ∂ α f⎩y⎭,
>
>
α⎧
⎫
⎫ α ⎧ ⎧ ⎫⎫
поскольку k⎧
⎩0, y⎭ = y и ∂0 k ⎩t, y⎭ = j ⎩k⎩t, y⎭⎭. ⊠
Теорема. Пусть задано векторное поле u на многообразии M ; тогда его производная Ли векторным полем j — векторное поле Lj u = w , вычисляемое в
локальных координатах по формуле
>
>
α⎧ ⎫
α⎧ ⎫
β⎧ ⎫
⎫ β⎧ ⎫
w α⎧
⎩y⎭ = j ⎩y⎭ ⋅ ∂ β u ⎩y⎭ − u ⎩y⎭ ⋅ ∂ β j ⎩y⎭.
>
>
>
>
>
>
(11)
>
Доказательство. Продифференцируем по формулам (8) и (5):
α⎧
α⎧
⎫
⎫
⎧ ⎫⎫ β ⎧ ⎧ ⎫⎫
w α⎧
⎩y⎭ = ∂0 v ⎩0, y⎭ = ∂0 (∂ β k ⎩−t, k⎩t, y⎭⎭ ⋅ u ⎩k⎩t, y⎭⎭)∣t=0 =
β⎧ ⎧
⎧ ⎫⎫
⎫⎫
= ∂0 (∂ β k α ⎧
⎩−t, k⎩t, y⎭⎭)∣t=0 ⋅ u ⎩k⎩0, y⎭⎭+
β⎧ ⎧
⎧ ⎫⎫
⎫⎫
+ ∂ β k α⎧
⎩0, k⎩0, y⎭⎭ ⋅ ∂0 (u ⎩k⎩t, y⎭⎭)∣t=0 =,
>
>
>
>
>
>
>
>
>
>
>
применив здесь второее свойство из Теоремы 6 к первому сомножителю первого слагаемого, а ко второму сомножителю второго слагаемого — теорему о
производной композиции, получим
= kronαβ
⎫
= j γ⎧
⎩ y⎭
>
=y
α⎧
γ⎧
β⎧ ⎧
⎫
⎫⎫
⎫
⎫ β⎧ ⎫
= − ∂ β j α⎧
⎩y⎭ ⋅ u ⎩y⎭ + ∂ β k ⎩0, y⎭ ⋅ ∂ γ u ⎩k⎩0, y⎭⎭ ⋅ ∂0 k ⎩0, y⎭ =
α
β⎧ ⎫ γ⎧ ⎫
⎫ β⎧ ⎫
= − ∂ β j α⎧
⎩y⎭ ⋅ u ⎩y⎭ + kronβ ⋅ ∂ γ u ⎩y⎭ ⋅ j ⎩y⎭ =
α⎧ ⎫
α⎧ ⎫
β⎧ ⎫
⎫
= j β⎧
⎩y⎭ ⋅ ∂ β u ⎩y⎭ − u ⎩y⎭ ⋅ ∂ β j ⎩y⎭. ⊠
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
Теорема. Пусть задано δ -валентное ковариантное тензорное поле p на многообразии M ; тогда его производная Ли векторным полем j — δ -валентное
ковариантное тензорное поле Lj p = r , вычисляемое в локальных координатах
по формуле
r
⎧ ⎫ j β ⎧ y⎫ ⋅ ∂ β p
⎩ ⎭
α1 ,...,αδ ⎩y⎭ =
>
>
>
⎧ ⎫
α1 ,...,αδ ⎩y⎭+
η=δ
>
+∑p
η=1
⎧ ⎫
α1 ,...,αη−1 ,β,αη+1 ,...,αδ ⎩y⎭ ⋅ ∂ >αη j
>
β⎧
>
⎫
⎩y⎭. (12)
Доказательство. Продифференцируем по формулам (9) и (6):
r
⎧ ⎫
⎧
⎫
α1 ,...,αδ ⎩y⎭ = ∂0 q >α1 ,...,αδ ⎩0, y⎭ =
>
>β
⎫
⎧ ⎫
⎧ ⎧ ⎫⎫
= ∂0 (∂ >α1 k β1 ⎧
⎩t, y⎭ ⋅ . . . ⋅ ∂ >αδ k δ ⎩t, y⎭ ⋅ p >β1 ,...,βδ ⎩k⎩t, y⎭⎭)∣
>
П Л, Ф,
t=0
=
26
Построение производной Ли
как производная произведения
=∂
α1 k
>
β1 ⎧
>
⎫
⎩0, y⎭ ⋅ . . . ⋅ ∂
η=δ
+∑p
η=1
αδ k
>
βδ ⎧
>
⎫
⎩0, y⎭ ⋅ ∂0 (p
⎧ ⎫
β1 ,...,βδ ⎩y⎭ ⋅ ∂ >α1 k
>
⋅ ∂0 ∂
αη k
>
β1 ⎧
>
⎫
⎩0, y⎭ ⋅ . . . ⋅ ∂
βη ⎧
>
⎧ ⎧
⎫
⎩0, y⎭ ⋅ ∂
⎫⎫
β1 ,...,βδ ⎩k⎩t, y⎭⎭)∣t=0 +
>
αη+1 k
>
αη−1 k
>
βη+1 ⎧
>
βη−1 ⎧
>
⎫
⎩0, y⎭⋅
⎫
⎩0, y⎭ ⋅ . . . ⋅ ∂
αδ k
>
βδ ⎧
>
⎫
⎩0, y⎭ =,
применим здесь Замечание 4 и второе свойства из Теоремы 5 и, упростив,
получим
β
β
= kronα11 ⋅ . . . ⋅ kronαδδ ⋅ ∂ γ p
>
η=δ
+∑p
η=1
γ⎧
>
⎫
⎩0, y⎭+
βη+1
βη−1
βδ
β1
>β
⎧ ⎫
η⎧ ⎫
β1 ,...,βδ ⎩y⎭ ⋅ kronα1 ⋅ . . . ⋅ kronαη−1 ⋅ ∂ >αη j ⎩y⎭ ⋅ kronαη+1 ⋅ . . . ⋅ kronαδ
>
β⎧
= j ⎩ y⎫
⎭⋅ ∂ β p
>
§9
⎧ ⎫
β1 ,...,βδ ⎩y⎭ ⋅ ∂0 k
>
>
η=δ
⎧ ⎫
α1 ,...,αδ ⎩y⎭ + ∑ p
>
η=1
⎧ ⎫
α1 ,...,αη−1 ,β,αη+1 ,...,αδ ⎩y⎭ ⋅ ∂ >αη j
>
=
β⎧
>
⎫
⎩y⎭. ⊠
Б
Установим в этом разделе бескоординатное представление производной Ли,
а также правило Лейбница, предполагая как и в разделе определения производной Ли, что заданы гладкое многообразие M размерности μ и векторное поле j
на нем.
Замечание 9. Из определения 8 очевидно следует, что для ковариантного
тензорного поля
• коммутируют его производная Ли и перестановка его аргументов —
векторных полей;
• а если это поле есть дифференциальная форма, то по перестановочности
внешнего дифференцирования и переноса формы против отображения ее
производная Ли и внешнее дифференцирование также перестановочны.
Теорема. Пусть на многообразии M заданы гладкая функция f и векторное
поле u ; тогда их производные Ли векторным полем j имеют вид
D
L j f = h = j ▹ f,
Lj u = w = ⟦j, u⟧ ;
Н. С. Г, В. Л. Ч
27
Построение производной Ли
а если на многообразии M задано δ -валентное ковариантное тензорное поле p
и u1 , . . . , uδ — векторные поля, то значение на них тензорного поля Lj p = r
вычисляется по следующей бескоординатной формуле:
D
r ◂(u1 , . . . , uδ ) = (Lj p) ◂ (u1 , . . . , uδ ) = j ▹ (p ◂(u1 , . . . , uδ )) −
η=δ
− ∑ p ◂(u1 , . . . , uη−1 , ⟦j, uη ⟧ , uη+1 , . . . , uδ ). (13)
η=1
Доказательство. Вид производных гладкой функции и векторного поля следуют
из формул (10) и (11).
В случае же ковариантного поля p проведем расчет значения в локальных коор⎫
динатах, применив формулу (12) (для краткости не будем писать аргумент ⎧
⎩ y⎭
отображений, подразумевая при этом его наличие):
⎫ β
(r ◂(u1 , . . . , uδ ))⎧
⎩ y⎭ = j ⋅ ∂ β p
>
>
>α
>α1
δ
α1 ,...,αδ ⋅ u1 ⋅ . . . ⋅ uδ +
η=δ
>
+∑p
η=1
α1 ,...,αη−1 ,β,αη+1 ,...,αδ ⋅ ∂ >αη j
β
>
>
⋅ u1α1 ⋅ . . . ⋅ uδαδ =
>
>
добавим и вычтем слагаемые, чтобы сформировать производную векторным
полем j функции p ◂(u1 , . . . , uδ ) :
= j β⋅∂ βp
>α
>α1
δ
α1 ,...,αδ ⋅ u1 ⋅ . . . ⋅ uδ +
>
>
η=δ
+∑j
>
αη
>
η=1
η=δ
−∑j
αη
>
η=1
>αη−1
>αη+1
>β
>α
>α1
δ
α1 ,...,αη−1 ,β,αη+1 ,...,αδ ⋅ u1 ⋅ . . . ⋅ uη−1 ⋅ ∂ >αη uη ⋅ uη+1 ⋅ . . . ⋅ uδ −
⋅p
>
⋅p
>
>αη−1
>αη+1
>β
>α
>α1
δ
α1 ,...,αη−1 ,β,αη+1 ,...,αδ ⋅ u1 ⋅ . . . ⋅ uη−1 ⋅ ∂ >αη uη ⋅ uη+1 ⋅ . . . ⋅ uδ +
η=δ
+∑p
η=1
α1 ,...,αη−1 ,β,αη+1 ,...,αδ ⋅ ∂ >αη j
>
β
>
⋅ u1α1 ⋅ . . . ⋅ uδαδ =
>
>
из слагаемых двух первых строк формируем производную векторным полем j
функции p ◂(u1 , . . . , uδ ) , а последние две суммы запишем в одной сумме:
η=δ
D
= j ▹ (p ◂(u1 , . . . , uδ )) + ∑ p
η=1
⋅ (− j
αη
>
α
>
α1 ,...,αη−1 ,β,αη+1 ,...,αδ ⋅
>
1
⋅ u1α1 ⋅ . . . ⋅ uη−η−
1 ⋅∂
>
>αη+1
>β
>α
>α
>α1
>β
δ
δ
αη uη ⋅ uη+1 ⋅ . . . ⋅ uδ + ∂ >αη j ⋅ u1 ⋅ . . . ⋅ uδ )
>
П Л, Ф,
=
28
Построение производной Ли
в сумме обособим общие сомножители и перейдем к коммутатору:
η=δ
D
= j ▹ (p ◂(u1 , . . . , uδ )) + ∑ p
η=1
α
α1 ,...,αη−1 ,β,αη+1 ,...,αδ ⋅
>
α
1
η+1
αδ
⋅ u1α1 ⋅ . . . ⋅ uη−η−
1 ⋅ uη+1 ⋅ . . . ⋅ uδ ⋅(− j
>
>
>
>
αη
>
⋅∂
>αη
>β
>β
αη uη + ∂ >αη j ⋅ uη )
>
=
η=δ
D
= j ▹ (p ◂(u1 , . . . , uδ )) − ∑ (p ◂(u1 , . . . , uη−1 , ⟦j, uη ⟧ , uη+1 , . . . , uδ )) . ⊠
η=1
Следствие. Если u — векторное поле, то производная Ли тензорного
γ
поля p ←
Ð u вычисляется по аналогу правила Лейбница:
γ
γ
γ
γ
γ
Lj (p ←
Ð u) = ((Lj p) ←
Ð u) + (p ←
Ð (Lj u)) = ((Lj p) ←
Ð u) + (p ←
Ð ⟦j, u⟧) ;
(14)
также при γ = 1 это может быть выражено через внутреннее дифференцирование:
Lj (u ⌟ p) = ((Lj u) ⌟ p) + (u ⌟(Lj p)) = (⟦j, u⟧ ⌟ p) + (u ⌟(Lj p)) .
(15)
Доказательство. Вычислим значение левого тензорного поля из формулы (14)
на векторных полях u1 , . . . , uγ−1 , uγ+1 , . . . , uδ :
γ
Ð u)) ◂ (u1 , . . . , uγ−1 , uγ+1 , . . . , uδ ) =
(Lj (p ←
γ
D
= j ▹ ((p ←
Ð u) ◂ (u1 , . . . , uγ−1 , uγ+1 , . . . , uδ )) −
η=γ−1
γ
Ð u) ◂ (u1 , . . . , uη−1 , ⟦j, uη ⟧ , uη+1 , . . . , uγ−1 , uγ+1 , . . . , uδ )−
− ∑ (p ←
η=1
η=δ
γ
Ð u) ◂ (u1 , . . . , uγ−1 , uγ+1 , . . . , uη−1 , ⟦j, uη ⟧ , uη+1 , . . . , uδ ) =
− ∑ (p ←
η=γ+1
внесем поле u в ряд аргументов поля p :
D
= j ▹ (p ◂(u1 , . . . , uγ−1 , u, uγ+1 , . . . , uδ )) −
η=γ−1
− ∑ p ◂(u1 , . . . , uη−1 , ⟦j, uη ⟧ , uη+1 , . . . , uγ−1 , u, uγ+1 , . . . , uδ )−
η=1
η=δ
− ∑ p ◂(u1 , . . . , uγ−1 , u, uγ+1 , . . . , uη−1 , ⟦j, uη ⟧ , uη+1 , . . . , uδ ) =,
η=γ+1
обозначив uγ ∶= u для единообразия слагаемых с нумерованными полями,
Н. С. Г, В. Л. Ч
Построение производной Ли
29
вычтем и добавим слагаемое p ◂(u1 , . . . , uγ−1 , ⟦j, uγ ⟧ , uγ+1 , . . . , uδ ) :
D
= j ▹ (p ◂(u1 , . . . , uγ−1 , u, uγ+1 , . . . , uδ )) −
η=γ−1
− ∑ p ◂(u1 , . . . , uη−1 , ⟦j, uη ⟧ , uη+1 , . . . , uγ−1 , u, uγ+1 , . . . , uδ )−
η=1
− p ◂(u1 , . . . , uγ−1 , ⟦j, uγ ⟧ , uγ+1 , . . . , uδ )−
η=δ
− ∑ p ◂(u1 , . . . , uγ−1 , u, uγ+1 , . . . , uη−1 , ⟦j, uη ⟧ , uη+1 , . . . , uδ )+
η=γ+1
+ p ◂(u1 , . . . , uγ−1 , ⟦j, uγ ⟧ , uγ+1 , . . . , uδ ) =
заметив, что в первых четырех строках этой формулы стоит производная Ли
поля p , и оба полученных слагаемых выражаются через подстановку γ -того
аргумента, запишем итоговое выражение:
= (Lj p) ◂ (u1 , . . . , uγ−1 , u, uγ+1 , . . . , uδ )+
+ p ◂(u1 , . . . , uγ−1 , ⟦j, uγ ⟧ , uγ+1 , . . . , uδ ) =
γ
= ((Lj p) ←
Ð u) ◂ (u1 , . . . , uγ−1 , uγ+1 , . . . , uδ )+
γ
+ (p ←
Ð ⟦j, u⟧) ◂ (u1 , . . . , uγ−1 , uγ+1 , . . . , uδ ). ⊠
Следствие. Пусть на многообразии M заданы δ1 -валентное ковариантное
тензорное поле p1 и δ2 -валентное ковариантное тензорное поле p2 ; тогда
Lj (p1 ⊗ p2 ) = (Lj p1 ) ⊗ p2 + p1 ⊗ (Lj p2 ) .
(16)
Доказательство. Предположив, что на многообразии M заданы векторные поля u1 , . . . , uδ1 +δ2 , запишем по формуле (13):
(Lj (p1 ⊗ p2 )) ◂ (u1 , . . . , uδ1 +δ2 ) =
D
= j ▹ ((p1 ⊗ p2 ) ◂ (u1 , . . . , uδ1 +δ2 )) −
η=δ1 +δ2
− ∑ (p1 ⊗ p2 ) ◂ (u1 , . . . , uη−1 , ⟦j, uη ⟧ , uη+1 , . . . , uδ1 +δ2 ) =,
η=1
распределив слагаемые суммы по номерам в диапазонах валентностей тензоров,
и представив значение тензорного произведения как произведение значений,
П Л, Ф,
30
Построение производной Ли
получим
D
= j ▹ ((p1 ◂(u1 , . . . , uδ1 )) ⋅ (p2 ◂(uδ1 +1 , . . . , uδ1 +δ2 ))) −
η=δ1
− ∑ (p1 ◂(u1 , . . . , uη−1 , ⟦j, uη ⟧ , uη+1 , . . . , uδ1 )) ⋅ (p2 ◂(uδ1 +1 , . . . , uδ1 +δ2 )) −
η=1
η=δ1 +δ2
− ∑ (p1 ◂(u1 , . . . , uδ1 )) ⋅ (p1 ◂(uδ1 +1 , . . . , uη−1 , ⟦j, uη ⟧ , uη+1 , . . . , uδ1 +δ2 )) =,
η=1+δ1
применив правило Лейбница к первому выражению и переменив места слагаемых, получим
D
= (j ▹ (p1 ◂(u1 , . . . , uδ1 ))) ⋅ (p2 ◂(uδ1 +1 , . . . , uδ1 +δ2 )) −
η=δ1
− ∑ (p1 ◂(u1 , . . . , uη−1 , ⟦j, uη ⟧ , uη+1 , . . . , uδ1 )) ⋅ (p2 ◂(uδ1 +1 , . . . , uδ1 +δ2 )) +
η=1
D
+ (p1 ◂(u1 , . . . , uδ1 )) ⋅ (j ▹ (p2 ◂(uδ1 +1 , . . . , uδ1 +δ2 ))) −
η=δ1 +δ2
− ∑ (p1 ◂(u1 , . . . , uδ1 )) ⋅ (p1 ◂(uδ1 +1 , . . . , uη−1 , ⟦j, uη ⟧ , uη+1 , . . . , uδ1 +δ2 )) =,
η=1+δ1
выделив общие множители в первых двух и последних двух слагаемых, получим
по формуле (13)
= ((Lj p1 ) ◂ (u1 , . . . , uδ1 )) ⋅ (p2 ◂(uδ1 +1 , . . . , uδ1 +δ2 )) +
+ (p1 ◂(u1 , . . . , uδ1 )) ⋅ ((Lj p2 ) p2 ◂(uδ1 +1 , . . . , uδ1 +δ2 )) =
= ((Lj p1 ) ⊗ p2 ) ◂ (u1 , . . . , uδ1 +δ2 ) + (p1 ⊗ (Lj p2 )) ◂ (u1 , . . . , uδ1 +δ2 ) =
= ((Lj p1 ) ⊗ p2 + p1 ⊗ (Lj p2 )) ◂ (u1 , . . . , uδ1 +δ2 ). ⊠
Следствие. Из Замечания 9 и формулы (16) по линейности следует, что если
на многообразии M заданы δ1 -валентная дифференциальная форма p1 и δ2 валентная дифференциальная форма p2 , то
Lj (p1 ∧ p2 ) = (Lj p1 ) ∧ p2 + p1 ∧ (Lj p2 ) .
§ 10
И
С
В
этом разделе покажем связь производной Ли дифференциальной формы
с внешним и внутренним дифференцированиями, предполагая как и в разделе
определения производной Ли, что заданы гладкое многообразие M размерности
μ и векторное поле v на нем.
Н. С. Г, В. Л. Ч
31
Построение производной Ли
Теорема. Пусть на многообразии M задана дифференциальная форма p валентности α ; тогда выполняется инфинитезимальная формула Стокса:
Lv p = v ⌟ dp + d(v ⌟ p).
(17)
Доказательство. Предположив, что на многообразии M заданы векторные поля w1 , . . . , wα , запишем по формуле Картана (см. Теорему 7) значение формы v ⌟ dp на них (поле v соответствует в ней полю w0 ):
(v ⌟ dp) ◂ (w1 , . . . , wα ) = (α + 1) ⋅ dp ◂(v, w1 , . . . , wα ) =
δ= α
D
D
без wδ
= (−1) ⋅ v ▹ (p ◂(w1 , . . . , wα )) + ∑ (−1)δ ⋅ wδ ▹ (p ◂(v, w1 , . . . , wα )) +
0
δ= 1
γ=α
+ ∑ (−1)0+γ ⋅ p ◂(⟦v, wγ ⟧ , w1 , . . . , wα )+
γ=1
без wγ
β+γ
+
∑ (−1)
1⩽β<γ⩽α
без wβ , wγ
⋅ p ◂(⟦wβ , wγ ⟧ , v, w1 , . . . , wα ) =,
переставив в третьем слагаемом коммутатор с первой позиции на γ -тую (и
потому домножив по кососимметричности формы на число (−1)γ−1 по числу
транспозиций при этой перестановке), переставив затем третье слагаемое со
вторым, и в последнем слагаемом переставив ⟦wβ , wγ ⟧ и v (и потому изменив
знак этого слагаемого), получим
D
= v ▹ (p ◂(w1 , . . . , wα )) +
γ=α
+ ∑ (−1)0+γ ⋅ (−1)γ−1 ⋅ p ◂(w1 , . . . , wγ−1 , ⟦v, wγ ⟧ , wγ+1 , . . . , wα )+
γ=1
δ= α
D
+ ∑ (−1)δ ⋅ wδ ▹ (p ◂(v, w1 , . . . , wα )) +
δ= 1
без wδ
β+γ
+
∑ (−1)
1⩽β<γ⩽α
без wβ , wγ
⋅ (−1) ⋅ p ◂(v, ⟦wβ , wγ ⟧ , w1 , . . . , wα ) =,
поскольку первое и второе слагаемые образуют производную Ли формы p , а в
третьем и четвертом слагаемых поле v стоит на первых позициях, соответствуя
внутреннему дифференциалу той же формы, перепишем
= (Lv p) ◂ (w1 , . . . , wα ) −
−
1
α
⋅
1
α
∑
δ=α−1
D
без wδ+1
⋅ ∑ (−1)δ ⋅ wδ+1 ▹ ((v ⌟ p) ◂ (w1 , . . . , wα )) −
δ= 0
0⩽β<γ⩽α−1
β+γ+2
(−1)
без wβ+1 , wγ+1
⋅ (v ⌟ p) ◂ (⟦wβ+1 , wγ+1 ⟧ , w1 , . . . , wα ) =
П Л, Ф,
32
Построение производной Ли
заметив наконец, что последние две суммы образуют внешний дифференциал
формы v ⌟ p , перепишем
= (Lv p) ◂ (w1 , . . . , wα ) − d(v ⌟ p) ◂ (w1 , . . . , wα ). ⊠
Следствие. Пусть на многообразии M задана дифференциальная форма p
валентности α , а также векторное поле w ; тогда выполняется формула
w ⌟(v ⌟ dp) = (w ∧ v) ⌟ dp = Lv (w ⌟ p) − w ⌟ d(v ⌟ p) + ⟦w, v⟧ ⌟ p .
Доказательство. Применим формулу (15):
Lv (w ⌟ p) = ⟦v, w⟧ ⌟ p + w ⌟(Lv p) =
применим инфинитезимальную формулу Стокса (17):
= ⟦v, w⟧ ⌟ p + w ⌟(v ⌟ dp + d(v ⌟ p)) =
= ⟦v, w⟧ ⌟ p + w ⌟(v ⌟ dp) + w ⌟ d(v ⌟ p).
Выразив же здесь w ⌟(v ⌟ dp) , получим заявленное. ⊠
Следствие. В частности, в случае валентности 1 получим формулу
D
2 ⋅ dp ◂(v, w) = v ▹(p ◂ w) − d(p ◂ v) ◂ w + p ◂ ⟦w, v⟧ =
= d(p ◂ w) ◂ v − d(p ◂ v) ◂ w + p ◂ ⟦w, v⟧ =
D
D
= v ▹(p ◂ w) − w ▹(p ◂ v) + p ◂ ⟦w, v⟧ . (18)
Н. С. Г, В. Л. Ч
33
Теорема Фробениуса
3. Теорема Фробениуса
§ 11
Л
В
этом разделе предполагается, что задано гладкое многообразие M размерности μ .
Лемма. Пусть на многообразии задано векторное поле v с его потоком
k (см. обозначения в Определении 2); тогда если u — векторное поле на
многообразии, а ∂0 — обозначение производной по t в точке x ∈ M , то при
t Ð→ 0 верно
⎧
⎫⎫⎧ ⎧ ⎧
⎫⎫⎫
⎧ ⎧
⎫⎫⎧
⎧ ⎧
⎫⎫⎫
∂0 (dk⎧
⎩t, k⎩−t, x⎭⎭⎩u⎩k⎩−t, x⎭⎭⎭) = − dk⎩t, k⎩−t, x⎭⎭⎩⟦v, u⟧⎩k⎩−t, x⎭⎭⎭,
что в координатах соответствует формуле
⎧
⎫⎫ β ⎧ ⎧
⎫⎫
∂0 (∂ β k α ⎧
⎩t, k⎩−t, x⎭⎭ ⋅ u ⎩k⎩−t, x⎭⎭) =
>
>
>
β⎧ ⎧
⎧
⎫⎫
⎫⎫
= − ∂ β k α⎧
⎩t, k⎩−t, x⎭⎭ ⋅ ⟦v, u⟧ ⎩k⎩−t, x⎭⎭.
>
>
>
Доказательство. Продифференцируем левую часть координатного равенства:
⎧
⎫⎫ β ⎧ ⎧
⎫⎫
∂0 (∂ β k α ⎧
⎩t, k⎩−t, x⎭⎭ ⋅ u ⎩k⎩−t, x⎭⎭) =
>
>
>
β⎧ ⎧
⎧
⎫⎫
⎫⎫
= ∂0 (∂ β k α ⎧
⎩t, k⎩−t, x⎭⎭) ⋅ u ⎩k⎩−t, x⎭⎭+
β⎧ ⎧
⎧
⎫⎫
⎫⎫
+ ∂ β k α⎧
⎩t, k⎩−t, x⎭⎭ ⋅ ∂0 (u ⎩k⎩−t, x⎭⎭) =,
>
>
>
>
>
>
применив теорему о производной композиции ко второму сомножителю второго
слагаемого, получим
β⎧ ⎧
⎧
⎫⎫
⎫⎫
= ∂0 (∂ β k α ⎧
⎩t, k⎩−t, x⎭⎭) ⋅ u ⎩k⎩−t, x⎭⎭+
>
>
>
⎧
⎫⎫
= v γ⎧
⎩k⎩−t, x⎭⎭
>
γ⎧ ⎧
β⎧ ⎧
⎫⎫
⎧
⎫⎫
⎫⎫
+ ∂ β k α⎧
⎩t, k⎩−t, x⎭⎭ ⋅ ∂ γ u ⎩k⎩−t, x⎭⎭ ⋅ ∂0 k ⎩k⎩−t, x⎭⎭⋅(−1) =;
>
>
>
>
>
после применения к первому сомножителю первого слагаемого первого равенства Теоремы 6 будет
γ⎧ ⎧
⎧
⎫⎫
⎫⎫ β ⎧ ⎧
⎫⎫
= ∂ γ k α⎧
⎩t, k⎩−t, x⎭⎭ ⋅ ∂ β v ⎩k⎩−t, x⎭⎭ ⋅ u ⎩k⎩−t, x⎭⎭+
β⎧ ⎧
⎧
⎫⎫
⎫⎫ γ ⎧ ⎧
⎫⎫
+ ∂ β k α⎧
⎩t, k⎩−t, x⎭⎭ ⋅ ∂ γ u ⎩k⎩−t, x⎭⎭ ⋅ v ⎩k⎩−t, x⎭⎭ ⋅ (−1) = .
>
>
>
>
>
>
>
>
>
>
С помощью замены индексов и выделения общего множителя формула преобразуется к
γ⎧ ⎧
⎧
⎫⎫
⎫⎫ β ⎧ ⎧
⎫⎫
= ∂ γ k α⎧
⎩t, k⎩−t, x⎭⎭ ⋅ (∂ β v ⎩k⎩−t, x⎭⎭ ⋅ u ⎩k⎩−t, x⎭⎭+
>
>
>
>
>
⎧
⎫⎫ β ⎧ ⎧
⎫⎫
+ ∂ β u γ⎧
⎩k⎩−t, x⎭⎭ ⋅ v ⎩k⎩−t, x⎭⎭ ⋅ (−1)) =,
>
>
>
П Л, Ф,
34
Теорема Фробениуса
и после замены выражения в скобках по формуле коммутатора получим
γ⎧ ⎧
⎧
⎫⎫
⎫⎫
= − ∂ γ k α⎧
⎩t, k⎩−t, x⎭⎭ ⋅ ⟦v, u⟧ ⎩k⎩−t, x⎭⎭. ⊠
>
>
>
Лемма 10. Пусть на многообразии задано векторное поле v с его потоком k ;
тогда если u1 , . . . , uσ — векторные поля на многообразии такие, что коммутатор
каждого из них с полем v есть линейная комбинация полей u1 , . . . , uσ с
зависящимим от точки коэффициентами, то при x ∈ M , t Ð→ 0 , α = 1, . . . , σ
параметрические векторные поля
⎫
⎧ ⎧
⎫⎫⎧ ⎧ ⎧
⎫⎫⎫
wα ⎧
⎩t, x⎭ ∶= dk⎩t, k⎩−t, x⎭⎭⎩uα ⎩k⎩−t, x⎭⎭⎭
также суть линейные комбинации полей u1 , . . . , uσ , но с коэффициентами,
зависящими от точки и параметра.
Доказательство. Вычислим производную этих полей по t , применяя предыдущую Лемму:
γ
α⎧
⎫
⎧
⎫⎫
⎧ ⎧
⎫⎫
∂0 wβα ⎧
⎩t, x⎭ = − ∂ γ k ⎩t, k⎩−t, x⎭⎭ ⋅ ⟦v, uβ ⟧ ⎩k⎩−t, x⎭⎭ =;
>
>
>
>
заменив коммутаторы на их линейные выражения через поля u1 , . . . , uσ с
⎫
коэффициентами fδβ ⎧
⎩x⎭, получим
⎧
⎫⎫ δ ⎧ ⎧
⎫⎫ γ ⎧ ⎧
⎫⎫
= − ∂ γ k α⎧
⎩t, k⎩−t, x⎭⎭ ⋅ fβ ⎩k⎩−t, x⎭⎭ ⋅ uδ ⎩k⎩−t, x⎭⎭ =
α⎧
⎧
⎫⎫
⎧
⎫⎫ γ ⎧ ⎧
⎫⎫
= − fδβ ⎧
⎩k⎩−t, x⎭⎭ ⋅ (∂ γ k ⎩t, k⎩−t, x⎭⎭ ⋅ uδ ⎩k⎩−t, x⎭⎭) =
⎧
⎫⎫ α ⎧ ⎫
= − fδβ ⎧
⎩k⎩−t, x⎭⎭ ⋅ wδ ⎩t, x⎭.
>
>
>
>
>
>
>
Заметим, что эта совокупность уравнений есть система линейных однородных дифференциальных уравнений первого порядка относительно функций
⎫
⎧ ⎫
w1 ⎧
⎩⋅, x⎭, . . . , wσ ⎩⋅, x⎭ при постоянной точке x .
По теореме Коши о существовании решения дифференциального уравнения
первого порядка найдется решение этой системы в линейной оболочке векторов
⎫
⎧ ⎫
⎧ ⎫
⎧ ⎫
w1 ⎧
⎩0, x⎭ = u1 ⎩x⎭, . . . , wσ ⎩0, x⎭ = uσ ⎩x⎭
(линейном подпространстве пространства Tx M ); и по той же теореме решение
это единственно и во всем пространстве Tx M .
⎫
⎧ ⎫
⎧ ⎫
Итак, векторы wβ ⎧
⎩t, x⎭ суть линейные комбинации векторов u1 ⎩x⎭, . . . , uσ ⎩x⎭
с коэффициентами, зависящими от t . ⊠
Н. С. Г, В. Л. Ч
35
Теорема Фробениуса
Лемма 11. Пусть на многообразии заданы векторные поля u1 , . . . , uμ с линейно независимыми значениями в каждой точке, а также выбраны потоки
k1 , . . . , kμ этих полей; тогда если x ∈ M , то отображение
1
μ⎫
⎧ t1 , ⋅ ⎫
⎧ μ ⎫⎧ ⎫
m⎧
⎪
⎩t , . . . , t ⎪
⎭ ∶= (k1 ⎪
⎩ ⎪
⎭ ○ . . . ○ kμ ⎩t , ⋅⎭)⎩x⎭
есть биекция некоторой окрестности нуля в Rμ и некоторой окрестности точки
⎫
x = m⎧
⎩0, . . . , 0⎭; при этом набор частных производных этого отображения по
его переменным имеет ранг μ в точках окрестности.
Доказательство. Обозначим индуктивно точки:
⎧
⎪
⎪
⎪ yμ ∶= x
⎨
⎪
⎧α ⎫
⎪
⎪
⎩ yα−1 ∶= kα ⎩t , yα ⎭, α = μ, . . . , 1.
Вычислим производную:
1
μ⎫
⎧ t1 , y ⎫
∂1 m⎧
⎪
1⎪
⎩t , . . . , t ⎪
⎭ = ∂0 k1 ⎪
⎩
⎭,
и если 1 < γ ⩽ μ, то
1
μ⎫
∂γ m⎧
⎪
⎩t , . . . , t ⎪
⎭= ∂
⎧ t1 , y ⎫
α2 k1 ⎪
1⎪
⎩
⎭⋅ ∂
>
⋅ ... ⋅ ∂
(19)
α2 ⎧ 2
>
α3 k2
>
⎫⋅
⎪
⎩ t , y2 ⎪
⎭
>αγ−1 ⎧
>αγ ⎧
⎫
⎫
γ−1
γ
⎪
⎪
t
,
y
t
,
y
⋅
∂
⎪
⎪
⎪
⎪
αγ kγ−1 ⎪
0 kγ ⎪
γ
−
1
γ
⎩
⎩
⎭
⎭.
>
Подставив t1 = . . . = tμ = 0 в эти выражения, по Замечанию 4 и определяющему
уравнению потока (1) получим y0 = . . . = yμ = x и
⎫
∂γ m⎧
⎩0, . . . , 0⎭ =
⎧
⎫
⎪
∂0 k1 ⎧
при γ = 1
⎪
⎩0, x⎭
⎪
⎪
⎪
⎪
⎪
= ⎨ ∂ α2 k1 ⎧0, x⎫ ⋅ ∂ α3 k2α2 ⎧0, x⎫⋅
⎩ ⎭
⎩ ⎭
⎪
⎪
⎪
⎪
α 1⎧
⎪
αγ ⎧
⎪
⎫
⎫ при 1 < γ ⩽ μ.
⎪
⋅ . . . ⋅ ∂ αγ kγ−γ−
1 ⎩0, x⎭ ⋅ ∂0 kγ ⎩0, x⎭
⎩
>
>
>
>
>
>
⎫
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎬=
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎭
⎫
= uγ ⎧
⎩x⎭.
Поэтому из условия Леммы следует, что векторы
⎫
⎧
⎫
∂0 m⎧
⎩0, . . . , 0⎭, . . . , ∂μ m⎩0, . . . , 0⎭
линейно независимы; и тем самым отображение m биективно на некоторой
окрестности нуля в Rμ , а векторы его частных производных линейно независимы на этой окрестности. ⊠
П Л, Ф,
36
Теорема Фробениуса
Лемма 12. Пусть на многообразии заданы векторные поля u1 , . . . , uμ с линейно независимыми значениями в каждой точке, а коммутатор всяких двух полей из u1 , . . . , uσ (при σ ⩽ μ ) есть линейная комбинация этих полей u1 , . . . , uσ с
зависящимим от точки коэффициентами; тогда если выбраны потоки k1 , . . . , kμ
этих полей, x ∈ M и отображение m построено по формуле из предыдущей
Леммы, то векторные поля
μ ⎧ ⎫⎫
⎫
⎧ 1⎧ ⎫
wγ ⎧
⎩y⎭ ∶= ∂γ m⎩g ⎩y⎭, . . . , g ⎩y⎭⎭ при γ = 1, . . . , σ
суть также линейные комбинации полей u1 , . . . , uσ с зависящимим от точки
коэффициентами, где функции gα такие, что
⎧ t1 , . . . , tμ ⎫
⎫ = tα
gα ⎧
⎪
⎪
⎩ m⎪
⎩
⎭⎪
⎭
при γ = 1, . . . , μ ,
существуют по предыдущей Лемме и теореме о неявном отображении.
Доказательство. Пусть точка y = y0 из окрестности точки x ; и определим тогда
⎧ γ
⎫
⎫
⎪ при γ > 0 .
параметры tα ∶= gα ⎧
⎪
⎩y⎭, и точки yγ ∶= kγ ⎪
⎩−t , yγ−1 ⎪
⎭
⎫
Подставив эти значения в формулу (19), получим выражение полей wγ ⎧
⎩y⎭:
⎫
⎧ ⎫
w1 ⎧
⎩y⎭ = u1 ⎩y⎭,
и если γ > 1, то
⎧ γ−1
⎫
⎫
⎧ t1 , y ⎫
⎫
⎪)⎧
⎪ uγ ⎧
⎪yγ−1 ⎫
⎪
⎪.
wγ ⎧
⎪
⎪
1⎪
⎩y⎭ = (dk1 ⎪
⎩
⎭ ○ . . . ○ dkγ−1 ⎪
⎩t , yγ−1 ⎪
⎭⎪
⎩ ⎪
⎩
⎭⎪
⎭
По Лемме 10 при 1 < γ ⩽ σ векторное поле
⎧ γ−1
⎫
⎫
⎪⎧
⎪ uγ ⎧
⎪yγ−1 ⎫
⎪
⎪=
dkγ−1 ⎪
⎪
⎪
⎩t , yγ−1 ⎪
⎭⎪
⎩ ⎪
⎩
⎭⎪
⎭
⎧ γ−1
⎧
⎫
⎫
γ−1
⎪−tγ−1 , yγ−2 ⎫
⎪
⎪⎧
⎪ uγ ⎧
⎪kγ−1 ⎧
⎪
⎪⎫
⎪⎫
⎪
= dkγ−1 ⎪
⎪
⎪
⎪
⎩t , kγ−1 ⎪
⎩
⎭⎪
⎭⎪
⎩ ⎪
⎩
⎩−t , yγ−2 ⎪
⎭⎪
⎭⎪
⎭
есть линейная комбинация полей u1 , . . . , uσ .
Таким образом последовательно применяя ту же Лемму с учетом линейности
дифференциала, получим заявленное в утверждении. ⊠
§ 12
Р
Ф
В
этом разделе предполагается, что задано гладкое многообразие M размерности μ .
Рассмотрим на многообразии некоторые векторные поля с линейно независимыми значениями в каждой точке; выберем также некоторую точку многообразия.
Н. С. Г, В. Л. Ч
Теорема Фробениуса
37
Составим в некоторых локальных координатах вокруг выбранной точки матрицу координат значений этих полей. Заметив, что по линейной независимости
значений векторных полей ее ранг максимален, дополним затем ее до квадратной невырожденной в окрестности выбранной точки.
Ясно, что дополняющие столбцы можно считать координатами дополнительных
векторных полей; и тем самым исходные поля можно дополнить в окрестности выбранной точки до набора векторных полей с линейно независимыми
значениями в каждой точке в числе размерности многообразия.
Замечание 13. Итак, если на многообразии заданы векторные поля u1 , . . . , uσ с
линейно независимыми значениями в каждой точке, и выбрана также некоторая
точка многообразия, то найдется окрестность выбранной точки и векторные
поля uσ+1 , . . . , uμ на этой окрестности такие, что векторные поля u1 , . . . , uμ
также с линейно независимыми значениями в каждой точке этой окрестности.
Определение. Отображение Z , действующее на некотором открытом подмножестве D многообразия M , и сопоставляющее каждой точке x этого
⎫
множества некоторое линейное подпространство Z⎧
⎩x⎭ касательного пространства Tx M , называется распределением размерности σ на множестве D , если
для каждой точки x ∈ D найдется окрестность ее во множестве D и набор
векторных полей u1 , . . . , uσ на той окрестности такие, что для всякой точки
⎫
y из той окрестности пространство Z⎧
⎩y⎭ есть линейная оболочка векторов
⎫
⎧ ⎫
u1 ⎧
⎩y⎭, . . . , uσ ⎩y⎭ и эти векторы линейно независимы; поля же эти векторные
называются локальным базисом распределения.
Определение. Пусть на открытом подмножестве D многообразия задано
распределение Z ; тогда векторное поле v на этом множестве D называется
⎫
сечением распределения Z , если для каждой точки x ∈ D вектор v⎧
⎩x⎭ принад⎫
лежит пространству Z⎧
⎩x⎭.
Определение. Распределение Z размерности σ на открытом подмножестве D многообразия называется вполне интегрируемым, если для всякой точки x из множества D найдется окрестность этой точки во множестве D
и гладкие функции g1 , . . . , gμ−σ на той окрестности такие, что для всякой
⎫
точки y из той окрестности и всякого вектора w из пространства Z⎧
⎩ y⎭
⎫⎧ ⎫
выполнено dgα ⎧
⎩y⎭⎩w⎭ = 0 при α = 1, . . . , μ − σ , а кокасательные векторы
μ−σ ⎧ ⎫
⎫
dg1 ⎧
⎩y⎭, . . . , dg ⎩y⎭ линейно независимы.
Определение. Распределение называется инволютивным, если только коммутатор всяких его двух сечений есть его же сечение.
П Л, Ф,
38
Теорема Фробениуса
Лемма 14. Распределение инволютивно, если и только если для всякой точки
найдется локальный базис распределения на окрестности этой точки такой, что
коммутатор всяких двух полей из этого базиса есть линейная комбинация его
полей с коэффициентами, зависящими от точки.
Доказательство. Из инволютивности распределения следует заявленное свойство базиса.
⎫
⎧ ⎫
Если же u1 , . . . , uσ — локальный базис распределения, а fα ⎧
⎩ x⎭ ⋅ u α ⎩ x⎭ и
⎫ ⎧ ⎫
hα ⎧
⎩x⎭⋅ uα ⎩x⎭ — локальное разложение сечений распределения, то вычислим их
коммутатор:
γ
>
γ
γ
⟦fα ⋅ uα , hβ ⋅ uβ ⟧ = fα ⋅ uαδ ⋅ ∂ δ (hβ ⋅ uβ ) − hβ ⋅ uβδ ⋅ ∂ δ (fα ⋅ uα ) =
>
>
>
>
>
>
по правилу Лейбница
γ
γ
γ
γ
= fα ⋅ uαδ ⋅ (∂ δ hβ ⋅ uβ + hβ ⋅ ∂ δ uβ ) − hβ ⋅ uβδ ⋅ (∂ δ fα ⋅ uα + fα ⋅ ∂ δ uα ) = .
>
>
>
>
>
>
>
>
>
>
Раскрыв скобки, получим
γ
γ
= fα ⋅ uαδ ⋅ ∂ δ hβ ⋅ uβ + fα ⋅ uαδ ⋅ hβ ⋅ ∂ δ uβ −
>
>
>
>
>
>
γ
γ
− hβ ⋅ uβδ ⋅ ∂ δ fα ⋅ uα − hβ ⋅ uβδ ⋅ fα ⋅ ∂ δ uα =
>
>
>
>
>
>
после перемещения слагаемых и группировки
γ
γ
γ
γ
= fα ⋅ uαδ ⋅ ∂ δ hβ ⋅ uβ − hβ ⋅ uβδ ⋅ ∂ δ fα ⋅ uα + fα ⋅ hβ ⋅ (uαδ ⋅ ∂ δ uβ − uβδ ⋅ ∂ δ uα ) =,
>
>
>
>
>
>
>
>
>
>
>
>
переменив индексы и выделив общий множитель, получим
γ
γ
>
= uβδ ⋅ uα ⋅ (fβ ⋅ ∂ δ hα − hβ ⋅ ∂ δ fα ) + fα ⋅ hβ ⋅ ⟦uα , uβ ⟧ .
>
>
>
>
Обе части последнего выражения суть линейные комбинации полей из локального базиса распределения. ⊠
Лемма. Пусть на множестве D задано распределение Z размерности σ ;
тогда если оно вполне интегрируемо, то оно инволютивно.
Доказательство. Возьмем два сечения u и v распределения Z ; рассмотрим
некоторую точку x из D с ее окрестностью в этом множестве, и гладкие
функции g1 , . . . , gμ−σ такие, что для всякой точки y из той окрестности и
α ⎧ ⎫⎧ ⎫
⎫
всякого вектора w из пространства Z⎧
⎩y⎭ выполнено dg ⎩y⎭⎩w⎭ = 0 при
μ−σ ⎧ ⎫
⎫
α = 1, . . . , μ − σ , и кокасательные векторы dg1 ⎧
⎩y⎭, . . . , dg ⎩y⎭ линейно независимы.
Н. С. Г, В. Л. Ч
39
Теорема Фробениуса
Вычислим:
D
u ▹ gα = dgα ◂ u = 0,
D
v ▹ gα = dgα ◂ v = 0,
по выбору функций g1 , . . . , gμ−σ .
И поэтому
D
D
D
D
D
dgα ◂ ⟦u, v⟧ = ⟦u, v⟧ ▹ gα = u ▹(v ▹ gα ) − v ▹(u ▹ gα ) = 0.
⎫
Из этого и соотношения σ + (μ − σ) = μ размерностей следует ⟦u, v⟧⎧
⎩ x⎭ ∈
⎫
∈ Z⎧
⎩x⎭. ⊠
Лемма. Пусть на множестве D задано распределение Z размерности σ ;
тогда если оно инволютивно, то оно вполне интегрируемо.
Доказательство. Выберем некоторый локальный базис u1 , . . . , uσ распределения
Z на некоторой окрестности некоторой точки x .
По Замечанию 13 дополним на некоторой подокрестности точки x эти векторные поля до набора u1 , . . . , uμ с линейно независимыми значениями в точках.
Выбрав некоторые потоки этих векторных полей, построим из них отображение
m по формуле из Леммы 11 для точки x .
По Лемме 11 найдутся функции g1 , . . . , gμ на окрестности точки x такие,
⎧ t1 , . . . , tμ ⎫
⎫ = tα при α = 1, . . . , μ .
что gα ⎧
⎪
⎪
⎩ m⎪
⎩
⎭⎪
⎭
Обозначим векторные поля
μ ⎧ ⎫⎫
⎫
⎧ 1⎧ ⎫
wα ⎧
⎩y⎭ ∶= ∂α m⎩g ⎩y⎭, . . . , g ⎩y⎭⎭ при α = 1, . . . , μ .
При α, β = 1, . . . , μ вычислим:
μ ⎧ ⎫⎫⎧ α ⎫
⎧ ⎫⎧ α ⎫
⎧ 1⎧ ⎫
⎫⎧wβ ⎧y⎫⎫
dgα ⎧
⎩y⎭⎪
⎭ = wβ ⎩y⎭⎩g ⎭ = ∂β m⎩g ⎩y⎭, . . . , g ⎩y⎭⎭⎩g ⎭ =
⎩ ⎩ ⎭⎪
α
α
1⎧ ⎫
μ ⎧ ⎫⎫
= ∂β (gα ○ m)⎧
⎩g ⎩y⎭, . . . , g ⎩y⎭⎭ = ∂β t ∣tα =gα ⎧⎩y⎫⎭ = kronβ .
В частности, dgα ◂ wβ = 0 при α = σ + 1, . . . , μ и β = 1, . . . , σ .
⎫
⎧ ⎫
Поскольку по Леммам 11 и 12 векторы w1 ⎧
⎩y⎭, . . . , wσ ⎩y⎭ линейно независимы
⎫
⎧ ⎫
и выражаются линейно через векторы u1 ⎧
⎩y⎭, . . . , uσ ⎩y⎭, эти векторные поля
w1 , . . . , wσ суть локальный базис распределения Z .
⎫⎧ ⎫
⎧ ⎫
Поэтому dgα ⎧
⎩y⎭⎩w⎭ = 0 для всякого вектора w ∈ Z⎩y⎭.
П Л, Ф,
40
Теорема Фробениуса
μ⎧ ⎫
⎫
По Лемме 11 ковекторы dgσ+1 ⎧
⎩y⎭, . . . , dg ⎩y⎭ линейно независимы.
Итак, распределение Z вполне интегрируемо. ⊠
Из последних двух Лемм следует критерий вполне интегрируемости.
Теорема Фробениуса. Пусть на множестве D задано распределение Z ; тогда
оно вполне интегрируемо, если только оно инволютивно.
§ 13
И
В
этом разделе предполагается, что задано гладкое многообразие M размерности μ .
Определение. Пусть на некотором открытом множестве заданы одновалентные дифференциальные формы p1 , . . . , pτ , а также некоторое распределение
Z размерности σ ; тогда набор p1 , . . . , pτ сопряжен с распределением Z , если
только
• σ + τ = μ;
• формы p1 , . . . , pτ линейно независимы в каждой точке того открытого
множества;
• для всякого сечения v распределения Z верно pα ◂ v = 0 при α = 1, . . . , τ .
Определение. Пусть на некотором открытом множестве заданы одновалентные дифференциальные формы p1 , . . . , pτ ; тогда набор p1 , . . . , pτ дифференциально линейно зависим, если только найдутся одновалентные дифференциальные
формы qαβ при α, β = 1, . . . , τ такие, что dpα = qαβ ∧ pβ при α = 1, . . . , τ .
Лемма. Пусть на некоторой окрестности некоторой точки многообразия M
задано распределение Z , а также задан сопряженный с ним набор p1 , . . . , pτ
одновалентных дифференциальных форм; тогда если распределение Z инволютивно, то набор p1 , . . . , pτ дифференциально линейно зависим.
Доказательство. По теореме Фробениуса на некоторой окрестности той же
точки существуют гладкие функции g1 , . . . , gτ такие, что набор dg1 , . . . , dgτ
сопряжен с распределением Z .
Поэтому на некоторой окрестности той же точки найдутся гладкие функции
fαβ при α, β = 1, . . . , τ такие, что pα = fαβ ⋅ dgβ при α = 1, . . . , τ ; и аналогично
найдутся гладкие функции hαβ при α, β = 1, . . . , τ такие, что dgα = hαβ ⋅ pβ при
α = 1, . . . , τ .
Н. С. Г, В. Л. Ч
41
Теорема Фробениуса
Следовательно
β
β
dpα = dfαβ ∧ dgβ = dfαβ ∧ hγ ⋅ pγ = (hγ ⋅ dfαβ ) ∧ pγ . ⊠
Лемма. Пусть на некоторой окрестности некоторой точки многообразия M
задано распределение Z , а также задан сопряженный с ним набор p1 , . . . , pτ
одновалентных дифференциальных форм; тогда если набор p1 , . . . , pτ дифференциально линейно зависим, то распределение Z инволютивно.
Доказательство. По определению дифференциальной линейной зависимости
найдутся одновалентные дифференциальные формы qαβ при α, β = 1, . . . , τ
такие, что dpα = qαβ ∧ pβ при α = 1, . . . , τ .
Выбрав два сечения v и w распределения Z , вычислим:
dpα ◂(v, w) = (qαβ ∧ pβ ) ◂ (v, w) =
=
1
⋅ ((qαβ ◂ v) ⋅ (∧ pβ ◂ w) − (qαβ ◂ w) ⋅ (∧ pβ ◂ v)) = 0
2
при α = 1, . . . , τ .
С другой стороны по формуле (18)
α
D
=0
α
=0
α
2 ⋅ dp ◂(v, w) = v ▹(p ◂ w) − d(p ◂ v) ◂ w + pα ◂ ⟦w, v⟧ = pα ◂ ⟦w, v⟧
при α = 1, . . . , τ .
Следовательно pα ◂ ⟦w, v⟧ = 0 при α = 1, . . . , τ ; откуда ⟦w, v⟧ есть сечение
распределения Z . ⊠
Лемма. Пусть на некоторой окрестности некоторой точки многообразия M
задан набор p1 , . . . , pτ одновалентных дифференциальных форм; тогда если
набор p1 , . . . , pτ дифференциально линейно зависим, то dpα ∧ p1 ∧ . . . ∧ pτ = 0
при α = 1, . . . , τ .
Доказательство. По определению дифференциальной линейной зависимости
найдутся одновалентные дифференциальные формы qαβ при α, β = 1, . . . , τ
такие, что dpα = qαβ ∧ pβ при α = 1, . . . , τ .
Вычислим:
dpα ∧ p1 ∧ . . . ∧ pτ = qαβ ∧ pβ ∧ p1 ∧ . . . ∧ pτ = 0
при α = 1, . . . , τ , ибо каждое слагаемое содержит два одинаковых сомножителя. ⊠
Лемма. Пусть на некоторой окрестности некоторой точки многообразия
M задан набор p1 , . . . , pτ поточечно линейно независимых одновалентных
П Л, Ф,
42
Теорема Фробениуса
дифференциальных форм; тогда если dpα ∧ p1 ∧ . . . ∧ pτ = 0 при α = 1, . . . , τ ,
то набор p1 , . . . , pτ дифференциально линейно зависим.
Доказательство. Дополним набор p1 , . . . , pτ до базисного (то есть до размерности μ ) формами pτ+1 , . . . , pμ .
Ясно, что форма dpα есть линейная комбинация произведений pβ ∧ pγ ; и
если бы при β, γ > τ коэффициенты были ненулевые, то и произведение
dpα ∧ p1 ∧ . . . ∧ pτ было бы ненулевое, что не верно. ⊠
Из последних четырех Лемм следует критерий инволютивности (и вполне
интегрируемости).
Теорема. Пусть на некоторой окрестности некоторой точки многообразия M
задано распределение Z , а также задан сопряженный с ним набор p1 , . . . , pτ
одновалентных дифференциальных форм; тогда распределение Z инволютивно,
если только dpα ∧ p1 ∧ . . . ∧ pτ = 0 при α = 1, . . . , τ .
Н. С. Г, В. Л. Ч
43
Разбор примеров / Дифференциальные формы
4. Разбор примеров
4.1. Дифференциальные формы
§ 14
В
Задание 1. Пусть на некотором двумерном многообразии задана дифференциальная форма p валентности 1 , выраженная в локальных координатах по
формуле
1
2
2
1
⎫
p⎧
⎩x⎭ = x ⋅ dx + 2 ⋅ x ⋅ dx ,
>
>
>
>
а в точке y с координатами y 1 = 1 и y 2 = 2 задан вектор v с координатами
⎫⎧ ⎫
v 1 = 3 и v 2 = 4 ; вычислить значение p⎧
⎩y⎭⎩v⎭ дифференциальной формы p в
точке y на касательном векторе v в той же точке.
>
>
>
>
Решение. Напомним, что дифференциальная форма есть отображение, сопоставляющее каждой точке некоторого открытого подмножества многообразия
кокасательный вектор в той точке (то есть вещественнозначное линейное отображение на касательном пространстве к этой точке), причем в координатном
выражении этой зависимости коэффициенты бесконечно дифференцируемы.
Для вычисления искомого значения следует определить координатное выраже⎫
ние кокасательного вектора p⎧
⎩y⎭ — значения дифференциальной формы p в
точке y — путем подстановки значений координат точки y в выражение формы
p . А затем вычислить сумму призведений координат этого кокасательного
⎫
вектора p⎧
⎩y⎭ и вектора v с одинаковыми номерами.
Итак, следуя указанному плану, вычислим вначале форму p в точке y :
1
2
2
1
2
1
⎫
p⎧
⎩y⎭ = y ⋅ dy + 2 ⋅ y ⋅ dy = 1 ⋅ dy + 2 ⋅ 2 ⋅ dy .
>
>
>
>
>
>
И теперь вычислим искомое:
2⎧ ⎫
1⎧ ⎫
⎫⎧ ⎫
p⎧
⎩y⎭⎩v⎭ = 1 ⋅ dy ⎩v⎭ + 2 ⋅ 2 ⋅ dy ⎩v⎭ =
= 1 ⋅ v 2 +2 ⋅ 2 ⋅ v 1 = 1 ⋅ 4 + 2 ⋅ 2 ⋅ 3 = 16.
>
>
>
>
⎫⎧ ⎫
Ответ. Итак, p⎧
⎩y⎭⎩v⎭ = 16 . ⊠
Задание 2. Пусть на некотором двумерном многообразии задана дифференциальная форма p валентности 1 , выраженная в локальных координатах по
формуле
1
2
2
1
⎫
p⎧
⎩x⎭ = x ⋅ dx + 2 ⋅ x ⋅ dx ,
>
>
>
>
П Л, Ф,
44
Разбор примеров / Дифференциальные формы
а также задано векторное поле u с координатным выражением
1
2
⎫
u 1⎧
⎩ x⎭ = x + x ,
1
2
⎫
u 2⎧
⎩ x⎭ = x − x ;
>
>
>
>
>
>
вычислить координатное выражение гладкой функции p ◂ u — значения формы
p на векторном поле u .
Решение. Вычисление сводится к определению значения кокасательного вектора
⎫
⎧ ⎫
p⎧
⎩x⎭ на касательном векторе u⎩x⎭ при произвольной точке x .
Вычислим:
⎫ ⎧ ⎫⎧ ⎧ ⎫⎫
(p ◂ u)⎧
⎩x⎭ = p⎩x⎭⎩u⎩x⎭⎭ =
1⎧ ⎧ ⎫⎫
2⎧ ⎧ ⎫⎫
⎫
⎧ ⎫
= p 1⎧
⎩x⎭ ⋅ dx ⎩u⎩x⎭⎭ + p 2 ⎩x⎭ ⋅ dx ⎩u⎩x⎭⎭ =
⎫ 1⎧ ⎫
⎧ ⎫ 2⎧ ⎫
= p 1⎧
⎩x⎭ ⋅ u ⎩x⎭ + p 2 ⎩x⎭ ⋅ u ⎩x⎭ =;
>
>
>
>
>
>
>
>
подставим координатные выражения формы p и векторного поля u :
= 2 ⋅ x 2 ⋅ (x 1 + x 2 ) + x 1 ⋅ (x 1 − x 2 ) = (x 1 )2 + x 1 ⋅ x 2 + 2 ⋅ (x 2 )2 .
>
>
>
>
>
>
>
>
>
>
1 2
1
2
2 2
⎫
Ответ. Итак, (p ◂ u)⎧
⎩x⎭ = (x ) + x ⋅ x + 2 ⋅ (x ) . ⊠
>
>
>
>
Задание 3. Пусть теперь задана дифференциальная форма q валентности 2
с координатным выражением
1
2
1
⎫
q⎧
⎩x⎭ = x ⋅ dx ∧ dx ,
>
>
>
и в точке y с координатами y 1 = 1 и y 2 = 2 заданы вектор v с координатами
v 1 = 3 , v 2 = 4 и вектор w с координатами w 1 = 2 , w 2 = 3 ; вычислить значение
⎫⎧
⎫
q⎧
⎩y⎭⎩v, w⎭ формы q в точке y на векторах v, w .
>
>
>
>
>
>
Решение. По указанному ранее плану вычислим вначале форму q в точке y :
1
2
1
2
1
⎫
q⎧
⎩y⎭ = y ⋅ dx ∧ dx = 1 ⋅ dx ∧ dx =
>
>
>
>
>
=
1
⋅ (dx 2 ⊗ dx 1 − dx 1 ⊗ dx 2 ) ;
2
>
>
>
>
и по определению тензорного произведения вычислим искомое значение, подставив координаты векторов:
2 ⎧
1
1
2
⎫⎧
⎫ 1
⎫
q⎧
⎩y⎭⎩v, w⎭ = 2 ⋅ (dx ⊗ dx − dx ⊗ dx )⎩v, w⎭ =
=
>
>
>
>
1
1
1
1
⋅ (v 2 ⋅ w 1 − v 1 ⋅ w 2 ) = ⋅ (4 ⋅ 2 − 3 ⋅ 3) = ⋅ (−1) = − .
2
2
2
2
>
>
>
>
Н. С. Г, В. Л. Ч
45
Разбор примеров / Дифференциальные формы
1
⎫⎧
⎫
Ответ. Итак, q⎧
⎩y⎭⎩v, w⎭ = − 2 . ⊠
Задание 4. Вычислить значение u ⌟ q внутренней производной формы q
валентности 2 с координатным выражением
1
2
⎫
q⎧
⎩x⎭ = x ⋅ dx ∧ dx
>
>
>
1
определенным выше векторным полем u с координатным выражением
1
2
⎫
u 1⎧
⎩ x⎭ = x + x ,
1
2
⎫
u 2⎧
⎩ x⎭ = x − x .
>
>
>
>
>
>
Решение. Вычислим по линейности внутренней производной, подставляя координатное выражение формы q :
1
2
1
⎫ ⎧ ⎫
(u ⌟ q)⎧
⎩x⎭ = u⎩x⎭ ⌟ (x ⋅ dx ∧ dx ) =
>
=
>
>
1
⋅ x 1 ⋅ u⎧
x⎫
⌟ (dx 2 ⊗ dx 1 − dx 1 ⊗ dx 2 ) =
⎩
⎭
2
1
= ⋅ x 1 ⋅ (u⎧
x⎫
⌟ (dx 2 ⊗ dx 1 ) − u⎧
x⎫
⌟ (dx 1 ⊗ dx 2 )) =,
⎩
⎭
⎩
⎭
2
>
>
>
>
>
>
>
>
>
>
по определению внутренней производной и тензорного произведения
=
1
⎫ ⋅ dx 1 ) − (dx 1⎧u⎧x⎫⎫ ⋅ dx 2 )) =
⋅ x 1 ⋅ ((dx 2⎧
u⎧
x⎫
⎩
⎩
⎭
⎭
⎩ ⎩ ⎭⎭
2
1
1
1⎧ ⎫
2
⎫
= ⋅ x 1 ⋅ ((u 2 ⎧
⎩x⎭ ⋅ dx ) − (u ⎩x⎭ ⋅ dx )) =,
2
>
>
>
>
>
>
>
>
>
>
подставив координатное выражение векторного поля u , упростим:
=
1
⋅ x 1 ⋅ (((x 1 + x 2 ) ⋅ dx 1 ) − ((x 1 − x 2 ) ⋅ dx 2 )) =
2
1
1
= ⋅ ((x 1 )2 + x 1 ⋅ x 2 ) ⋅ dx 1 + ⋅ (x 1 ⋅ x 2 − (x 1 )2 ) ⋅ dx 2 .
2
2
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
Ответ. Итак,
1
1
2
2
1 2
1
2
1 2
1
⎫ 1
(u ⌟ q)⎧
⎩x⎭ = ⋅ ((x ) + x ⋅ x ) ⋅ dx + ⋅ (x ⋅ x − (x ) ) ⋅ dx . ⊠
>
>
>
>
>
2
§ 15
>
>
>
2
В
Задание 5. Пусть на некотором гладком многообразии заданы две дифференциальные формы
1
2
2
1
⎫
p⎧
⎩x⎭ ∶= x ⋅ dx + x ⋅ dx ,
2
1
⎫
q⎧
⎩x⎭ ∶= dx + dx ;
>
>
>
>
>
>
П Л, Ф,
46
Разбор примеров / Дифференциальные формы
вычислить их внешнее произведение.
Решение. Напомним, что внешнее произведение имеет следующие вычислительно полезные свойства:
• линейность, то есть (a ⋅ p +b ⋅ q) ∧ r = a ⋅ (p ∧ r) + b ⋅ (q ∧ r) , где a, b — числа;
• кососимметричность, то есть при перестановке двух сомножителей произведение меняет знак.
Вычислим по указанным свойствам:
1
2
2
1
1
2
⎫
(p ∧ q)⎧
⎩x⎭ = (x ⋅ dx + x ⋅ dx ) ∧ (dx + dx ) =
>
>
>
>
>
>
= − dx 1 ∧ dx 2
>
=0
>
= x ⋅ dx ∧ dx +x ⋅ dx ∧ dx 1 +
>
>
1
>
2
>
1
>
2
>
1
=0
+ x ⋅ dx ∧ dx 2 +x 2 ⋅ dx 1 ∧ dx 2 =
>
>
1
>
2
>
>
>
= (−x 1 + x 2 ) ⋅ dx 1 ∧ dx 2 .
>
>
>
>
1
2
1
2
⎫
Ответ. Итак, (p ∧ q)⎧
⎩x⎭ = (−x + x ) ⋅ dx ∧ dx . ⊠
>
Задание 6.
>
>
>
Пусть заданы две дифференциальные формы
1
2
2
1
⎫
p⎧
⎩x⎭ ∶= x ⋅ dx + x ⋅ dx ,
1
2
1
3
⎫
r⎧
⎩x⎭ ∶= dx ∧ dx + dx ∧ dx ;
>
>
>
>
>
>
>
>
вычислить внешнее произведение p ∧ r .
Решение. Вычислим по тем же свойствам:
1
2
2
1
1
2
1
3
⎫
(p ∧ r)⎧
⎩x⎭ = (x ⋅ dx + x ⋅ dx ) ∧ (dx ∧ dx + dx ∧ dx ) =
>
>
>
>
>
>
>
=0
>
=0
= x ⋅ dx ∧ dx ∧ dx +x ⋅ dx ∧ dx 1 ∧ dx 2 +
>
1
>
>
2
>
1
>
2
>
2
>
1
>
=0
+ x ⋅ dx ∧ dx ∧ dx + x ⋅ dx ∧ dx 1 ∧ dx 3 =
>
1
>
>
>
2
3
1
2
>
>
>
>
1
= −x 1 ⋅ dx 1 ∧ dx 2 ∧ dx 3 .
>
1
1
2
3
⎫
Ответ. Итак, (p ∧ r)⎧
⎩x⎭ = −x ⋅ dx ∧ dx ∧ dx . ⊠
>
Задание 7.
>
>
>
Пусть заданы две дифференциальные формы
3
1
2
1
⎫
r⎧
⎩x⎭ ∶= dx ∧ dx + dx ∧ dx ,
3
1
2
4
⎫
s⎧
⎩x⎭ ∶= dx ∧ dx + dx ∧ dx ;
>
>
>
>
>
>
>
>
вычислить внешнее произведение r ∧ s .
Н. С. Г, В. Л. Ч
>
>
>
47
Разбор примеров / Дифференциальные формы
Решение. Вычислим:
1
2
1
3
4
2
1
3
⎫
(r ∧ s)⎧
⎩x⎭ = (dx ∧ dx + dx ∧ dx ) ∧ (dx ∧ dx + dx ∧ dx ) =
>
>
>
>
>
>
>
>
= dx 1 ∧ dx 2 ∧ dx 4 ∧ dx 2 + dx 1 ∧ dx 3 ∧ dx 4 ∧ dx 2 +
>
>
>
>
>
>
>
>
+ dx 1 ∧ dx 2 ∧ dx 1 ∧ dx 3 + dx 1 ∧ dx 3 ∧ dx 1 ∧ dx 3 =
>
>
>
>
>
>
>
>
= dx 1 ∧ dx 2 ∧ dx 3 ∧ dx 4 .
>
>
>
>
1
2
3
4
⎫
Ответ. Итак, (r ∧ s)⎧
⎩x⎭ = dx ∧ dx ∧ dx ∧ dx . ⊠
>
§ 16
>
>
>
Д
Задание 8. Пусть на некотором гладком многообразии в локальных координатах задана дифференциальная форма
1
2
2
1
⎫
p⎧
⎩x⎭ ∶= x ⋅ dx + x ⋅ dx ;
>
>
>
>
вычислить дифференциал dp этой формы.
Решение. Напомним, что дифференциал линеен относительно умножения на
число, подчиняется правилу Лейбница при умножении на числовую функцию
(то есть d(f ⋅ p) = df ∧ p + f ⋅ dp ), а дифференциал внешнего произведения дифференциалов координат равен нулю.
Вычислим по указанным свойствам:
1
2
2
1
⎫
dp⎧
⎩x⎭ = d(x ⋅ dx + x ⋅ dx ) =
>
>
>
>
= − dx 1 ∧ dx 2
=0
>
=0
>
= dx ∧ dx + x ⋅ ddx + dx ∧ dx +x ⋅ ddx 1 = 0.
>
>
1
>
2
>
1
>
2
>
2
1
>
>
2
⎫
Ответ. Итак, dp⎧
⎩ x⎭ = 0 . ⊠
Задание 9.
Пусть
в локальных координатах задана дифференциальная фор-
ма
1
2
2
1 2
⎫
q⎧
⎩x⎭ ∶= (x ) ⋅ dx + x ⋅ dx ;
>
>
>
>
вычислить ее дифференциал dq .
Решение. Вычислим по тем же правилам:
1
2
2
1 2
⎫
dq⎧
⎩x⎭ = d((x ) ⋅ dx + x ⋅ dx ) =
>
>
>
>
= − dx 1 ∧ dx 2
=0
>
=0
>
= 2 ⋅ x ⋅ dx ∧ dx + (x ) ⋅ ddx + dx ∧ dx +x ⋅ ddx 1 =
>
1
>
1
>
2
>
1 2
>
2
>
2
>
1
>
2
>
= (2 ⋅ x 1 − 1) ⋅ dx 1 ∧ dx 2 .
>
П Л, Ф,
>
>
48
Разбор примеров / Производная Ли
1
1
2
⎫
Ответ. Итак, dq⎧
⎩x⎭ = (2 ⋅ x − 1) ⋅ dx ∧ dx . ⊠
>
Задание 10.
>
>
Пусть в локальных координатах задана дифференциальная фор-
ма
1
1
2
2
1
3
⎫
r⎧
⎩x⎭ ∶= x ⋅ dx ∧ dx + x ⋅ dx ∧ dx ;
>
>
>
>
>
>
вычислить ее дифференциал dr .
Решение. Вычислим:
1
1
2
2
1
3
⎫
dr⎧
⎩x⎭ = d(x ⋅ dx ∧ dx + x ⋅ dx ∧ dx ) =
>
>
>
>
>
>
=0
=0
= dx ∧ dx ∧ dx +x ⋅ d(dx ∧ dx 2 ) +
>
>
1
>
1
>
2
>
1
>
1
=0
+ dx ∧ dx ∧ dx + x ⋅ d(dx ∧ dx 3 ) =
>
>
2
>
1
>
3
>
2
1
>
= − dx 1 ∧ dx 2 ∧ dx 3 .
>
>
>
1
2
3
⎫
Ответ. Итак, dr⎧
⎩x⎭ = − dx ∧ dx ∧ dx . ⊠
>
>
>
4.2. Производная Ли
§ 17
В
Л
В этом разделе предполагается, что на некотором трехмерном многообразии
задано векторное поле j с координатным выражением
2
3
⎫
j 1⎧
⎩ x⎭ = x + x ,
1
3
⎫
j 2⎧
⎩ x⎭ = x + x ,
1
2
⎫
j 3⎧
⎩ x⎭ = x + x .
>
>
>
>
>
>
>
>
>
Задание 11. Пусть задана функция
3
2
1
⎫
f⎧
⎩ x⎭ = x ⋅ x + x ;
>
>
>
вычислить ее производную Ли полем j .
Решение. Напомним, что производная Ли гладкой функции векторным полем
есть ее производная этим полем, и вычисляется в локальных координатах она
как сумма по всем номерам координат произведений значения координаты поля
и значения частной производной этой функции.
Н. С. Г, В. Л. Ч
49
Разбор примеров / Производная Ли
Вычислим по указанному правилу:
D
⎫
⎧ ⎫ α⎧ ⎫
⎧ ⎫
(Lj f)⎧
⎩x⎭ = (j ▹ f)⎩x⎭ = j ⎩x⎭ ⋅ ∂ α f⎩x⎭ =
= (x 2 + x 3 ) ⋅ ∂ 1 (x 1 ⋅ x 2 + x 3 )+
>
>
>
>
>
>
>
>
+ (x 1 + x 3 ) ⋅ ∂ 2 (x 1 ⋅ x 2 + x 3 )+
>
>
>
>
>
>
+ (x 1 + x 2 ) ⋅ ∂ 3 (x 1 ⋅ x 2 + x 3 ) =
>
>
>
>
>
>
= (x 2 + x 3 ) ⋅ (x 2 ) + (x 1 + x 3 ) ⋅ (x 1 ) + (x 1 + x 2 ) ⋅ (1) =
>
>
>
>
>
>
>
>
= x 1 + x 2 + (x 1 )2 + (x 2 )2 + x 1 ⋅ x 3 + x 2 ⋅ x 3 .
>
>
>
>
>
>
>
>
1
2
1 2
2 2
1
3
2
3
⎫
Ответ. Итак, (Lj f)⎧
⎩x⎭ = x + x + (x ) + (x ) + x ⋅ x + x ⋅ x . ⊠
>
>
>
>
>
>
>
>
Задание 12. Пусть задано векторное поле v с координатами
2
⎫
v 1⎧
⎩ x⎭ = x ,
>
3
⎫
v 2⎧
⎩ x⎭ = x ,
>
>
1
⎫
v 3⎧
⎩ x⎭ = x ;
>
>
>
вычислить его производную Ли полем j .
Решение. Напомним, что производная Ли векторного поля другим векторным
полем есть их коммутатор (скобка Ли или скобка Пуассона); а вычисляется он
в локальных координатах по формуле
α
α⎧ ⎫
α⎧ ⎫
β⎧ ⎫
⎫ β⎧ ⎫
⟦j, v⟧ ⎧
⎩x⎭ = j ⎩x⎭ ⋅ ∂ β v ⎩x⎭ − v ⎩x⎭ ⋅ ∂ β j ⎩x⎭.
>
>
>
>
>
>
>
Вычислим первую координату:
1⎧ ⎫
α⎧ ⎫
1⎧ ⎫
1⎧ ⎫
α⎧ ⎫
⎫
(Lj v) 1⎧
⎩x⎭ = ⟦j, v⟧ ⎩x⎭ = j ⎩x⎭ ⋅ ∂ α v ⎩x⎭ − v ⎩x⎭ ⋅ ∂ α j ⎩x⎭ =
= (x 2 + x 3 ) ⋅ ∂ 1 (x 2 ) + (x 1 + x 3 ) ⋅ ∂ 2 (x 2 ) + (x 1 + x 2 ) ⋅ ∂ 3 (x 2 )−
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
− (x 2 ) ⋅ ∂ 1 (x 2 + x 3 ) − (x 3 ) ⋅ ∂ 2 (x 2 + x 3 ) − (x 1 ) ⋅ ∂ 3 (x 2 + x 3 ) =
>
>
>
>
>
>
>
>
>
>
>
>
= (x 2 + x 3 ) ⋅ 0 + (x 1 + x 3 ) ⋅ 1 + (x 1 + x 2 ) ⋅ 0−
>
>
>
>
>
>
− (x 2 ) ⋅ 0 − (x 3 ) ⋅ 1 − (x 1 ) ⋅ 1 = 0.
>
>
>
Аналогичные вычисления второй и третьей координат искомой производной
показывают, что они также нулевые.
Ответ. Итак, Lj v = 0 . ⊠
Задание 13. Пусть задана дифференциальная форма p с координатным выражением
3
2
⎫
p⎧
⎩x⎭ = x ⋅ dx ;
>
>
вычислить ее производную Ли полем j .
П Л, Ф,
50
Разбор примеров / Производная Ли
Решение. Напомним, что производная Ли дифференциальной формы p векторным полем j в локальных координатах вычисляется по формуле
β⎧ ⎫
⎫ β⎧ ⎫
⎧ ⎫
⎧ ⎫
(Lj p) α⎧
⎩x⎭ = j ⎩x⎭ ⋅ ∂ β p α ⎩x⎭ + p β ⎩x⎭ ⋅ ∂ α j ⎩x⎭.
>
>
>
>
>
>
>
⎫
Вычислим первую координату искомой производной, заметив, что p 1 ⎧
⎩ x⎭ = 0 ,
2
⎫
⎧ ⎫
p 2⎧
⎩ x⎭ = 0 , p 3 ⎩ x⎭ = x :
>
>
>
>
α⎧ ⎫
⎫ α⎧ ⎫
⎧ ⎫
⎧ ⎫
(Lj p) 1⎧
⎩ x⎭ = j ⎩ x⎭ ⋅ ∂ α p 1 ⎩ x⎭ + p α ⎩ x⎭ ⋅ ∂ 1 j ⎩ x⎭ =
1⎧ ⎫
2⎧ ⎫
3⎧ ⎫
⎫
⎧ ⎫
⎧ ⎫
= 0 + p 1⎧
⎩ x⎭ ⋅ ∂ 1 j ⎩ x⎭ + p 2 ⎩ x⎭ ⋅ ∂ 1 j ⎩ x⎭ + p 3 ⎩ x⎭ ⋅ ∂ 1 j ⎩ x⎭ =
3⎧ ⎫
2
1
2
2
⎫
= p 3⎧
⎩x⎭ ⋅ ∂ 1 j ⎩x⎭ = x ⋅ ∂ 1 (x + x ) = x .
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
Аналогичные вычисления второй и третьей координат искомой производной
2
1
3
⎫
⎧ ⎫
показывают, что (Lj p) 2⎧
⎩x⎭ = x , (Lj p) 3⎩x⎭ = x + x .
Ответ. Итак, Lj p = x 2 ⋅ dx 1 + x 2 ⋅ dx 2 + (x 1 + x 3 ) ⋅ dx 3 . ⊠
>
>
>
>
>
>
>
>
>
>
>
>
Задание 14. Пусть задана дифференциальная форма q с координатным выражением
1
2
3
⎫
q⎧
⎩x⎭ = x ⋅ dx ∧ dx ;
>
>
>
вычислить ее производную Ли полем j .
Решение. Напомним, что производная Ли подпадает под действие правила
Лейбница относительно тензорного умножения, а значит и относительно внешнего умножения и умножения на гладкую функцию; а также она перестановочна
с внешним дифференцированием форм.
Вычислим по этим свойствам:
1
2
3
⎫
(Lj q)⎧
⎩x⎭ = Lj (x ⋅ dx ∧ dx ) =,
>
>
>
по правилу Лейбница для тензорного произведения:
= (Lj x 1 ) ⋅ dx 2 ∧ dx 3 + x 1 ⋅ Lj (dx 2 ∧ dx 3 ) =
>
>
>
>
>
>
по правилу Лейбница для внешнего произведения:
= (x 2 + x 3 ) ⋅ dx 2 ∧ dx 3 + x 1 ⋅ (Lj dx 2 ) ∧ dx 3 + x 1 ⋅ dx 2 ∧ (Lj dx 3 ) =
>
>
>
>
>
>
>
>
>
>
по перестановочности внешнего дифференцирования и производной Ли:
= (x 2 + x 3 ) ⋅ dx 2 ∧ dx 3 + x 1 ⋅ d(Lj x 2 ) ∧ dx 3 + x 1 ⋅ dx 2 ∧ d(Lj x 3 ) =,
>
>
>
>
>
>
>
Н. С. Г, В. Л. Ч
>
>
>
51
Разбор примеров / Производная Ли
вычислив производные Ли, получим
= (x 2 + x 3 ) ⋅ dx 2 ∧ dx 3 + x 1 ⋅ (dx 1 + dx 3 ) ∧ dx 3 + x 1 ⋅ dx 2 ∧ (dx 1 + dx 2 ) =
>
>
>
>
>
>
>
>
>
>
>
>
по кососимметричности внешнего произведения (после раскрытия скобок):
= (x 2 + x 3 ) ⋅ dx 2 ∧ dx 3 + x 1 ⋅ dx 1 ∧ dx 3 + x 1 ⋅ dx 2 ∧ dx 1 =,
>
>
>
>
>
>
>
>
>
>
упорядочив, получим
= (x 2 + x 3 ) ⋅ dx 2 ∧ dx 3 − x 1 ⋅ dx 3 ∧ dx 1 − x 1 ⋅ dx 1 ∧ dx 2 .
>
>
>
>
>
>
>
>
>
>
Ответ. Итак,
2
3
2
3
1
3
1
1
1
2
⎫
(Lj q)⎧
⎩x⎭ = (x + x ) ⋅ dx ∧ dx − x ⋅ dx ∧ dx − x ⋅ dx ∧ dx . ⊠
>
§ 18
>
>
>
И
>
>
>
>
>
>
С
Задание 15. Пусть на некотором двумерном гладком многообразии в локальных координатах задана дифференциальная форма
1 2
2
2
1
⎫
q⎧
⎩x⎭ ∶= (x ) ⋅ dx + x ⋅ dx ,
>
>
>
>
и векторные поля
1
2⎧ ⎫
1
2
⎫
u 1⎧
⎩x⎭ ∶= x , u ⎩x⎭ ∶= x + x ,
2
2⎧ ⎫
1
2
⎫
v 1⎧
⎩x⎭ ∶= x , v ⎩x⎭ ∶= x + x ;
вычислить значение dq ◂(u, v) формы dq на векторных полях u и v непосредственно и по инфинитезимальной формуле Стокса, сравнив после результаты.
>
>
>
>
>
>
>
>
>
>
Решение. Вычислим вначале непосредственно, воспользовашись вычисленным
1
1
2
⎫
дифференциалом этой формы ( dq⎧
⎩x⎭ = (2 ⋅ x − 1) ⋅ dx ∧ dx , см. Задание 9):
>
>
>
2 ⎧ ⎧ ⎫ ⎧ ⎫⎫
1
1
⎫
(dq ◂(u, v))⎧
⎩x⎭ = ((2 ⋅ x − 1) ⋅ dx ∧ dx )⎩u⎩x⎭, v⎩x⎭⎭ =
1
⎧ ⎫ ⎧ ⎫⎫
= ⋅ (2 ⋅ x 1 − 1) ⋅ (dx 1 ⊗ dx 2 − dx 2 ⊗ dx 1 )⎧
⎩u⎩x⎭, v⎩x⎭⎭ =
2
>
>
>
>
>
=
>
>
>
1
2⎧ ⎧ ⎫⎫
2⎧ ⎧ ⎫⎫
1⎧ ⎧ ⎫⎫
⎧ ⎫⎫
⋅ (2 ⋅ x 1 − 1) ⋅ (dx 1⎧
⎩u⎩x⎭⎭ ⋅ dx ⎩v⎩x⎭⎭ − dx ⎩u⎩x⎭⎭ ⋅ dx ⎩v⎩x⎭⎭) =
2
1
= ⋅ (2 ⋅ x 1 − 1) ⋅ (u 1 ⎧
x⎫
⋅ v 2⎧
x⎫
− u 2⎧
x⎫
⋅ v 1⎧
x⎫
⎩
⎭
⎩
⎭
⎩
⎭
⎩
⎭) =
2
1
= ⋅ (2 ⋅ x 1 − 1) ⋅ (x 1 ⋅ (x 1 + x 2 ) − (x 1 + x 2 ) ⋅ x 2 ) =
2
1
= ⋅ (2 ⋅ x 1 − 1) ⋅ ((x 1 )2 − (x 2 )2 ).
2
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
П Л, Ф,
>
52
Разбор примеров / Производная Ли
Теперь же вычислим значение q ◂ v формы q на векторном поле v :
1 2
2
2
1 ⎧ ⎧ ⎫⎫
⎫
(q ◂ v)⎧
⎩x⎭ = ((x ) ⋅ dx + x ⋅ dx )⎩v⎩x⎭⎭ =
2
1⎧ ⎧ ⎫⎫
⎧ ⎫⎫
= (x 1 )2 ⋅ dx 2⎧
⎩v⎩x⎭⎭ + x ⋅ dx ⎩v⎩x⎭⎭ =
2
1⎧ ⎫
⎫
= (x 1 )2 ⋅ v 2 ⎧
⎩ x⎭ + x ⋅ v ⎩ x⎭ =
>
>
>
>
>
>
>
>
>
>
>
>
= (x 1 )2 ⋅ (x 1 + x 2 ) + x 2 ⋅ x 2 ;
>
>
>
>
>
D
из чего вычислим производную u ▹(q ◂ v) полученной функции полем u :
D
1⎧ ⎫
2⎧ ⎫
⎫
⎧ ⎫
⎧ ⎫
u ▹(dq ◂ v)⎧
⎩x⎭ = u ⎩x⎭ ⋅ ∂ 1 (q ◂ v)⎩x⎭ + u ⎩x⎭ ⋅ ∂ 2 (q ◂ v)⎩x⎭ =
= x 1 ⋅ ∂ 1 ((x 1 )3 + (x 1 )2 ⋅ x 2 + (x 2 )2 )+
>
>
>
>
>
>
>
>
>
>
+ (x 1 + x 2 ) ⋅ ∂ 2 ((x 1 )3 + (x 1 )2 ⋅ x 2 + (x 2 )2 ) =
>
>
>
>
>
>
>
= x 1 ⋅ (3 ⋅ (x 1 )2 + 2 ⋅ x 1 ⋅ x 2 ) + (x 1 + x 2 ) ⋅ ((x 1 )2 + 2 ⋅ x 2 ) =
>
>
>
>
>
>
>
>
= 2 ⋅ x 1 ⋅ x 2 + 2 ⋅ (x 2 )2 + 4 ⋅ (x 1 )3 + 3 ⋅ (x 1 )2 ⋅ x 2 .
>
>
>
>
>
>
Затем вычислим q ◂ u :
1 2
2
2
1 ⎧ ⎧ ⎫⎫
⎫
(q ◂ u)⎧
⎩x⎭ = ((x ) ⋅ dx + x ⋅ dx )⎩u⎩x⎭⎭ =
2
1⎧ ⎧ ⎫⎫
⎧ ⎫⎫
= (x 1 )2 ⋅ dx 2⎧
⎩u⎩x⎭⎭ + x ⋅ dx ⎩u⎩x⎭⎭ =
2
1⎧ ⎫
⎫
= (x 1 )2 ⋅ u 2 ⎧
⎩ x⎭ + x ⋅ u ⎩ x⎭ =
>
>
>
>
>
>
>
>
>
>
>
>
= (x 1 )3 + (x 1 )2 ⋅ x 2 + x 1 ⋅ x 2 ;
>
>
>
>
>
из чего вычислим d(q ◂ u) :
1 3
1 2
2
1
2
⎫
d(q ◂ u)⎧
⎩x⎭ = d((x ) + (x ) ⋅ x + x ⋅ x ) =
>
>
>
>
>
= 3 ⋅ (x 1 )2 ⋅ dx 1 + x 1 ⋅ dx 2 + x 2 ⋅ dx 1 + 2 ⋅ x 1 ⋅ x 2 ⋅ dx 1 + (x 1 )2 ⋅ dx 2 ;
>
>
>
>
>
>
>
>
>
>
>
и отсюда вычислим d(q ◂ u) ◂ v :
2
1
1
1 2
⎫
(d(q ◂ u) ◂ v)⎧
⎩x⎭ = (3 ⋅ (x ) ⋅ dx + x ⋅ dx +
>
>
>
>
⎧ ⎫⎫
+ x 2 ⋅ dx 1 + 2 ⋅ x 1 ⋅ x 2 ⋅ dx 1 + (x 1 )2 ⋅ dx 2 )⎧
⎩v⎩x⎭⎭ =
= (x 1 )2 + x 1 ⋅ x 2 + (x 2 )2 + (x 1 )3 + 4 ⋅ (x 1 )2 ⋅ x 2 + 2 ⋅ x 1 ⋅ (x 2 )2 .
>
>
>
>
>
>
>
>
>
>
>
>
>
>
Далее нетрудно установить, что
1
1
⎫
⟦u, v⟧ ⎧
⎩ x⎭ = x ,
>
>
2
2
1
⎫
⟦u, v⟧ ⎧
⎩ x⎭ = x − x ;
>
Н. С. Г, В. Л. Ч
>
>
>
>
53
Разбор примеров / Теорема Фробениуса
из чего следует
1 3
1 2
2
1
2
⎫
(q ◂ ⟦u, v⟧)⎧
⎩x⎭ = (x ) − (x ) ⋅ x + x ⋅ x .
>
>
>
>
>
Ответ. Итак, сложив полученные выражения по формуле:
D
u ▹(q ◂ v) − d(q ◂ u) ◂ v − q ◂ ⟦u, v⟧ ,
получим 2 ⋅ dq ◂(u, v) . ⊠
4.3. Теорема Фробениуса
§ 19
О
Задание 16. Пусть в трехмерном многообразии на окрестности его точки y
с координатами y 1 = y 2 = y 3 = 0 задано распределение с базисом из одного
векторного поля v1 , координатное выражение которого есть
>
>
>
2
⎫
v12 ⎧
⎩ x⎭ = x ,
1
⎫
v11 ⎧
⎩ x⎭ = x ,
>
>
>
>
3
⎫
v13 ⎧
⎩x⎭ = x + 1;
>
>
используя метод доказательства Теоремы Фробениуса к заданному распределению построить функции из определения вполне интегрируемости.
Решение. Заметив, что коммутатор векторного поля v1 с ним самим есть нуль,
заключим по Лемме 14, что распределение инволютивно; поэтому искомые
функции существуют.
Дополним систему {v1 } до размерности 3 векторными полями v2 и v3 с
координатными выражениями
⎫
v22 ⎧
⎩x⎭ = 0,
⎫
v32 ⎧
⎩x⎭ = 1,
⎫
v21 ⎧
⎩x⎭ = 1,
⎫
v31 ⎧
⎩x⎭ = 0,
>
>
>
>
⎫
v23 ⎧
⎩x⎭ = 0;
⎫
v33 ⎧
⎩x⎭ = 0;
>
>
и заметим, что в окрестности точки y эти три поля линейно независимы.
Решив для этих полей определяющие уравнения (1), запишем координатные
выражения их потоков k1 , k2 , k3 :
⎛
x 1 ⋅ et
⎫ ⎜
k1 ⎧
x 2 ⋅ et
⎩t, x⎭ ∶ ⎜
⎜
⎝ (x 3 + 1) ⋅ et − 1
>
>
>
⎛ t+x
⎫ ⎜ x2
k2 ⎧
⎩t, x⎭ ∶ ⎜
⎜
⎝ x3
>
>
>
1
⎞
⎟
⎟,
⎟
⎠
⎞
⎟
⎟,
⎟
⎠
⎛ x1
⎫ ⎜ t+x
k3 ⎧
⎩t, x⎭ ∶ ⎜
⎜
⎝ x3
>
>
>
2
⎞
⎟
⎟.
⎟
⎠
П Л, Ф,
54
Разбор примеров / Теорема Фробениуса
Для начальной точки y и параметров t1 , t2 , t3 Ð→ 0 построим отображение
1 2 3⎫
⎧ t1 , ⋅ ⎫
⎧ t2 , ⋅ ⎫
⎧ t3 , ⋅ ⎫
⎧ ⎫
m⎧
⎪
⎩t , t , t ⎪
⎭ = k1 ⎪
⎩ ⎪
⎭ ○ k2 ⎪
⎩ ⎪
⎭ ○ k3 ⎪
⎩ ⎪
⎭⎩y⎭ (то есть по формуле Леммы 11)
с координатным выражением
⎞
⎟
⎟;
⎟
⎠
⎛ t2 ⋅ e t
1 2 3⎫ ⎜ 3
t1
m⎧
⎪
⎭∶ ⎜
⎩t , t , t ⎪
⎜ t 1⋅ e
⎝ et − 1
1
1 2 3⎫
и выразим зависимость параметров t1 , t2 , t3 Ð→ 0 от значений m⎧
⎪
⎩t , t , t ⎪
⎭= x
отображения m :
1⎧
x
t = g ⎩ x⎫
=
⎭ 1 + x 3.
x
t = g ⎩ x⎫
=
⎭ 1 + x 3,
1⎫
⎧
t = g ⎩ x⎫
⎭ = ln⎩1 + x ⎭,
1
>
1
2⎧
2
>
>
>
2
3⎧
3
>
Проверим, что дифференциал dg2 обнулится на поле v1 :
⎫
dg2 ⎧
⎩ x⎭ =
1
(1 + x
⋅ ((1 + x 3 ) ⋅ dx 1 − x 1 ⋅ dx 3 ), следовательно
>
3 )2
>
⎫⎧ ⎧ ⎫⎫
dg2 ⎧
⎩x⎭⎩v1 ⎩x⎭⎭ =
>
1
>
>
1
3⎧ ⎫
⎫
⋅ ((1 + x 3 ) ⋅ v11 ⎧
⎩x⎭ − x ⋅ v1 ⎩x⎭) =
(1 + x 3 )2
1
=
⋅ ((1 + x 3 ) ⋅ x 1 − x 1 ⋅ (x 3 + 1)) = 0,
(1 + x 3 )2
>
>
>
>
>
>
>
>
>
>
а дифференциал dg3 ведет себя так же.
Наконец заметим, что дифференциалы dg2 и dg3 линейно независимы, ибо
различаются номера координат, дифференциалы которых участвуют в них; заключим из этого, что функция g3 соответствует условиям Задания.
Ответ. В качестве искомых функций могут быть избраны построенные функции
x
g ⎩ x⎫
⎭= 1 + x 3 ,
>
1
2⎧
§ 20
>
x
g ⎩ x⎫
⎭= 1 + x 3 . ⊠
>
2
3⎧
>
Д
Задание 17. Пусть в трехмерном многообразии на окрестности его точки
y с координатами y 1 = y 2 = y 3 = 0 задано распределение с базисом из двух
векторных полей v1 и v2 , координатное выражение которых есть
>
>
>
⎛ 2⋅x 3−2
⎜
v1 ∶ ⎜
−1
⎜
⎝
0
>
⎞
⎟
⎟,
⎟
⎠
⎛ −x 1
⎜
v2 ∶ ⎜ − 2 ⋅ x 2
⎜
⎝ x 3−1
>
>
>
Н. С. Г, В. Л. Ч
⎞
⎟
⎟;
⎟
⎠
55
Разбор примеров / Теорема Фробениуса
используя метод доказательства Теоремы Фробениуса к заданному распределению построить функцию из определения вполне интегрируемости.
Решение. Установим инволютивность распределения, вычислив коммутатор поβ
β
α
лей его базиса (матрично запишем формулу ⟦v1 , v2 ⟧ = v1 ⋅ ∂ β v2α − v2 ⋅ ∂ β v1α ):
>
>
>
>
>
>
⎛ ⟦v1 , v2 ⟧
⎜
⎜ ⟦v1 , v2 ⟧
⎜
⎝ ⟦v1 , v2 ⟧
>
1
⎞
⎛ ∂ 1 v21 ∂ 2 v21 ∂ 3 v21
⎟⎧ ⎫ ⎜
⎟⎩x⎭ = ⎜ ∂ 1 v22 ∂ 2 v22 ∂ 3 v22
⎟
⎜
⎠
⎝ ∂ 1 v23 ∂ 2 v23 ∂ 3 v23
>
>
>
>
2
>
3
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
⎞
⎛ v11
⎟⎧ ⎫ ⎜ 2
⎟ ⎩ x⎭ ⋅ ⎜ v 1
⎟
⎜
⎠
⎝ v13
>
>
>
⎞
⎟⎧ ⎫
⎟⎩x⎭−
⎟
⎠
⎛ ∂ 1 v11 ∂ 2 v11 ∂ 3 v11
⎜
− ⎜ ∂ 1 v12 ∂ 2 v12 ∂ 3 v12
⎜
⎝ ∂ 1 v13 ∂ 2 v13 ∂ 3 v13
>
>
>
>
>
>
>
⎞ ⎛0 0 2
⎟ ⎜
⎟−⎜ 0 0 0
⎟ ⎜
⎠ ⎝0 0 0
⎛ −2 ⋅ x 3 + 2
⎜
=⎜
2
⎜
⎝
0
>
>
>
>
>
>
>
>
⎛ −1 0 0 ⎞ ⎛ 2 ⋅ x 3 − 2
⎟ ⎜
⎜
= ⎜ 0 −2 0 ⎟ ⋅ ⎜
−1
⎟ ⎜
⎜
⎝ 0 0 1⎠ ⎝
0
>
>
>
>
>
>
⎞ ⎛ −x 1
⎟ ⎜
⎟ ⋅ ⎜ −2 ⋅ x 2
⎟ ⎜
⎠ ⎝ x 3−1
>
>
>
>
>
>
⎞
⎟⎧ ⎫
⎟ ⎩ x⎭ =
⎟
⎠
⎞
⎟
⎟=
⎟
⎠
⎞ ⎛ 2⋅x 3−2
⎟ ⎜
⎟−⎜
0
⎟ ⎜
⎠ ⎝
0
>
⎞
⎛ v21
⎟⎧ ⎫ ⎜ 2
⎟ ⎩ x⎭ ⋅ ⎜ v 2
⎟
⎜
⎠
⎝ v23
⎞ ⎛ −4 ⋅ x 3 + 4
⎟ ⎜
⎟=⎜
2
⎟ ⎜
⎠ ⎝
0
>
⎞
⎟
⎟;
⎟
⎠
ясно, что ⟦v1 , v2 ⟧ = −2 ⋅ v1 ; тем самым распределение инволютивно.
Дополним систему {v1 , v2 } векторным полем v3 с координатным выражением
⎛0⎞
⎜ ⎟
⎜ 1 ⎟;
⎜ ⎟
⎝0⎠
и заметим, что в окрестности точки y эти три поля линейно независимы.
Решив для этих полей определяющие уравнения (1), запишем координатные
выражения их потоков k1 , k2 , k3 :
⎛ 2 ⋅ (x 3 − 1) ⋅ t + x
⎫ ⎜
k1 ⎧
−t + x 2
⎩t, x⎭ ∶ ⎜
⎜
⎝
x3
>
>
>
⎛
x 1 ⋅ e−t
⎫ ⎜
k2 ⎧
x 2 ⋅ e−2⋅t
⎩t, x⎭ ∶ ⎜
⎜
⎝ (x 3 − 1) ⋅ et + 1
>
>
>
⎞
⎟
⎟,
⎟
⎠
>
1
⎞
⎟
⎟,
⎟
⎠
⎛ x1
⎫ ⎜ t+x
k3 ⎧
⎩t, x⎭ ∶ ⎜
⎜
⎝ x3
>
>
>
2
⎞
⎟
⎟.
⎟
⎠
Для начальной точки y и параметров t1 , t2 , t3 Ð→ 0 по формуле Леммы 11
П Л, Ф,
56
Разбор примеров / Теорема Фробениуса
построим отображение m с координатным выражением
⎛ − 2 ⋅ t1 ⋅ e t
1 2 3⎫ ⎜
1
3
−2⋅t2
m⎧
⎪
−t
+
t
⋅
e
⎩t , t , t ⎪
⎭∶ ⎜
⎜
2
⎝
1 − et
2
⎞
⎟
⎟;
⎟
⎠
1 2 3⎫
и выразим зависимость параметров t1 , t2 , t3 Ð→ 0 от значений m⎧
⎪
⎭= x
⎩t , t , t ⎪
отображения m :
x1
t = g ⎩ x⎫
=
⎭ 2 ⋅ (x 3 − 1) ,
>
1⎧
1
>
3
⎫
t2 = g2 ⎧
⎩x⎭ = ln(1 − x ),
>
1
2
3
2
1
3
⎫
t3 = g3 ⎧
⎩x⎭ = x ⋅ (x − 1) + ⋅ x ⋅ (x − 1).
>
>
>
>
2
Запишем дифференциал dg3 :
3
1
3
2
2
⎫ 1
dg3 ⎧
⎩x⎭ = ⋅ (x − 1) ⋅ dx + (x − 1) ⋅ dx +
>
2
>
>
+ (2 ⋅ (x 3 − 1) ⋅ x 2 +
>
>
>
1
⋅ x 1 ) ⋅ dx 3 .
2
>
>
Вычислим значение этого дифференциала на поле v1 :
3
3
3
2
⎫⎧ ⎧ ⎫⎫ 1
dg3 ⎧
⎩x⎭⎩v1 ⎩x⎭⎭ = ⋅ (x − 1) ⋅ (2 ⋅ x − 2) + (x − 1) ⋅ (−1)+
>
>
>
2
+ (2 ⋅ (x 3 − 1) ⋅ x 2 +
>
>
1
⋅ x 1 ) ⋅ 0 = 0;
2
>
и аналогично на поле v2 .
3
⎫
Из неравенства dg3 ⎧
⎩y⎭ ≠ 0 следует, что функция g соответствует условиям
Задания.
Ответ. В качестве искомой функции может быть избрана построенная функция
1
1
3
2
3
2
⎫
g3 ⎧
⎩x⎭ = x ⋅ (x − 1) + ⋅ x ⋅ (x − 1). ⊠
>
>
>
2
Н. С. Г, В. Л. Ч
>
Задачи для самостоятельного решения / Дифференциальные формы
57
5. Задачи для самостоятельного решения
5.1. Дифференциальные формы
§ 21
В
Задание 18. Пусть на некотором двумерном многообразии задана дифференциальная форма p валентности 1 , выраженная в локальных координатах по
формуле
2 2
2
2
1
⎫
p⎧
⎩x⎭ = (x ) ⋅ dx − ⋅x ⋅ dx ,
>
>
>
>
а в точке y с координатами y 1 = 4 и y 2 = −4 задан вектор v с координатами
⎫⎧ ⎫
v 1 = −10 и v 2 = 1 ; вычислить значение p⎧
⎩y⎭⎩v⎭ дифференциальной формы p
в точке y на касательном векторе v в той же точке.
>
>
>
>
Задание 19. Пусть на некотором двумерном многообразии задана дифференциальная форма p валентности 1 , выраженная в локальных координатах по
формуле
2
2
1
1
⎫
p⎧
⎩x⎭ = x ⋅ dx − ⋅x ⋅ dx ,
>
>
>
>
а также задано векторное поле u с координатным выражением
1
2
⎫
u 1⎧
⎩ x⎭ = x + 5 ⋅ x ,
1
2
⎫
u 2⎧
⎩ x⎭ = 5 ⋅ x − x ;
>
>
>
>
>
>
вычислить координатное выражение гладкой функции p ◂ u — значения формы
p на векторном поле u .
Задание 20. Пусть теперь задана дифференциальная форма q валентности
2 с координатным выражением
2
2
1
⎫
q⎧
⎩x⎭ = x ⋅ dx ∧ dx ,
>
>
>
и в точке y с координатами y 1 = −1 и y 2 = 1 заданы вектор v с координатами
v 1 = 1 , v 2 = 1 и вектор w с координатами w 1 = 1 , w 2 = 1 ; вычислить значение
⎫⎧
⎫
q⎧
⎩y⎭⎩v, w⎭ формы q в точке y на векторах v, w .
>
>
>
>
>
>
Задание 21. Вычислить значение u ⌟ q внутренней производной формы q
валентности 2 с координатным выражением
2
2
⎫
q⎧
⎩x⎭ = x ⋅ dx ∧ dx
>
>
>
1
определенным выше векторным полем u с координатным выражением
2
1
⎫
u 1⎧
⎩ x⎭ = 5 ⋅ x + x ,
2
1
⎫
u 2⎧
⎩ x⎭ = x − 5 ⋅ x .
>
>
>
>
>
>
П Л, Ф,
58
§ 22
Задачи для самостоятельного решения / Производная Ли
В
Задание 22. Пусть на некотором гладком многообразии заданы две дифференциальные формы
2
1
1
⎫
p⎧
⎩x⎭ ∶= dx + x ⋅ dx ,
1
1
2
⎫
q⎧
⎩x⎭ ∶= x ⋅ dx + dx ;
>
>
>
>
>
>
вычислить их внешнее произведение.
Задание 23.
Пусть заданы две дифференциальные формы
2
1
⎫
p⎧
⎩x⎭ ∶= dx + dx ,
3
1
2
2
1
3
⎫
r⎧
⎩x⎭ ∶= x ⋅ dx ∧ dx + x ⋅ dx ∧ dx ;
>
>
>
>
>
>
>
>
вычислить внешнее произведение p ∧ r .
Задание 24.
Пусть заданы две дифференциальные формы
1
2
2
3
⎫
r⎧
⎩x⎭ ∶= dx ∧ dx + dx ∧ dx ,
3
2
4
1
⎫
s⎧
⎩x⎭ ∶= dx ∧ dx + dx ∧ dx ;
>
>
>
>
>
>
>
>
вычислить внешнее произведение r ∧ s .
§ 23
Д
Задание 25. Пусть на некотором гладком многообразии в локальных координатах задана дифференциальная форма
2
2
2
1
⎫
p⎧
⎩x⎭ ∶= x ⋅ dx − x ⋅ dx ;
>
>
>
>
вычислить дифференциал dp этой формы.
Задание 26.
Пусть в локальных координатах задана дифференциальная фор-
ма
1
2 2
2
1 2
⎫
q⎧
⎩x⎭ ∶= (x ) ⋅ dx + (x ) ⋅ dx ;
>
>
>
>
вычислить ее дифференциал dq .
Задание 27.
Пусть в локальных координатах задана дифференциальная фор-
ма
3
1
3
2
1
2
⎫
r⎧
⎩x⎭ ∶= x ⋅ dx ∧ dx + x ⋅ dx ∧ dx ;
>
>
>
>
вычислить ее дифференциал dr .
Н. С. Г, В. Л. Ч
>
>
59
Задачи для самостоятельного решения / Производная Ли
5.2. Производная Ли
§ 24
В
Л
В этом разделе предполагается, что на некотором трехмерном многообразии
задано векторное поле j с координатным выражением
2
3
⎫
j 1⎧
⎩ x⎭ = x + x ,
1
3
⎫
j 2⎧
⎩ x⎭ = x + x ,
1
2
⎫
j 3⎧
⎩ x⎭ = x + x .
>
>
>
>
>
>
>
>
>
Задание 28. Пусть задана функция
2
1
3
⎫
f⎧
⎩ x⎭ = x ⋅ x + x ;
>
>
>
вычислить ее производную Ли полем j .
Задание 29. Пусть задано векторное поле v с координатами
2
⎫
v 1⎧
⎩ x⎭ = 2 ⋅ x ,
>
>
3
⎫
v 2⎧
⎩ x⎭ = 3 ⋅ x ,
>
1
⎫
v 3⎧
⎩ x⎭ = 4 ⋅ x ;
>
>
>
вычислить его производную Ли полем j .
Задание 30. Пусть задана дифференциальная форма p с координатным выражением
1
3
⎫
p⎧
⎩x⎭ = x ⋅ dx ;
>
>
вычислить ее производную Ли полем j .
Задание 31. Пусть задана дифференциальная форма q с координатным выражением
3
1
2
⎫
q⎧
⎩x⎭ = x ⋅ dx ∧ dx ;
>
>
>
вычислить ее производную Ли полем j .
§ 25
И
С
Задание 32. Пусть на некотором двумерном гладком многообразии в локальных координатах задана дифференциальная форма
2
2
1
1
⎫
q⎧
⎩x⎭ ∶= x ⋅ dx − x ⋅ dx ,
>
>
и векторные поля
2
⎫
u 1⎧
⎩x⎭ ∶= x ,
1
⎫
v 1⎧
⎩x⎭ ∶= x ,
>
>
>
>
>
>
2
1
⎫
u 2⎧
⎩x⎭ ∶= x − x ,
2
1
⎫
v 2⎧
⎩x⎭ ∶= x − x ;
>
>
>
>
>
>
П Л, Ф,
60
Задачи для самостоятельного решения / Теория Фробениуса
вычислить значение dq ◂(u, v) формы dq на векторных полях u и v непосредственно и по инфинитезимальной формуле Стокса, сравнив после результаты.
5.3. Теория Фробениуса
§ 26
О
Задание 33. Пусть в трехмерном многообразии на окрестности его точки y
с координатами y 1 = y 2 = y 3 = 0 задано распределение с базисом из одного
векторного поля v1 , координатное выражение которого есть
>
>
>
1
⎫
⎛ v11 ⎧
⎩ x⎭ ⎞ ⎛ x
⎜ 2⎧ ⎫ ⎟ ⎜
⎜ v 1 ⎩ x⎭ ⎟ = ⎜ x 2
⎜
⎟ ⎜
⎫⎠ ⎝ x 3+2
⎝ v13 ⎧
x
⎩ ⎭
>
>
>
>
>
>
⎞
⎟
⎟;
⎟
⎠
используя метод доказательства Теоремы Фробениуса к заданному распределению построить функции из определения вполне интегрируемости.
§ 27
Д
Задание 34. Пусть в трехмерном многообразии на окрестности его точки
y с координатами y 1 = y 2 = y 3 = 0 задано распределение с базисом из двух
векторных полей v1 и v2 , координатное выражение которых есть
>
>
>
⎛ x 3−1
⎜
v1 ∶ ⎜ −1/2
⎜
⎝ 0
>
⎞
⎟
⎟,
⎟
⎠
⎛ −x 1
⎜
v2 ∶ ⎜ − 2 ⋅ x 2
⎜
⎝ x 3−1
>
>
>
⎞
⎟
⎟;
⎟
⎠
используя метод доказательства Теоремы Фробениуса к заданному распределению построить функцию из определения вполне интегрируемости.
Н. С. Г, В. Л. Ч
Список обозначений
Везде применяется тензорное правило Эйнштейна:
если в некоторой формуле есть произведение величин с верхними и нижними индексами, и какой-то
индекс встречается в этом произведении только однажды как верхний и как нижний, то в формуле по этому
индексу производится суммирование слагаемых вида этого произведения, причем диапазон изменения этого
индекса в сумме следует из контекста формулы.
Переменные
вид формулы — обозначаемое
α, β, γ, . . .
— числа нумерации объектов или координат.
τ
— перестановка на некотором множестве {1, . . . , α} .
a, b, t
— вещественные числа (параметры).
f, g, h, k
— параметризованное число, отображение.
x, y
— точки многообразия.
M, N
— многообразия.
D, U
— открытые подмножества многообразия.
c
— карта на многообразии.
k
— поток векторного поля.
m
— параметризованная точка многообразия, отображение.
u, v, w
— вектор, касательный вектор.
j, u, v, w
— вектор параметризованный, векторное поле.
p, q, r
— кокасательный тензор, ковариантный тензор.
p, q, r, s
— ковариантное тензорное поле, дифференциальная форма.
Z
— распределение (касательных подпространств).
Специальные обозначения
вид формулы — обозначаемое
R
— множество всех вещественных чисел.
im f
— образ (совокупность всех значений) отображения f .
c
−1
— обратное отображение к инъективному c .
kronαβ
— символ (функция) Кронекера: kronαβ = {
sign τ
— знак перестановки τ .
alt p
— альтернация ковариантного тензора p .
x
v
α
— координата с номером α точки x .
α
— координата с номером α вектора v .
>
>
p
α,...,β
>
1
0
при α = β ,
при α ≠ β .
— координата с номерами α, . . . , β ковариантного тензора p .
C∞ (M)
— линейная алгебра гладких функций на многообразии M .
Tx M
— касательное пространство в точке x ко многообразию M .
T
∗
xM
tpr v
— кокасательное пространство в точке x ко многообразию M .
— проекция касательного вектора v в точку, к которой является касательным
пространство этого вектора.
61
tpr p
— проекция ковариантного тензора p в точку, к которой является касательным
пространство этого тензора.
∂α f
∂ αf
∂0 k
∂ αm
— частная производная числового отображения f по аргументу с номером α .
df
— дифференциал гладкой функции f .
dm
— дифференциал отображения m .
dp
— дифференциал дифференциальной формы p .
>
>
— производная гладкой функции f по координате с номером α .
— производная потока k по параметру траектории.
— производная отображения m по координате с номером α .
Операции
вид формулы — обозначаемое
τ↪p
— действие перестановки τ на ковариантном тензоре p .
p⊗q
— тензорное произведение ковариантных тензоров p и q .
u∧v
— внешнее произведение векторов u и v .
p∧q
— внешнее произведение ковариантных тензоров p и q .
D
v▹f
— производная векторным полем v гладкого числового отображения f .
⟦u, v⟧
— коммутатор векторных полей u и v .
Lj f
Lj v
Lj p
— производная Ли векторного поля v векторным полем j .
— производная Ли ковариантного тензорного поля p векторным полем j .
v⌟p
— внутренняя производная вектором v ковариантного тензора p .
α
— производная Ли гладкой функции f векторным полем j .
p←
Ðv
— подстановка вектора v как α-того аргумента ковариантного тензора p .
p ◂ v1 , . . . , vα
— функциональное значение ковариантного тензорного поля p валентности α
на векторных полях v1 , . . . , vα .
m↶p
— перенос ковариантного тензора p против отображения m в точку x .
m↶p
— перенос ковариантного тензорного поля p против отображения m .
jÀf
— перенос функции f потоком векторного поля j .
jÀv
— перенос векторного поля v потоком векторного поля j .
jÀp
— перенос ковариантного тензорного поля p потоком векторного поля j .
x
⋆
62
Предметный указатель
атлас (многообразия), 9
атлас гладкий (многообразия), 9
базис касательный канонический, 10
вектор касательный, 10
вектор касательный ко кривой, 10
вектор кокасательный, 11
вектора координаты локальные, 10
векторного поля перенос векторным полем,
22
векторного поля производная Ли, 24
гладкого отображения дифференциал, 13
гладкой функции дифференциал, 13
гладкой функции перенос векторным полем, 22
гладкой функции производная Ли, 23
дифференциал внешний, 17
дифференцирование функции векторным
полем, 11
знак перестановки, 6
инверсия в перестановке, 6
инфинитезимальная формула Стокса, 31
карт согласованность гладкая, 9
карт согласованность непрерывная, 8
карта (многообразия), 8
касательное пространство, 10
ковариантного тензора внутренняя производная, 7
ковариантного тензорного поля перенос
векторным полем, 22
ковариантного тензорного поля производная Ли, 24
коммутатор, 11
координатное ковекторное поле, 12
координаты локальные, 8
кривая гладкая, 9
многообразие, 9
многообразие гладкое, 9
отображение многообразий гладкое, 9
перестановка, 6
поле векторное, 10
поле касательное координатное, 11
поле тензорное ковариантное, 12
поля векторного поток, 14
проекция вектора, 10
проекция тензора, 11
производная по координате, 10
тензор ковариантный кососимметричный, 6
тензора ковариантного альтернация, 6
тензоров кососимметричных произведение
внешнее, 7
тензоров произведение тензорное, 6
формула Картана, 19
функция гладкая, 9
распределение, 37
распределение вполне интегрируемое, 37
распределение инволютивное, 37
распределения локальный базис, 37
распределения сечение, 37
скобка Ли, 11
скобка Пуассона, 11
тензор ковариантный антисимметричный, 6
тензор ковариантный в точке, 11
63
Список литературы
[1] Краснощёченко В. И., Крищенко А. П. Нелинейные системы: геометрические
методы анализа и синтеза. — М. : Издательство МГТУ имени Н. Э.
Баумана, 2005. — 520 с.
[2] Арнольд В. И. Математические методы классической механики. — М. :
Наука, 1979. — 432 с.
[3] Isidori A. Nonlinear control systems. — London : Springer-Verlag, 1995. — xv +
549 с.
[4] Канатников А. Н., Крищенко А. П., Четвериков В. Н. Дифференциальное
исчисление функций многих переменных. — М. : Издательство МГТУ имени
Н. Э. Баумана, 2000. — 456 с. — (Серия «Математика в техническом
университете», выпуск V).
[5] Иванов А. О., Тужилин А. А. Лекции по классической дифференциальной
геометрии. — М. : Университетская книга; Логос, 2009. — 224 с.
[6] Рашевский П. К. Курс дифференциальной геометрии. — М. : Эдиториал
УРСС, 2003. — 429 с.
[7] Мищенко А. С., Фоменко А. Т. Курс дифференциальной геометрии и
топологии. — М. : Издательство «Факториал Пресс», 2000. — 448 с.
[8] Дубровин Б. А., Новиков С. П., Фоменко А. Т. Современная геометрия. В
3-х т. Т. 1. Геометрия поверхностей, групп преобразований и полей. — М.
: Эдиториал УРСС, 1998. — 336 с.
[9] Дубровин Б. А., Новиков С. П., Фоменко А. Т. Современная геометрия. В
3-х т. Т. 2. Геометрия и топология многообразий. — М. : Эдиториал УРСС,
1998. — 280 с.
[10] Хорькова Н. Г., Чередниченко А. В. Элементы дифференциальной геометрии
и топологии. Кривые в пространстве. — М. : Издательство МГТУ имени
Н. Э. Баумана, 2007. — 48 с.
[11] Хорькова Н. Г. Элементы дифференциальной геометрии и топологии. Риманова геометрия и тензорный анализ. — М. : Издательство МГТУ имени
Н. Э. Баумана, 2005. — 84 с.
64
[12] Рашевский П. К. Риманова геометрия и тензорный анализ. — М. : Эдиториал УРСС, 2003. — 664 с.
[13] Хорькова Н. Г., Четвериков В. Н. Элементы дифференциальной геометрии
и топологии. Векторные поля на многообразиях. Учебное пособие. — М. :
Издательство МГТУ имени Н. Э. Баумана, 1996. — 48 с.
[14] Мищенко А. С., Соловьев Ю. П., Фоменко А. Т. Сборник задач по
дифференциальной геометрии и топологии. — М. : Издательство физикоматематической литературы, 2001. — 351 с.
65