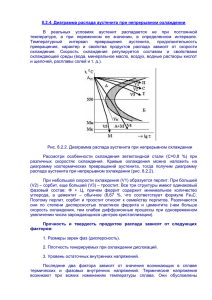
Диссертация на соискание ученой степени кандидата физико
advertisement

ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ На правах рукописи ИСУПОВА ИРИНА ЛЕОНИДОВНА ДВУХУРОВНЕВАЯ МОДЕЛЬ ПОВЕДЕНИЯ СТАЛЕЙ ПРИ ТЕРМОМЕХАНИЧЕСКИХ ВОЗДЕЙСТВИЯХ С УЧЕТОМ ФАЗОВЫХ ПРЕВРАЩЕНИЙ 05.13.18 – Математическое моделирование, численные методы и комплексы программ Диссертация на соискание ученой степени кандидата физико-математических наук Научный руководитель доктор физико-математических наук, профессор Трусов Петр Валентинович Пермь – 2014 Содержание Сокращения и основные обозначения…………………………………………...4 Введение…………………………………………………………………………...7 1. Подходы и методы исследования поведения сталей при термомеханических воздействиях……………………………………………………………… 15 1.1. Обзор результатов экспериментальных исследований превращения аустенита при охлаждении……………………………………………………...15 1.2. Существующие модели для описания поведения сталей при термомеханических нагружениях с учетом фазовых превращений………………..23 1.3. Построение конститутивных моделей материалов с использованием внутренних переменных…………………………………………………….34 2. Двухуровневая модель для описания поведения сталей при термомеханических нагружениях с учетом фазовых превращений……………………….. 36 2.1. Структура двухуровневой модели…………………………………..36 2.2. Математическая постановка задачи………………………………...44 2.2.1. Постановка задачи на макроуровне I………………………44 2.2.2. Определение напряженно-деформированного состояния. Постановка задачи на макроуровне II…………………………….46 2.2.3. Определение напряженно-деформированного состояния и фазового состава. Постановка задачи на мезоуровне……………47 2.2.4. Постановка задачи теплопроводности для представительного макрообъема…………………………………………………….55 2.2.5. Постановка задачи диффузии для представительного макрообъема……………………………………………………………57 2.3. Согласование соотношений моделей различных масштабных уровней……………………………………………………………………………….. 58 2.3.1. Согласование для задачи определения напряженно- деформированного состояния……………………………………..58 2.3.2. Согласование для задачи теплопроводности………………64 2 3. Кинетическое уравнение для определения объемных долей сосуществующих фаз…………………………………………………………………………...67 3.1. Вывод кинетического уравнения для определения изменения объемной доли в рамках термодинамики необратимых процессов…………….. 67 3.2. Определение свободной энергии многофазной системы………….74 4. Алгоритм реализации модели………………………………………………..78 4.1. Общая структура алгоритма реализации двухуровневой модели...78 4.2. Алгоритм решения задачи теплопроводности для представительного объема макроуровня…………………………………………………………82 4.3. Алгоритм решения задачи диффузии для представительного объема макроуровня………………………………………………………………….85 4.4. Определение фазового состава и напряженно-деформированного состояния на мезоуровне………………………………………………………..86 5. Анализ результатов вычислительных экспериментов с использованием двухуровневой модели…………………………………………………………..92 5.1. Идентификация и верификация модели на примере мартенситного превращения при деформировании стали AISI 304…………………………...94 5.2. Моделирование поведения стали AISI 301 при простом и сложном нагружении с учетом мартенситных превращений………………………….101 5.3. Моделирование поведения стали с учетом диффузионного ферритного превращения………………………………………………………….......115 Заключение……………………………………………………………………..121 Литература……………………………………………………………………...123 3 СОКРАЩЕНИЯ ГЦК (решетка) – гранецентрированная кубическая (решетка) ЛСК – лабораторная система координат (декартова ортогональная система координат единая для всех конфигураций) МДТТ – механика деформируемого твердого тела МКЭ – метод конечных элементов НДС – напряженно-деформированное состояние ОС – определяющие соотношения ОЦК (решетка) – объемно-центрированная кубическая (решетка) ОЦТ (решетка) – объемно-центрированная тетрагональная (решетка) ПО – представительный объем СК – система координат СС – система скольжения 4 ОСНОВНЫЕ ОБОЗНАЧЕНИЯ CR cr , – обозначение коротационной производной на макроуровне и мезоуровне e , r in – индексы, обозначающие упругую и неупругую составляющие – индекс, обозначающий величины, характеризующие относитель- ное движение, фиксируемое подвижным наблюдателем в жесткой подвижной системе отсчета t – время (или его аналог) I – единичный тензор Обозначения величин мезоуровня c p – концентрация p-го легирующего элемента e – внутренняя энергия f – свободная энергия Гиббса g – скрытая теплота фазового превращения i – индекс, обозначающий принадлежность величины к конкретной фазе n – общее число систем скольжения кристаллита s – энтропия y – мощность внутреннего теплового источника ( k ) – сдвиг по k-й системе скольжения – температура – теплоемкость – объемная доля ( k ) – касательное напряжение в k-й системе скольжения c( k ) – критическое напряжение k-й системы скольжения c( k0 ) – начальное критическое напряжение k-й системы скольжения 5 b k – единичный вектор по направлению вектора Бюргерса k-й системы скольжения n – единичная нормаль k-й системы скольжения k d p – тензор диффузии p-го легирующего элемента d p – тензор термодиффузии p-го легирующего элемента q – мера деформированного состояния α – тензор термического расширения ζ – мера скорости деформации λ – тензор термического расширения o – тензор поворота, совмещающий лабораторную систему координат с системой координат, связанной с решеткой аустенита σ – несимметричный тензор напряжений Коши п – тензор упругих свойств Обозначения величин макроуровня – теплоемкость M – число зерен, входящих в представительный макрообъем Y – мощность внутреннего теплового источника – температура B – вектор распределенных объемных сил G – вектор теплового потока T – вектор поверхностных сил Q – мера деформированного состояния Ζ – мера скорости деформации Α – тензор термического расширения Λ – тензор термического расширения Σ – тензор напряжений Коши Π – тензор упругих свойств 6 Введение Фазовые превращения в сталях относятся к твердотельным полиморфным превращениям, которые протекают с изменением кристаллической структуры [22, 31, 40, 44]. Если материал может существовать в различных кристаллических модификациях, то при данных условиях более устойчива та фаза, кристаллическому строению которой соответствует более низкий уровень свободной энергии. При этом тип решетки, получаемый в результате фазового превращения, зависит от сложного взаимодействия атомов, электронов и т. д., детальное исследование которого выходит за рамки настоящей работы. Применение термодинамики позволяет связать устойчивость той или иной кристаллической модификации с силами связи, амплитудой и частотой колебаний атомов, которые, естественно, определяются особенностями строения и состояния атомов. Полиморфные превращения подчиняются общим закономерностям кристаллизационных процессов, связанных с возникновением и ростом зародышей новой фазы. Полиморфные превращения происходят в твердой анизотропной среде, поэтому в процессе превращения на соприкасающихся гранях исходной и новой фаз атомы, принадлежащие различным модификациям, занимают положения согласно принципу структурного и размерного соответствия: зародыш новой фазы в твердой анизотропной среде должен быть ориентирован так, чтобы он сопрягался с исходной («старой») фазой кристаллическими плоскостями, наиболее близкими по структурным размерам [11, 24]. Полиморфные превращения протекают следующим образом: в условиях, определяющих термодинамическую устойчивость новой фазы, благодаря флуктуациям энергии, конфигурации или плотности (концентрации) образуется устойчивый зародыш, характеризующийся иным расположением атомов, определяющим новую кристаллическую решетку. В соответствии с принципом структурного и размерного соответствия порядок расположения атомов изменяется путем закономерного их перемещения в решетке исходной фазы, при котором достигается минимум энергии 7 при данном объеме превращенного вещества [60]. Такой механизм образования новой фазы при полиморфном превращении в твердой анизотропной среде приводит к тому, что кристаллы новой модификации оказываются закономерно ориентированными по отношению к исходным кристаллам. При полиморфном превращении изменяется и зеренная структура материала, что связано с образованием зерен новой фазы, отличающихся по форме и размерам от зерен исходной фазы. Такое изменение микроструктуры при полиморфных превращениях используется в ряде технологических процессов термомеханической обработки сплавов (отжиг второго рода, закалка и т. д.). Термомеханическая обработка сталей является важнейшей частью всех технологических процессов производства металлических изделий. Целью такой обработки является создание необходимого набора физико-механических свойств материала, улучшение его обрабатываемости при изготовлении изделий. В сталях наблюдаются все известные для твердого состояния фазовые превращения, происходящие при охлаждении аустенита: перлитное, промежуточное (бейнитное) и мартенситное. Превращение может осуществляться, как по так называемому нормальному/диффузионному (если межфазная граница некогерентная), так и по мартенситному/бездиффузионному (если межфазная граница когерентная) механизмам. Важной особенностью диффузионных превращений является то, что образование новой фазы сопровождается перераспределением легирующих элементов и углерода, требующим диффузионного перемещения атомов на дальние расстояния. Аустенит представляет собой твердый раствор внедрения углерода в Fe , а мартенсит – пересыщенный твердый раствор замещения в Fe , возникающий в результате превращения при отсутствии диффузии углерода. В результате пер- литного и промежуточного превращений образуются сложные структуры. Так, перлит представляет собой эвтектоидную смесь Fe (феррита) и цементита или специальных карбидов. Бейнитная структура может включать следующие составляющие: феррит, карбиды и остаточный аустенит. Возможность протекания тех или иных фазовых превращений при термомехани8 ческих воздействиях и их кинетика зависят от таких параметров, как температура, условия нагрева, длительность выдержки, скорость охлаждения, механическая нагрузка и т. п. Например, отжиг второго рода [10, 35, 55] характеризуется аустенитным превращением, происходящим в условиях перегрева выше температуры эвтектоидного превращения сталей с перлитной структурой. При таком перегреве практически мгновенно появляются зародыши аустенита, растущие в дальнейшем по диффузионному механизму. Развитие зародыша аустенита ведет к «растворению» пластин цементита и феррита. При закалке сталей [1, 3, 10, 35, 37] быстрое охлаждение с температуры высокотемпературной аустенитной фазы обратное диффузионное превращение подавляется и происходит процесс перестройки решетки, который обусловлен явлением полиморфизма. Таким образом, при закалке сталей превращение происходит по так называемому бездиффузионному (мартенситному) механизму. Хорошо известным является факт, что процессы термомеханической обработки сталей не могут происходить без существенной эволюции микроструктуры (изменение дефектной структуры, фазового состава) и мезоструктуры (разворот кристаллических решеток отдельных зерен). Мезо- и микроструктура материала существенным образом эволюционирует в процессе термомеханического воздействия. Так, макровоздействия приводят к эволюции мезо- и микроструктуры, а изменение мезо- и микроструктуры определяет, каким образом материал будет вести себя на макроуровне. Корректное описание изменения структуры материалов, в том числе и за счет протекающих фазовых превращений, дает возможность разработки новых методов получения материалов с заданным набором свойств и оптимизации уже существующих материалов и технологий их обработки. Экспериментальное исследование данного вопроса является достаточно ресурсоемким, в особенности – в случае сложного термомеханического нагружения, поэтому в механике деформируемого твердого тела (МДТТ) актуальной становится задача по- 9 строения моделей, описывающих состояние и эволюцию структуры материала с учетом твердотельных фазовых превращений. При построении конститутивных моделей материалов эволюцию мезои микроструктуры можно рассматривать как неявно, так и явно [53]. При использовании первого подхода в определяющие соотношения (ОС) над историей макровоздействий приходится вводить сложные операторы, без введения параметров, описывающих собственно эволюцию мезо- и микроструктуры. Механизмы процесса деформирования, которые в первом случае, описываются различными операторами модели, сложно выявить и обосновать. В последнее время все чаще применяется второй подход, связанный с введением внутренних переменных, т. е. параметров, позволяющих описывать состояние и изменение мезо- и микроструктуры, и с записью эволюционных уравнений для них [46, 47]. Модели, основанные на введении в их структуру внутренних переменных, по существу являются многоуровневыми, т.е. процессы деформирования и фазовых превращений рассматриваются на более низких масштабных уровнях по сравнению с макроуровнем, что позволяет ввести в рассмотрение присущие этим уровням механизмы деформирования и фазовых превращений. Необходимое число уровней выбирается в соответствии со структурой материала. Весьма важной в многоуровневых моделях является гипотеза о связи характеристик различных масштабных уровней. При построении многоуровневых моделей для описания поведения сталей при термомеханических воздействиях с учетом фазовых превращений мало внимания уделяется вопросу перехода от величин нижнего масштабного уровня на верхний масштабный уровень, и обычно используются самые простые гипотезы [70, 83, 89], однако именно гипотеза о связи характеристик различных уровней во многом определяет «качество модели». Не менее важным при построении многоуровневых моделей является вопрос о теориях, положенных в основу нижних масштабных уровней. Часто 10 для моделирования фазовых превращений используются модели, основанные на физических теориях пластичности, дополнительно учитывающие происходящие фазовые превращения [105, 113]. Здесь физические теории пластичности – многочисленный класс теорий, в основе которых лежит рассмотрение в явной форме процессов деформирования и фазовых превращений на мезо- и микромасштабах. В большинстве работ, применяющих данный подход, используются симметричные меры напряженного и деформированного состояния, что приводит к ситуациям, противоречащим физике процесса деформирования [4, 48]. Отдельным вопросом является описание упрочнения с учетом происходящих в материале фазовых превращений. Из экспериментов известно, что образование новой фазы сказывается на развитии пластической деформации в родительской фазе, поэтому сопротивление сдвигу должно зависеть от изменения объемной доли новой фазы. Пластическая же деформация родительской фазы может значительно влиять на свойства образующейся фазы через наследование последней дислокационной структуры родительской фазы. Таким образом, создание математических моделей для описания поведения сталей при термомеханическом нагружении с учетом фазовых превращений, в которых применяются несимметричные меры напряженного и деформированного состояния и учитывается изменение микро- и мезоструктуры материала, является весьма актуальным. Целью работы является разработка, исследование и реализация математической модели для описания поведения сталей при термомеханических воздействиях с учетом фазовых превращений, которая позволяла бы качественно и количественно адекватно описывать изменение мезо- и микроструктуры материала, а также физико-механических характеристик. Задачи работы: разработка двухуровневой модели для описания поведения сталей при термомеханических воздействиях с учетом фазовых превращений с исполь- 11 зованием несимметричных мер напряженного и деформированного состояния на мезоуровне; получение и обоснование условий согласования ОС различных мас- штабных уровней и способа определения явных внутренних переменных модели на каждом уровне; разработка процедуры идентификации и верификации модели; создание комплекса программ для проведения вычислительных экспе- риментов при произвольном термомеханическом нагружении. Научная новизна работы заключается в следующем: Разработана двухуровневая математическая модель для описания пове- дения сталей при термомеханических воздействиях с использованием несимметричных мер напряженного и деформированного состояния на мезоуровне, позволяющей учесть предысторию нагружения по средствам использования внутренних переменных и эволюционных соотношений для них на каждом из рассматриваемых масштабных уровней. Разработан алгоритм реализации модели для каждого из масштабных уровней, обеспечивающий выполнение условий согласования ОС различных уровней. Проведена идентификация и верификация модели на примере исследо- вания мартенситного превращения при одноосном растяжении образца стали AISI 304. Проведены численные эксперименты по моделированию поведения стали AISI 301 при простом и сложном нагружении с учетом мартенситных превращений на макроуровне II и мезоуровне. Получены результаты моделирования поведения стали с учетом диффузионных превращений для представительного объема (ПО) макроуровня. На защиту выносятся: Двухуровневая математическая модель для описания поведения сталей при термомеханических воздействиях с учетом фазовых превращений. 12 Математическая модель мезоуровня для описания неупругого деформи- рования, основанная на применении несимметричной упруговязкопластической физической теории, учитывающей фазовые превращения. Модификация закона упрочнения СС, учитывающая дополнительное упрочнение за счет фазового превращения. Способ согласования соотношений различных масштабных уровней. Результаты моделирования некоторых процессов термомеханической обработки. Структура и объем работы. Диссертационная работа состоит из списка сокращений и обозначений, введения, 5 глав, заключения, списка использованной литературы. Работа содержит 39 рисунков, библиографический список – 116 наименований, изложена на 134 страницах. Во введении проводится обоснование актуальности выбранной темы, представлена общая характеристика рассматриваемой задачи, описана структура диссертационной работы. Первая глава носит обзорный характер. В ней приводится анализ теоретических и экспериментальных работ по исследованию превращений в сталях при охлаждении аустенита и моделей для описания поведения сталей при термомеханических воздействиях с учетом фазовых превращений, рассматривается подход к построению ОС, в основе которого лежит использование в структуре модели на каждом из рассматриваемых масштабных уровней параметров, называемых внутренними переменными, описывающих микроструктуру материала, и являющихся носителями информации о предыстории воздействия. Вторая глава посвящена рассмотрению разрабатываемой математической модели для описания поведения сталей при термомеханических воздействиях с учетом фазовых превращений. Представлена общая структура двухуровневой модели (мезо- и макроуровни), осуществляется выбор несимметричных мер скорости деформации и напряжений. Для облегчения постановки и последующего решения связанная задача «расщепляется» на отдельные 13 подзадачи, а именно: задачу определения напряженно-деформированного состояния (НДС), температурную задачу, задачу диффузии и задачу определения фазовых долей всех сосуществующих фаз. Для этих задач используются различные типы моделей. Для указанных задач приводятся содержательная, концептуальная и математическая постановки на всех масштабных уровнях. Обсуждаются вопросы согласования ОС на различных масштабных уровнях. В третьей главе приведены необходимые положения неравновесной термодинамики в формулировке Онзагера, на основании которых получено кинетическое уравнение для определения изменения объемной доли фаз при различных видах превращений. Обосновывается использование энтропии в качестве термодинамической функции состояния в кинетическом уравнении, определяются независимые параметры, от которых зависит энтропия. Для удобства моделирования в кинетическом уравнении производится переход от энтропии к функции свободной энергии. Подробно рассмотрен также вопрос определения свободной энергии многофазной системы. В четвертой главе для всех масштабных уровней предлагаемой модели рассмотрены алгоритмы численной реализации и вопросы, связанные с ними. В пятой главе представлены результаты численных экспериментов с использованием разработанной модели. Рассмотрены эксперименты на простое и сложное нагружение ПО макроуровня материала. В заключении приведены основные выводы по работе и результаты. Доверенность результатов подтверждается удовлетворительным соответствием между результатами расчета и экспериментальными данными. Практическая ценность работы заключается в возможности применения предлагаемой модели (включая разработанную программу реализации модели) для разработки новых и оптимизации существующих процессов термомеханической обработки сталей, позволяющей описывать при этом эволюцию микроструктуры и, следовательно, прогнозировать поведение материала на макроуровне. 14 1. Подходы и методы исследования поведения сталей при термомеханических воздействиях 1.1. Обзор результатов экспериментальных исследований превращения аустенита при охлаждении В системах Fe – C и Fe – Me – C могут происходить все известные твердотельные фазовые превращения: перлитное, промежуточное (бейнитное) и мартенситное. На рис. 1 в качестве примера представлены диаграммы изотермического превращения для различных марок стали. Рис. 1. Диаграммы изотермического превращения сталей: а – 40ХНМ, б – 18Х2Н4В, в – 30Х13, г – с 0.9% С. А – аустенит, Ф – феррит, К – карбид, П – перлит, II ст. – промежуточное (бейнитное) превращение, М – мартенсит [31] Одна из особенностей этих систем заключается в сильно различающейся диффузионной подвижности металлических атомов и атомов углерода. При превращениях переохлажденного аустенита перестройка гране- центрированной кубической (ГЦК) решетки в объемно-центрированную кубическую (ОЦК) (объемно-центрированную тетрагональную (ОЦТ)) может 15 происходить одновременно с диффузионным перераспределением углерода и легирующих элементов. Фазовый переход может осуществляться по двум механизмам: мартенситному (если межфазная граница когерентная) и нормальному (если межфазная граница некогерентная) (рис. 2). Рис. 2. Схема расположения атомов на границе растущего кристалла при сохранении когерентности решеток (а) и при нарушении ее (б) [31] Рассмотрение закономерностей превращения аустенита приводит к необходимости учета особенностей твердофазного состояния. В этом случае сильное межатомное взаимодействие является причиной возникновения полей упругих напряжений при превращении. Снижение упругой энергии деформации, к которому стремится система, обусловливает наличие различных релаксационных механизмов, влияющих на форму, ориентировку, взаимное расположение и внутреннюю структуру кристаллов новой фазы. Мартенситное превращение Мартенситное превращение в большинстве сплавов и сталей происходит при высоком уровне переохлаждения [25-27]. Однако есть материалы, например, TRIP-стали, в которых мартенситное превращение происходит при комнатной температуре при деформировании. Образование мартенсита протекает по бездиффузионному механизму, его химический состав остается таким же, как и у исходного аустенита. Мартенсит в углеродистых сталях представляет собой пересыщенный твердый раствор углерода в -железе. Он образуется в результате упорядоченного кооперативного перемещения атомов на расстояния существенно меньшие, чем межатомные. Так как смещение атомов осуществляется в строго определенных направлениях, то в итоге 16 возникает макроскопический сдвиг, проявляющейся в появлении рельефа на полированной поверхности образца. Большинство исследователей считают, что зарождение мартенсита происходит гетерогенным путем. При этом кристаллы формируются внутри зерна исходной фазы. Наиболее предпочтительными местами зарождения мартенсита являются дислокации и дефекты упаковки, наличие которых облегчает сдвиговую деформацию в решетке, что уменьшает работу зарождения мартенсита, при этом дислокации могут служить готовой границей растущего кристалла. Важнейшей чертой мартенситного превращения является его распространение на широкий интервал температур. Так, каждой температуре, лежащей ниже точки начала превращения, соответствует определенное количество мест, которые могут служить зародышами новой фазы, а по исчерпании этих мест превращение прекращается, и для того, чтобы появились новые потенциальные места зарождения, необходимо увеличивать термодинамический стимул, т. е. понижать температуру. Обычно после завершения мартенситного превращения остается некоторая доля непревращенного аустенита. Наиболее просто бездиффузионная трансформация решетки при мартенситном превращении описывается с использованием деформации Бейна (рис. 3). Рис. 3. Схема перестройки решетки ГЦК в решетку ОЦК. Жирными линиями в решетке ГЦК выделена тетрагональная ячейка, которая при деформации Бейна превращается в решетку мартенсита. В решетке ГЦК указаны не все атомы. На рис. 3, а приведены две СК для решеток ГЦК и ОЦК. Оси деформации Бейна: а 001 , б 100 , в 010 [43] Экспериментально установлено, что кристаллическая решетка образующегося мартенсита имеет определенную ориентацию по отношению к решетке 17 исходной фазы. Основными ориентационными соотношениями, описывающими перестройку ГЦК решетки в ОЦК, являются соотношения Курдюмова– Закса [85] и Нишиямы [96]. Схема Курдюмова–Закса также может быть использована для описания получения решетки ОЦТ, однако в этом случае величины сдвигов должны быть немного меньше тех, которые переводят решетку ГЦК в ОЦК [14, 84]. При росте пластины мартенсита можно выделить плоскость раздела пластины с матрицей, которая не искажается и не вращается – габитусную (инвариантную) плоскость. Инвариантность плоскости раздела фаз при перестройке решетки может быть достигнута при наличии дополнительной деформации за счет скольжения или двойникования (рис. 4) [2]. Рис. 4. Виды деформации при мартенситном переходе (штриховая линия – граница раздела фаз): а – исходный недеформированный участок кристалла; б – изменение формы участка при превращении; в – восстановление формы участка скольжением; г – восстановление формы участка двойникованием [43] В сталях различного состава кристаллы мартенсита могут отличаться друг от друга по форме, структуре и способам объединения в ансамбли [6, 56, 61]. Наиболее распространенной является классификация типа мартенсита по его морфологическим признакам: реечный, баттерфляй, пластинчатый (линзовидный). Мартенситное превращение может протекать как в атермических, так и в изотермических условиях [43]. Атермический механизм наблюдается в сталях, точка начала превращения для которых лежит существенно выше комнатной температуры, и происходит без инкубационного периода практически мгновенно, распространяясь на широкую область температур. Понижение температуры приводит к плавному увеличению количества мартенсита. Приостановка охлаждения вызывает практически полное прекращение превращения. При небольшом переохлаждении ниже температуры начала превра18 щения процесс может получать незначительное развитие и в изотермических условиях. Изотермическое превращение начинается по истечении инкубационного периода и его объемная скорость сначала возрастает, достигая максимума, а затем снижается. При изотермической кинетике рост отдельных кристаллов происходит с большой скоростью и не зависит от температуры. Однако количество образовавшегося при этом мартенсита обычно не превышает нескольких процентов, а само превращение быстро затухает. В решетке ОЦК атомы углерода занимают октаэдрические поры (рис. 5) [8]. Атомы углерода упорядоченно располагаются вдоль одного из направлений типа <001>, в результате чего решетка мартенсита становится тетрагональной. Рис. 5. Расположение атомов углерода в ячейке мартенсита [43] Полиморфное («нормальное») γα превращение При «нормальном» превращении смещение атомов на границе фаз, приводящее к перестройке кристаллической решетки, не является строго упорядоченным. Для перехода атомов в новые стабильные положения необходима энергия тепловых колебаний, сравнимая с той, которая нужна для самодиффузии. На начальной стадии процесса появляются зернограничные выделения, а после завершения превращения образуются приблизительно равновесные (полиэдрические) зерна α – фазы с малой плотностью дислокаций. Полиморфное превращение не вызывает появление характерного микрорельефа на полированной поверхности шлифа [94]. Изотермическое «нормальное» превращение характеризуется наличием инкубационного периода и 19 его температурной зависимостью, сравнительно малой скоростью и протеканием превращения до исчерпания исходной фазы [23]. При определенных условиях в сталях с 0.4-0.5% углерода феррит выделяется в виде правильно ориентированных пластин – видманштеттов феррит. Образование видманштеттова феррита может происходить внутри аустенитного зерна, при этом часто возникают группы с параллельным расположением пластин [9, 29, 42]. Пластины могут расти и от ферритной сетки, сформировавшейся до их появления. Выделение видманштеттова феррита сопровождается появлением рельефа на полированной поверхности шлифа. Образование его пластин происходит кристаллографически упорядоченно. Установлено, что ориентационное соотношение видманштеттова феррита и исходного аустенита близко к ориентационному отношению Курдюмова– Закса. Перлитное превращение Перлит представляет собой эвтектоидную смесь кристаллов α – фазы (феррита) и цементита или специальных карбидов. Формирование перлита начинается с появления зародыша либо феррита, либо цементита [75]. Обычно перлитная колония зарождается на границе зерна аустенита или на границе ранее выделившихся избыточных фаз: феррита в до- и цементита – в заэвтектоидной стали. При возникновении зародыша цементита и его последующем росте аустенит в соседних областях обедняется углеродом и создаются благоприятные условия для зарождения феррита. Затем около зародыша цементита появляются зародыши ферритной фазы. При росте зародышей феррита окружающий аустенит обогащается углеродом, так как равновесная концентрация углерода в феррите мала. Повышенная концентрация углерода в областях аустенита, прилегающих к ферритным участкам, облегчает образование новых зародышей цементита. Образовавшиеся участки новой фазы ограничены с боков участками другой фазы, поэтому их рост вглубь аустенита приводит к образованию пластин, в результате чего формируются колонии пластинчатого перлита. Если в аустенитной структуре вначале возникает за20 родыш феррита, то при его росте прилегающий к нему аустенит начинает обогащаться углеродом, что приводит к выделению с двух его сторон пластин цементита. Далее превращение будет развиваться по сценарию, описанному выше. Боковой рост перлитной колонии происходит путем многократного образования пластин феррита и цементита. Фронтальный рост перлитной колонии происходит за счет кооперативного удлинения пластин обеих фаз, перед торцами которых возникает градиент концентрации углерода в аустените. Пластины могут изменять направление роста, например, вследствие дефектов структуры аустенита. На рис. 6 приведена схема зарождения и роста перлитных колоний. Рис. 6. Схема зарождения и роста перлитных колоний [43] В пределах перлитной колонии пластины одной фазы имеют единую кристаллографическую ориентировку. Кроме того, взаимная ориентация феррита и цементита соответствует вполне определенным ориентационным соотношениям, обеспечивающим минимум упругой и поверхностной энергии при превращении (ориентационные соотношения Багаряцкого и ориентационные соотношения Питча) [15, 45]. Также в переделах одной перлитной колонии существует ориентационная связь между структурными составляющими перлита и первоначальным аустенитом [99]. Появление перлита фиксируется после определенного инкубационного периода, в течение которого происходят процессы подготовки, заключающиеся в изменении взаимного расположения атомов различных элементов и, вероятно, образовании их кластеров. Сначала скорость образования перлита мала, но постепенно она увеличивается и достигает максимума примерно при 21 50% продуктов распада. Затем превращение затухает и при достаточной выдержке завершается полным распадом переохлажденного аустенита. Промежуточное (бейнитное) превращение Промежуточное (бейнитное) превращение аустенита протекает в интервале температур, ограниченном сверху областью диффузионного, а снизу – мартенситного превращения [41, 59, 112]. Оно обладает чертами как диффузионного, так и бездиффузионного превращений. В результате промежуточного превращения в стали формируется так называемая бейнитная структура, которая в общем случае может состоять из следующих составляющих: бейнитного феррита, карбидов и остаточного аустенита. Распад переохлажденного аустенита в области промежуточного превращения начинается после инкубационного периода, как и в случае диффузионного распада. При изотермической выдержке скорость превращения сначала возрастает, достигая максимума, а затем уменьшается, но в отличие от диффузионного превращения максимальная скорость приходится на начало процесса. Промежуточное превращение, как и мартенситное, не идет до конца. Развитие промежуточного превращения, в отличие от мартенситного, происходит за счет образования новых и подрастания уже существующих кристаллов. Промежуточное превращение, как и мартенситное, сопровождается образованием рельефа на полированной поверхности шлифа, что свидетельствует о сдвиговом характере перестройки кристаллической решетки. Ориентационные соотношения между бейнитным ферритом и аустенитом не зависят от содержания углерода в стали и температуры промежуточного превращения и близки к соотношениям для мартенсита [80]. Бейнитный феррит представляет собой слабо пересыщенный по углероду твердый раствор, следовательно, решетка этой фазы имеет определенную тетрагональность. По особенностям микроструктуры различают верхний и нижний бейнит. Наиболее распространенным является представление о том, что при образовании бейнитного феррита из аустенита имеет место сдвиговой мартенситный механизм с сохранением когерентной связи кристаллических ре22 шеток исходной и новой фаз. При этом образование бейнитного феррита связано с перераспределением углерода в аустените. При пониженных температурах такой процесс практически более выгоден, чем карбидообразование, т.к. не требует резкой дифференциации по углероду. Флуктуационное перераспределение углерода является причиной появления участков аустенита с его пониженной концентрацией, в которых в итоге и происходит мартенситное превращение. Для того, чтобы образованные участки -фазы росли, необходим процесс отвода атомов углерода внутрь аустенита от межфазной границы. Процесс отвода протекает с относительно небольшой скоростью и ограничивает скорость роста бейнитного феррита. Промежуточное превращение никогда не происходит до полного исчерпания родительской фазы, т. к. непревращенный аустенит в процессе превращения обогащается углеродом. Особенности развития карбидообразования зависят от температуры промежуточного превращения. При температуре образования верхнего бейнита карбид непосредственно выделяется из аустенита, находящегося вблизи границы бейнитного феррита. В этом случае диффузия углерода происходит с достаточно высокой скоростью, поэтому аустенит сильно обогащается им. При температуре образования нижнего бейнита карбид выделяется и из феррита, т. к. бейнитный феррит заметно пересыщен углеродом. Из приведенного обзора результатов экспериментальных исследований превращения аустенита при охлаждении видно, что механизм и кинетика полиморфного превращения определяют особенности различных типов превращений, в результате которых могут образовываться достаточно сложные структуры. Возможность протекания тех или иных фазовых превращений зависит от состава стали и параметров термомеханического воздействия. 1.2. Существующие модели для описания поведения сталей при термомеханических нагружениях с учетом фазовых превращений Сегодня в литературе имеется большое число работ, посвященных построению моделей для описания поведения сплавов и сталей при термомеха23 нических нагружениях, учитывающих фазовые превращения. Можно выделить два основных подхода к построению таких моделей. Первый подход связан с явным введением межфазных границ с рассмотрением условий на них и кинетики фазового перехода. Второй подход связан с введением в модель параметров состояния (например, концентрации новой фазы), которые характеризуют в «среднем» особенности структуры. Для определения этих параметров формулируются специальные соотношения. Краткий обзор работ, посвященных математическому моделированию поведения сплавов и сталей с учетом как бездиффузионных (мартенситных), так и диффузионных фазовых превращений можно найти в статье [17]. Ниже рассматриваются некоторые модели, выделенные на основе потенциальной возможности развития используемых в них подходов для более точного описания фазовых превращений при термомеханических воздействиях. Явное введение в рассмотрение межфазных границ [7, 57] позволяет описывать фазовые превращения с точки зрения МДТТ с использованием идей классической теории фазовых переходов Дж. Гиббса. Межфазная граница рассматривается как поверхность, на которой деформации при непрерывном поле перемещений претерпевают разрыв. Изменяющаяся в процессе фазового перехода микроструктура материала порождает изменение модулей упругости и собственные деформации превращения, поэтому область, содержащую новую фазу, можно считать неоднородностью, на границе которой некоторые компоненты тензора деформации могут претерпевать разрыв. Для того, чтобы в упругом теле возникло равновесное разрывное поле деформаций, в пространстве деформаций необходимо существование областей, где неравенство Адамара, являющееся необходимым условием устойчивости по отношению к бесконечно малым возмущениям, нарушается. В случае равновесия на границе фаз ставятся следующие условия: сохранения сплошности, непрерывности усилия и термодинамическое условие, которое является аналогом равенства химических потенциалов в теории Гиббса. Последнее условие накладывает ограничения на форму межфазной границы и деформации 24 на ней, т. к. даже если определяющие соотношения (ОС) позволяют учитывать существование двухфазных состояний, не любые деформации могут иметь место на границе фаз. Это приводит к понятию зоны фазовых переходов, граница которой в пространстве деформаций определяет предельную поверхность превращения. Кратко остановимся на моделях, основанных на введении параметра, характеризующего фазовый состав материала (например, фазовая доля), и формулировке кинетического соотношения для него. Метод фазового поля довольно часто применяется для моделирования как диффузионных [90, 92, 103], так и бездиффузионных (мартенситных) [62, 63, 111, 114] фазовых превращений. Данный подход [68] предполагает наличие «размытой», «диффузионной» границы между фазами в отличие от классических методов, использующих понятие «резкой границы» (когда многофазная структура описывается положением границы и для каждой из областей множество дифференциальных уравнений решается совместно с уравнениями потока и конститутивными уравнениями на границе). В подходе «диффузионной границы» форма и взаимное расположение областей, занимаемых отдельными фазами, описываются совокупностью параметров, определяющих доли фаз [69, 111]. Значение параметра может изменяться от 0 (соответствует области, где нет рассматриваемой фазы) до 1 (соответствует однофазной области), поэтому микроструктуру (за исключением границ зерен, дефектов и т.п.) можно описать множеством однофазных областей, разделенных границами, на которых более одного значения доли фаз отлично от нуля. Таким образом, в подходе «диффузионной границы» изменение формы областей (а значит – и положения границы) с течением времени неявно определяется изменением долей фаз. Изменение во времени долей фаз описывается кинетическим уравнением, получаемым в рамках термодинамики необратимых процессов, т. е. используется линейная связь скорости изменения долей фаз и производной термодинамического потенциала по данному параметру. Чаще всего исследуются фазовые превращения, происходящие в изо25 термических условиях, и в качестве термодинамического потенциала берется свободная энергия, но есть работы по изучению и неизотермических процессов, когда в качестве термодинамического потенциала выбирается энтропия [28, 91]. Термодинамический потенциал обычно определяется суммой химической, упругой и «градиентной» составляющих. Для решения задач чаще всего используется метод конечных элементов (МКЭ), а в качестве моделируемой области выступает объем, состоящий из нескольких зерен. С помощью метода фазового поля можно получить детальную информацию о внутренней структуре материала, но для моделирования процессов термомеханической обработки реальных изделий этот метод малопригоден из-за огромных вычислительных затрат. Для описания процессов фазовых превращений при термомеханической обработке сталей на уровне целых конструкций часто используются кинетические макромодели. Для определения объемной доли фаз используются феноменологические соотношения, такие, как уравнения Koistinen and Marburger [82], Johnson-Mehl-Avrami-Kolmogorov [64] и т. п. Большинство этих соотношений получено при некоторых существенных допущениях. Для деформаций (скоростей деформаций) принимается гипотеза аддитивности упругих, пластических, температурных, трансформационных составляющих и неупругой составляющей, обусловленной фазовыми превращениями для сталей, проявляющих TRIP – эффект (пластичность, наведенная фазовым (обычно мартенситным) превращением) [73, 93]. Интерес к этим сталям объясняется их повышенной прочностью и одновременно пластичностью, т.е. при равной прочности (пределе текучести) TRIP-стали обладают в 2-3 раза большей пластичностью, что обеспечивают им преимущества в процессах штамповки и формования. Отмеченные свойства прочности и пластичности TRIP-сталей, с одной стороны, являются результатом неупругой деформации, сопровождающей превращение, а с другой – действия внутренних напряжений изменяющейся фазы, приводящих к дополнительному пластическому течению (TRIP-эффект). При описании неупругого деформирования исполь26 зуются достаточно простые модели, в которых отсутствует прямое включение механизмов деформирования и фазовых превращений и их носителей, существующих на разных масштабных уровнях в реальном материале. Обычно для решения поставленной связанной нелинейной краевой задачи используется численная процедура, организованная как последовательность решения задач теплопроводности и упругопластичности с использованием метода конечных элементов (МКЭ). В последние годы для моделирования мартенситных превращений все чаще используются модели, основанные на физической теории пластичности, дополнительно учитывающие происходящие фазовые превращения (градиент места, помимо упругой и пластической составляющих, включает составляющую, которая отвечает за изменение конфигурации вследствие фазового превращения) [105, 113]. Кинетика фазового превращения описывается с использованием кристаллографической теории мартенситных превращений. Соотношения для движущих сил фазового превращения и пластического деформирования получены на основе неравенства диссипации. При получении этих соотношений учитывается вклад от поверхностной энергии и энергии дефектов, связанный с наличием инвариантной плоскости и дислокаций соответственно. В работе [108] предложена многоуровневая модель для описания фазового перехода «аустенит – мартенсит». В рассмотрение вводятся следующие масштабные уровни: мезо-, верхний микро- и нижний микроуровень. Верхний микроуровень включает пластины мартенсита (в окружении остаточного аустенита), которые, в свою очередь, состоят из чередующихся сдвойникованных вариантов мартенсита – элементов нижнего микроуровня. Для сдвойникованных пар пластинок вводится понятие «трансформационной системы», характеризуемой нормалью к габитусной плоскости и средним вектором сдвига, который определяется по градиенту места трансформационной системы. Кинематические соотношения как на верхнем микроуровне, так и на мезоуровне основаны на мультипликативном разложении градиента места 27 на упругую и трансформационную составляющие. Определяющие соотношения (ОС) получаются последовательным осреднением с нижнего микроуровня. Термодинамическое описание процесса фазового превращения основано на принципах, описанных выше. Работа [86] посвящена моделированию поведения сталей, обладающих TRIP-эффектом. Для описания кинетики мартенситного превращения используется часто применяемая для TRIP-сталей модель Олсона и Койна [97]. Принимается, что скорость роста объемной доли каждого варианта мартенсита определяется скоростью образования зародышей новой фазы (в единице объема), равной производной по времени от произведения числа возможных мест образования зародышей в аустените на вероятность их активизации. Количество возможных зародышей определяется числом пересечений полос сдвига в исходной фазе; последнее, в свою очередь, определяется по пластическим деформациям в аустените. Вероятность активизации зародыша в отсутствии внешних приложенных напряжений одинакова для всех геометрических мест зародышей и определяется разностью термодинамического потенциала Гиббса («химической свободной энергии») между аустенитом и мартенситом, зависящей от разности температуры начала мартенситного перехода и текущей температуры. При действии напряжений к химической свободной энергии варианта добавляется механическая энергия, определяемая сверткой тензора напряжений и тензора деформации превращения по рассматриваемому варианту. Для описания кинематики мартенситного превращения также принимается мультипликативное разложение градиента места, в котором упругая составляющая описывает упругие искажения и жесткие ротации, неупругая – пластические и трансформационные деформации. Модели, основанные на физических теориях пластичности, в большинстве случаев применяются для анализа областей, представляющих собой отдельное зерно или их совокупность, поскольку для описания реальных процессов с использованием напрямую МКЭ (прямые модели первого типа [51, 52]) в трехмерной постановке требуются существенные вычислительные за28 траты. В этом случае каждое зерно представляется совокупностью конечных элементов, для каждого из которых непосредственно применяется та или иная физическая теория. В прямых моделях первого типа нет явного разделения на масштабные уровни, поэтому с помощью МКЭ проводится моделирование расчетной области с большой дискретизацией. Работа [70] посвящена исследованию мартенситных фазовых превращений с акцентом на стали, обнаруживающие способность к неупругому деформированию в процессе превращений. Термомеханическое поведение сталей моделируется в рамках континуальной механики и микромеханики. В работе получено описание поведения отдельного аустенитного зерна, от которого можно перейти к описанию поведения поликристаллического образца с использованием классических методов связи различных уровней. Микромеханическая модель основана на рассмотрении кинематики, кинетики и термодинамики мартенситного превращения. Пластические деформации родительской и образовавшейся фаз, объемные доли каждого варианта мартенсита выступают в качестве внутренних переменных, описывающих изменение микроструктуры монокристалла. Из соотношений для свободной энергии Гельмгольца и диссипации в рамках термодинамики необратимых процессов получены движущие силы, связанные с внутренними переменными. Двухуровневая модель, пригодная для описания поведения TRIP – сталей, рассматривается в [76]. Для анализа были выбраны уровень представительного макрообъема (макроуровень) и уровень кристаллитов или отдельных фаз (мезоуровень). На макроуровне полные деформации представляются суммой упругой, термической, пластической и трансформационной составляющих. Аналогичное разложение полной деформации принято на мезоуровне для каждой точки представительного объема (ПО) макроуровня. Деформации макроуровня определяются осреднением деформаций с мезоуровня, взвешенных с объемными долями соответствующих фаз. Для определения напряжений в каждой из фаз используется самосогласованная модель [78], где рассматривается поведение заключенного в матрицу с эффективны29 ми свойствами поликристалла, отдельного включения-зерна, имеющего каноническую форму. Предложено эволюционное уравнение для скорости изменения доли мартенситной фазы на мезоуровне, включающее «потенциал превращения», зависящий от эффективных напряжений (разности действующих напряжений и остаточных микронапряжений), деформаций и температуры. Трехуровневая модель для исследования поведения TRIP–сталей и метастабильных аустенитных сталей рассмотрена в статье [83]. Элементом макроуровня является представительный макрообъем, состоящий из множества зерен. Элементом мезоуровня считается зерно, которое изначально является однофазным (аустенит). Каждый элемент мезоуровня подразделяется на совокупность элементов микроуровня, которые представляются подобластью зерна в виде пластинки, состоящей из двух слоев (аустенита и мартенсита) и ориентированной параллельно габитусной плоскости варианта. Полные градиенты места для элемента микроуровня полагаются известными. Напряжения в отдельном элементе микроуровня определяются осреднением по пластине. Напряжения на мезоуровне находятся осреднением напряжений по всем элементам микроуровня. На микроуровне описание кинематики каждой из фаз основано на мультипликативном разложении. Для мартенсита введен сомножитель, описывающий трансформационную составляющую деформации. На межфазной границе принимается условие Адамара для скачка градиента места и равенство векторов напряжений в фазах. Рассматриваются изотермические процессы. Для каждой из фаз вводятся свободная энергия Гельмгольца, зависящая от упругой составляющей градиента места и накопленной пластической деформации, уравнение поверхности текучести и диссипативная функция. Для мартенсита пластическая деформация определяется суммой двух составляющих: накопленной в аустените к моменту превращения и приобретенной в мартенситной фазе. Выражение для движущей силы и критерий фазового перехода получены из неравенства диссипации. Соотно- 30 шения для накопленной пластической деформации получены с помощью принципа максимума диссипации. Двухуровневая модель, предназначенная для анализа связанных термомеханических процессов (включая фазовые превращения, реализуемые диффузионным путем), рассматривается в [89]. На макроуровне используется МКЭ, каждой точке интегрирования в котором приписывается множество кристаллитов (не менее представительного объема (ПО) макроуровня). На мезоуровне применяется вязкопластическая модель, учитывающая скольжение дислокаций и двойникование. Для связи переменных макро- и мезоуровня предлагается использовать либо гипотезу Фойгта, либо самосогласованную схему; напряжения определяются в любом случае осреднением по ПО макроуровня. Фазовые превращения (аустенит – феррит), осуществляемые по диффузионному механизму, описываются с помощью феноменологической модели. Как видно, при построении большинства многоуровневых моделей для описания поведения сталей при термомеханических воздействиях с учетом фазовых превращений мало внимания уделяется вопросу перехода от величин нижнего масштабного уровня к родственным величинам верхнего масштабного уровня, и обычно используются самые простые гипотезы. Широко применяемые самосогласованные модели при решении реальных задач требуют значительных затрат машинного времени. В [65, 66] наряду с мартенситными рассматриваются диффузионные превращения – бейнитные и перлитные. Модель основана на прямом использовании МКЭ. Рассматривается кубическая область, содержащая некоторое количество зародышей новой фазы. Свойства материала в каждом элементе полагаются однородными, соответствующими исходной или получающейся фазе (перлиту, бейниту или мартенситу). Собственно процессы фазовых превращений и критерии их начала не рассматриваются, а полагается, что, начиная с зародышей новой фазы, превращение переходит на следующие слои конечных элементов по предписанной геометрии, испытывая при этом соот31 ветствующие деформации фазового превращения и изменение свойств от исходной фазы к фазе – продукту. Для каждой точки интегрирования применяется теория пластического течения. Для деформации принимается аддитивное разложение на упругую, пластическую и трансформационную составляющие. В работах [32, 33] предложена микромеханическая модель нелинейного деформирования сплавов с эффектом памяти формы при прямом и обратном превращениях. Рассматривается представительный объем поликристаллического материала. Вводится минимальный структурный элемент, который может находиться либо в аустенитном, либо в мартенситном состоянии, – микрообъем. Также вводится мезоэлемент – совокупность микрообъемов, принадлежащих одной мартенситной пластине, т.е. совокупность микрообъемов, примыкающих друг к другу и имеющих одну и ту же ориентацию. Объемная доля мартенситной фазы равна отношению числа микрообъемов, находящихся в мартенситном состоянии, к общему числу микрообъемов (считается постоянным). Увеличение доли мартенсита происходит как за счет развития уже имеющихся мезоскопических мартенситных элементов, так и за счет зарождения новых микрообъемов. Ориентация кристаллографической деформации в первом случае не зависит от действующих напряжений, а идентична ориентации микрообъемов, составляющих мезоэлемент, во втором же случае ориентация кристаллографической деформации определяется действующими в них напряжениями. Процесс обратного превращения сводится к уменьшению до нуля объема мартенситных элементов. Путем подсчета вероятностей различных ориентаций образующихся и переориентирующихся мартенситных элементов были получены соотношения для приращения фазовой деформации представительного объема. Полученные определяющие соотношения позволили качественно правильно описать накопление деформаций прямого превращения, явления ориентированного превращения, монотонной и обратимой памяти формы. 32 В работах [20, 21] предложена динамическая теория мартенситного превращения в сплавах железа. В этих материалах процесс превращения реализуется за счет кооперативной перестройки решетки и происходит со сверхзвуковой скоростью в областях исходного аустенита, что позволяет уйти от моделей подвижности межфазной границы и сосредоточится на волновом управлении процессом роста кристалла мартенсита. Отмечается, что высокая скорость роста требует гетерогенного зарождения, т.е. явного участия дефектов, а волновой характер роста мартенсита требует существования начального колебательного возбужденного состояния решетки в упругом поле дефектов. Именно поэтому не нужно конструирование квазиравновесного зародыша путем обособления некоторой области исходной фазы конфигурированными наборами дислокационных петель. Было установлено, что упругое поле дефекта в области зарождения новой фазы уменьшает энергетический барьер начала плоской деформации с инвариантной плоскостью. В качестве элемента, где через энергетический барьер происходит коллективный переход атомов, берется трехмерная ячейка, имеющая форму прямоугольного параллелепипеда. Грани параллелепипеда попарно колеблются в противофазе, стимулируя деформацию растяжения-сжатия во взаимно ортогональных направлениях, которые совпадают с направлением распространения волн, излучаемых колеблющимся параллелепипедом. При этом решетка теряет устойчивость, и в местах, где налагаются волновые пучки с благоприятным для осуществления деформации полем смещения атомов, образуются области в форме пластинок. Таким образом, формирование пластинок мартенсита рассматривается как перемещение параллелепипеда с некоторой скоростью, определяемой скоростями волновых пучков. В работе изложен алгоритм расчета ориентаций габитусных плоскостей, связанных с распространением управляющего волнового процесса. При аналитическом описании смещений и деформаций решетки в области локализации начального возбужденного состояния используется гармоническая форма. Представлена система волновых уравнений, отражающих взаимодействие двух пучков с ортогональными 33 волновыми векторами. Взаимодействие волн выражается через зависимость коэффициентов затухания от деформаций. Авторами утверждается, что динамическая теория не уступает в точности имеющимся подходам, например при определении кристаллографической ориентации габитусов, макросдвига, межфазных ориентационных соотношений. Из приведенного краткого обзора моделей видно, что проблему построения наиболее полной модели неупругого деформирования сталей с учетом фазовых превращений при различных условиях термического и механического воздействия нельзя назвать полностью решенной. В диссертационной работе предложена двухуровневая модель для описания поведения сталей при термомеханических воздействиях с учетом фазовых превращений, основанная на введение в структуру модели внутренних переменных. 1.3. Построение конститутивных моделей материалов с использованием внутренних переменных Суть данного подхода к построению моделей заключается во введении в структуру определяющих соотношений (ОС) внутренних переменных, под которыми понимаются параметры, описывающие состояние и изменение микроструктуры материала. Внутренние переменные бывают явные ( J e , 1, B e ) и неявные ( J i , 1, B i ), а их полная совокупность определяется как: J J e , J i , 1, B, 1, B e , 1, B i , B B e B i . При этом явные внутренние переменные входят в ОС рассматриваемого масштабного уровня, а неявные – в эволюционные уравнения в качестве параметров. Для связи внутренних переменных двух групп служат замыкающие уравнения. При использовании подхода с явным введением внутренних переменных принимается гипотеза о том, что реакция материала в любой момент времени определяется значениями его термомеханических характеристик, внутренних переменных и параметров воздействия. Рассмотренная гипотеза позволяет отказаться от достаточно сложных ОС в операторной форме, но сохранить 34 свойство памяти материала о предыстории воздействия, носителями которой в данном случае являются эволюционирующие внутренние переменные [46, 47, 107]. Ниже приведена структура конститутивной модели с внутренними переменными, в которую входят ОС, эволюционные и замыкающие уравнения: Σ r Fr P , J e , (1.3.1) J ir R r P , J i , (1.3.2) J er C r P , J i , (1.3.3) где Σ, Σ r – мера напряженного состояния и ее объективная скорость изменения; P , 1, – параметры воздействия, которые могут иметь различную природу; верхний индекс «r» обозначает производную, не зависящую от выбора системы отсчета; F, R, C в самом общем случае являются операторами, которые при построении ОС с использованием внутренних переменных имеют достаточно простой вид и в частном случае могут быть тензорзначными функциями тензорзначных аргументов. Вопрос о выборе вида ОС, эволюционных и замыкающих уравнений в каждом отдельном случае решается исследователем; при этом в рассмотрение принимаются соображения физического характера, сложность записи соотношений, ясность интерпретации полученных результатов и т. д. 35 2. Двухуровневая модель для описания поведения сталей при термомеханических нагружениях с учетом фазовых превращений 2.1. Структура двухуровневой модели Для построения модели фазовых превращений в сталях используется двухуровневый подход. Основной принцип двухуровневого моделирования состоит в том, что процессы деформирования и фазовых превращений в материале рассматриваются как на макроуровне (так делается обычно в МДТТ), так и на более низких уровнях, для которых механизмы деформирования и фазовых превращений вводятся в рассмотрение явно. В данном случае в рассмотрение вводятся следующие масштабные уровни: уровень конструкции (физического тела), уровень представительного макрообъема и мезоуровень. Отметим, что в дальнейшем уровень физического тела будет обозначаться как макро-I, а уровень представительного макрообъема – макро-II. Элементом мезоуровня является кристаллит (отдельное зерно, субзерно), а ПО макроуровня состоит из множества кристаллитов (зерен). Отметим, что к собственно модели материала относятся только макроуровень-II и мезоуровень, в связи с чем рассматриваемая конститутивная модель и отнесена к двухуровневым. Для связи различных уровней в структуру ОС на каждом из масштабных уровней вводятся явные внутренние переменные, определяемые из замыкающих уравнений, описывающих процессы деформирования и фазовых превращений на более глубоких масштабных уровнях по отношению к рассматриваемому. Возможность протекания тех или иных фазовых превращений и их кинетика зависят как от состава стали, так и от параметров термомеханических воздействий на макроуровне, таких как температура, условия нагрева, длительность выдержки, скорость охлаждения, механическая нагрузка и т. п. Как показывают многочисленные экспериментальные исследования, фазовые превращения являются причиной появления в материале определенного набора физических и механических свойств, которые в значительной степени 36 зависят от микроструктуры материала, механизмов ее формирования и изменения. На мезоуровне можно выделить следующие механизмы неупругого деформирования: пластическое деформирование за счет сдвига по кристаллографическим СС; деформирование за счет протекающих в материале фазовых превращений; температурные деформации. Одним из важнейших процессов на мезоуровне, происходящих при фазовых превращениях в сталях, является перераспределение углерода и легирующих элементов, что оказывает значительное влияние на свойства материала (модуль упругих свойств, коэффициент теплопроводности, параметры решетки и т. д.). Задачу описания поведения сталей при термомеханических нагружениях с учетом фазовых превращений можно подразделить на несколько связанных между собой (под)задач, а именно – задачу определения напряженнодеформированного состояния (НДС), задачу теплопроводности, задачу диффузии атомов легирующих элементов (углерода), задачу определения объемных долей всех сосуществующих фаз, т. е. связанная задача «расщепляется» по физическим процессам [16]. Выделение отдельных подзадач значительно облегчает постановку и последующее решение рассматриваемой задачи, а также позволяет использовать для разных подзадач различные типы математических моделей. Учет связанности рассматриваемой задачи приводит к эффектам, описанным ниже. Так, в задаче определения НДС неупругие деформации определяются не только пластической деформацией, но и трансформационной, связанной с происходящими в материале фазовыми превращениями. Помимо этого НДС определяется и температурным режимом за счет введения в ОС температурной деформации. Диффузия легирующих элементов также в значительной степени зависит от градиента температуры. Кроме того, от температуры, концентрации легирующих элементов и фазового состава зависят физико-механические характеристики материала. С другой стороны, в задаче теплопроводности тепловые источники определяются НДС исследуемой области (диссипация энергии за счет происходящих в материале пластических деформаций) и кинетикой фазовых превращений (скрытая теп37 лота фазового превращения). При реализации модели все подзадачи, по сути дела, рассматриваются отдельно и решаются последовательно. Так, при решении задачи диффузии полагаются известным поле температур. При определении объемных долей всех сосуществующих фаз вычисляется значение свободной энергии, зависящей от температуры и концентрации легирующих элементов (углерода), которые найдены из решения задач теплопроводности и диффузии. При рассмотрении задачи определения НДС полагаем известными поле температур и материальных производных от температуры по времени, распределение концентрации легирующих элементов (углерода) и объемные доли всех сосуществующих фаз. На макроуровне I ставится и решается краевая задача в обычном смысле (включающая в свою постановку уравнения равновесия в скоростях, определяющее и кинематическое соотношения, уравнения теплопроводности, необходимые начальные и граничные условия). Для задачи определения НДС используется прямая модель второго типа [49, 51, 52] (рис. 7). Элемент макроуровня - II рассматривается как статистическая выборка соответствующих элементов мезоуровня; параметры воздействий для модели нижнего уровня назначаются с верхнего уровня, а параметры, характеризующие эволюционирующую структуру, текущие физико-механические свойства, неупругие деформации на макроуровне - II, которые далее используются при решении краевой задачи на макроуровне - I, определяются из условия согласования ОС двух масштабных уровней. 38 Рис. 7. Схематическое представление масштабных уровней для задачи определения НДС Для температурной задачи используется прямая модель первого типа [49, 51, 52] (рис. 8). Рис. 8. Схематическое представление масштабных уровней для температурной задачи Для осуществления связи задачи определения НДС с задачей теплопроводности (диффузии) производится геометрическая привязка статистических элементов, используемых при определении НДС, к физическим (пространственным) элементам в температурной задаче, т. е. кристаллиты – элементы мезоуровня в задаче определения НДС привязываются к реальным объектам, 39 имеющим конкретную геометрию. В случае использования прямой модели первого типа каждой макроскопической точке интегрирования (элементу макроуровня - II) приписывается совокупность зерен с заданным распределением ориентаций. Каждый элемент мезоуровня (кристаллит) аппроксимируется совокупностью конечных элементов. С макроуровня - I для каждой точки интегрирования передаются температура и ее градиент. Для построения модели используются две системы координат (СК): условно неподвижная лабораторная система координат (ЛСК) и СК, связанная с решеткой родительской фазы – аустенита. Диффузия в твердых телах является результатом случайных периодических скачков атомов из одного узла решетки в соседний. Эти скачки случайны в том смысле, что движение любого атома не зависит ни от движения других атомов, ни от того, как перед этим двигался он сам. Диффузионные скачки происходят и в отсутствии градиента концентрации, но диффузионный поток при этом не возникает. Рассмотрим основные результаты, следующие из модели случайных блужданий, примененной к описанию диффузии в твердых телах. Первая зависимость сводится к тому, что среднеквадратичное смещение атома после n скачков (за время t) пропорционально n (или t): xn2 2 n 2t 2 t , где – длина скачка (величина постоянная и равная расстоянию до ближайшего соседа); – частота скачков; – среднее время «оседлой» жизни (между двумя скачками). Таким образом, диффузионный путь, который проходит частица за время t, совершая случайные блуждания, xдиф xn2 12 , пропорционален (в среднем) t1 2 . Скорость диффузионного перемещения падает со временем: если xдиф t , то vдиф dxдиф dt t 1 2 . Разумеется приведенная зависимость справедлива только как средняя для большого числа частиц. Для одной час- 40 тицы смещение после n скачков может принимать любые значения между xn min 0 и xn max n . Вторым важным результатом теории случайных блужданий является то, что коэффициент диффузии d связан с характеристиками случайных блужданий следующим соотношением: d 2 / 2 , где – геометрический множитель, зависящий от типа кристаллической решетки. Тогда диффузионный путь xдиф xn2 12 t , а общий путь, прохо- димый атомом за время t определяется соотношением x t . Приведенное соотношение для коэффициента диффузии справедливо, как было подчеркнуто выше, если все направления очередного скачка равновероятны. Если же последовательные скачки связаны между собой и последующий зависит от того, каким был предыдущей, то такая корреляция скачков приводит к уменьшению коэффициента диффузии на фактор корреляции f: d f 2 , где фактор корреляции всегда меньше единицы (0.83 для ГЦК решетки, 0.75 для ОЦК решетки). В литературе [31] говорится о том, что для большинства конструкционных сталей в условиях термомеханического воздействия диффузионный путь атомов легирующих элементов (углерода) за характерное время процесса мал. Оценим диффузионный путь атомов углерода при ферритном фазовом превращении, происходящем в стали с содержанием 0.1 ат.% С-1.43 ат.% Mn и протекающем в течении 500 с. Изначально сталь состоит только из аустенита, размер зерна порядка 200 106 м . Примем, что коэффициент диффузии равен d 2 10 12 м2 [116], длина скачка равна 3А . Параметр для с кубической решетки равен 1 [31], т. к. предполагается, что диффузия проис6 41 ходит равновероятно в трех взаимно перпендикулярных направлениях. Из связи коэффициента диффузии с параметрами случайных блужданий определим частоту скачков 1.331 108 , тогда диффузионный путь атомов углерода за время рассматриваемого процесса составит хдиф 7.74 105 м . Из рассмотренного примера видно, что диффузионный путь при довольно значительном времени процесса мал, поэтому процесс диффузии на больших масштабах можно считать очень медленным, а задачу о перераспределении атомов углерода и легирующих элементов на макроуровне - I не ставить и не решать, а принять на этом уровне гипотезу о заданном распределении концентрации во всем теле. При решении задачи диффузии на макроуровне - II предлагается использовать прямую модель первого типа, когда каждому зерну ставится в соответствии совокупность конечных элементов. Параметры диффузии макроуровня - I получаются осреднением по элементу макроуровня - II. Отметим, что здесь и далее величины макроуровня обозначаются заглавными буквами, а мезоуровня – соответствующими строчными буквами. В МДТТ традиционно используются симметричные меры напряженного и деформированного состояния, и, как правило, их применение должным образом не обосновывается. Так, симметрия тензора напряжений следует из уравнения баланса момента количества движения только в случае отсутствия внутренних моментных напряжений. Однако когда ПО макроуровня ставится в соответствие совокупность произвольно ориентированных элементов мезоуровня (отдельных зерен), использование на мезоуровне симметричных мер напряженного и деформированного состояния представляется не вполне обоснованным, например, из-за определенных симметрийных свойств решетки или некоторых особенностей построения физических теорий пла- стичности, используемых для описания неупругого поведения материала. Так, при проведении экспериментов по определению значений независимых компонент тензора упругих свойств на макроуровне для различных монокристаллов полагается симметрия мер напряженного и деформированного со42 стояния, что предопределяет симметрию тензора упругих свойств внутри первой и второй пар индексов. В соотношения большинства известных физических теорий пластичности входит явным образом симметризованный ориентационный тензор систем скольжения (СС) кристаллита. При этом между физическим смыслом этой величины и соотношением, которым она определяется, возникает несоответствие; например, для кристаллитов с любой решеткой симметризацией ориентационного тензора наряду с реально существующей СС (h k l) [p q r] «вносится» еще одна СС (p q r) [h k l], ни теоретически, ни экспериментально не проявляющая свойств действительной СС [5]. При построении модели на мезоуровне встает вопрос о выборе несимметричной меры скорости деформации. В качестве меры скорости деформации необходимо выбрать меру относительного смещения материальных частиц, исключив при этом любое движение среды как жесткого целого. В качестве меры скорости изменения деформированного состояния предлагается использовать градиент скорости относительного движения частиц: v r v ω , v – скорость перемещений; ω – спин решетки (кристаллографической СК). В статье [50] показано, что введенная таким образом мера деформированного состояния является индифферентной, т. е. не зависит от выбора системы отсчета. В физических теориях в качестве меры деформации удобней использовать транспонированный градиент относительной скорости v Tr vT ω , который также не зависит от выбора системы отсчета. Следует отметить, что введенное определение скорости изменения деформированного состояния согласуется с использованием в качестве ОС закона Гука в скоростной релаксационной форме, записанного с позиции наблюдателя в КСК, связанной с решеткой аустенита: компоненты тензора упругих свойств «привязаны» к решетке, в качестве меры скорости изменения напряженного состояния принята «решеточная» коротационная производная тензора напряжений Коши. При переходе на макроуровень осуществляется симметризация меры напряжений, что связано с отсутствием физических причин появления мо43 ментных взаимодействий (распределенных поверхностных и массовых моментов) на данном уровне. В силу симметрии тензора напряжений тензор упругих свойств должен быть симметричным по индексам первой пары. Тогда из существования упругого потенциала (из чего вытекает симметрия по парам индексов) следует симметрия тензора упругих свойств и по второй паре индексов. Таким образом, в рассматриваемом разделе приведена общая структура двухуровневой модели. Для облегчения постановки и последующего решения связанная задача разбивалась на отдельные подзадачи, что позволило для разных подзадач использовать различные типы моделей. Для каждой из подзадач сформулированы основные гипотезы, приводятся содержательная и концептуальная постановки. Также осуществлялся выбор несимметричных мер скорости деформации (градиент относительной скорости перемещений) и напряжений (тензор напряжений Коши). 2.2. Математическая постановка задачи 2.2.1. Постановка задачи на макроуровне I На макроуровне - I необходимо определить скорости перемещений, напряжения, деформации и распределение температуры, удовлетворяющие следующей системе уравнений [36]: уравнению равновесия в скоростях ˆ Σ ˆ V : ˆ Σ B 0 ; (2.2.1) определяющему соотношению Σ CR Σ Σ Ω ΩT Σ П : Z r Zinr Zthr ; (2.2.2) кинематическим соотношениям Z r Z Ω, Z Vˆ ; (2.2.3) уравнению теплопроводности ˆ Λ ˆ Y ; (2.2.4) 44 граничным условиям V VГ на Г V ; (2.2.5) ˆ V N Σ N ˆ V N N Σ T на Г ; N Σ Σ (2.2.6) Г на Г ; (2.2.7) N Λ ˆ N G h (2.2.8) N Λ ˆ N G G на Г G ; на Г Г ГG , (2.2.9) при начальных условиях V t 0 V0 , (2.2.10) ˆ Σ B 0, 0 0 (2.2.11) N Σ 0 T0 , (2.2.12) t 0 0 . (2.2.13) В соотношениях (2.2.1) – (2.2.3) Σ – тензор напряжений Коши макроуровня; B – вектор распределенных объемных сил; V – вектор скорости перемещения; П — тензор упругих свойств; Z r , Zinr – транспонированный градиент относительной скорости перемещений, его неупругая составляющая; Z thr – термическая составляющая транспонированного градиента относительной скорости перемещений; Ω — тензор спина макроуровня; верхний индекс «СR» обозначает коротационную производную. Вся поверхность тела Г разделена на две части – Г Σ и Г V . На Г Σ задаются силовые граничные условия, а на Г V – кинематические. Следует сразу же отметить, что зависимости тензора термического расширения, теплоемкости, тензора теплопроводности и тензора упругих свойств отдельных зерен от температуры определяются экспериментально и имеют весьма сложный вид, причем характер этих зависимостей может отличаться для различных марок сталей. Поэтому вид зависимостей физико-механических свойств материала от температуры должен обсуждаться отдельно для каждой конкретной задачи. Для многофазных систем эти параметры зависят от фазового состава и определяются по правилу 45 смеси. В (2.2.5) – (2.2.6) и (2.2.10) – (2.2.12) VГ – значение скорости перемещения на части границы Г V ; N – вектор внешней нормали к поверхности; T – вектор поверхностных сил; нижний индекс «0» указывает на значения величин в начальный момент времени. В уравнениях, описывающих температурные поля (2.2.4), (2.2.7) – (2.2.9), (2.2.13), , 0 , Г – температура, ее значение в начальный момент времени и на границе; – теплоемкость; Y – мощность внутреннего теплового источника; Λ – тензор теплопроводности; Г – часть границы, на которой задается температура; Г G – часть границы, на которой задается проекция вектора теплового потока G Λ на внешнюю нормаль, G ; Г \ Г Г G – часть границы, на которой задается условие теплообмена с окружающей средой по закону Ньютона, h – коэффициент теплообмена, – температура окружающей среды. Тензор упругих свойств П , тензор спина Ω , неупругая составляющая транспонированного градиента относительной скорости перемещений Zinr , термическая составляющая градиента относительной скорости перемещений Zthr , теплоемкость , мощность внутреннего теплового источника Y и тензор теплопроводности Λ в каждой точке интегрирования определяются из моделей для ПО макроуровня - II, о которых будет говориться ниже. 2.2.2. Определение напряженно-деформированного состояния. Постановка задачи на макроуровне -II На макроуровне -II рассматривается ПО материала, состоящего из совокупности кристаллитов – элементов мезоуровня. Описание процесса деформирования на мезоуровне при использовании прямой модели второго типа осуществляется с помощью статистической модели, т. е. модели, основанной на рассмотрении элементов мезоуровня независимо друг от друга. Элементы мезоуровня объединяются в представительный макрообъем по ряду характеристик на основании гипотез, принимаемых априори. Именно поэтому на макроуровне -II для задачи определения НДС нет необходимости в по46 становке и решении краевой задачи. Конститутивная модель материала на рассматриваемом уровне включает следующую систему уравнений: Σ CR Σ Σ Ω ΩT Σ П : Z r Zinr Zthr , (2.2.14) П П п , o , i 1..M , Z Z ζ , п , ω , i 1..M , Z Z ζ , п , i 1..M , (2.2.15) Ω Ω ωi , п i , i 1..M , i i in r in r in r i i th r th r th r i i i (2.2.16) (2.2.17) (2.2.18) где M – число элементов мезоуровня, необходимых для описания ПО макроуровня; i – индекс номера элемента мезоуровня (далее опускается). На макроуровне явными внутренними переменными [47] являются неупругая составляющая градиента относительной скорости перемещений Zinr , термическая составляющая градиента относительной скорости перемещений Zthr , тензор спина Ω , тензор упругих свойств П . В качестве неявных внутренних переменных, входящих в замыкающие уравнения (2.2.15) – (2.2.18), используются неупругая составляющая градиента относительной скорости перемещений ζinr , термическая составляющая градиента относительной скорости перемещений ζthr , тензор спина ω , тензор упругих свойств п отдельных кристаллитов. Роль эволюционных уравнений, в которые вышеперечисленные характеристики кристаллитов входят в качестве переменных, играют соотношения модели мезоуровня. 2.2.3. Определение напряженно-деформированного состояния и фазового состава. Постановка задачи на мезоуровне Закон Гука в скоростной релаксационной форме используется в качестве определяющего соотношения на мезоуровне (индексы номеров элементов мезоуровня для упрощения записи опущены): σ cr σ ω σ σ ω п : ζ r ζ inr ζ thr , (2.2.19) 47 где σ, σcr – тензор напряжений Коши и его коротационная производная; ˆ ω v ˆ – транспонированный градиент относительной скороζ r ζ ω v r сти перемещений (индексом r обозначены величины, характеризующие относительное движение, фиксируемое подвижным наблюдателем в жесткой подвижной системе отсчета мезоуровня); v – скорость перемещений. В начальный момент времени все зерна однофазны (аустенит). При фазовых превращениях в каждом зерне аустенит может полностью или частично перейти в новую фазу, т. е. зерна становятся многофазными. Под фазой в гетерогенной системе будем понимать некоторую область, которая «отделена» от других физически существующей поверхностью – межфазной границей. Каждая фаза имеет определенную микроструктуру и гомогенные свойства, отличные от свойств в других областях системы. При изучении их можно различать, например, по составу, кристаллической структуре и т.п. Функция состояния (термодинамический потенциал) гетерогенной системы в значительной степени зависит от фазового состава, поэтому каждую фазу можно рассматривать как область, которая в равновесном состоянии имеет вполне определенный термодинамический потенциал, отличный от потенциала других фаз. При определении параметров многофазной системы гетерогенная многофазная среда заменяется эквивалентной гомогенной, где эффективные свойства определяются осреднением локально неоднородных свойств в каж1 m дой фазе: x xk dv . Полагается, что градиент скорости перемещений v k 1 vk одинаков во всех фазах, т.е. применяется (расширенная) гипотеза Фойгта. Для неупругой составляющей градиента относительной скорости перемещения и для всех свойств материала (тензор упругих свойств, тензор термического расширения, тензор теплопроводности, коэффициент теплоемкости) принимается правило смеси, которое вытекает из пространственного осреднения, используемое в обычной схеме гомогенизации. 48 Неупругая составляющая градиента относительной скорости перемещений определяется двумя составляющими: пластической и трансформационной: n m1 m 2 ζ i Pi i ifi* ; in r i k k k 1 (2.2.20) i термическая составляющая градиента относительной скорости перемещения записывается в виде: ζthr α , где i vi v (2.2.21) – объемная доля соответствующей фазы ( v i – объем, занимае- мый i-ой фазой, v – объем области, занимаемый отдельным зерном); fi* – градиент трансформационной деформации, описывающий превращение начальной фазы в i-ую; m1 – количество фаз, испытывающих пластическую деформацию; m2 – количество фаз, которые могут образоваться в процессе фазового превращения (следует отметить, что различные варианты мартенсита, образующиеся при бездиффузионном превращении, рассматриваются как отдельные фазы, т. к. они имеют вполне определенные термодинамические потенциалы, отличные друг от друга); Pi b i n i – ориентационный тензор kk k k й СС; ni k – единичный вектор нормали к плоскости скольжения; bi k – еди- ничный вектор по направлению вектора Бюргерса, характеризующий наk правление скольжения; i – скорость сдвига по k-й СС i-й фазы (принято удвоенное количество СС, т. е. СС с положительным и отрицательным направлениями сдвига считаются различными); α – тензор термического расширения. Определение тензора упругих свойств и тензора термического расширения в многофазной системе осуществляется по правилу смеси: m п i пi , (2.2.22) i 1 49 m α iα i , (2.2.23) i 1 где m – количество сосуществующих в многофазном зерне фаз; пi , α i – значения соответствующих величин в i-й фазе. Необходимо отметить, что тензоры пi являются симметричными по парам индексов пijkl пklij , но в общем случае не являются симметричными внутри пар индексов: пijkl п jikl , пijlk пijkl . На мезоуровне явными внутренними переменными являются неупругая составляющая градиента относительной скорости перемещений ζ inr , термическая составляющая градиента относительной скорости перемещений ζ thr , тензор спина ω , тензор упругих свойств п . В качестве неявных внутренних k переменных выступают скорости сдвига по СС i , сопротивления сдвигу ci k , ориентационные тензоры o , объемные доли сосуществующих в зерне фаз i и скорости их изменения i , для которых записываются эволюционные уравнения. Соотношение (2.2.20) играет роль замыкающего уравнения, связывающего пластическую составляющую относительной скорости перемещений элемента мезоуровня со скоростями сдвигов по СС в рамках данного зерна, и трансформационную составляющую – со скоростями изменения объемных долей фаз. Соотношение (2.2.21) также играет роль замыкающего уравнения, связывающего термическую составляющую относительной скорости перемещений элемента мезоуровня со скоростью изменения температуры в рамках данного элемента. К группе замыкающих уравнений, кроме того, относятся соотношения для определения тензора упругих свойств в многофазной системе, спина решетки. Для определения скорости сдвига по СС при пластическом деформировании используется закон следующего вида: i k 0 ki H i k ci k i k k ci 1 mci , (2.2.24) 50 k k где ci – критическое напряжение сдвига по k-й СС; 0 i – материальный па- раметр; mci – параметр скоростной чувствительности; i Pi : σ – сдвигоk k вое напряжение, действующее в k-й СС i-й фазы. Наибольшее влияние изме нение температуры оказывает на критическое напряжение сдвига ci , котоk рое будет учтено за счет введения в закон упрочнения явной зависимости от температуры. Сопротивление сдвигу ci в каждый момент процесса определяется k следующими соотношениями: ci k i mi n j ci k ˆci Qi j k k k i i ci 0 Bi ci 0 a ji exp n k j 1 j R ci 0 i j 1 , i 1, i j 0, (2.2.25) ci k 0 ci k0 , где ci 0 – начальный предел текучести в k-й СС при отсчетном значении темk пературы, которое для каждого рассматриваемого процесса выбирается индивидуально (например, для TRIP сталей процессы бездиффузионных фазовых превращений и пластического деформирования начинают протекать при комнатной температуре в условиях только механического воздействия, поэтому все начальные значения параметров определяются при комнатной температуре; диффузионные превращения происходят при достаточно высоких температурах, поэтому в данном случае все начальные параметры определяются при температуре начала рассматриваемого процесса); mi ,ˆci – материальные константы; Bi – параметр, характеризующий скорость релаксации; Qi – энергия активации движения дислокаций; a ji – параметры упрочнения, коk торые обычно разделяют на параметры деформационного (i=j) и латентного t j (i≠j) упрочнения; i j – накопленный сдвиг по СС j, i i d . Параметр j 0 51 деформационного упрочнения отвечает за влияние предшествующей деформации по СС на критическое напряжение в этой же системе. Параметр латентного упрочнения отвечает за влияние на критическое напряжение в рассматриваемой СС дислокационных процессов, происходящих в других системах. К упрочнению могут приводить различные физические причины, и в первую очередь это взаимодействие дислокаций друг с другом или дислокационными структурами. Учет рассмотренных выше реакций, приводит к нелинейному упрочнению, поэтому используется степенной закон. Под знак суммы в (2.2.25) введен не накопленный в СС сдвиг, а отношение накопленного в данной системе сдвига к суммарному накопленному сдвигу. Это делается для учета меры сложности предыдущего деформирования (например, уменьшения плотности мобильных дислокаций в процессе деформирования). Этот множитель при одиночном скольжении всегда равен единице, т. е. скорость упрочнения пропорциональна скорости сдвига, но дополнительной зависимости критических напряжений от накопленных сдвигов и от сложности нагружения на мезоуровне не будет. Этот множитель будет стремится к нулю (и при увеличении показателя степени все больше) при увеличении числа различных СС, участвующих в процессе скольжения. Второе слагаемое в законе упрочнения описывает влияние температуры на критическое напряжение сдвигу. Считается, что в сталях с ростом температуры происходит разупрочнение, поэтому вклад второго слагаемого в упрочнение отрицательный. При низких температурах значение этого слагаемого пренебрежимо мало по сравнению с первым. С ростом температуры величина второго слагаемого может превысить величину первого, что приведет к отрицательному приращению и, следовательно, уменьшению сопротивления сдвигу. Стоит отметить, что с постепенным увеличением температуры процесс разупрочнения материала идет более интенсивно. Однако критическое напряжение сдвигу не может изменяться бесконечно, а стремится к некоторой величине ˆci . Для некоторых типов сталей при бейнитном и мартенситном превращениях наблюдается значительное влияние изменения объемной доли новой 52 фазы на развитие пластической деформации в родительской фазе (остаточном аустените), т. к. образование новой фазы может стать причиной появления препятствий для скольжения дислокаций и значительно изменить локальное поле напряжений. Из экспериментов известно, что по мере развития фазового превращения сопротивление сдвигу в аустените значительно возрастает. В данном случае сопротивление сдвигу (обозначим его через c A ) k будет зависеть не только от пластической деформации, но и от изменения объемной доли новой фазы [67]. Этот факт в модели можно учесть добавлением к закону упрочнения дополнительного слагаемого (считается, что наличие новой фазы приводит к одинаковому изменению сопротивления сдвигу во всех СС): k cA A mA n j k cA ˆcA QA j k k k A A cA0 BA cA0 a jA n exp k j 1 j R cA 0 A j 1 m2 (2.2.26) H ii , i 1 A 1, j A 0, k cA 0 cAk 0 , где H i характеризует скорость упрочнения аустенита из-за увеличения объемной доли новой фазы; т2 – количество фаз, которые могут образоваться при фазовом превращении (например, различные варианты мартенсита, которые будут оказывать влияние на сопротивление сдвигу в аустените). Пластическая деформация аустенита может оказывать значительное влияние на процесс фазовых превращений. Степень этого влияния зависит от температуры и степени деформации. При умеренной пластической деформации аустенита (до 8%) возникают такие структурные нарушения и локальные напряжения, которые в большинстве случаев активизируют фазовые превращения, что проявляется в повышении температуры начала превращения, увеличении скорости превращения и уменьшению доли непревращенной фазы 53 [31]. Значительная (до 30%) пластическая деформация оказывает тормозящее действие на переход. Например, мартенсит возникает под воздействием пластических сдвигов, подготовленных пластической деформацией, в которых его зарождение облегчено; при больших деформациях, когда плотность дислокаций высока, затрудняются сдвиговые процессы, контролирующие образование кристаллов мартенсита и их рост [43]. Значительное влияние пластической деформации аустенита на упрочнение в новой фазе экспериментально установлено для бейнита и мартенсита (однако следует отметить, что пластической деформацией мартенсита в большинстве случаев пренебрегают). В данном случае образующаяся фаза наследует дислокационную структуру родительского аустенита [70]. Для учета данного механизма в закон упрочнения вводится дополнительное слагаемое, описывающее упрочнение новой фазы на системе скольжения k, связанное с предшествующей пластической деформацией аустенита: ci k i mi n j ci k ˆci Qi j k k k i i ci 0 Bi ci 0 a ji exp n k j 1 j R ci 0 i j 1 i l k cA k ci 0 (2.2.27) , i 1, i j 0, ci k 0 ci k0 , где cA l k – критическое напряжение сдвига аустенита по l-й СС на момент начала превращения, которая в процессе превращения переходит в СС k но- вой i-й фазы; cA ci 0 max 0, ( cA ci 0 ) . l k k l k k Изменение ориентации зерна определяется по его спину в результате интегрирования соотношения: ω o o T . (2.2.28) В данной работе все изменения ориентаций зерен связываются с происходящими в аустените и феррите пластическими деформациями, потому 54 что в большинстве случаев при изучении фазовых превращений пластическими деформациями и разворотами решетки, которые могут происходить в образующейся твердой фазе (мартенсите), можно пренебречь. Спин определяется поворотом решетки вместе с материалом зерна при наложенном кинематическом воздействии и описывается с использованием модели поворота Тейлора [104]: 1 m1 n k k k k k ω w i i bi ni ni bi , 2 i1 k 1 * где w * (2.2.29) 1 1 v v ζ ξT . 2 2 Экспериментально установлено, что для металлов в поворотах решетки несовместность скольжения дислокаций в соседних зернах играет существенную роль [39], поэтому модель для описания поворотов решетки можно усложнить за счет введения дополнительной составляющей, характеризующей ротацию собственно решетки кристаллита, обусловленную взаимодействием с окружением, для описания которого вводится внутренняя переменная – действующее на зерно моментное напряжение [54]. Изменение объемной доли описывается следующим кинетическим соотношением: m 1 f 1 f i lij t j j 1 i , (2.2.30) где f – свободная энергия Гиббса, lij – кинетические коэффициенты, – температура. Вывод кинетического соотношения (2.2.30) рассматривается в параграфе 3.1. 2.2.4. Постановка задачи теплопроводности для представительного макрообъема После определения объемных долей всех сосуществующих фаз в отдельном зерне с использованием соотношений (2.2.30), можно по правилу 55 смеси определить тензор теплопроводности и коэффициент теплоемкости в каждом зерне: m λ i λ i , (2.2.31) i 1 m i i , (2.2.32) i 1 где λ i , i – значения соответствующих величин в i-й фазе. Мощность внутреннего теплового источника в зерне определяется как: m1 n i 1 k 1 m2 y i i i i gii , k k (2.2.33) i 1 где g i – скрытая теплота фазового перехода, i – плотность. Краевая задача для уравнения теплопроводности ставится и решается для ПО макроуровня, т. е. для элемента макроуровня – II. В свою очередь элемент макроуровня – II представляет собой совокупность элементов мезоуровня – отдельных зерен с определенной ориентацией кристаллографической системы координат (КСК) относительно лабораторной системы координат (ЛСК). Каждому зерну ставится в соответствии совокупность конечных элементов, поэтому краевая задача для элемента макроуровня – II ставится в терминах переменных мезоуровня. При решении задачи теплоемкость, тензор теплопроводности и мощность внутреннего теплового источника для конечных элементов, покрывающих элемент мезоуровня, берутся одинаковыми. После решения краевой задачи получаем значение температуры во всех узлах конечно-элементной сетки. Температура в конечном элементе определяется средним арифметическим температур в узлах элемента. Температура в элементе мезоуровня (зерне) находится осреднением по всем элементам, аппроксимирующим зерно. Запишем уравнение теплопроводности: λ y , (2.2.34) – теплоемкость, λ – тензор теплопроводности, y – мощность внутреннего источника тепла. Особенности записи граничных и начальных условий для задачи макроуровня – II обсуждаются в п.2.3.2. 56 2.2.5. Постановка задачи диффузии для представительного макрообъема Для описания перераспределения углерода и легирующих элементов, которое играет важную роль в процессах фазовых превращений при термомеханических воздействиях, для области, представляющей собой совокупность элементов мезоуровня, ставится и решается краевая задача: cip d ip cip cipd pi , (2.2.35) cip t 0 cip0 , (2.2.36) cip ciГp на Г с , (2.2.37) где cip , cip0 , ciГp – концентрация p-го легирующего элемента, ее значение в начальный момент времени и на границе для i-й фазы; d ip , d pi – тензоры диффузии и термодиффузии p-го компонента в i-й фазе; на границе Г с поддерживается заданное распределение вещества. После решения краевой задачи получаем значение концентрации во всех узлах конечно-элементной сетки. Концентрация в конечном элементе определяется средним арифметическим концентраций в узлах элемента. Концентрация в элементе мезоуровня (зерне) находим осреднением по всем элементам, аппроксимирующим зерно. Таким образом, в разделе 2.2 приведены математические постановки на каждом из рассматриваемых масштабных уровней для каждой из подзадач, а именно: задачи определения НДС, температурной задачи, задачи диффузии и задачи определения фазового состава. 57 2.3. Согласование соотношений моделей различных масштабных уровней 2.3.1. Согласование для задачи определения напряженно- деформированного состояния При построении многоуровневых моделей с использованием внутренних переменных одной из важных задач является установление связи однотипных характеристик различных масштабных уровней. В работе [54] предложен подход, который позволяет на верхнем масштабном уровне определить замыкающие уравнения и производную, не зависящую от выбора системы отсчета, с помощью процедуры согласования ОС различных масштабных уровней. При использовании многоуровневого подхода ПО на некотором масштабном уровне ставится в соответствие неоднородная область на более низком масштабном уровне. Аналогично – для последующих масштабных уровней. Поэтому при изложении подхода для согласования ОС можно оперировать двумя уровнями, которые будем называть верхним и нижним. При этом в зависимости от структуры исследуемого материала и особенностей процессов деформирования на каждом из масштабных уровней могут использоваться либо соотношения несимметричной теории (при появлении моментных напряжений), либо осуществляться симметризация мер напряженного и деформированного состояния (при отсутствии причин появления моментных взаимодействий). Далее речь пойдет о случае, когда на верхнем масштабном уровне тензор напряжений является симметричным. ОС верхнего уровня записывается в форме: Σ Ω ΩT Σ П : Z Z in Zth , Σ CR Σ r r r (2.3.1) нижнего уровня (для каждого элемента из выборки, соответствующей ПО верхнего уровня) – в виде: σ cr σ ω σ σ ω п : ζ ζ inr ω ζthr . (2.3.2) Представим величины, входящие в описание НДС нижнего уровня, суммой средних величин по ПО верхнего уровня и отклонением от этих средних: п < п > п / , σ < σ > σ / , ζ < ζ > ζ / , ζ inr < ζinr > ζ inr / , (2.3.3) ω < ω > ω / , ζ thr < ζ thr > ζthr , – оператор осреднения, обладающий свойством: < п / > 0, < σ / > 0, < ζ / > 0, < ζ inr / > 0, < ω / > 0,< ζthr / > 0. (2.3.4) Подставляя (2.3.3) в ОС нижнего уровня (2.3.2), получаем соотношение < σ > σ / < ω > ω / < σ > σ / < σ > σ / < ω > ω / < п > п / : < ζ > ζ / < ζ inr > ζ inr / < ζ thr > ζthr / < ω > ω / . (2.3.5) Осредняя (2.3.5), имеем: < σ > < п >: < ζ > < ζinr > < ζ thr > < ω > < п/ : ζ / ζinr / ζthr / ω / > (2.3.6) < σ > < ω > < σ / ω/ > < ω > < σ > < ω / σ / > . Для согласования ОС (2.3.6) и (2.3.1) необходимо симметризовать ОС нижнего S масштабного уровня). Введем тензор четвертого ранга 1 С II C III ( СII , CIII – изотропные тензоры четвертого ранга [30]), кото2 рый на произвольный тензор второго ранга T действует следующим образом: S:T 1 T TT Ts . 2 Для симметризации ОС (2.3.6) умножим его левую и правую части на S : S :< σ > S : п : < ζ > ζinr ζ rth < ω > п / : (ζ / ζ r in / ζ r th / ω / ) (2.3.7) S : < ω > < σ > < σ > < ω > S : ω / σ / σ / ω / . Так как напряжения на верхнем масштабном уровне определяются как осредненные симметризованные напряжения нижнего масштабного уровня 59 Σ S :< σ >, (2.3.8) то соотношение (2.3.7) с учетом (расширенной) гипотезы Фойгта Z ζ, ζ / 0 (2.3.9) запишется в виде: Σ S п : < ζ > < ζ r in > < ζ r th > < ω > п / : (ζ r in / ζ r th / ω / ) (2.3.10) S < ω > < σ > < σ > < ω > S ω / σ / σ / ω / , Σ S п : (< ζ > < ζ r in > < ζ r th > < ω >) S п / : (ζ r in / ζ r th / ω / ) (2.3.11) S < ω > < σ > < σ > < ω > S ω / σ / σ / ω / . Третий член в правой части (2.3.11) может быть преобразован следующим образом (вывод соотношения осуществлен Е. С.Макаревич): S : < ω > < σ > < σ > < ω > S : < ω > < σ > S : < σ > < ω > (2.3.12) < ω > S :< σ > S :< σ > < ω >=< ω > Σ Σ < ω > . Покажем справедливость равенства, приведенного выше, для общего случая произвольной СК. Для этого запишем соотношение S : < ω > < σ > < σ > < ω > < ω > S :< σ > S :< σ > < ω > (2.3.13) в компонентах в базисе произвольной СК. Отдельно рассмотрим слагаемые левой и правой частей (2.3.13): 60 S : < ω > < σ > 1 eie jeie j eie je j ei : < > kl e k el < > mn e me n 2 1 eie jeie j eie je j ei : < > kl < > mn lme k e n 2 1 eie jeie j eie je j ei : < > km < > mn e k e n 2 1 < > km < > mn eie j g in g jk < > km < > mn eie j ki g jn 2 1 < > km < > mn eie k g in < > km < > mn e k e j g jn 2 1 < > km < > mn ene k < > km < > mn e k e n . 2 Обратный переход к тензорному представлению приводит к соотношению: S : < ω > < σ > 1 1 < σ >T < ω > T < ω > < σ > . 2 2 (2.3.14) Для второго слагаемого левой части (2.3.13) при использовании произвольного базиса получим: S : < σ > < ω > 1 eie jeie j eie je j ei : < > mn e me n < > kl e k el 2 1 eie jeie j eie je j ei : < > mn < > kl e mel kn 2 1 eie jeie j eie je j ei : < > mn < > nl e mel 2 1 < > mn < > nl eie j li jm < > mn < > nl eie j l j g im 2 1 < > mn < > nl el e m < > mn < > nl eiel g im 2 1 < > mn < > nl el e m < > mn < > nl e mel . 2 При переходе к тензорному представлению последнее соотношение приводится к виду: S : < σ > < ω > 1 1 < ω >T < σ > T < σ > < ω > . 2 2 (2.3.15) Аналогичным образом преобразованию подлежит правая часть соотношения (2.3.13), начиная с первого слагаемого: 61 1 < ω > S :< σ > < > kl e k el eie jeie j eie j e jei :< > mn e me n 2 1 < > kl e k el < > mn eie j g in jm < > mn eie j g jn g im 2 1 < > kl e k el < > mn eie m g in < > mn eie n g im 2 1 < > kl e k el < > mn ene m < > mn e me n 2 1 < > kl < > mn e k lnem < > kl < > mn e k lme n 2 1 < > kn < > mn e k e m < > km < > mn e k e n 2 1 < > kn < > mn e k e m < > kn < > nm ek em . 2 Откуда, возвращаясь к тензорному представлению, получено соотношение < ω > S :< σ > 1 1 < ω > < σ >T < ω > < σ > . 2 2 (2.3.16) Аналогично в произвольном базисе преобразуется второе слагаемое правой части (2.3.13): 1 eie jeie j eie je jei :< > mn emen < > kl ek el 2 S :< σ > < ω >= 1 < 2 1 < 2 1 < 2 1 < 2 1 < 2 1 < 2 > mn eie j g in jm < > mn eie j g jn g im < > kl e k el > mn eie m g in < > mn e me j g jn < > kl e k el > mn ene m < > mn e me n < > kl ek el > mn < > kl e n kmel < > mn < > kl e m knel > mn < > ml enel < > mn < > nl emel > mn < > ml enel < > nm < > ml e nel . для которого переход к тензорному представлению приводит к соотношению: 62 S :< σ > < ω >= 1 1 < σ >T < ω > + < σ > < ω > . 2 2 (2.3.17) Подстановка соотношений (2.3.14) – (2.3.17) в (2.3.13) с одновременным сокращением в левой и правой частях на коэффициент 1 2 приводит к равенству: < σ > T < ω > T < ω > < σ > < ω > T < σ > T < σ > < ω >= =< ω > < σ > T < ω > < σ > < σ > T < ω > < σ > < ω >, откуда < σ > T < ω > T < ω > T < σ > T =< ω > < σ > T < σ > T < ω > . (2.3.18) Тензор < ω > – антисимметричен, следовательно, для него справедливо < ω >T < ω > . Отсюда равенство (2.3.18) преобразуется к виду < σ > T < ω > + < ω > < σ > T =< ω > < σ > T < σ > T < ω >, откуда видно, что исходное равенство (2.3.13) справедливо. В качестве априори принимаемых замыкающих уравнений для тензора упругих свойств, градиента скорости перемещений и тензора напряжений используются следующие: П S:п , (2.3.19) Z ζ , (2.3.20) Σ S :< σ > . (2.3.21) Соотношение для спина получается в результате согласования с ОС верхнего масштабного уровня: Ω ω . (2.3.22) Применение соотношений (2.3.19) – (2.3.22) к осредненному ОС нижнего масштабного уровня (2.3.6) с учетом симметризации приводит к выражению: Σ П : (Z < ζ r in > < ζ r th > Ω) S п / : (ζ r in / ζ r th / ω / ) Ω Σ Σ Ω S ω / σ / σ / ω / . (2.3.23) 63 При сопоставлении выражений (2.3.1) и (2.3.23) получаем соотношения для определения неупругой и термической составляющих градиента относительной скорости перемещений на верхнем масштабном уровне: Z inr < ζ r in > + П 1 : S п/ : (ζ r in / ω / ) (2.3.24) Z thr < ζ r th > + П 1 : S п/ : ζr th / . (2.3.25) П 1 : S ω / σ / σ / ω / , С учетом (2.3.12) соотношение (2.3.24) может быть преобразовано к следующему виду: Z inr < ζ r in > + П 1 : S п/ : (ζ r in / ω / ) П 1 : ω / σ s / σ s / ω / , (2.3.26) 1 / σ σ /T . 2 В данной работе используется простейший вариант осреднения – осред- где σ s / S σ / нение по объему, т. к. рассмотрение вопроса о способе осреднения выходит за рамки исследования и поэтому не обсуждается. Однако нужно отметить, что для некоторых материалов (например, композиционных) вопрос о выборе способа осреднения при определении эффективных характеристик среды в процессе перехода между различными масштабными уровнями является ключевым. 2.3.2. Согласование для задачи теплопроводности Значения температуры и ее градиента определяются суммами средних по объему элемента макроуровня – II величинами и некоторыми флуктуациями [98]: < > / , (2.3.27) / < > , (2.3.28) где оператор осреднения < > обладает следующим свойством: / < > 0 . (2.3.29) 64 Принимается, что средние значения равны значениям температуры и ее градиента в точке интегрирования макроуровня – I: < > , (2.3.30) < > , (2.3.31) поэтому задача теплопроводности сводится к задаче, записанной в терминах флуктуаций. Считается, что в начальный момент флуктуации отсутствуют. Если воспользоваться простейшим способом осреднения – осреднением по объему, то условие (2.3.29) можно записать в следующем виде: / / dV ndГ 0 . V (2.3.32) Г Поэтому при решении краевой задачи граничные условия выбираются таким образом, чтобы последнее равенство выполнялось. В данной работе используются периодические граничные условия: Г/ Г/ Г Г x Г x Г . (2.3.33) где знаки «+» и «–» соответствуют противоположным границам. В качестве представительного макрообъема поликристалла обычно выступает конгломерат, содержащий не менее семи зерен по стороне куба. При решении задачи теплопроводности рассчитываются значения тензора теплопроводности и теплоемкости, которые зависят от фазового состава в рассматриваемом зерне. Также определяется диссипация энергии, связанная с происходящими фазовыми превращениями и пластической деформацией. Примем, что данные величины в каждой точке интегрирования физического тела в точности равны значениям, полученным осреднением по объему рассматриваемой области, т. е. выполняются следующие соотношения: < > , (2.3.34) Λ < λ > , (2.3.35) Y < y > . (2.3.36) Таким образом, рассмотрен вопрос согласования соотношений моделей различных масштабных уровней для задачи определения НДС и температур65 ной задачи. При переходе на макроуровень в задаче определения НДС осуществлялась симметризация меры напряженного состояния, что связано с отсутствием физических причин появления моментных напряжений на данном уровне. Связь параметров различных масштабных уровней в температурной задаче определяет особенности записи граничных и начальных условий краевой задачи для представительного макрообъема. 66 3. Кинетическое уравнение для определения объемных долей сосуществующих фаз 3.1. Вывод кинетического уравнения для определения изменения объемной доли в рамках термодинамики необратимых процессов Кинетическое соотношение (2.2.30), описывающее изменение объемной доли фазы, можно получить в рамках классической термодинамики необратимых процессов [12, 38]. При малых отклонениях от состояния равновесия неравновесные процессы в замкнутой системе могут быть описаны на основании весьма общих положений, высказанных впервые Онзагером. Для начала определимся с термодинамическим потенциалом, в терминах которого будут рассмотрены основные положения теории необратимых процессов в формулировке Онзагера. Выбор термодинамической функции состояния зависит от особенностей исследуемой проблемы. Для систем, находящихся в неизотермических условиях, обычно используется энтропия s . Для целей анализа необходимо определить, какие параметры в конкретных условиях влияют на поведение системы, т. е. с независимыми параметрами, от которых зависит термодинамический потенциал. Термодинамический потенциал гетерогенной системы в значительной степени зависит от ее фазового состава. В рассматриваемой задаче параметрами, характеризующими фазовый состав, являются объемные доли фаз 1 , 2 ,... . В начальный момент времени все зерна однофазны (аустенит). При фазовых превращениях в каждом зерне аустенит может полностью или частично перейти в новую фазу, т.е. зерна становятся многофазными и с ними работают как с гетерогенной средой. Под фазой в гетерогенной среде будем понимать область материала с определенной микроструктурой и гомогенными свойствами, отличными от свойств в других областях системы. Однако, помимо различия физических свойств, каждая фаза в равновесном состоянии имеет вполне определенный термодинамический потенциал, отличный от потенциала других фаз. Один из 67 важнейших процессов, происходящих при диффузионных фазовых превращениях в сталях, – это перераспределение углерода и легирующих элементов. Такое перераспределение также оказывает влияние на общее состояние системы, поэтому в качестве независимых аргументов при рассмотрении диффузионных превращений необходимо ввести концентрации углерода и легирующих элементов c1 , c2 ,... . При бездиффузионном фазовом превращении образующийся мартенсит содержит в растворе столько же углерода и легирующих элементов, сколько находится в исходном аустените. Поэтому изменения энтропии за счет диффузионного перераспределения углерода и легирующих элементов при мартенситном превращении не происходит. Одной из особенностей твердотельных фазовых переходов является возникновение полей внутренних напряжений, и стремление системы к снижению энергии упругой деформации. Поэтому в качестве аргумента термодинамической функции должна выступать упругая составляющая меры деформационного состояния qe . Таким образом, энтропия зависит от перечисленных выше переменных, т.е. s s 1 , 2 ,..., c1 , c2 ,..., e q e , , 1 , 2 ,..., c1 , c2 ,... , где e – внутренняя энергия. Перейдем к рассмотрению описания неравновесных процессов, исходя из общих соображений, высказанных Онзагером. Термодинамика необратимых процессов опирается на гипотезу локального равновесия. Эта гипотеза предполагает наличие равновесия в элементах пространственно неоднородных систем, возможность описания их состояния тем же набором термодинамических параметров, что и в состоянии равновесия, справедливость для этих элементов основных уравнений равновесной термодинамики. Данные элементы представляют собой части рассматриваемой термодинамической системы, которые достаточно малы для того, чтобы можно было говорить об однородности их состояния, при котором все термодинамические величины равны своим средним значениям по рассматриваемым элементам, но доста68 точно велики для того, чтобы существовала возможность использования для описания их состояния статистических методов. Состояние замкнутой системы характеризуется некоторыми макроскопическими параметрами zi (соотношения классической термодинамики устанавливаются для макроскопической системы), которые являются функциями времени. Если отклонения от состояния равновесия малы, то можно считать, что параметры, описывающие состояние системы, имеют термодинамический смысл. zi следует воспринимать как разность между значениями термодинамических величин в рассматриваемом неравновесном состоянии и в состоянии равновесия, где все термодинамические величины имеют значения, равные своим средним по термодинамической системе в целом. В том случае, когда отклонения от равновесного состояния малы, можно использовать термодинамические величины неравные своим средним значениям по термодинамической системе в целом. В случае малых значений zi величины, характеризующие состояние и изменение системы, можно разложить в ряд по степеням zi . В данных рядах должны удерживаться только первые члены, поэтому можно записать zi ik zk , s s0 ik zi z k , 2 s ik zi zk . В неравновесном состоянии энтропия системы определяется квадратичной формой, причем из второго условия следует ik ki , что использовано при получении третьего соотношения. Первое соотношение показывает, что вблизи состояния равновесия все процессы является медленным. Энтропия системы из-за необратимости процессов возрастает до тех пор, пока не достигнет максимально возможного значения. Достигнутое при этом состояние является состоянием равновесия. Все приведенные соотношения можно применять к описанию изменения состояния системы только за ограниченные 69 времена. Эти времена по сравнению с микроскопическими должны быть настолько велики, чтобы можно было говорить о существенном изменении макроскопических величин. С другой стороны из-за того, что рассматривается система, находящаяся в неравновесном состоянии, эти времена должны быть меньше времени установления полного равновесия в макроскопической системе. Обозначим через ji/ поток ji/ zi , а через xi/ так называемую термодинамическую силу xi/ s ik zk , zi тогда предыдущие соотношения можно представит в следующем виде ji/ ik zk ij jk1 xk/ ik xk/ , s s0 1 / xi zi , 2 s ji/ xi/ . В основе дальнейшего рассмотрения лежит гипотеза Онзагера, предполагающая то, что вблизи состояния равновесия неравновесное состояние можно трактовать как некоторую флуктуацию. Изменение во времени микроскопической системы, подвергнутой флуктуациям, и макроскопической системы, находящейся в неравновесном состоянии, происходит по одним и тем же законам. Для примера рассмотрим случай, когда в макроскопической системе концентрации и температуры распределены неравномерно. В этом случае в системе возникают потоки, которые описываются соответствующими макроскопическими законами переноса. Предположим, что в равновесной системе происходят флуктуации температуры или концентрации, в результате чего получается аналогичное распределение температуры и концентраций. Тогда из гипотезы Онзагера следует то, что эти флуктуации должны «рассасываться» по тем же законам, по которым в неравновесной макроскопиче70 ской системе осуществляется выравнивание температур и концентраций. Потоки температуры и частиц будут подчиняться законам теплопроводности и диффузии в независимости от того, возникли ли соответствующие разности в результате флуктуаций в равновесной системе или в результате внешнего воздействия. Таким образом, соотношение, связывающее силы и потоки вытекает из гипотезы Онзагера ji lik xk , и в равной мере может быть применимо, как к процессам «рассеивания» флуктуаций, так и к неравновесным системам. Средние силы и потоки xi и ji получены в результате усреднения xi/ и ji/ , а коэффициенты lik и ik совпадают. Кинетические коэффициенты также обладают свойством симметрии: lik lki . В случае записи кинетического уравнения для изменения объемной доли в качестве обобщенной силы можно принять щенной скорости – s x j , а в качестве обоб j i ji : t i m s lij . t j j 1 (3.1.1) Однако для того, чтобы в многофазной системе в каждой точке выполнялось равенство m i 1 , (3.1.2) i 1 необходимо применить технику множителей Лагранжа. Выражение (3.1.1) запишется следующим образом: m i s* s* s* s* s* lij li 1 ... li i-1 li i 1 ... li m , t j 1 j 1 i 1 i 1 m (3.1.3) где 71 m s* 0 s j 1 , j 1 (3.1.4) 0 , – множители Лагранжа. Соотношение (3.1.3) с учетом равенства (3.1.4) запишется в виде: s i s li 1 0 ... li i-1 0 t 1 i 1 (3.1.5) s s li i 1 0 ... li m 0 . i 1 m В многофазной системе состояние равновесия при некотором наборе параметров является устойчивым, если термодинамический потенциал принимает экстремальное (для энтропии – максимальное) значение, поэтому для определения нужно воспользоваться следующими соотношениями: 0 s 0. i (3.1.6) Примем, что 0 1 , тогда из соотношения (3.1.6) получим: s . i (3.1.7) Подставляя последнее выражение в (3.1.5), получим следующее соотношение для определения изменения фазовой доли в многофазной системе: s s s s i s s li 1 ... li i-1 li i 1 ... t i 1 i i 1 i i 1 (3.1.8) s s m s s li m . lij i m j 1 i j Для удобства моделирования конкретных систем перейдем в кинетическом уравнении от функции энтропии к функции свободной энергии (т. к. в термодинамических базах данных содержатся выражения именно для свободной энергии индивидуальной фазы, как функции от температуры и состава). Сначала запишем выражение для изменения внутренней энергии: e e e e de ds dc1 ... d1 ... e : dq . q c1 1 (3.1.9) 72 Используя связь между свободной и внутренней энергиями e f s , получаем следующее соотношение e e e df sd dc ... d ... : dq e . 1 1 e q c1 1 (3.1.10) Из этих соотношений можно установить следующие зависимости: s 1 e 1 f и т.д. 1 1 1 (3.1.11) Кинетическое уравнение (3.1.8) в терминах свободной энергии запишется следующим образом: m 1 f 1 f i lij t j j 1 i где разность , (3.1.12) f f является движущей силой фазового превращения j-й i j фазы в i-ю. Если f f 0 и 0 i 1, 0 j 1 , то происходит фазовое превращение i j j-й фазы в i-ю, объемную долю которой можно определить из решения уравнения (3.1.12). Если же f f 0 и i 1, j 0 , то превращение не проi j исходит. В модель для фазовых превращений можно ввести некоторый порог для движущей силы. Причиной возникновения этого порогового значения является взаимодействие движущейся границы с различного рода дефектами. В модели с введением порогового значения для движущей силы критерий фазового превращения и кинетическое уравнение запишутся следующим образом: m f f f f f f kij , то i lij sign kij , i j j 1 j i j i (3.1.13) 73 f f kij , то i 0 , i j (3.1.14) где kij – критическое значение движущей силы при превращении из j-й фазы в i-ю. Таким образом, в рассмотренном разделе приведены некоторые положения неравновесной термодинамики в формулировке Онзагера, на основании которых получено кинетическое уравнение для определения изменения объемной доли фаз, т. е. используется линейная связь скорости изменения объемной доли и производной термодинамического потенциала по данному параметру. В качестве термодинамической функции выбрана энтропия, определены независимые термодинамические параметры. Для удобства моделирования в кинетическом уравнении осуществлен переход от функции энтропии к функции свободной энергии. 3.2. Определение свободной энергии многофазной системы Предположим, что удельную свободную энергию можно представить в следующей форме: f 1 , 2 ,...,c1 , c2 ,...,q e , f EL f CH f S , (3.2.1) где f EL – упругая составляющая удельной свободной энергии, представляющая собой квадратичную форму от упругой составляющей меры деформированного состояния qe ; f CH – химическая составляющая, определяемая N как f CH i fi c1 , c2 ,..., , fi – удельная свободная энергии для i-й фазы; i 1 f S – поверхностная энергия. Определим свободную энергию для отдельной фазы f i . Для этого воспользуемся моделью [72, 95]: f i c1 , c2 ,..., fi чистый f i смеш fi взаим , (3.2.2) 74 где fi чистый – свободная энергия в отдельной фазе, fi смеш – вклад в свободную энергию за счет смешивания компонент, fi взаим – вклад в свободную энергию за счет химического взаимодействия отдельных компонент. Первое слагаемое в (3.2.2) может быть определено следующим образом: f i чистый 1 n p p ci fi vim p 1 (3.2.3) cip – концентрация p-го компонента стали (железа, углерода, легирующих элементов, примесей), измеряемая в молярных долях; fi p – свободная Дж N a vic м 3 энергия p-го компонента в i -й фазе, измеряемая в ; vim моль zi моль – молярный объем i-й фазы; N a – число Авогадро; vic – объем элементарной ячейки i-й фазы; zi – число атомов, приходящихся на элементарную ячейку iй фазы. Свободная энергия p-го компонента в i -й фазе может быть достаточно точно аппроксимирована следующей функцией [74]: fi p x1ip x2ip x3ip ln , (3.2.4) x1ip , x2ip , x3ip – константы. Второе слагаемое в выражении (3.2.2) отвечает за изменение свободной энергии за счет смешивания компонент на уровне атомов. Случайное изменение расположения атомов является причиной возникновения конфигурационной энтропии, изменение которой можно вычислить через логарифм числа возможных перестановок w: n! siконф k B ln wi k B ln 1 i p , ni !...ni ! где k B – константа Больцмана, n1i ,..., niр – количество молей соответствующего элемента, ni – общее количество молей. Для упрощения этого выражения воспользуемся формулой Стирлинга для больших чисел: 75 siконф R ci1 ln ci1 ... cip ln cip , R kB N a . Для всей системы мы получим: n конф i s R cip ln cip . p 1 Тогда изменение свободной энергии за счет смешивания компонент определиться следующим образом: fi смеш n 1 смеш 1 смеш h s R cip ln cip . i i vim vim p 1 (3.2.5) В данном случае энтропия системы siсмеш полностью определяется ее конфигурационной составляющей, а энтальпия hiсмеш 0 , т. к. химическая связь между атомами при описании изменения их расположения не важна. Третье слагаемое (3.2.2) описывает изменение свободной энергии за счет химического взаимодействия отдельных компонент. Будем рассматривать только парное взаимодействие и применим модель [100] для описания взаимодействия компонент друг с другом. Тогда изменение свободной энергии за счет химического взаимодействия компонент определится следующим образом: f i взаим 1 взаим 1 n1 n p j pj взаим h s i v p1 jp1 ci ci ri , i vim im (3.2.6) siвзаим 0 , т. к. энтропия системы полностью определяется ее конфигурационной составляющей, ri pj – параметр, описывающий взаимодействие между p и j компонентами в соответствующих фазах. Третье слагаемое в выражении (3.2.1) для свободной энергии (поверхностная энергия) в самом общем виде может быть записано следующим образом [109]: fS 1 ijk sijk , v k (3.2.7) 76 где ijk – удельная на единицу площади энергия границы между фазами i и j, занимающей область площадью sijk . В работе [110] предложено простое соотношение для определения поверхностной энергии, записанное в терминах объемной доли: m f S w i 1 i i 1 w m i 1 i , l i1 (3.2.8) , l – толщина границы. Равенство (3.2.8) выведено в предположении о l том, что кристаллы новой фазы представляют собой пластинки. В представленном разделе подробно рассмотрен вопрос записи свободной энергии многофазной системы. Считается, что свободная энергия определяется тремя составляющими: упругой, химической и поверхностной. Для каждой из этих составляющих приведены конкретные соотношения. 77 4. Алгоритм реализации модели 4.1. Общая структура алгоритма реализации двухуровневой модели На макроуровне – I ставится и решается краевая задача в обычном смысле (2.2.1) – (2.2.13). Задача диффузии на данном уровне не ставится и не решается, так как процесс перераспределения легирующих элементов на больших масштабах происходит очень медленно. Весь временной интервал при реализации алгоритма представляет из себя совокупность срезов по времени, на каждом из которых из решения задачи на макроуровне – I опреде- и скорость V , а также ее градиляются скорость изменения температуры ент V . Рассматриваемая конструкция покрывается дискретной сеткой. Для задачи определения НДС каждой макроскопической точке интегрирования ставится в соответствие элемент макроуровня – II, который представляет собой статистическую выборку элементов мезоуровня – отдельных зерен, т.е. используется прямая модель второго типа. Для задач диффузии и теплопроводности используется прямая модель первого типа, т. е. каждой точке интегрирования приписывается совокупность зерен с заданным распределением ориентаций, которым в свою очередь ставится в соответствие некоторая совокупность конечных элементов. Решение краевой задачи на макроуровне – I позволяет определить в каждой точке интегрирования градиент скорости перемещений, температуру и ее градиент после интегрирования уравнения теплопроводности, которые используются при решении задачи на следующем временном шаге. Для каждой из точек интегрирования на каждом шаге по времени решается четыре задачи: задача теплопроводности, задача диффузии, задача определения НДС и задача определения фазового состава. Ниже приведена общая структура алгоритма решения задачи на макроуровне – II. 78 Исходные данные: 1. Распределение температуры 2. Схема деформирования, определяемая градиентом относительной скорости перемещений (задан в ЛСК); 3. Фазовый состав 4. Ориентации кристаллических решеток элементов мезоуровня Дискретизация расчетной области для решения задач теплопроводности и диффузии для ПО макроуровня. Каждое зерно аппроксимируется совокупностью конечных элементов. Цикл по времени Температурная задача Входные данные 1. Значение температуры с макроуровня 2. Коэффициент теплоемкости (для зерна) 3. Тензор теплопроводности (для зерна) 4. Мощность внутренних тепловых источников (для зерна) Коэффициент теплоемкости, тензор теплопроводности и мощность внутреннего теплового источника для конечных элементов, покрывающих элемент мезоуровня, берутся одинаковыми. Формирование матриц теплоемкости, теплопроводности элемента и вектора тепловых нагрузок элемента. Учет периодических граничных условий. Сборка матриц теплоемкости, теплопроводности и вектора тепловых нагрузок всей системы. Решение системы линейных алгебраических уравнений. Определение температуры в конечном элементе как среднего арифметического температур в узлах элемента. Определение температуры в элементе мезоуровня (зерне) осреднением по всем элементам, аппроксимирующим зерно. 79 Задача диффузии Входные данные: 1. Значение температуры в каждом узле расчетной сетки 2. Тензор диффузии (для зерна) 3. Тензор термодиффузии (для зерна) Тензоры диффузии и термодиффузии для конечных элементов, покрывающих элемент мезоуровня, берутся одинаковыми. Формирование конечно-элементных матриц для элемента. Учет периодических граничных условий. Сборка конечно-элементных матриц всей системы. Решение системы линейных алгебраических уравнений. Определение концентрации в конечном элементе как среднего арифметического концентраций в узлах элемента. Определение концентрации в элементе мезоуровня (зерне) осреднением по всем элементам, аппроксимирующим зерно. Цикл по зернам при решении задач определения фазового состава и НДС (расчет каждого зерна производится в СК, связанной с решеткой аустенита) Задача определения фазового состава Входные данные: 1. Упругая составляющая меры деформации 2. Температура, определенная в зерне 3. Концентрация, определенная в зерне С использованием этих величин рассчитывается свободная энергия системы. Решение кинетического уравнения для определения доли фазы. 80 Задача определения НДС Входные данные: 1. Транспонированный градиент скорости перемещений (определяется согласно гипотезе Фойгта), переопределенный в терминах СК, связанной с решеткой аустенита 2. Температура, определенная в зерне 3. Напряжения, рассчитанные на конец предыдущего шага по времени 4. Физико-механические характеристики материала, рассчитанные на конец предыдущего шага по времени 5. Накопленные в процессе деформирования сдвиги по системам скольжения в зерне Физико-механических свойства материала 1. Переопределение физико-механических свойств каждой фазы в зависимости от значений температуры и концентрации, определенных в зерне; 2. Расчет свойств многофазного материала с использованием правила смеси. В ходе решения определяются: 1. Неупругая составляющая градиента относительной скорости перемещений 2. Термическая составляющая градиента относительной скорости перемещений 3. Тензора спина 4. Скорости изменения напряжений Определение мощности внутреннего источника тепла. Переопределение ориентационного тензора. Интегрирование закона Гука и определение напряжений на конец данного временного шага. Переопределение неупругой и термической составляющих градиента относительной скорости перемещений, тензора спина, физикомеханических характеристик отдельных зерен с учетом ротаций. 81 Конец цикла по зернам Определение параметров модели макроуровня в результате согласования ОС мезоуровня и макроуровня. Определение скорости напряжений и деформаций из закона Гука на макроуровне с использованием определенных явных переменных. Интегрирование соотношений в ЛСК. Проверка условия окончания счета - + Конец Далее приведены алгоритмы решения для каждой из подзадач. 4.2. Алгоритм решения задачи теплопроводности для представительного макрообъема При использовании прямой модели 1-го типа для ПО макроуровня, т. е. для элемента макроуровня –II, ставится и решается краевая задача для уравнения теплопроводности. В свою очередь элемент макроуровня – II представляет собой совокупность элементов мезоуровня – отдельных зерен с определенной ориентацией относительно ЛСК. Каждое зерно аппроксимируется совокупностью конечных элементов, поэтому краевая задача для элемента макроуровня – II ставится в терминах переменных мезоуровня. При решении температурной задачи для рассматриваемой области (2.2.34) в качестве входной информации используется температура , известная для каждой точки интегрирования на начало нового шага по времени после решения задачи на макроуровне – I. Также для решения краевой задачи необходимы теплофизические характеристики, а именно теплоемкость и тензор теплопроводности. Теплоемкость, тензор теплопроводности и мощность внутреннего теплового 82 источника зависят от объемных долей сосуществующих фаз и определяются по правилу смеси для каждого зерна, которое является элементом некоторой статистической выборки. При решении теплоемкость, тензор теплопроводности и мощность внутреннего теплового источника для конечных элементов, покрывающих элемент мезоуровня, берутся одинаковыми. При этом после определения ориентационного тензора для каждого элемента мезоуровня происходит переопределение тензора теплопроводности. После решения краевой задачи получаем значение температуры во всех узлах конечноэлементной сетки. Определенные значения температуры используются в качестве начальных при решении задачи на следующем временном шаге. В задаче диффузии дискретизация рассматриваемой области берется такой же, как и для задачи теплопроводности, поэтому при ее решении используются значения температуры, полученные при решении уравнения теплопроводности на рассматриваемом временном шаге. Для вычисления температуры в зерне и передачи этой информации в задачи определения фазового состава и НДС используется следующее осреднение. Сначала температура определяется в конечном элементе, как среднее арифметическое температур в узлах элемента. Затем находим температуру в элементе мезоуровня (зерне) осреднением по всем конечным элементам, аппроксимирующим зерно. На «выходе» в каждой точке интегрирования осреднением по ПО макроуровня вычисляются коэффициент теплоемкости, тензор теплопроводности, мощность внутреннего источника. Температура в каждом узле расчетной сетки определяется как: / . Значение величины нам известно в каждой точке интегрирования из решения задачи на макроуровне –I, поэтому уравнение теплопроводности для рассматриваемой области можно записать в терминах флуктуаций / (предполагается, что в начальный момент флуктуации отсутствовали): W 0 , C / K / C (4.2.1) 83 где / – вектор узловых флуктуаций температур всей области, N 1; N – общее число узлов расчетной сетки; n – число узлов конечного элемента; 1,2 ,...n – матрица функций формы, 1 n ; x 1 B – матрица производных функций формы, 3 n ; x2 x3 А – обозначение операции ансамблирования; C А – матрица теплоемкости всей области, N N ; C e T C e dV – матрица теплоемкости элемента, n n ; Ve – коэффициент теплоемкости, определяемый согласно (2.2.32); K А K e – матрица теплопроводности всей области, N N ; T K e B λ B dV – матрица теплопроводности конечного элемента, Ve nn; λ – матрица тензора теплопроводности, 3 3 , определяемая согласно (2.2.31); W АW e – мощность внутренних тепловых источников/стоков всей об- ласти, N 1; W e ydV – мощность внутренних тепловых источников/стоков коT Ve нечного элемента, n 1 . Мощность внутренних тепловых источников/стоков y определяется из выражения (2.2.33). 84 Для интегрирования системы обыкновенных дифференциальных уравнений (4.2.1) использована схема Крэнка–Николсона. Разностная схема в виде системы линейных алгебраических уравнений имеет вид: 2 / t t 2 4 K C C K C 2 K t t t t t t W W . При решении граничные условия выбираются так, чтобы выполнялось ограничение / ndГ 0 , поэтому на границе задаются периодические гра- Г ничные условия Г/ Г/ (знаки «+» и «-» соответствуют противоположным границам). В результате решения уравнения теплопроводности для представительного макрообъема на «выходе» в каждой точке интегрирования вычисляются параметры и характеристики макроуровня, а именно: коэффициент теплоемкости, тензор теплопроводности, мощность внутреннего источника: t t < t t > , Λ t t < λ t t > , Y t t < y t t > . С их использованием определяются матрицы теплоемкости, матрица теплопроводности и вектор тепловых нагрузок для физического тела при решении краевой задачи на макроуровне –I [18]. 4.3. Алгоритм решения задачи диффузии для представительного макрообъема Задача диффузии решается для той же области, что и задача теплопроводности; совпадает также и дискретизация рассматриваемой области. В начальный момент времени концентрации легирующих элементов берутся одинаковыми во всех узлах расчетной сетки. При решении задачи диффузии (2.2.35) – (2.2.37) используются значения температуры, известные из реше85 ния уравнения теплопроводности на рассматриваемом временном шаге в каждом узле конечно-элементной сетки, покрывающей рассматриваемую область. Уравнение диффузии также ставится для флуктуаций, но в отличие от задачи теплопроводности изменением концентрации на уровне физического тела пренебрегается. Из решения задачи диффузии определяются значения концентраций в каждом узле конечно-элементной сетки. Передача данных в задачи определения долей фаз и НДС осуществляется аналогично задачи теплопроводности. Таким образом, уравнение диффузии имеет следующий вид: S c cip / Lc cip / , где S c Lc c p/ АS ce (4.3.1) , N N ; S ce T dV , n n ; Ve АLce , N N ; L B T ce Ve dip B dV , n n , – вектор флуктуаций узловых концентраций ПО макроуровня, N 1; dip – матрица тензора диффузии, 3 3 . Остальные обозначения аналогичны обозначениям принятым для температурной задачи. Для интегрирования системы обыкновенных дифференциальных уравнений (4.3.1) использована явная схема. Разностная схема в виде системы линейных алгебраических уравнений имеет вид: S c p / t t S c p / t c p/ t ci Li ci t 2 ci . 2 При решении на границе задаются периодические граничные условия сiГp / ciГp / (знаки «+» и «-» соответствуют противоположным границам). 4.4. Определение фазового состава и напряженно- деформированного состояния на мезоуровне Скорость изменения объемных долей всех сосуществующих в отдельном зерне фаз определяется кинетическим уравнением (2.2.30). Значения са86 мих объемных долей определяются из следующих конечно-разностных соотношений, которые записываются для (N-1) сосуществующих фаз, а фазовая доля N-й фазы определяется из условия равенства единице суммы всех долей: it t 1 F it Lij t t j t t t , F F 1t t , 2t t ,..., c1t t , c2t t ,..., t t , qe t t . Для решения кинетического уравнения для определения доли фазы в каждом зерне необходимо найти свободную энергию многофазной системы. Свободная энергия зависит от упругой составляющей меры деформационного состояния qe , температуры и концентрации легирующих элементов, известных из решения задачи теплопроводности и диффузии на рассматриваемом временном шаге. Значения температуры и концентрации в зерне, которое передается в задачи определения фазового состава и НДС вычисляется следующим образом: сначала температура (концентрация) определяется в конечном элементе, как среднее арифметическое температур (концентраций) в узлах элемента, а затем в зерне – осреднением по всем конечным элементам, его аппроксимирующим. Параметры материала в многофазной системе зависят от фазового состава (2.2.22) – (2.2.23), (2.2.31) – (2.2.32): m пt t it t пi , i 1 m α t t it t α i , i 1 m λ t t it t λ i , i 1 m t t it t i . i 1 В свою очередь параметры материала отдельных фаз могут в значительной мере зависеть от температуры и концентрации легирующих элементов, по87 этому их необходимо переопределить в соответствии с найденными значениями. На каждом временном шаге решение задачи определения НДС включает следующие этапы: 1) с использованием модели мезоуровня определяются скорости неупругой и термической деформаций, скорости напряжений и спины элементов; 2) в ходе процедуры интегрирования определяются параметры процесса (напряжений, изменения ориентации элементов) на конец текущего – начало следующего временного шага; 3) изменения ориентаций элементов мезоуровня; нахождение в ОС макроуровня из замыкающих соотношений явных внутренних переменных. На каждом временном шаге «входной» информацией является информация о внешнем воздействии — транспонированный градиент скорости перемещений, известный из решения задачи на макроуровне – I; скорость изменения температуры , известная из решения задачи теплопроводности на рассматриваемом временном шаге; температура и концентрации легирующих элементов, известные для каждого кристаллита на начало рассматриваемого шага по времени. Также для решения задачи необходимы параметры процесса нагружения (напряжения и тензоры упругих свойств, переопределенные с учетом изменения ориентации решетки), рассчитанные на конец предыдущего шага по времени и накопленные в процессе деформирования сдвиги по СС в зерне. В результате использования модели мезоуровня на «выходе» определяются неупругая и термическая составляющие транспонированного градиента скорости перемещений ζinr , ζthr , тензор спина ω и скорости изменения напряжений σ , с учетом ротаций переопределяются также тензоры упругих свойств отдельных зерен. Кроме того, необходимо определить мощность внутреннего теплового источника, которая зависит не только от протекающих фазовых превращений, но и от пластической деформации (2.2.33). 88 В качестве элемента мезоуровня рассматривается зерно. Использование в рамках модели (расширенной) гипотезы Фойгта приводит к соотношению: ζΖ. Поскольку компоненты градиента скорости перемещений для ПО макроуровня определены в ЛСК, то для того, чтобы на мезоуровне задать воздействия необходимо их преобразовать в СК, связанную с решеткой аустенита, т. к. при рассмотрении фазовых превращений все величины принято записывать в базисе родительской фазы. Система уравнений, в которую входят соотношения (2.2.19), (2.2.20), (2.2.24), (2.2.25), (2.2.29), на каждом шаге по времени разрешается в скоростях. Такие величины, как тензор упругих свойств, градиент трансформационной деформации и др. определяются в СК, связанной с решеткой аустенита, для упрощения записи соотношений мезоуровня. Кроме того, вследствие перехода к решеточному базису (аустенита) в законе Гука исчезают слагаемые ω σ, σ ω , поскольку коротационная производная определяет скорость изменения компонент тензора относительно подвижного наблюдателя (в данном случае – связанному с решеткой аустенита). Неупругая и термическая составляющие градиента относительной скорости перемещений в многофазной системе определяется из уравнений: t t ζ in r th r i t t i t t ζ m1 n m2 k 1 i t t it(k )t Pi k i fi* , α t t , где Pi k b i k n i k . При этом скорости сдвига вычисляются как: t t k i k 0i H t t k i t t c k i tki t t t c k i 1 mci . t t t t t t Здесь tki t Pi k : σ , ct k i c k i f i , j , k , t , 89 t t t где f ti , j , k , – функция, которая определяется одним из законов уп- рочнения (2.2.25) – (2.2.27). Тензор спина решетки рассчитывается с помощью соотношения: t t ω *t t w 1 N1 t t n t t k k k k i k i bi ni ni bi . 2 i1 k 1 В результате интегрирования соотношения (2.2.19) в СК, связанной с решеткой аустенита, по известным транспонированному градиенту относительной скорости перемещений и его неупругой и термической составляющим, находим напряжения на конец данного временного шага: t t σ t σ п : ξ r ξ inr ξ thr t . Для интегрирования соотношения (2.2.28) применяется следующий алгоритм. Сначала как ассоциированный вектор для тензора спина ω находит- 1 ся вектор угловой скорости χ : χ t Є : ωt ( Є – тензор Леви–Чивита). По 2 вектору угловой скорости рассчитывается единичный вектор оси скорости (приращения) поворота e r 1 r χ t χ t t t и угол поворота ре r 2 шетки из текущего положения . Ортогональный тензор ротации R определяется по рассчитанным значениям компонент вектора e (с использованием тензора ротации R находится поворот решетки относительно именно этого вектора) и углу поворота : R t cos t I 1 cos t ee sin t e I . Ориентационный тензор решетки переопределяется с использованием вычислительного тензора ротации: ot t R ot . После переопределения ориентационных тензоров происходит преобразование явных внутренних переменных из СК, связанной с решеткой аустенита, в ЛСК. 90 Стоит отметить, что величины, входящие в вышеприведенные соотношения, могут зависеть как от температуры, так и от концентрации легирующих элементов, поэтому до решения они должны быть переопределены в соответствии со значениями , cip с использованием имеющихся в литературе экспериментальных зависимостей. Мощность внутреннего теплового источника определяется как: y t t m1 i 1 n t t i t t k i t t k i k 1 m2 H ii . i 1 В результате решения задачи по определению НДС на мезоуровне на «выходе» в каждой точке интегрирования вычисляются параметры и характеристики макроуровня, а именно: тензор упругих свойств, тензор спина, неупругая составляющая градиента относительной скорости перемещений, термическая составляющая градиента относительной скорости перемещений: П t t < S : пt t > , Ωt t < ωt t > , Z < ζ > < α П :< S : п : ζ in r t t t t in r t t 1 1 / / t t t t П t t :< ω / in / r t t σ /s t t t t > ω/ t t σ /s t t α / ω/ t t t t > >, Z thr < ζ r th > + П 1 : S п/ : ζr th / . С их использованием определяются матрица жесткости и вектор нагрузок физического тела при решении краевой задачи на макроуровне – I [18]. Представлены алгоритмы численной реализации предложенной модели для всех подзадач на всех рассматриваемых масштабных уровнях. При реализации модели все подзадачи, по сути дела, рассматриваются отдельно и решаются последовательно: температурная задача, задача диффузии, задача определения фазового состава и задача определения НДС. 91 5. Результаты численных экспериментов с использованием двухуровневой модели Перечислим параметры, необходимые для расчетов конкретных процессов с использованием рассмотренной модели. Для применения соотношения, описывающего кинетику фазового превращения, необходимы следующие данные: 1) кинетические коэффициенты lij , МПа-1с-1; 2) параметры, фигурирующие в выражениях: – для свободной энергии отдельной фазы: x1ip , x2ip , x3ip и rpji ; – для свободной энергии за счет взаимодействия между различными фазами: w , МПа; Выражение для свободной энергии индивидуальной фазы, как функции от температуры и состава, можно найти в базе TCFE, встроенной в пакет Thermo-Calc (http://www.thermocalc.com). Материальный параметр w определяется отношением энергии границы ( , Дж/м2) к толщине границы ( l , м). Энергия границы определяется экспериментально, а толщина границы является подгоночным параметром, характеризующим особенности межфазной границы. Кинетические коэффициенты lij определяются отношением, связывающим скорость перемещения межфазной границы и движущую силу фазового превращения. Для решения задачи о перераспределении легирующих элементов и углерода в ходе фазового превращения необходимы компоненты тензора диффузии d p rs i , м2/с. Они определяются экспериментально и их значения мож- но найти в такой базе как MOBFE, которая встроена в пакет DICTRA (http://www.thermocalc.com). Для решения температурной задачи необходимы значения следующих величин: 1) теплоемкость i , Дж/м3 оС; 92 2) компоненты тензора теплопроводности i pq , Вт/м оС; 3) скрытая теплота фазового перехода gi , Дж/кг, которые берутся из экспериментальных работ других исследователей. Для решения задачи определения НДС необходимы следующие данные: 1) компоненты тензора упругих свойств пipqrs , ГПа и тензора термического расширения ipq , оС-1 для всех сосуществующих фаз; 2) параметры, фигурирующие в законе для определения скорости сдвиговой деформации: – параметр скоростной чувствительности mci ; – скорость сдвига 0i , с-1 при напряжении, равном критическому; 3) параметры закона упрочнения: – ; – модули упрочнения a ji , МПа; k – начальный предел текучести сi 0 , МПа; k – материальные константы Bi , с-1; mi ; ˆci , МПа – энергия активации диффузии Qi , Дж/моль; – параметр, характеризующий упрочнение в родительской фазе за счет образования новой фазы H i , МПа. Значения компонент тензора упругих свойств и тензора термического расширения, скорости сдвига при напряжении, равном критическому, параметра скоростной чувствительности, а также начальный предел текучести считаются известными и берутся из работ других исследователей. Значения остальных параметров в законе упрочнения определены в ходе процедуры идентификации. Процедура идентификации параметров осуществляется на основе экспериментальных данных по одноосному растяжению. Рассматриваемые эксперименты по одноосному растяжению/сжатию образца проводятся при по93 стоянной температуре; считается, что изменение температуры образца может происходить за счет пластической деформации и фазовых превращений. Процедура идентификации предполагает решение задачи минимизации: i u * i 2 min , i где * – значение напряжений, определяемое при интенсивности деформации ε, по диаграмме нагружения, построенной на основании экспериментальных данных; u – рассчитанная с помощью модели интенсивность напряжений; i – номер точки на экспериментальной диаграмме нагружения. 5.1. Идентификация и верификация модели на примере мартенситного превращения при деформировании стали AISI 304 Процедура идентификации и верификации модели применительно к бездиффузионным (мартенситным) фазовым превращениям (рис. 9) осуществляется с использованием экспериментальных данных [101] по одноосному растяжению образцов стали AISI 304, химический состав которой приведен в таблице 1. Эксперименты проводят при комнатной температуре; изменение температуры образца происходит за счет пластической деформировании аустенита и мартенсита. Таким образом, рассматриваемые превращения происходят только за счет внешнего механического воздействия. Рис. 9. Превращение кубической решетки аустенита в тетрагональную решетку мартенсита 94 В недеформированном состоянии образец из стали AISI 304 содержит только аустенит. Средний размер зерна был определен с использованием метода сканирующей электронной микроскопии и дифракционного метода обратного рассеяния электронов и составляет 1210-6 м. Кроме того, с помощью ренгеноструктурного анализа было показано, что в недеформированном состоянии в аустените текстура отсутствует. На стадии идентификации используются экспериментальные кривые «напряжение-деформация» для аустенита и мартенсита, полученные при одноосном растяжении образца (размеры активной части 3041 мм) со скоростью деформирования 10-5 с-1 при температуре 20 оС (in situ tensile test). В in situ испытаниях на одноосное растяжение образец помещают в испытательную микромашину. Такой тип эксперимента позволяет проводить испытания с низкой скоростью деформирования и определять напряжения в отдельных фазах, измеряя их на поверхности образца, помещая испытательную микромашину под PROTO гониометр. Определение доли образующегося при деформировании мартенсита происходит с помощью сканирующей электронной микроскопии. Таблица 1 Химический состав стали AISI 304 С Mn Cr Ni Массовый 0.06 1.54 18.47 8.30 процент Mo 0.30 Cu 0.37 Nb 0.03 Si 0.48 Fe Bal. Моделирование одноосного деформирования производилось для ПО макроуровня, состоящего из 3375 зерен. В случае одноосного растяжения при жестком нагружении известной является только одна компонента градиента , скорости перемещений Z11 =10-5 с-1; кроме того, все компоненты тензора Σ ij , являются нулевыми; остальные компоненты градиента скорости кроме Σ 11 определяются из решения системы перемещений и компонента тензора Σ 11 алгебраических уравнений, построенной на основе закона Гука. 95 Рассматриваемые эксперименты проводились при комнатной температуре и полагалось, что изменение температуры образца может происходить как за счет пластической деформации аустенита и мартенсита, так и за счет протекающих фазовых превращений, поэтому для оценки этого изменения использовалось уравнение теплопроводности, записанное в следующем виде: m1 n m2 i 1 k 1 i 1 i i k i k i g ii . Выражение для свободной энергии индивидуальной фазы, как функции от температуры и состава, можно найти в базе TCFE, встроенной в пакет Thermo-Calc (http://www.thermocalc.com). Значение параметра w принято равным 4106 Дж/м3 для всех разновидностей мартенсита [105]. Кинетические коэффициенты lij одинаковы для всех вариантов мартенсита и равны 10 МПа-1с-1 [71]. Теплота фазового перехода g i =82103 Дж/кг также берется одинаковой для всех разновидностей мартенсита [81]. Значения следующих параметров для аустенита и мартенсита были взяты из работ других исследователей: коэффициент теплоемкости – из [13, 115], компоненты тензора упругих свойств – [86, 106] и тензора термического расширения – [115], параметра скоростной чувствительности, начальный предел текучести – [88], скорости сдвига при напряжении, равном критическому. Значения остальных параметров в законе упрочнения определялись в ходе процедуры идентификации. Все параметры модели, необходимые для описания процессов деформирования с учетом мартенситного превращения, приведены в таблице 2. На стадии верификации используются экспериментальная кривая «напряжение–деформация» для стали, полученная при одноосном сжатии образца со скоростью деформирования 10-1 с-1 при температуре 20 оС (macroscopic tensile test). Для макроскопических испытаний на одноосное сжатие используется универсальная испытательная машина. В процессе деформирования для отслеживания мартенситного превращения, происходящего в процессе 96 деформирования, производилась съемка с помощью высокоскоростной инфракрасной камеры. Таблица 2 Параметры модели Аустенит Параметр решетки, A a A 3.56 A A A Компоненты тензора упругих п1111 204.6, п 2222 137.7, п1212 126.2 свойств, ГПа Параметр скоростной чувстви- m 0.02 сA тельности Скорость сдвига при напряжении, 0 A 105 равном критическому, с-1 Начальный предел текучести, МПа cA0 300 Коэффициент теплоемкости, A 3.925 106 Дж м 3 о С 1 Компоненты тензора термическо- 11A 22A 33A 106 го расширения, о С 1 Параметр A А 6.399 10 6 Модули упрочнения aii A , aki A i aiAi 3.822 102 , akA 4.778 102 Параметры BA , 1 ; m A ; ˆc A , МПа с BA =4.080 103 ; mA 3.023; ˆcA 201.533 Энергия активации QA , кДж моль QA 89.997 Мартенсит aM 2.85 Параметры решетки, A M M M M Компоненты тензора упругих п1111 п3333 422.5, п1133 344.3, п1122 п M2233 225.3, свойств, ГПа (в базисе, связанном M M M M п2222 524.5, п1212 п2323 223.6, п1313 244.0 с собственной решеткой) Параметр скоростной чувствиmсМ 0.02 тельности Скорость сдвига при напряжении, 10 5 0М равном критическому, с-1 Начальный предел текучести, МПа сМ 0 500 Коэффициент теплоемкости, М 3.3325 10 6 3 о 1 Дж м С Компоненты тензора термическо- 11М 22М 0.15 106 , 33М 0.6 106 го расширения, о С 1 Параметр Ì M 6.830 106 Модули упрочнения aii М , aki М i i aiM 1.433 10 2 , akM 1.147 102 Параметр BМ , 1 ; mМ ; ˆc М , МПа с BM =3.400 103 ; mM 2.335; ˆcM 335.888 Энергия активации QМ , кДж моль QM 92.200 97 Предполагалось, что в процессе деформирования может образовываться мартенсит 3-х вариантов, соответствующих трем возможным деформациям Бейна (рис. 10). Вид решетки аустенита и мартенсита Матрицы упругих свойств аустенита и мартенсита (для мартенсита определены в базисе связанном с его собственной решеткой, ГПа) Трансформационные матрицы (определены в базисе связанном с решеткой аустенита) 1 2a a , 3 a a A п1111 204.6 A п 2222 137.7 A п1212 126.2 M M п2222 п3333 422.5 п M 2233 344.3 M M п1122 п1133 225.3 3 0 0 f1 0 1 0 0 0 1 M п1111 524.5 M M п1212 п1313 223.6 M п2323 244.0 М М п1111 п3333 422.5 М п1133 344.3 М М п1122 п2233 225.3 М п2222 524.5 1 0 0 f 2 0 3 0 0 0 1 М М п1212 п2323 223.6 М п1313 244 М п1111 пМ2222 422.5 М 1122 344.3 М 1133 М п2233 225.3 п п 1 0 0 f3 0 1 0 0 0 3 М п3333 524.5 М М п1313 п2323 223.6 М п1212 244 Рис. 10. Превращение кубической решетки аустенита в тетрагональную решетку мартенсита 98 В несимметричном тензоре упругих свойств мартенсита рассматривалось отклонение компонент от их среднего значения: 1313 и 3131, 1212 и 2121 для первого варианта; 1313 и 3131, 2323 и 3232 для второго варианта; 1212 и 2121, 2323 и 3232 для третьего варианта. Значение компонент 1212, 1313, 2323 были увеличены на 5%, а значения компонент 2121, 3131, 3232 на 5% были уменьшены во всех случаях. Отклонения связываются с геометрическими размерами решетки. Если взять простую модель упругих стержней с жесткостями, обратно пропорциональными их длине, то жесткость при сдвиге вдоль длинных ребер должна быть выше, чем при сдвиге вдоль коротких. Для аустенита использовался симметричный тензор упругих свойств. На рис. 11, 12 представлены результаты натурного эксперимента и кривые, полученные в результате решения задачи оптимизации в ходе проведения процедуры идентификации для аустенита и мартенсита. Стоит отметить, что при интенсивности деформаций менее 0.35 напряжения для мартенсита экспериментально определены не были из-за небольшой доли образовавшегося мартенсита, поэтому при решении задачи оптимизации производилась экстраполяция имеющихся экспериментальных данных для определения напряжений при интенсивности деформаций, меньшей 0.35. Рис. 11. Кривая «интенсивность напряжений–интенсивность накопленных деформаций» для аустенита (точки соответствуют экспериментальным данным) 99 Рис. 12. Кривая «интенсивность напряжений–интенсивность накопленных деформаций» для мартенсита (точки соответствуют экспериментальным данным) На рис. 13 приведена кривая «напряжение–деформация», полученная в ходе процедуры верификации модели, когда вычислительный эксперимент по одноосному сжатию проводился с параметрами, полученными идентификацией, сравнение результатов моделирования производилось с результатами, приведенными в статье [79]. Максимальное отклонение кривой, полученной в численном эксперименте, по отношению к экспериментальной составляет порядка 13%. На рис. 14 приведена зависимость объемной доли образовавшегося мартенсита (берется осредненное по всем вариантам значение) от интенсивности накопленных деформаций. Рис. 13. Кривая «интенсивность напряжений–интенсивность накопленных деформаций» для стали (точки соответствуют экспериментальным данным) 100 Рис. 14. Зависимость доли образовавшегося мартенсита от интенсивности накопленных деформаций (точки соответствуют экспериментальным данным) Таким образом, были рассмотрены вопросы идентификации и верификации модели. На основе данных натурного эксперимента в случае мартенситного превращения, происходящего при внешнем механическом воздействии, была проверена ее адекватность. При этом соответствие между результатами расчета и данными натурного эксперимента можно считать удовлетворительным. 5.2. Моделирование поведение стали AISI 301 при простом и сложном нагружении с учетом мартенситных превращений С использованием разработанного алгоритма и программы его реализации осуществлено моделирование деформирования ПО макроуровня в опытах на сложное нагружение (растяжение-сдвиг, сдвиг-растяжение). ПО состоял из 3375 зерен, шаг интегрирования составлял 0,05 с. В качестве моделируемого материала во всех численных экспериментах выступала сталь AISI 301 (состав приведен в таблице 3), физико-механические свойства которой можно найти на сайте www.aksteel.com. Численные эксперименты проводились для комнатной температуры, при этом полагалось, что изменение температуры образца может происходить за счет пластической деформации аустенита и мартенсита, а также протекающих фазовых превращений. Параметры модели для описания поведения стали AISI 301 берутся из таблицы 2. 101 В случае одноосного растяжения при жестком нагружении известной является только одна компонента градиента скорости перемещений Z11 =1,310-4 с-1; , кроме Σ , являются нулевыми; оскроме того, все компоненты тензора Σ ij 11 тальные компоненты градиента скорости перемещений и компонента тензора определяются из решения системы алгебраических уравнений, построенΣ 11 ной на основе закона Гука. При моделировании простого сдвига реализовано жесткое нагружение Z12 =-0,510-5 с-1, Z ij 0, ij 12 . Предполагалось, что в процессе деформирования может образовываться мартенсит трех вариантов, соответствующих трем возможным деформациям Бейна (рис. 10). Таблица 3 Химический состав стали AISI 301 С Mn Cr Ni Массовый 0.15 2.00 16.00 6.00 процент N 0.10 P 0.05 Si 0.75 S 0.03 Fe Bal. При исследовании сложного нагружения было рассмотрено несколько случаев: процесс «растяжение–сдвиг» для различных уровней интенсивности деформации первого этапа (0.068, 0.085) и процесс с обратным порядком нагружения, то есть «сдвиг–растяжение». На рис. 15 и 16 приведены зависимости интенсивности напряжений и объемной доли образовавшегося мартенсита (осредненного по всем вариантам) от интенсивности накопленных деформаций для трех описанных выше случаев. На рис. 17, 18 для сравнения представлены аналогичные зависимости для случаев одноосного растяжения и простого сдвига. 102 Рис. 15. Кривая «интенсивность накопленных деформаций–интенсивность напряжений» для следующих случаев: растяжение (до интенсивности 0.068) – сдвиг ( ), растяжение (до интенсивности 0.085) – сдвиг ( ), сдвиг (до интенсивности 0.068) – растяжение ( ) Рис. 16. Зависимость доли образовавшегося мартенсита от интенсивности накопленных деформаций для следующих случаев: растяжение (до интенсивности 0.068) – сдвиг ( 0.085) – сдвиг ( ), растяжение (до интенсивности ), сдвиг (до интенсивности 0.068) – растяжение ( ) Рис. 17. Кривая «интенсивность накопленных деформаций–интенсивность напряжений» для случая одноосного растяжения ( ) и простого сдвига ( ) 103 Рис. 18. Зависимость доли образовавшегося мартенсита от интенсивности накопленных деформаций для случая одноосного растяжения ( ) и простого сдвига ( ) Как видно из рис. 15, после излома траектории деформирования наблюдается характерное снижение интенсивности напряжений. Можно отметить, что при изменении уровня предварительной деформации характер зависимости интенсивности напряжений от интенсивности деформаций не меняется, доля образовавшегося мартенсита отличается максимум на 8%. Также следует отметить, что во всех трех случаях доля образовавшегося мартенсита меньше, чем в случае и одноосного растяжения, и простого сдвига. Возможно, основное влияние на наблюдаемые зависимости оказывают процессы разворотов кристаллических решеток зерен и изменение микроструктуры. После излома траектории из-за появившегося изменения микроструктуры материала скольжение по некоторым системам замораживается, а вместо них включаются другие. То, что ни в одном случае объемная доля образовавшегося мартенсита не достигает значений, полученных при простом нагружении, можно объяснить тем обстоятельством, что при деформировании на первом участке разворот кристаллических решеток может привести к появлению преимущественного направления, поэтому при смене траектории деформирования рост объема мартенсита менее интенсивен, чем в случае простого нагружения. Рассмотрим более подробно процессы фазового превращения в представительном макрообъеме для случая простого нагружения (одноосное растя104 жение) и сложного нагружения (растяжение до интенсивности 0.068 – сдвиг). На рис. 19, 20 показано распределение объемных долей трех разновидностей мартенсита по ПО макроуровня в различные моменты процесса нагружения. Как видно из рис. 19, до интенсивности накопленных деформаций равной 0.1 увеличение объемной доли мартенсита происходит за счет начала превращения во все новых и новых зернах. Когда интенсивность накопленных деформаций превышает значение 0.1, увеличение объемной доли мартенсита в основном происходит не за счет его образования в новых зернах, а за счет более интенсивного протекания фазовых превращений в зернах, где уже содержится некоторая доля новой фазы. Рис. 19. Распределение объемных долей мартенсита по представительному макрообъему 105 Как было отмечено выше, при сложном нагружении доля образовавшегося мартенсита значительно меньше, чем в случае одноосного растяжения и простого сдвига. Это можно объяснить тем, что в зернах, где мартенсит образовывался до смены траектории нагружения, фазовые превращения после смены идут не так активно. Вместо этого образование мартенсита происходит в новых зернах, за счет чего в основном и увеличивается объемная доля новой фазы. Отмеченные зависимости можно наблюдать на рис. 20. Рис. 20. Распределение объемных долей мартенсита по представительному макрообъему Для анализа процессов на мезоуровне рассмотрим два зерна: благоприятно и неблагоприятно ориентированных по отношению к внешней нагрузке (случай одноосного растяжения). Для пояснения термина «благоприятная ориентация» обратимся к рис. 21: при сжатии тетрагональной ячейки вдоль направления [001] и одновременном растяжении по направлениию 110 , ее тетрагональность будет постепенно уменьшаться и в пределе получится ячейка ОЦК решетки. Экспериментально показано, что наибольшее количе106 ство мартенсита образуется в том случае, если ось сжатия соответствующего варианта близка к направлению приложения нагрузки. На рис. 22, 23 приведены зависимости доли образовавшегося мартенсита каждого из трех вариантов и интенсивности напряжений от интенсивности деформаций для обоих зерен. Рис. 21. Схема перестройки решетки ГЦК в решетку ОЦК 107 Рис. 22. Зависимость доли образовавшегося мартенсита трех различных разновидностей для зерна с благоприятной и неблагоприятной ориентацией в различные моменты процесса Рис. 23. Кривая «интенсивность накопленных деформаций – интенсивность напряжений» для зерна с благоприятной ( ) и неблагоприятной ( ) ориентацией в случае одноосного растяжения Из рис. 22, 23 видно, что наибольшее количество мартенсита образуется, если ось сжатия соответствующего варианта близка к направлению приложе108 ния нагрузки (благоприятная ориентация). Количество двух остальных вариантов мартенсита практически одинаково. При неблагоприятной ориентации зерна доля 2 и 3 вариантов также практически одинакова, объемная доля первого варианта больше остальных максимум на 7%, однако это значительно меньше, чем в случае зерна с благоприятной ориентацией (максимум на 50%). Также из рис. 23 видно, что уровень напряжений в зерне с благоприятной ориентацией по отношению к внешней нагрузке выше, что может быть связано с увеличением объемной доли жесткой мартенситной фазы, обладающей высоким пределом текучести (конечно же, подобная зависимость не всегда справедлива, так как напряжения могут расти и за счет взаимодействия с соседними зернами, имеющими отличную ориентацию). Для исследования влияния несимметрии тензора упругих свойств на поведение материала был проведен ряд вычислительных экспериментов по одноосному растяжению монокристалла, по-разному ориентированного относительно оси нагружения. Считается, что пластически деформироваться может только аустенит. При этом нагружение осуществлялось вдоль оси ОХ3 ЛСК, ориентация кристаллической решетки определялась углом между осями Ох3 и ОХ3 СК, связанной с решеткой аустенита, и ЛСК соответственно при совмещении осей Ох1 и ОХ1 (рис. 24). Рис. 24. Взаимное расположение осей ЛСК и СК, связанной с решеткой аустенита 109 На рис. 25, 26 приведены диаграммы деформирования монокристалла с использованием симметричных и несимметричных тензоров упругих свойств при различных ориентациях СК, связанной с решеткой аустенита монокристалла относительно ЛСК (15о, 30о). В несимметричном тензоре упругих свойств рассматривалось незначительное отклонение выделенных компонент от симметричного случая. Для аустенита значение компоненты 1212 было увеличено на 1%, а значение компоненты 1221 на 1% было уменьшено. В несимметричном тензоре упругих свойств мартенсита значения компонент 1212 (для первого варианта), 1313 (для второго варианта), 2323 (для третьего варианта) были увеличены на 1%, а значения компонент 2121 (для первого варианта), 3131 (для второго варианта), 3232 (для третьего варианта) на 1% были уменьшены. Анализ зависимостей интенсивности напряжений от интенсивности деформаций показывает, что при использовании несимметричных мер напряженно-деформированного состояния с несимметричным тензором упругих характеристик (при незначительном отклонении выделенных компонент от симметричного случая) отклонение характеристик процесса по сравнению с симметричным случаем достаточно существенно (по сравнению с изменениями самих модулей упругости), и составляет для ориентации 15о – 5%, а для ориентации 30о – 3.5%. Для обоих случаев характер поведения кривых «напряжения-деформации» схож. Так, можно отметить, что в «несимметричном» случае интенсивное упрочнение наблюдается при большем значении интенсивности накопленных деформаций в сравнении с «симметричным» случаем. Объемные доли образующегося мартенсита также ниже в случае использования несимметричного тензора упругих характеристик (рис.27, 28). 110 Рис. 25. Зависимость интенсивности напряжений от интенсивности накопленных деформаций для симметричного ( ) и несимметричного ( ) случаев при ориентации 15о Рис. 26. Зависимость интенсивности напряжений от интенсивности накопленных деформаций для симметричного ( ) и несимметричного ( ) случаев при ориентации 30о 111 Рис. 27. Объемные доли трех вариантов мартенсита для несимметричного и симметричного случаев при ориентации 15о Рис. 28. Объемные доли трех вариантов мартенсита для несимметричного и симметричного случаев при ориентации 30о 112 Проведем более детальный анализ процессов деформирования в монокристалле. На рис. 29 представлена зависимость накопленного сдвига по активным СС в случае использования симметричного и несимметричного тензора упругих свойств, для ориентации, соответствующей 15о. Заметно, что в несимметричном случае сдвиги происходят по 4 СС, тогда как в симметричном случае число активных систем равно 3. Таким образом, при использовании несимметричной меры скоростей деформаций и напряжений в материале в процессе неупругого деформирования на мезоуровне появляется большее число степеней свободы. Следует отметить, что суммарный сдвиг в приведенной ориентации в симметричной теории несколько больше, что в конечном счете приводит к отклонениям, наблюдаемым на кривой «интенсивность накопленных деформаций – интенсивность напряжений». Рис. 29. Зависимости накопленного сдвига по активным СС от интенсивности накопленных деформаций при ориентации 15о ( несимметричный случай, симметричный случай). Нумерация систем приведена в таблице 4 Стоит отметить, что если рассматривать поведение материала на мезоуровне при тех же условиях эксперимента в случае использования несимметричного тензора упругих свойств без учета происходящих фазовых превращений, то можно заметить, что скольжение происходит по 8 активным СС (рис. 30). Таким образом, даже небольшое количество образующегося мартенсита может стать причиной изменения пластического поведения родительской фазы, т. к. образование новой фазы может стать причиной появле113 ния препятствий для скольжения дислокаций и вызвать значительное изменение локальных полей напряжений. Таблица 4 Компоненты вектора Бюргерса и нормали СС в ГЦК решетке Номер СС 1 110 111 СС Номер СС 13 1 10 111 СС 2 0 11 111 14 01 1 111 3 10 1 111 15 101 111 4 0 11 111 16 01 1 111 5 10 1 111 17 101 111 6 110 111 18 1 10 111 7 10 1 11 1 19 101 11 1 8 1 10 11 1 20 110 11 1 9 21 0 1 1 11 1 10 011 11 1 011 1 11 22 011 1 11 11 10 1 1 11 23 10 1 1 11 12 110 1 11 24 110 1 11 Рис. 30. Зависимости накопленного сдвига по активным СС от интенсивности накопленных деформаций при ориентации 15о. Нумерация систем приведена в таблице 4 Таким образом, в приведенном разделе представлены результаты моделирование деформирования ПО макроуровня в опытах на простое и сложное нагружение для стали AISI 301. Проанализированы процессы, происходящие на мезоуровне, рассмотрен вопрос о влиянии несимметрии тензора упругих свойств на поведение материала. 114 5.3. Моделирование поведения стали с учетом диффузионного ферритного превращения С помощью представленной модели был исследован процесс образования феррита в стали, состав которой приведен в таблице 5, при одноосном сжатии образца при высокой температуре (760-800 0С) в ПО макроуровня (343 зерна). В рассматриваемом процессе температура меняется в результате пластической деформации аустенита и феррита и за счет выделения теплоты в ходе фазового превращения. Трансформационная составляющая градиента относительной скорости перемещения определялась следующим образом: ζtrr 1 3 I, 0.01 . Таблица 5 Химический состав стали С Mn Al N P Массовый 0.1 1.43 0.03 0.0056 0.016 процент S 0.003 Si 0.31 Fe Bal. При идентификации параметров закона упрочнения для аустенита (кроме начального предела текучести) рассматривался процесс одноосного сжатия образца со скоростью деформирования 310-3 с-1 при температуре 800 оС, т. к. в рассматриваемом случае доля образующегося феррита мала (3%) и его влиянием на процессы деформирования можно пренебречь. При идентификации параметров закона упрочнения для феррита рассматривался процесс одноосного сжатия образца со скоростью деформирования 310-3 с-1 при температуре 760 о С. На стадии верификации использовалась кривая «напряжение- деформация», полученная при одноосном сжатии образца со скоростью деформирования 310-4 с-1 при температуре 760 оС. Все экспериментальные зависимости были взяты из работы [87]. Значение параметра w принято равным 2106 Дж/м3 [103]. Кинетический коэффициент l равен 10 МПа-1с-1 [71]. Теплота фазового перехода g равна 82103 Дж/кг [81]. Коэффициенты теплоемкости и термического расширения стали при температуре 760 оС равны 115 =8.68106, Дж/м3 оС и =14.5410-6, оС-1; при температуре 800 оС – =6.00106, Дж/м3 оС и =12.4010-6, оС-1. При моделировании учтена происходящая при фазовом превращении диффузия углерода ( d AC =210-12 м2/с) и марганца ( d AMn =4.110-18 м2/с) в аустените [103]. Дополнительно учитывается зависимость коэффициента диффузии в аустените от концентрации углерода с использованием следующего аналитического соотношения [77]: d AC =0.28510-11+0.39410-11 cCA , м2/с. Для оценки количества конечных элементов, необходимых для аппроксимации отдельного зерна [19], определим диффузионный путь атома углерода за время рассматриваемого процесса (500 с) в рамках теории случайных блужданий. Примем, что коэффициент диффузии равен d AC =210-12 м2/с, длина скачка равна =3А, параметр для кубической решетки равен 1/6, тогда диффузионный путь атома углерода за время рассматриваемого процесса составит xдиф =7.7410-5 м. Средний размер зерна рассматриваемой стали (порядка 20010-6 м) превышает диффузионный путь более чем в два раза, поэтому зерно необходимо аппроксимировать несколькими конечными элементами. Для дискретизации рассматриваемой области используются кубичные четырехугольные элементы, внутри которых градиент концентрации не постоянен. Каждое зерно аппроксимируется тремя конечными элементами. Количество элементов было выбрано на основании рекомендаций, представленных в работе [102], и условия приемлемости времени счета и затрачиваемой памяти. Устойчивость численных расчетов обеспечивалась выбором соответствующего шага по времени. Все параметры модели, необходимые для описания процессов деформирования с учетом ферритного превращения [65, 105], приведены в таблице 6. 116 Таблица 6 Параметры модели Аустенит Компоненты тензора упругих свойств, ГПа Параметр скоростной чувствительности Скорость сдвига при напряжении, равном критическому, с-1 Начальный предел текучести, МПа Параметр A Модули упрочнения aii A , aki A A A A п1111 154.0, п1122 122.0, п1212 77 mсA 0.02 0 A 103 cA0 189 À 3.496 105 i aiAi 3.849 102 , akA 4.811102 Параметр BA , 1 с BA =101 Параметр m1A mA 6.036 Параметр ˆc A , МПа ˆcA 90.240 Энергия активации QA , кДж моль QA 93.587 Феррит F F F Компоненты тензора упругих п1111 195.0, п1122 126.0, п1212 102.0 свойств, ГПа (в базисе, связанном с собственной решеткой) Параметр скоростной чувствиmсF 0.02 тельности Скорость сдвига при напряжении, 0 F 103 равном критическому, с-1 Начальный предел текучести, МПа сF 0 154 Параметр F F 2.897 105 Модули упрочнения aii F , aki F i aiFi 3.420 102 , akF 4.275 102 Параметр BF , 1 с BF =0.788 101 Параметр mF Параметр ˆc F , МПа m1 F 6.036 ˆcF 103.425 Энергия активации QF , кДж моль QF 96.814 Материал с кубической решеткой имеет три взаимно ортогональные оси симметрии четвертого порядка [58], совпадающие с кристаллографическими осями. С учетом всех симметрийных и анизотропных свойств тензор линейно-упругих свойств п имеет четыре независимые компоненты, в качестве которых выбираются компоненты с наименьшими значениями индексов в указанных кристаллографических осях: п1111 , п1122 , п1212 , п1221 . В несиммет117 ричном тензоре упругих свойств аустенита и феррита рассматривалось отклонение компонент 1212 и 1221 от их среднего значения для симметричного случая: значение компонент 1212 были увеличены на 5%, а значения компонент 1221 на 5% были уменьшены. Сравнение результатов натурного эксперимента и кривой, которая была получена в ходе решения задачи оптимизации, представлены на рисунках 31, 33. На рисунке 32 приведена зависимость доли образовавшегося феррита от интенсивности деформаций [87], используемая при идентификации параметров закона упрочнения для феррита. Рис. 31. Кривая «интенсивность напряжений–интенсивность накопленных деформаций» для стали, полученная при одноосном сжатии образца со скоростью деформирования 310-3 с-1 при температуре 800 оС ( численный расчет, эксперимент) Рис. 32. Зависимость доли образующегося феррита от интенсивности накопленных деформаций, полученная при одноосном сжатии образца со скоростью деформирования 310-3 с-1 при температуре 760 оС 118 Рис. 33. Кривая «интенсивность напряжений–интенсивность деформаций» для стали, полученная при односном сжатии образца со скоростью деформирования 310-3 с-1 при температуре 760 оС ( численный расчет, эксперимент) На рисунках 34 и 35 приведены кривая «интенсивность напряжений– интенсивность накопленных деформаций» и зависимость объемной доли образовавшегося феррита от интенсивности накопленных деформаций. Рис. 34. Кривая «интенсивность напряжений–интенсивность накопленных деформаций» для стали, полученная при одноосном сжатии образца со скоростью деформирования 310-4 с-1 при температуре 760 оС ( численный расчет, эксперимент) 119 Рис. 35. Зависимость доли образующегося феррита от интенсивности накопленных деформаций, полученная при одноосном сжатии образца со скоростью деформирования 310-4 с-1 при температуре 760 оС (точки соответствуют экспериментальным данным) Таким образом, были рассмотрены вопросы идентификации и верификации модели. На основе данных натурного эксперимента в случае ферритного превращения, происходящего при внешнем механическом воздействии при высокой температуре, была проверена ее адекватность. При этом соответствие между результатами расчета и данными натурного эксперимента можно считать удовлетворительным. 120 ЗАКЛЮЧЕНИЕ В диссертационной работе рассмотрены вопросы, связанные с построением математической модели поведения сталей, описывающей состояние и эволюцию структуры материала с учетом твердотельных фазовых превращений, с использованием несимметричных мер напряженного и деформированного состояния. Целью работы являлась разработка, исследование и реализация математической модели для описания поведения сталей при термомеханическом воздействии с учетом фазовых превращений, которая позволяла бы качественно и количественно адекватно описывать изменение мезо- и микроструктуры материала, а также физико-механических характеристик. Основные результаты диссертационной работы можно сформулировать следующим образом: 1. Разработана двухуровневая математическая модель для описания поведения сталей при термомеханических воздействиях с учетом фазовых превращений, базирующаяся на использовании многоуровневого моделирования, подхода к построению ОС, в основе которого лежит использование в структуре модели на каждом из рассматриваемых масштабных уровней параметров, называемых внутренними переменными, описывающих микроструктуру материала, и являющихся носителями информации о предыстории воздействия. На мезоуровне используется несимметричная упруговязкопластическая физическая теория. 2. Реализован подход по определению явных внутренних переменных на каждом из рассматриваемых масштабных уровней, обеспечивающий согласование определяющих соотношений различных уровней. 3. Предложен способ модификации закона упрочнения систем скольжения, учитывающей дополнительное упрочнение за счет фазового превращения. 4. Разработан программный комплекс, позволяющей проводить вычислительные эксперименты с разработанной моделью в различных условиях термомеханического нагружения. 121 5. Реализован алгоритм проверки адекватности математической модели на основе данных натурного эксперимента; результаты моделирования удовлетворительно согласуются с известными теоретическими и экспериментальными данными. Все этапы построения математической модели в соответствии с поставленной целью выполнены. 122 Литература 1. Башнин Ю. А., Ушаков Б. К., Секей А. Г. Технология термической об- работки стали. – М.: Металлургия. 1986. – 424 с. 2. Билби Б. А., Христиан И. В. Мартенситные превращения//Успехи фи- зических наук. – 1960. – Т. LXX (вып. 3). – С. 515-564. 3. Блантер М. Е. Теория термической обработки. – М.: Металлургия. 1984. – 328 с. 4. Волегов П. С., Никитюк А. С., Трусов П. В. Несимметричные меры на- пряженного и деформированного состояния в физических теориях пластичности: геометрическое обоснование // Неравновесные переходы в сплошных средах: Сб. тр. Всерос. конф. – Пермь: ПГУ. – 2009. – С. 72–75. 5. Волегов П.С., Никитюк А.С., Янц А.Ю. Геометрия поверхности теку- чести и законы упрочнения в физических теориях пластичности // «Вестник ПГТУ», Серия «Математическое моделирование систем и процессов». Пермь: Изд-во ПГТУ, 2009. - N17. - С. 25-33. 6. Георгиева И. Я., Изотов В. И., Панкова Н. Н. Структурные и кристал- логеометрические особенности изотермического мартенсита в сплаве Fe – 24% Ni – 3% Mn // ФММ. – 1971. – Т. 32. – Вып. 3. – С. 626 – 631. 7. Гринфельд М. А. Методы механики сплошных сред в теории фазовых превращений. – М.: Наука. Гл. ред. физ.-мат. лит., 1990. – 312 с. 8. Гудцов Н. Т., Курдюмов Г. В., Селяков Н. Я. Рентгенографическое ис- следование структуры углеродистой стали // Журнал прикладной физики. — 1927. — Т. 4. – Вып. 2. – С. 51–82. 9. Гузовская М. А., Гуляев А. П. Изучение образования видманштетовой структуры // Изв. АН СССР. Металлы. – 1967. – №1. – С. 112 – 115. 10. Гуляев А. П. Термическая обработка стали. – М.: Машгиз. 1960. – 496 с. 123 11. Данков П. Д. Механизм фазового превращения с точки зрения принци- па ориентационного и размерного соответствия // Известия сектора физико– химического анализа АН СССР . – 1943. – Т. 16. – № 1. – С. 82 – 95. 12. Де Грот С. Р. Термодинамика необратимых процессов. – М.: Гос. изд. технико–теоретической литературы. 1956. – 281 с. 13. Иванов Д. А., Куваев Н. В., Куваева Т. В. Расчет теплоемкости низко- углеродистой низколегированной стали при моделировании неизотермических фазовых превращений //Теория и практика металлургии. – 2010. – Т. 1. – Вып. 2. – С. 43–48. 14. Изотов В. И. Морфология и кристаллогеометрия реечного мартенсита // ФММ. – 1972. – Т. 34. – Вып. 1. – С. 123 – 132. 15. Исайчев И. В. Ориентация цементита в отпущенной углеродистой ста- ли // ЖТФ. – 1947. – Т. 17. – Вып. 6. – С. 835–838. 16. Исупова И. Л., Трусов П. В. Математическое моделирование фазовых превращений в сталях при термомеханической нагрузке // Вестник ПНИПУ. Механика. – 2013. – № 3.– с. 126-156. 17. Исупова И.Л., Трусов П.В. Обзор математических моделей для описа- ния фазовых превращений в сталях// Вестник ПНИПУ. Механика. – 2013. – №3.– с. 157-191. 18. Исупова И. Л., Трусов П. В. Двухуровневая модель для описания пове- дения сталей при термомеханическом нагружении с учетом мартенситных превращений: алгоритм реализации модели // Вычислительная механика сплошных сред. – 2013. – Т. 6. – № 4. – С. 491-503. 19. Исупова И. Л., Трусов П. В. Моделирование поведения сталей с учетом диффузионных фазовых превращений // Научно-технические ведомости СПбГПУ. – 2014. – № 1(190). – С. 191 – 197. 20. Кащенко М. П., Чащина В. Г. Динамическая теория мартенситно- го превращения в сплавах железа и решение проблемы критического размера зерна. – М.–Ижевск: НИЦ «Регулярная и хаотическая динамика», Ижевский институт компьютерных исследований, 2010. – 132 с. 124 21. Кащенко М. П., Чащина В. Г. Формирование мартенситных кристаллов в предельном случае сверхзвуковой скорости роста //Письма о материалах. – 2011.– Т.1. – С. 7–14. 22. Кидин И. Н., Штремель М. А., Лизунов В. И. Сдвиговой механизм по- лиморфного превращения при нагреве отожженного хромистого железа // ФММ. – 1966. – Т. 21. – № 4. – С. 586 – 594. 23. Коган Л. И., Энтин Р. И. Кинетика полиморфного превращения железа // ДАН СССР. – 1950. – Т. 73. – Вып. 6. – С. 1173 – 1176. 24. Конобеевский С. Т. К теории фазовых превращений // Журнал экспе- риментальной и теоретической физики. – 1943. – Т. 13. – Вып. 6. – С. 185 – 214. 25. Курдюмов Г. В. Термическая обработка стали в свете рентгенографи- ческих исследований // Вестник металлопромышленности. – 1932. – №9. – C. 20–34. 26. Курдюмов Г. В. Явления закалки и отпуска в стали. – М.: «Металлург- издат». 1960. – 64 с. 27. Курдюмов Г. В., Утевский Л. М., Энтин Р. И. Превращения в железе и стали. – М.: «Наука». 1977. – 236 с. 28. Лебедев В. Г., Данилов Д. А., Галенко П. К. Об уравнениях модели фа- зового поля для неизотермической кинетики превращений в многокомпонентной и многофазной системе //Вестник Удмуртского университета. Физика и химия. – 2010. – Вып. 1. – С. 26 –33. 29. Леонтьев Б. А., Зубарев Б. Ф., Матвеева М. И., Шелягина Т. И. Иссле- дование поверхности микрорельефа стали с видманштетовой структурой // Изв. АН СССР. Металлы. – 1967. – №1. – С. 116 – 121. 30. Лурье А.И. Нелинейная теория упругости. М.: – Наука. 1980. 512 с. 31. Металловедение и термическая обработка стали: Справочник / Под. ред. М. Л. Бернштейна, А. Г. Рахштада. – М.: Металлургия – Т. II. Основы термической обработки. – 1983. – 368 с. 125 32. Мовчан А. А., Мовчан И. А. Одномерная микромеханическая модель нелинейного деформирования сплавов с памятью формы при прямом и обратном термоупругих превращениях //Механика композиционных материалов и конструкций. – 2007. – Т.13. – № 3. – C. 297–322. 33. Мовчан А. А., Мовчан И. А., Сильченко Л. Г. Микромеханическая мо- дель нелинейного деформирования сплавов с памятью формы при фазовых и структурных превращениях //Известия Российской академии наук. Механика твердого тела. – 2010. – № 3. – C. 118–130. 34. Новиков И. И. Теория термической обработки металлов. – М.: Метал- лургия. 1986. – 480 с. 35. Пикеринг Ф. Б. Физическое металловедение и разработка сталей. – М.: Металлургия. 1982. – 184 с. 36. Поздеев А. А., Трусов П. В., Няшин Ю. И. Большие упруго- пластические деформации: теория, алгоритмы, приложения. – М.: Наука. 1986. – 232 с. 37. Потак Я. М. Высокопрочные стали. – М.: Металлургия. 1972. – 208 с. 38. Пригожин И., Кондепуди Д. Современная термодинамика. От тепловых двигателей до диссипативных структур: Пер. с англ. Ю. А. Данилова и В. В. Белого – М.: Мир, 2002. – 461 с. 39. Рыбин В.В. Большие пластические деформации и разрушение метал- лов. – М.: Металлургия. – 1986. 224 с. 40. Садовский В. Д. Структурная наследственность в стали – М.: Метал- лургия. 1973. – 205 с. 41. Садовский В. Д. Структурные превращения при закалке и отпуске ста- лей. Свердловск УФАН СССР. 1945. – 72 с. 42. Смиренская Н. А., Козлова А. Г., Энтин Р. И. Мартенситоподобная ре- акция в малоуглеродистых сталях // ФММ. – 1979. – Т. 47. – Вып. 2. – С. 368 – 379. 126 43. Смирнов М. А., Счастливцев В. М., Журавлев Л. Г. Основы термиче- ской обработки стали: Учебное пособие. – Екатеринбург: УрО РАН.1999. – 496 с. 44. Счастливцев В. М., Копцева В. М. Электронно-микроскопическое ис- следование образования аустенита при нагреве конструкционной стали // ФММ. – 1976. – Т. 42. – № 4. – С. 837 – 847. 45. Сухомлин Г. Д. Электронномикродифракционное исследование ориен- тационных соотношений феррит-цементит // ФММ. – 1974. – Т. 38. – Вып. 4. – С. 878–881. 46. Трусов П. В., Ашихмин В. Н., Волегов П. С., Швейкин А. И. Конститу- тивные соотношения и их применение для описания эволюции микроструктуры // Физическая мезомеханика. – 2009. – Т.12. – №3. – С. 61-71. 47. Трусов П. В., Ашихмин В. Н., Швейкин А. И. Двухуровневая модель упругопластического деформирования поликристаллических материалов // Механика композиционных материалов и конструкций. – 2009. – Т.15. – №3. – С. 327-344. 48. Трусов П. В., Волегов П. С., Янц А. Ю. Несимметричная физическая теория пластичности для описания эволюции микроструктуры поликристалла// Физическая мезомеханика. – 2011. –Т. 14. – № 1. – С. 19-31. 49. Трусов П. В., Исупова И. Л. Построение двухуровневой модели для описания поведения сталей при термомеханическом нагружении в интервале мартенситных превращений // Физическая мезомеханика. 2014. – Т. 17. – № 2. – С. 13-25. 50. Трусов П. В., Нечаева Е. С., Швейкин А. И. Применение несимметрич- ных мер напряженного и деформированного состояния при построении многоуровневых конститутивных моделей материалов// Физическая мезомеханика. – 2013. –Т. 16. – № 2. – С. 15-31. 51. Трусов П. В., Швейкин А. И. Многоуровневые физические модели мо- но- и поликристаллов. Статистические модели // Физическая мезомеханика. – 2011. – № 4. – С. 17-28. 127 52. Трусов П. В., Швейкин А. И. Многоуровневые физические модели мо- но- и поликристаллов. Прямые модели // Физическая мезомеханика. – 2011. – Т. 14. – № 4. – С. 5-30. 53. Трусов П. В., Швейкин А. И. Теория пластичности. – Пермь: Изд-во ПНИПУ. – 2011. – 419 с. 54. Трусов П. В., Швейкин А. И., Нечаева Е. С., Волегов П. С. Многоуров- невые модели неупругого деформирования материалов и их применение для описания эволюции внутренней структуры // Физическая мезомеханика. – 2012. – Т.15. – №1. – С. 33-56. 55. Тушинский Л. И., Батаев А. А., Тихомирова Л. Б. Структура перлита и конструктивная прочность стали. – Новосибирск: ВО «Наука». 1993. – 280 с. 56. Утевский Л. М., Панкова М. Н. Электронно – микроскопическое иссле- дование кристаллогеометрии мартенситного перехода // Металлофизика. – 1979. – Т. 1. – №2. – С. 66 – 85. 57. Фрейдин А. Б., Шарипова Л. Л. Равновесные двухфазные деформации и зоны фазовых переходов в приближении малых деформаций//Изв. вузов. Северо-Кавказский регион. Естеств. науки. Нелинейные проблемы механики сплошных сред. Спецвыпуск. – 2003. – С. 291-298. 58. Черных К. Ф. Введение в анизотропную упругость. – М.: Наука. Гл. ред. физ.-мат. лит., 1988. – 190 с. 59. Штейнберг С. С. Избранные статьи. – М.: «Машгиз». 1950. – 255 с. 60. Энтин Р. И. Превращение аустенита в стали. – М.: Металлургия, 1960. – 252 с. 61. Этерашвили Т. В., Утевский Л. М., Спасский М. Н. Строение пакетного мартенсита, локализация остаточного аустенита в конструкционной стали // ФММ. – 1979. – Т. 48. – Вып. 4. – С. 807–815. 62. Artemev A., Jin Y., Khachaturyan A. Three-dimensional phase field model and simulation of cubic tetragonal martensitic transformation in polycrystals // Phil. Mag. – 2002. – Vol. 82. – P. 1249 – 1270. 128 63. Artemev A., Jin Y., Khachaturyan A. Three-dimensional phase field model of proper martensitic transformation // Acta Mater. – 2001. – Vol. 49. – P. 1165 – 1177. 64. Avrami, M. Kinetics of phase change. II: Transformation–time relations for random distribution of nuclei // Journal of Chemical Physics. – 1940. – Vol. 8. – P. 212. 65. Barbe F., Quey R. A numerical modelling of 3D polycrystal-to-polycrystal diffusive phase transformation involving crystal plasticity// Int. Journal of Plasticity. – 2011. – Vol. 27. – Р.823–840. 66. Barbe F., Quey R., Taleb L. Numerical modelling of the plasticity induced during diffusive transformation. Case of a cubic array of nuclei// Europ. J. Mechanics A/ Solids. – 2007. – Vol. 26. – Р.611–625. 67. Beese A. M. Experimental investigation and constitutive modeling of the large deformation behavior of anisotropic steel sheets undergoing strain-induced phase transformation. PhD thesis, Massachusetts Institute of Technology, 2011. 146 pp. 68. Cahn J. W., Hilliard J. E. Free energy of a non-uniform systems. I. Interfacial free energy // J. Chem. Phys. – 1958. – Vol. 28. – P. 258 – 266. 69. Chen L.-Q., Khachaturyan A. Computer simulation of structural transformations during precipitation of an ordered intermetallic phase //Acta Mater. – 1991. – Vol. 39 – P. 2533–2551. 70. Cherkaoui M., Berveiller M., Sabar H. Micromechanical modeling of martensitic transformation induced plasticity (trip) in austenitic single crystals// Int. J. Plasticity. – 1998. – Vol. 14.– No.7. – Р.597–626. 71. Cho J.-Y. Finite element modeling of martensitic phase transformation. PhD thesis, Texas Tech University, 2009. 109 pp. 72. Chuang Y. –Y., Chang Y. A. A Thermodynamic Analysis and Calculation of the Fe-Ni-Cr Phase Diagram // Metall. Mater. Trans. – 1987. – Vol. 18A. – P. 733745. 129 73. De Oliviera W. P., Savi M. A., Pacheco P. M. C. L., De Souza L. F. G. Thermomechanical analysis of steel cylinders quenching using a constitutive model with diffusional and non-diffusional phase transformations // Mechanics of Materials. – 2010. – Vol. 42. – P. 31–43. 74. Dinsdale A. T. SGTE Data for Pure Elements // Calphad. – 1991. –Vol. 15. – P. 317 – 425. 75. Dippenaar R. J., Honeycombe R. W. K. The crystallography and nucleation of pearlite // Proc. R. Soc. London A. – 1973. – Vol. 333. – P. 455–475. 76. Fischlschweiger M., Cailletaud G., Antretter T.A mean-field model for transformation induced plasticity including backstress effects for non-proportional loadings// Int. J. Plasticity. – 2012. – Vol. 37. – Р.53–71. 77. Gegner J. Concentration- and temperature-dependent diffusion coefficient of carbon in FCC iron mathematically derived from literature data // Proceedings of IV Int. Conf. «Mathematical Modeling and Computer Simulation of Materials Technologies», Ariel, Israel, 2006. – P. 158 – 167. 78. Habraken A. M. Modeling the plastic anisotropy of metals // Arch. Meth. Engng. – 2004. – Vol. 11.– No.1. – Р.3–96. 79. Han G., Yuan H. Deformation and damage evolution of austenitic steel AISI 304 with martensite phase transformation // Proceedings of 13th International Conference on fracture, Beijng, China, 2013. – P. 1–11. 80. Hoffmann W., Schumacher G. // Archiv. f. Eisen nuttenwesen. – 1958. – Bd. 26. – №2. – S. 99 – 104. 81. Hömberg D., Sokolowski J. Optimal control of laser hardening // Adv. Math. Sci. – 1998. – Vol. 8. – Р.911–928. 82. Koistinen D.P., Marburger R.E. A general equation prescribing the extent of the austenite-martensite transformation in pure ironcarbon alloys and plain carbon steels // Acta Metallurgica. – 1959. – Vol. 7. – P. 59–60. 83. Kouznetsova V.G., Geers M.G.D. A multi-scale model of martensitic transformation plasticity// Mechanics of Materials. – 2008. – Vol. 40. – Р. 641– 657. 130 84. Kelly P., Nutting J. Martensitic transformation in carbon steels // Proc. Roy. Soc. – 1960. – A 259. – № 296. – P. 45–48. 85. Kurdjumow G., Sachs G. Uber den Mechanismus der Stahlhartung // Z. Phys. – 1930. – Bd. 64. – S. 325–343. 86. Lee M.-G., Kim S.-J., Han H.N. Crystal plasticity finite element modeling of mechanically induced martensitic transformation (MIMT) in metastable austenite// Int. J. Plasticity. – 2010. – Vol. 26. – Р.688–710. 87. Lewis J. R. Formation of deformation induced ferrite during mechanical testing. A thesis for the Degree of Master of Engineering, McGill University, Montreal, Canada, 1996. 113 p. 88. Li Y. Fatigue crack initiation (in 304L steel): influence of the microstructure and variable amplitude loading. PhD thesis, Centrale Paris, 2012. 181 pp. 89. Logé R.E., Chastel Y.B. Coupling the thermal and mechanical fields to metallurgical evolutions within a finite element description of a forming process// Comput. Methods Appl. Mech. Engrg. – 2006. – Vol.195. – Р. 6843–6857. 90. Loginova I., Agren J., Amberg G. On the formation of Widmanstaten ferrite in binary Fe-C phase-field approach // Acta. Materialia. – 2004. – Vol. 52. – P. 4055–4063. 91. Loginova I., Amberg G., Agren J. Phase-field simulations of non- isothermaly binary alloy solidification // Acta. Materialia. – 2001. – Vol. 49. – P. 573–581. 92. Loginova I., Odqvist J., Amberg G., Agren J. The Phase-field approach and solute drag modeling of the transition to massive transformation in binary Fe-C alloys // Acta. Mater. – 2003. – Vol. 51. – P. 1327–1339. 93. Mahnten R., Schneidt A., Antretter T. Macro modeling and homogenization for transformation induced plasticity of a low-alloy steel // International Journal of Plasticity. – 2009. – Vol. 25. – P. 183–204. 94. Massalski T. The mode and morphology of massive transformations in Cu- Ga, Cu-Zn, Cu-Zn-Ga, Cu-Ga-Ge alloys // Acta Metallurg. – 1958. – Vol. 6. – P. 242–253. 131 95. Miettinen J. Calculation of solidification-related thermophysical properties for steels // Metall. Mater. Trans B. –1997. –Vol. 28A. – P. 281 – 297. 96. Nishiyama Z. X-ray investigation of the mechanism of transformation from face-centered cubic lattice to body-centered cubic// Sci. Rep. Tohoku Imp. Univ. – 1934. – Vol. 23. – P. 637–664. 97. Olson G.B., Cohen M. Kinetics of strain-induced martensitic nucleation// Metallurgical Transactions A. – 1975. – Vol.6A. – Р.791–795. 98. Ozdemir I., Brekelmans W.A.M., and Geers M.G.D. Computational homogenization for heat conduction in heterogeneous solids // International Journal for Numerical Methods in Engineering. – 2008. – Vol. 73. – No. 2. – P.185 – 204. 99. Pitsh W. Der Orientierungszusammenhang Zwishen Zementit und Austenit // Acta Metallurg. – 1962. – Vol. 10. – № 9. – P. 897–898. 100. Redlich O., Kister A. T. Algebraic representation of thermodynamic properties and the classification solutions // Ind. Eng. Chem. – 1948. – Vol. 40. – № 2. – P. 345 – 348. 101. Rodriguez-Martinez J. A., Pesci R., Rusinek A. Experimental study on the martensitic transformation in AISI 304 steel sheets subjected to tension under wide ranges of strain rate at room temperature // Materials Science and Engineering: A. – 2011. – Vol. 528. – № 18. – P. 5974 – 5982. 102. Segal Ir. A. Finite element methods for the incompressible Navier-Stokes equations. – Institute of Applied Mathematics, Delft, Netherlands, 2012. – 80 p. 103. Steinbach I., Apel M. Multi-phase field model for solid state transformation with elastic strain // Physica D. – 2006. – Vol. 217. – P. 153 – 160. 104. Taylor G.I. Plastic strain in metals// J. Inst. Metals. – 1938. – Vol.62. – Pp.307–324. 105. Tjahjanto D. D., Turteltaub S., Suiker A. S. J. Crystallographically based model for transformation-induced plasticity in multiphase carbon steels // Continuum Mech. Thermodyn. – 2008. – Vol. 19. – P. 399 – 422. 132 106. Tomita, Y., Shibutani, Y. Estimation of deformation behavior of TRIP steels-smooth/ringed-notched specimens under monotonic and cyclic loading // Int. J. Plast. – 2000. – Vol. 16. – P. 769 – 789. 107. Trusov P.V., Volegov P.S., Shveykin A.I. Multilevel model of inelastic deformation of FCC polycrystaline with description of structure //Computational Materials Science. – 2013. – Vol. 79. – P. 429 – 441. 108. Turteltaub S., Suiker A.S.J. A multiscale thermomechanical model for cubic to tetragonal martensitic phase transformations// Int. J. Solids and Structures. – 2005. – doi:10.1016/j.ijsolstr.2005.06.065. 109. Wagemaker M., Mulder F. M., Van der Ven A. The role of surface and interface energy on phase stability of nanosized insertion compounds // Adv. Mater. – 2009. – Vol. 21. – P. 2703 – 2709. 110. Wang, J.J., van der Zwaag, S. Stabilization mechanisms of retained austenite in transformation-induced plasticity steel// Metall. Mater. Trans. A. – 2001. – Vol. 32.– № 6. – P. 1527–1539. 111. Wang Y., Khachaturyan A. Three-dimensional phase field model and computer modeling of martensitic transformations // Acta Mater. – 1997. – Vol. 45. – P. 759 – 773. 112. Wever F. Zur Frage der Stahlhärtung, besonders zur Kinetik der Umwandlungen// Stahl und Eisen. – 1949. – Bd. 69. – №19. – S. 664 – 670. 113. Yadegari S., Turteltaub S., Suiker A. S. J. Coupled thermomechanical analysis of transformation-induced plasticity in multiphase steels // Mechanics of Materials. – 2012. – Vol. 53. – P. 1 – 14. 114. Yamanaka A., Takaki T., Tomita Y., Yoshino M. Crystal plasticity phasefield simulation of deformation behavior and microstructure evolution in polycrystalline material //Proceedings of X International Conference on Computional Plasticity. COMPLAS X (CD-ROM), Barcelona, Spain, 2009. – Vol. 462. – P. 1–4. 115. Zaera R., Rodriguez-Martinez J. A., Casado A., Fernandez-Saez J., Rusinek A., Pesci R. A constitutive model for analyzing martensite formation in austenitic 133 steels deforming at high strain rates // International Journal of Plasticity. – 2012. – Vol. 29. – P. 77 – 101. 116. www.thermocalc.com 134