алгоритмы построения выпуклых оболочек и их применение
advertisement

Министерство науки и образования Российской Федерации
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Факультет информатики
Кафедра теоретических основ информатики
УДК 681.03
ДОПУСТИТЬ К ЗАЩИТЕ В ГАК
Зав. кафедрой, д.т.н., проф.
__________ Костюк Ю. Л.
«___»____________ 2004 г.
Чаднов Роман Витальевич
АЛГОРИТМЫ ПОСТРОЕНИЯ ВЫПУКЛЫХ
ОБОЛОЧЕК И ИХ ПРИМЕНЕНИЕ В ГИС И САПР
Дипломная работа
Научный руководитель,
профессор кафедры ТОИ, д.т.н., доцент
А.В. Скворцов
Исполнитель,
студ. гр. 1491
Р.В. Чаднов
Электронная версия дипломной работы помещена
в электронную библиотеку. Файл
Администратор
Томск – 2004
Реферат
Дипломная работа 61 с., 49 рис., 17 источников.
ВЫПУКЛЫЕ ОБОЛОЧКИ, ТРИАНГУЛЯЦИЯ ДЕЛОНЕ, ВЫЧИСЛИТЕЛЬНАЯ
ГЕОМЕТРИЯ, КОМПЬЮТЕРНАЯ ГРАФИКА, ГЕОИНФОРМАЦИОННЫЕ СИСТЕМЫ,
СИСТЕМЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ, ВЫЧИСЛИТЕЛЬНЫЙ
ЭКСПЕРИМЕНТ
Объект исследования – алгоритмы построения выпуклых оболочек на плоскости и в
трехмерном пространстве.
Цель работы – анализ и исследование известных алгоритмов построения выпуклых
оболочек с целью определения наиболее продуктивных алгоритмов для применения на практике; разработка эффективных алгоритмов построения выпуклых оболочек; исследование
возможностей применения алгоритмов построения выпуклых оболочек в трехмерном пространстве для построения триангуляции Делоне.
Метод исследования – экспериментальный.
Результаты работы – описаны широко известные и новые алгоритмы построения выпуклых оболочек в двух- и трехмерном пространствах, исследована их производительность и
возможность практического применения. Описан комбинированный алгоритм построения
выпуклой оболочки на плоскости, устойчивый к типу распределения исходных данных.
Степень внедрения – разработана библиотека алгоритмов построения выпуклой оболочки на плоскости и в пространстве, которая может быть применена в различных приложениях. В настоящее время разработанная библиотека используется в коммерческой геоинформационной системе IndorGIS 5.0 для построения выпуклых оболочек на плоскости.
Прогноз о развитии исследования – автором планируется продолжение исследования
и разработки эффективных алгоритмов вычислительной геометрии. В ближайшее время автор планирует заняться разработкой алгоритмов построения выпуклой оболочки в трехмерном пространстве, а также применением этих алгоритмов для построения триангуляции с
ограничениями.
2
Содержание
Введение ........................................................................................................................................ 4
1 Определения и постановка задачи ........................................................................................... 5
1.1 Задача построения выпуклой оболочки ........................................................................ 5
1.2 Трудоемкость алгоритмов построения выпуклой оболочки....................................... 6
1.3 Количество граней выпуклой оболочки........................................................................ 6
2 Обзор алгоритмов ...................................................................................................................... 7
2.1 Алгоритмы построения выпуклых оболочек в двухмерном пространстве ............... 7
2.1.1 Алгоритм обхода Джарвиса (Jarvis march) ........................................................... 7
2.1.2 Алгоритм обхода Грэхема (Graham Scan) ............................................................. 9
2.1.3 Алгоритм монотонных цепочек Эндрю (Monotone Chain) ................................ 10
2.1.4 Алгоритм типа «Разделяй и властвуй» (Divide and conquer) ............................. 12
2.1.5 Алгоритм «быстрого построения» (QuickHull).................................................. 13
2.1.6 Алгоритм Чена ....................................................................................................... 14
2.2 Особенности практической реализации алгоритмов построения выпуклой оболочки
на плоскости......................................................................................................................... 18
2.2.1 Практические особенности сравнения углов ...................................................... 18
2.2.2 Иерархическое представление выпуклых оболочек. Практические особенности
реализации алгоритма Чена. .......................................................................................... 20
2.3 Алгоритмы построения выпуклых оболочек в трехмерном пространстве ............ 22
2.3.1 Алгоритм «грубой силы» ...................................................................................... 22
2.3.2 Алгоритм «заворачивания подарка» .................................................................... 22
2.3.3 Алгоритм «разделяй и властвуй» ......................................................................... 23
2.4 Обзор областей применения......................................................................................... 24
2.4.1 В ГИС и САПР ....................................................................................................... 24
2.4.2 Другие области ....................................................................................................... 24
2.5 Существующие проблемы в области разработки алгоритмов построения выпуклых
оболочек ............................................................................................................................... 24
3 Модификации алгоритмов ...................................................................................................... 26
3.1 Модификации алгоритмов на плоскости .................................................................... 26
3.1.1 Отсечение восьмиугольником .............................................................................. 26
3.1.2 Отсечение прямоугольником ................................................................................ 27
3.1.3 Модифицированный алгоритм Чена .................................................................... 28
3.2 Модификация алгоритмов в пространстве............................................................... 30
4 Исследование алгоритмов на плоскости ............................................................................... 31
4.1 Методика исследования................................................................................................ 31
4.2 Результаты исследования ............................................................................................. 32
4.2.1 Равномерное распределение точек....................................................................... 32
4.2.2 Нормальное распределение точек ........................................................................ 33
4.2.3 Лапласовское распределение точек...................................................................... 34
4.2.4 Распределение точек на окружности ................................................................... 35
4.2.5 Кластерное распределение точек ......................................................................... 36
4.3 Анализ результатов ....................................................................................................... 37
4.4 Комбинированный алгоритм........................................................................................ 37
5 Практическое применение алгоритмов построения выпуклых оболочек.......................... 43
5.1 Применение алгоритмов построения выпуклой оболочки на плоскости ................ 43
5.2 Практическое применение алгоритмов построения выпуклой оболочки в
пространстве ........................................................................................................................ 44
Заключение .................................................................................................................................. 46
Список использованных источников ........................................................................................ 47
3
Введение
Вычислительная геометрия [1,2] занимается изучением разработки и исследования алгоритмов для решения геометрических проблем. Задача построения выпуклых оболочек, является одной из центральных задач вычислительной геометрии. Важность этой задачи происходит не только из-за огромного количества приложений (в распознавании образов, обработке изображений, базах данных, в задаче раскроя и компоновки материалов, математической статистике), но также и из-за полезности выпуклой оболочки как инструмента решения
множества задач вычислительной геометрии.
Эта задача позволяет разрешить целый ряд других, иногда с первого взгляда не связанных с ней вопросов: построение диаграмм Вороного, построение триангуляций и т.д. Построение выпуклой оболочки конечного множества точек на плоскости довольно широко исследовано и имеет множество приложений. Очень широко алгоритмы построения выпуклой
оболочки используются в геонформатике и геоинформационных системах.
Задача построения выпуклой оболочки имеет давнюю историю. Она является одной из
первых задач вычислительной геометрии, с которой начала зарождаться эта наука. В настоящее время известно достаточно большое число алгоритмов построения выпуклой оболочки, однако существует проблема, связанная с недостаточным количеством работ, посвященных анализу и/или обзору этих алгоритмов, особенно в трехмерном пространстве. В
данной работе предпринята попытка восполнить этот недостаток.
В главе 1 дано формальное описание задачи построения выпуклой оболочки.
В главе 2 изложены результаты выполненного автором описания и некоторого анализа
наиболее распространенных современных алгоритмов построения выпуклой оболочки, как в
двумерном, так и в трехмерном пространствах.
В главе 3 описаны предложенные автором модификации нескольких существующих алгоритмов, нацеленные на увеличение скорости их работы.
В главе 4 данной работы приведены результаты экспериментального сравнения скорости
работы алгоритмов на различных классах входных данных.
В главе 5 описаны практические результаты работы – внедрение результатов работы в
ГИС и САПР.
4
1 Определения и постановка задачи
1.1 Задача построения выпуклой оболочки
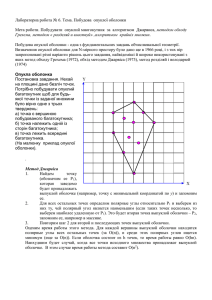
Понятие выпуклой оболочки формально определяется следующим образом [1]:
Определение 1. Выпуклой оболочкой (ВО) множества точек S называется наименьшее
выпуклое множество, содержащее S.
В случае, когда S – конечное множество точек на плоскости, это определение можно
представить наглядно. Предположим, что множество точек охвачено большой растянутой
резиновой лентой. Эта лента имеет форму выпуклой оболочки. (см. рис. 1.)
Однако приведенное выше простое определение выпуклой оболочки неконструктивно.
Для более формального описания необходимо ввести некоторые дополнительные понятия.
Будем рассматривать d-мерное евклидово пространство Ed.
Определение 2. Область F, принадлежащая пространству Ed, будем называть выпуклой,
если для любой пары точек f1 и f2, принадлежащих F, отрезок f1f2 целиком принадлежит D.
Определение 3. Выпуклой оболочкой множества точек S, принадлежащих пространству
Ed, называется граница наименьшей выпуклой области в Ed, которая охватывает S.
Рис. 1. Иллюстрация определения выпуклой оболочки в пространстве Ed
Выпуклая оболочка множества точек S обычно обозначается как CH(S) [1].
Задача построения выпуклой оболочки на плоскости обычно ставится в двух вариантах.
Задача CH1. В Ed задано множество S, содержащее n точек. Требуется определить те из
них, которые являются вершинами выпуклой оболочки CH(S).
Задача CH2. В Ed задано множество S, содержащее n точек. Требуется построить их выпуклую оболочку (т.е. найти полное описание границы CH(S)). Ответом этой задачи является
упорядоченный список граней выпуклой оболочки.
В двумерном случае гранями являются вершины и ребра оболочки. В трехмерном случае
выпуклая оболочка описывается набором граней, ребер, и точек, принадлежащих ей.
Задача CH1 обычно возникает в теории, а на практике она используется редко ввиду низкой практической полезности результатов решения этой задачи.
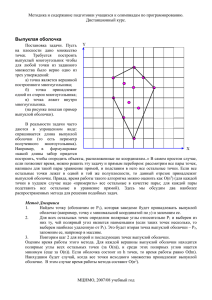
На рис. 2 проиллюстрирован пример задачи построения выпуклой оболочки на плоскости. Множество S состоит из тринадцати точек. Результатом работы алгоритма построения
5
выпуклой оболочки должен быть список (p1, p2, p3, p4, p5, p6). Стоит отметить, что список,
содержащий вершины выпуклой оболочки может начинаться с любой из вершин, входящих
в неё. К примеру, список (p3, p4, p5, p6, p1, p2) тоже является правильным результатом.
Рис. 2. Тринадцать точек, шесть из которых являются
вершинами выпуклой оболочки
Замечание: если pq является ребром выпуклой оболочки множества S, и существует точка
r ∈ S \{p,q}, которая находится на ребре pq, то считается, что точка r не является вершиной
выпуклой оболочки.
1.2 Трудоемкость алгоритмов построения выпуклой оболочки
Сведем задачу сортировки n положительных действительных чисел x1,.., xn к задаче CH2.
Поставим в соответствие числу xi точку (xi, xi2) и присвоим ей номер i. Выпуклая оболочка
этого множества, представленная в стандартном виде будет представлять собой упорядоченное относительно значения абсциссы множество всех точек из исходного. Из него за линейное время можно получить отсортированный список.
Задача сортировки за линейное время сводится к задаче построения выпуклой оболочки,
и, следовательно, трудоемкость нахождения упорядоченной выпуклой оболочки для n точек
на плоскости составляет не менее O(n log n).
1.3 Количество граней выпуклой оболочки
Если в пространстве Ed задано множество S, состоящее из n точек, то сколько граней содержит выпуклая оболочка этого множества? Если размерность пространства равна двум, то,
очевидно, что количество граней не превысит 2n, т.к. выпуклая оболочка S – это многоугольник, состоящий из не более n вершин и n ребер. Для d = 3, используя формулу Эйлера
(V-E+F=2, где V – количество вершин, Е – количество ребер, F – количество граней), можно
определить, что количество ребер и граней линейно соотносится с исходным количеством
точек, так что общее число граней также имеет порядок O(n). Как показано в [3], для более
высоких размерностей, к примеру, для d=4 или d=5 число граней может быть квадратичным,
а для d ≥ 6 это число имеет порядок O( n d / 2 ).
6
2 Обзор алгоритмов
2.1 Алгоритмы построения выпуклых оболочек в двухмерном пространстве
2.1.1 Алгоритм обхода Джарвиса (Jarvis march)
Этот алгоритм, предложенный Джарвисом в 1973 в [4], очень легок для понимания. Он
также известен под названием «метод заворачивания подарка», так как этот алгоритм обрабатывает точки выпуклой оболочки одну за другой, как если бы мы оборачивали множество
точек листом бумаги. Джарвис обратил внимание на то, что многоугольник, которым является выпуклая оболочка, с одинаковым успехом можно задать упорядоченным множеством,
как его ребер, так и его вершин. Если задано множество точек, то довольно трудно быстро
определить, является или нет некоторая точка крайней. Однако если даны две точки, то непосредственно можно проверить, является или нет соединяющий их отрезок ребром выпуклой оболочки.
Алгоритм начинает свою работу с нахождения точки p1 из S, которая гарантированно является вершиной выпуклой оболочки. Обычно за точку p1 берется самая нижняя из точек
множества S. Если S содержит несколько точек с минимальной ординатой, то берется самая
левая из них. Очевидно, что точка p1 может быть найдена за время O(n).
Так как p1 является вершиной выпуклой оболочки, то обязательно должна существовать
такая точка p2, которая также является вершиной выпуклой оболочки, а ребро, соединяющее
эту точку с точкой p1p2, является ребром выпуклой оболочки. Таких точек всегда две. Возьмем точку p2 такой, что ребро p1p2 расположено против часовой стрелки.
Точка p2 находится следующим образом. Пусть l1 – горизонтальная линия, проходящая
через p1. Тогда p2 – первая точка, которой коснется линия l1, если её поворачивать относительно точки p1 против часовой стрелки. Пусть для каждой точки q ∈ S \ {p1} определен угол
αq – угол между l1 и отрезком p1q. Заметим, что 0 ≤ αq < 2π. Следовательно, p2 – это такая
точка из S \ {p1}, для которой этот угол минимален. Если таких точек несколько, то p2 – так
из них, которая наиболее удалена от p1.
Таким образом, имея p1, мы можем найти следующую вершину выпуклой оболочки, рассмотрев все точки q ∈ S \ {p1}, и выбрав из них ту, для которой угол αq минимален. Это
можно сделать за время O(n). Проще говоря, р2 - это точка, имеющая наименьший положительный полярный угол относительно точки p1 как начала координат.
Дальнейший ход алгоритма идет тем же путем. Пусть l2 –линия, проходящая через p1 и
p2. Тогда для каждой точки q ∈ S \ {p2} определим угол αq – угол между l2 и отрезком p2q.
(Теперь αq – это угол, на который мы должны повернуть l2 против часовой стрелки, чтобы
коснуться ею точки q). Тогда p3, следующая вершина выпуклой оболочки – это та точка, чей
α-угол минимален. Следовательно, p3 можно найти за время O(n).
Мы продолжаем нахождение вершин выпуклой оболочки p4, p5, … до тех пор, пока не
вернемся в p1. Алгоритм Джарвиса обходит кругом выпуклую оболочку (отсюда и соответствующее название — обход Джарвиса), порождая в нужном порядке последовательность
вершин выпуклой оболочки, по одной на каждом шаге (рис. 3).Более формально, если
ph+1 = p1, то мы останавливаемся, и можем вывести выпуклую оболочку (p1, p2, ….. , ph). Конец алгоритма. ■
Трудоемкость этого алгоритма составляет O(hn), где h – общее количество вершин, входящих в выпуклую оболочку. Первая вершина p1 находится за время O(n). Имея p1, 2, … pk
7
мы находим следующую вершину выпуклой оболочки за время O(n). Таким образом, общее
время выполнения алгоритма может быть вычислено как
h +1
O ∑ n = O(n ⋅ (h + 1)) = O(n ⋅ h )
k =1
Так как h может принять любое значение от 2 до n (все n точек множества могут лежать
на его выпуклой оболочке), то трудоемкость алгоритма Джарвиса в худшем случае является
квадратичной. Однако если h мало, то этот алгоритм является весьма эффективным.
Рис. 3. Построение выпуклой оболочки методом Джарвиса.
Достоинства:
•
Алгоритм Джарвиса может быть применен в пространствах размерности больше
двух.
•
При априорном знании малости числа вершин оболочки в теории даёт оптимальную
трудоемкость.
Недостатки:
•
Высокая квадратичная трудоемкость в худшем случае.
8
2.1.2 Алгоритм обхода Грэхема (Graham Scan)
Алгоритм Грэхема называют ([1]) первым алгоритмом вычислительной геометрии. Этот
алгоритм был описан в одной из первых работ Грэхема [5], специально посвященной вопросу разработки эффективных геометрических алгоритмов, показал, что, выполнив предварительно сортировку точек, крайние точки можно найти за линейное время. Использованный
им метод стал очень мощным средством в области вычислительной геометрии.
Алгоритм начинает свою работу с нахождения начальной точки p1 из S, которая гарантированно является вершиной выпуклой оболочки. За точку p1 берется самая левая из самых
нижних точек множества S, также, как и в методе Джарвиса. Очевидно, что точка p1 может
быть найдена за время O(n).
Далее все точки исходного множества сортируются по возрастанию полярного угла, образованного каждой текущей точкой q, при условии, что точки, находящиеся точно выше
начальной точки, обладают нулевым углом, а полярные углы растут по направлению часовой стрелки.
Рисунок 4. Порядок расположения точек в алгоритме Грэхема
Отсортированные точки следует поместить в двусвязный список (p1, p2, …, pn). Обход
Грэхема заключается в сканировании полученного отсортированного списка и удалении из
него точек, не входящих в выпуклую оболочку.
Для дальнейшего описания алгоритма введем следующее обозначение: будем говорить,
что три точки a, b и c образуют левый поворот, если точка c находится слева от прямой, образованной вектором, направленным из точки a в b.
Это делается путём «метода трех монет». Его суть такова: на каждом шаге проверяется
взаимное расположение трех точек (которые «помечены монетами»). Изначально помечаются первые три точки в отсортированном списке. Проверка состоит в определении, образуют
ли три проверяемые точки левый или правый поворот. Если точки образуют левый поворот,
то средняя из них удаляется из списка, и «монеты» двигаются назад, то есть после удаления
некоторой точки pt из тройки pt-1, pt, pt+1, точка pt+1 (вследствие удаления) становится на место pt, а помеченными становятся точки pt-2, pt-1, pt и проверка повторяется. Процесс останавливается, когда первой проверяемой точкой опять становится первая точка множества p1.
Конец алгоритма. ■
Так как за каждый просмотр мы или удаляем одну точку, или переходим к следующей, а
просмотр заканчиваем при достижении начальной точки, которая не удалится, то мы выполняем не более n шагов.
Итого общая трудоёмкость алгоритма Грэхема составляет сумму трудоемкости алгоритма сортировки и трудоемкости сканирования
9
О(n log n) + О(n) = О(n log n).
Недостатки:
•
Теоретически алгоритм Грэхема является оптимальным в худшем случае, однако он
не оптимален в среднем.
•
Алгоритм не является открытым, для его работы необходимо априорное знание всего набора точек.
•
Неизвестны обобщения алгоритма на пространства размерности больше двух.
Достоинства:
•
Алгоритм Грэхема имеет гарантированную линейно-логарифмическую трудоемкость.
2.1.3 Алгоритм монотонных цепочек Эндрю (Monotone Chain)
Алгоритм Эндрю, описанный в 1979 в [6], является модификацией алгоритма Грэхема,
которая использует лексикографическое упорядочение точек по координатам. Это является
большим преимуществом, так как в этом случае не приходится использовать вещественные
числа и тригонометрические операции. Алгоритм Эндрю по отдельности вычисляет верхнюю и нижнюю оболочки из последовательных цепей точек.
Пусть a и b – самая нижняя из самых левых и самая верхняя из самых правых точек исходного множества, соответственно. Очевидно, что a и b являются лексикографически самой
большой и самой маленькой точками множества S. Заметим, что a и b также являются вершинами выпуклой оболочки.
Пусьт (p1, p2, …, ph) – вершины выпуклой оболочки множества S, выстроенные таким образом, что p1=a. Пусть r – индекс, такой, что p1=b. Линия, соединяющая a и b, разделяет выпуклую оболочку на две полигональных цепочки (p1, p2, …, pr) и (pr, pr+1, …, ph, p1). Эти цепочки называются верхней и нижней оболочками (см. Рис 7.).
Рисунок 5. Линия, проходящая через a=p1 и b=p4 делит выпуклую
оболочку на верхнюю и нижнюю оболочки.
После такого разбиения для построения выпуклой оболочки S достаточно построить
верхнюю и нижнюю оболочки, и после объединить их. Далее будет показано, как строится
верхняя оболочка. Нижняя оболочка строится симметричным образом.
10
Для построения верхней оболочки используется подмножество точек из S, которые находятся выше линии, соединяющая a и b. Для простоты, также назовем это подмножество S,
а его размер будем обозначать n. Если n=2, то верхняя оболочка состоит из одного ребра
(a, b), так что будем считать, что n>2.
Для построения верхней оболочки точки qi множества S упорядочивается в соответствии
с возрастанием абсциссы и к полученному списку применяется метод обхода Грэхема. Для
этого алгоритм Эндрю использует стек x0, x1,…, xt для хранения текущей верхней оболочки.
Точка xt считается находящейся на вершине стека. После окончания работы алгоритма стек
содержит верхнюю оболочку множества S.
Более точное описание алгоритма таково: инвариантом при любом s является тот факт,
что
точки x0, x1,…, xt из стека образуют такую подпоследовательность множества
qn, q1, q2,…,qs, что:
1) t ≥ 2, s ≥ 2, x0 = q n = b, x1 = q1 = a, xt = q s ,
2) x1, x2,…, xt является верхней оболочкой q1, q2,…,qs,
3) точки x1, x2,…, xt отсортированы слева направо.
В стадии инициализации в стек последовательно помещаются точки q n , q1 , q 2 . Далее, последовательно выбирая по одной точке из множества {qs+1, qs+2,…,qn-1}, где s – это индекс последней проверенной точки (изначально s=2). На каждом этапе проверяется взаимное расположение точек qs+1, xt, xt-1. Пока эти точки не образуют левый поворот, верхняя точка стека
удаляется. Как только точки qs+1, xt, xt-1 стали образовывать левый поворот, точка qs+1 помещается в стек и алгоритм переходит к рассмотрению следующей точки. Легко показать, что
инвариант выполняется на всем протяжении выполнения алгоритма. Конец алгоритма. ■
Рисунок 6. Иллюстрация построения верхней оболочки в методе Эндрю
В сущности, алгоритм Эндрю является частным случаем алгоритма Грэхема, когда центральная точка выбирается бесконечно удаленной в отрицательном направлении по оси ординат, так что в этом случае упорядоченность по абсциссе совпадает с упорядоченностью по
полярному углу.
Как и алгоритм Грэхема, этот алгоритм имеет трудоёмкость О(n log n). Трудоемкость
сортировки множества S при построении каждой из оболочек (верхней и нижней) составляет
О(n log n). Процедура построения оболочки занимает время О(n), т.к. очевидно, что каждая
точка помещается и извлекается из стека не более одного раза.
11
Достоинства:
•
Алгоритм Эндрю имеет гарантированную линейно-логарифмическую трудоемкость в
худшем случае.
•
Алгоритм является более простым в реализации, чем алгоритм Грэхема.
Недостатки:
•
Алгоритм не является открытым.
•
Алгоритм не имеет обобщения на пространства размерности больше двух.
2.1.4 Алгоритм типа «Разделяй и властвуй» (Divide and conquer)
Алгоритм построения выпуклой оболочки, основанный на методе «Разделяй и властвуй»
описан в [7] Ф. Препаратой.
В данном алгоритме множество S разбивается на два примерно равномощных подмножества S’ и S’’, выпуклые оболочки которых не пересекаются Разбиение множества S происходит таким образом: сначала определяется размах множества точек по ординатам и абсциссам. Деление происходит по координате, размах по которой больше. Назовем эту координату
экстремальной. Затем за время O(n) строится медиана исходного множества S. Пусть pm –
медиана множества S. Далее множество S разбивается на две части: в одной содержатся точки, у которых значение экстремальной координаты больше, чем значение этой координаты у
точки pm, в другой половине содержатся точки, у которых значение экстремальной координаты меньше, чем значение этой координаты у точки pm, и сама точка pm. После деления алгоритм запускается рекурсивно для каждой из половин. В случае, когда количество точек в
подмножествах невелико, используется любой более простой способ построения выпуклой
оболочки.
Быстродействие метода в целом немало зависит от эффективности нахождения слияния
двух выпуклых оболочек. Пусть у нас есть выпуклые непересекающиеся многоугольники P’
и P’’, заданные списками своих вершин, отсортированных в порядке против часовой стрелки. Нам требуется найти P – их слияние, которое и будет являться выпуклой оболочкой исходного множества. Для этого находятся крайние точки каждого многоугольника a и b (самая правая для левого, самая левая для правого соответственно). После этого путем последовательных проверок выпуклости строятся верхняя и нижняя касательные к многоугольникам. Это занимает не больше n проверок. Алгоритм построения нижней касательной таков:
1) Пока a и b не являются нижней гранью, повторяем шаги a-b:
a. Пока точки p’a+1, p’a, p’’b не образуют левого поворота, передвигаем a по P’ по часовой стрелке.
b. Пока точки p’a, p’’b, p’’b+1, не образуют левого поворота, передвигаем b по
P’’против часовой стрелки.
2) Возвращаемся на шаг 1.
Как только будут выполняться условия левого поворота и для точек 2-го условия, и для
точек 3-го условия, поиск нижней касательной закончен. Конец алгоритма. ■
Очевидно, что трудоемкость такого поиска линейна относительно суммы количеств вершин в объединяемых оболочках.
12
Рис. 7. Построение нижней касательной
Общую трудоемкость метода «разделяй и властвуй» можно выразить как
if n = 1
c
T ( n) ≤
cn + 2T (n / 2) if n > 1
Развернув эту рекуррентную последовательность, получим
T ( n)
≤ cn + 2T (n / 2)
≤ cn + 2(cn / 2 + 2T (n / 4))
= 2cn + 2 2 T (n / 2 2 )
...
≤ icn + 2 i T (n / 2 i )
где i – глубина рекурсии. Очевидно, что максимальная глубина равна log n. Таким образом,
T (n) ≤ cn log n + nT (1) = O(n log n)
Достоинства:
•
Гарантированная логарифмическая трудоемкость.
•
Алгоритм можно распараллеливать.
•
Алгоритм обобщаем на произвольную размерность.
Недостатки:
•
Алгоритм относительно сложен в реализации по сравнению с другими.
2.1.5 Алгоритм «быстрого построения» (QuickHull)
Для построения выпуклой оболочки были созданы алгоритмы, напоминающие быструю
сортировку. Такие алгоритмы называются быстрыми методами построения оболочки. Одними из первых такой алгоритм предложили Эдди в [8] и Бикат в [9].
13
Рис. 8. Пример работы алгоритма быстрого построения выпуклой оболочки.
Суть алгоритма состоит в том, что исходное множество S из n точек разбивается на два
подмножества, каждое из которых будет содержать одну из двух ломаных, которые при соединении образуют выпуклую оболочку. Для начала нужно определить две точки, которые
будут являться соседними вершинами выпуклой оболочки. Можно взять самую левую (a) и
самую правую (b) вершины. После чего нужно найти точку c максимально удаленную от
прямой ab.
Алгоритм выбора с основывается на том факте, что эта точка определяет треугольник,
попадая в который, будут отбрасываться точки. Для того, чтобы максимизировать число точек, подлежащих удалению, разумным было бы найти точку c такой, чтобы она максимизировала площадь треугольника abc. Одновременно с тем, точка c должна лежать по левую
сторону от отрезка ab. Таким образом совместив эти два условия, определяем, что за точка c
выбирается та точка из S \ {a,b}, которая максимизирует значение ∆(a, b, c) .
Все точки, лежащие в треугольнике abc исключаются из дальнейшего рассмотрения. Для
того, чтобы на каждом шаге исключать как можно больше точек, точка c выбирается по критерию наибольшей площади треугольника abc. Остальные точки будут делиться на два подмножества: точки, которые лежать левее ac и точки, которые лежат правее и cb. Каждое из
них содержит ломаные которые в сочетании с a, b и c дают выпуклую оболочку. С каждым
из них проделываем то же самое. В подмножестве точек , лежащих левее cb выбираем c’ по
тем же признакам, по которым выбирали точку c, максимально удаленную от cb, которая делит его на три части. Из них одна выбрасывается, а остальные делятся опять. Это реализуется рекурсивной процедурой, которая для данного ей множества возвращает соответствующую часть выпуклой оболочки. Конец алгоритма. ■
В случае, когда мощность каждого, из подмножеств, на которое делится множество, не
превосходит некоторой константы умноженной на мощность множества, получаем сложность алгоритма, как и в быстрой сортировке O(n log n). Но в худшем случае может потребоваться время O(n2).
Достоинства:
•
Алгоритм можно распараллеливать.
•
Алгоритм обобщаем на произвольную размерность.
Недостатки:
• Высокая квадратичная трудоемкость в худшем случае.
2.1.6 Алгоритм Чена
До сих пор было рассмотрено два типа алгоритмов построения выпуклой оболочки:
14
Алгоритм Грэхема, его модификации, алгоритм «разделяй и властвуй», быстрый ал1.
горитм построения выпуклой оболочки. Эти алгоритмы имеют трудоемкость O(n log n)
2.
Обход Джарвиса. Если за h обозначить количество вершин выпуклой оболочки, то
этот алгоритм имеет трудоемкость O(nh). Такие алгоритмы, трудоемкость которых зависит и
от n (размера входных данных), и от h (размера выходных данных), называются чувствительными к результату.
Стоит заметить две вещи. Во-первых, алгоритмы первого типа оптимальны в среднем.
Однако, если предположить, что h, – количество вершин выпуклой оболочки, мало, то трудоемкость алгоритма Джарвиса меньше, чем у алгоритмов первого типа. К примеру, если h
известно заранее или постоянно, то алгоритм Джарвиса имеет линейную трудоемкость, тогда
как алгоритмы из первой группы всё равно имеют логарифмическую трудоемкость. С другой
стороны, если h гораздо больше, чем log n, то алгоритм Джарвиса проигрывает. К примеру,
если h=n, то этот алгоритм показывает квадратичную трудоемкость.
Эти рассуждения наводят на следующую проблему: существует ли алгоритм, по крайней
мере такой же быстрый, как оба вышеприведенных класса алгоритмов на любых входных
данных.
Оказывается, существуют даже более быстрые алгоритмы. Это было показано в 1986 году в [10] Киркпатриком и Зейделем. Они описали весьма алгоритм с трудоемкостью
O(n log h). Однако этот алгоритм имел чрезвычайно сложную логику.
Позже, в 1994 году, в [3, 15, 16] Тимоти Чен предложил чрезвычайно простой алгоритм с
трудоемкостью O(n log h). Алгоритм Чена является оригинальным обобщение алгоритмов
Джарвиса и Грэхема.
Предположим, что нам известно количество вершин выпуклой оболочки h. Тогда алгоритм Чена можно описать следующим образом:
Шаг 1. Произвольно разделим исходное множество S на подмножества S , S , ..., S ,
1 2
n/h
каждое (кроме, возможно, последнего) размером h.
Шаг 2. Для каждого i, 1 ≤ i ≤ n / h , найдем выпуклую оболочку множества точек Si и
обозначим её Ci.
Шаг 3. Теперь переходим к вычислению выпуклой оболочки всего множества S, используя методику «заворачивания подарка». Алгоритм начинает свою работу с нахождения точки p0 из S, которая гарантированно является вершиной выпуклой оболочки S. Обычно за точку p0 берется самая нижняя из точек множества S. Если S содержит несколько точек с минимальной ординатой, то берется самая левая из них. Очевидно, что точка p0 может быть найдена за время O(n). Пусть p1 – точка множества S, такая, что ребро p0 p1 является ребром
выпуклой оболочки, направленным против часовой стрелки. Далее рассмотрим, каким образом следует находить p1.
Пусть l – луч, направленный из p0 в сторону положительного направления оси абсцисс.
Заметим, что все точки множества S находятся левее этого луча или на нем. Для каждого i,
1 ≤ i ≤ n / h мы находим точку q i ∈ S i , которая является первой точкой, которой коснется
луч l, если его вращать против часовой стрелки. Далее, за линейное время мы можем найти
точку qj из множества {q , q , ..., q } , для которой угол между l и p0qj минимален (если
1 2
n/h
таких точек несколько, то выбирается из них та, расстояние от которой до точки p0 максимально). Очевидно, что точка qj и является искомой точкой p1.
15
Рисунок 9. Алгоритм Чена
Найдя p1, мы таким же образом находим точку p2: пусть l' – луч, направленный из p0 и
проходящий через p1. Как и ранее, все точки множества S находятся левее луча или на нем.
Для каждого i, 1 ≤ i ≤ n / h мы выполняем «запрос на экстремальность», то есть находим
точку q i ∈ S i , которая является первой точкой, которой коснется луч l', если его вращать
против часовой стрелки относительно точки p0. Тогда p2 – это та точка x из n / h точек qi ,
для которой угол между l' и p1x минимален. Мы продолжаем выполнять такие шаги «заворачивания подарка», пока не вернемся к исходной точке p0. Конец алгоритма. ■
Подсчитаем трудоемкость вышеприведенного алгоритма. Шаг 1 занимает время O(n).
Выпуклая оболочка для каждого из исходных подмножеств Si может быть найдена за время
O( S i log S i ) = O(h log h) .
Таким образом, Шаг 2 в целом имеет трудоемкость
n
O( log h) = O(n log h) .
h
Рассмотрим Шаг 3. Начальная точка p0 может быть найдена за линейное время. Для нахождения p1 мы выпоняем «запрос на экстремальность» в каждом из подмножеств Si. Если
осуществлять эти запросы с использованием метода бинарного поиска, описанного ниже в
п.2.2.2, то каждый такой запрос будет иметь трудоемкость
O(log S i ) = O(log h) .
Таким образом, все запросы вместе займут время
n
O( log h) .
h
16
Это даст нам n / h точек-кандидатов на попадание в выпуклую оболочку. За время
O(n / h) мы выбираем из них точку p1. Следовательно, имея p0, мы находим p1 алгоритмом с
трудоемкостью O(n / h log h) .
Так как в выпуклой оболочке h вершин, то общая трудоемкость их нахождения такова:
n
O(n + h * log h) = O(n log h)
h
То есть, весь алгоритм нахождения выпуклой оболочки множества S имеет трудоемкость
O(n log h).
Однако заметим, что это выполняется только при условии априорной известности h. Как
должен поступать алгоритм, если h не известно? Трюк состоит в том, что мы «подберем» необходимое значение h следующим специальным способом.
Предположим, что H – это текущее предполагаемое значение h. Мы запускаем вышеприведенный алгоритм, заменив h на H. Шаги 1 и 2 выполняются за время O(n log H). На шаге 3
может получиться две различных ситуации:
1. За H шагов заворачивания подарка мы вернулись в точку p0. Это может произойти,
только если h ≤ H . В этом случае, выпуклая оболочка S с учетом трудоемкости третьего шага алгоритма может быть построена за время
O(n + h
n
log H ) = O(n log H )
H
2. После H шагов заворачивания подарка мы не достигли точки p0. Это может произойти, только если h > H, то есть наше предположение о количестве вершин выпуклой оболочки
было слишком мало. В этом случае мы останавливаем алгоритм после H шагов. При этом мы
затратили время O(n logH), но так и не нашли выпуклой оболочки множества S. Так как наше
предположение о величине h было слишком мало, мы увеличиваем H и запускаем алгоритм
снова.
Какие значения необходимо давать H на первом и последующих шагах приближения?
Обычно начинают с H=4 или любого другого небольшого числа. Каждый раз, когда обнаруживается, что h<H, будем принимать H=H2
Пусть Hf – финальное значение H. То есть, запуская алгоритм в предположении, что количество вершин выпуклой оболочки равно Hf, мы успешно заканчиваем построение выпуклой оболочки не более чем за Hf шагов. Тогда мы знаем, что Hf ≥ h. Предыдущее предполагаемое значение, которое было равно H f , оказалось слишком мало, то есть Hf < h2.
Теперь мы можем вычислить трудоемкость алгоритма в целом. Для каждого предполагаемого значения H мы тратим времени не больше c n log H. Следовательно, на финальном
шаге мы тратим времени не больше c n log Hf. Трудоемкость предпоследнего шага не больше
c ⋅ n log H f =
1
c ⋅ n log H f .
2
В общем, для i-го шага подбора H мы тратим времени не больше
i
1
c ⋅n log 2 i H f = c ⋅n log H f .
2
Тогда общее время работы алгоритма равно
17
i
1
c ⋅ n log H
∑
f
i ≥0 2
≤ 2c ⋅ n log H
f
≤ 2c ⋅ n log h 2
≤ 4c ⋅ n log h
= O(n log h).
Полученная трудоемкость говорит о том, что цель – найти алгоритм, имеющий преимущества методов Грэхема и Джарвиса, достигнута. В среднем этот алгоритм имеет трудоемкость O(n log h). В худшем случае этот алгоритм будет иметь трудоемкость O(n log n).
Достоинства:
• Алгоритм имеет трудоемкость O(n log h) в среднем, при этом в худщем случае он является оптимальным.
Недостатки:
•
Алгоритм не является открытым, т.е. необходимо априорное знание всего множества
точек.
2.2 Особенности практической реализации алгоритмов построения выпуклой оболочки на плоскости
Все описания алгоритмов, приведенные выше, являются чисто теоретическими. При
практической реализации конкретных алгоритмов возникает множество проблем, которые в
теории не решаются и чаще всего даже и не возникают. Решение этих задач иногда позволяет существенно увеличить реальную скорость работы программы, реализующей тот или
иной алгоритм.
2.2.1 Практические особенности сравнения углов
В большинстве алгоритмов построения выпуклой оболочки необходимо искать минимальные углы среди множества углов, заданных парами векторов. Однако очевидно, что выполнение тригононометрических операций существенно снижает скорость работы алгоритма. Ниже приведено описание известного способа избавления от тригонометрических операций [1].
Пусть a и b – две последовательные (против часовой стрелки) вершины выпуклой оболочки, а l – линия, проходящая через эти вершины. Будем считать, что эта линия является
вектором, имеющим направление из a в b. Заметим, что все точки множества S находятся
или левее l или на l.
Для каждой точки q ∈ S \ {b} пусть αq – угол между l и отрезком bq. Алгоритм Джарвиса ищет такую точку q, для которой этот угол является минимальным. Мы можем явно найти
все углы αq, а потом найти минимальный из них. Рассмотрим способ нахождения этих углов.
Во-первых, заметим, что αq – это угол между векторами b-a и q-b (см. рис. 4).
18
Рис. 10. Вычисление угла αq
Также заметим, что
(b − a ) ⋅ (q − b ) =
b − a × q − b × cos α q .
Следовательно,
.
2
2
(q x − bx ) + (q y − b y )
(bx − a x )(q x − bx ) + (b y − a y )(q y − b y )
α q = arccos
(bx − a x ) 2 + (b y − a y ) 2
Но сравнение этих углов в явном виде влечет большие вычислительные затраты. Опишем
способ нахождения минимального угла αq без использования функций арккосинуса и вычисления квадратного корня. Для того, чтобы найти минимальный угол, не обязательно вычислять углы, достаточно их сравнивать. То есть, имея две точки q и r, нам достаточно определить, α q < α r , α q > α r , или α q = α r . Это можно сделать, не вычисляя точных значений углов. Рассмотрим следующий определитель:
bx
∆(b, q, r ) = q x
rx
by 1
(q x − bx ) (q y − b y )
qy 1 =
(rx − bx ) (ry − b y )
ry 1
(1)
Из аналитической геометрии мы знаем, что его значение равно удвоенной ориентированной площади треугольника bqr, знак которого положителен, если α q < α r , отрицателен, если
α q > α r , и равен нулю, если α q = α r (рис. 10). Таким образом, мы можем сравнивать углы,
вычисляя знак выражения
∆(b, q, r ) = (q x − bx )(ry − b y ) − (q y − b y )(rx − bx ) .
(2)
Это займет всего пять вычитаний и два умножения, что намного проще, чем вычисление
арккосинусов и квадратных корней.
Если существует более одной точки, имеющей минимальный угол α, необходимо выбрать ту из них, расстояние от которой до точки b максимально. Конечно, мы для каждой
такой точки q с минимальным углом α мы можем вычислить расстояние
d (b, q) = (bx − q x ) 2 + (b y − q y ) 2 ,
19
(3)
а потом выбрать ту точку, для которой
Рис. 11. ∆ - удвоенная ориентированная площадь треугольника bqr
d (b, q) минимально. На самом деле вычислять расстояние не обязательно – достаточно
всего лишь сравнить расстояния d (b, q) и d (b, r ) . Для того, чтобы не вычислять квадратных
корней, можно использовать следующее соотношение:
d (b, q ) < d (b, r ) ⇔ (bx − q x ) 2 + (b y − q y ) 2 < (bx − rx ) 2 + (b y − ry ) 2 .
Для ускорения практической работы алгоритма это делается с использованием формул
(1) и (2). Если углы совпадают, то точки сортируются относительно расстояния от центра
координат (с использованием формулы (3)).
Во многих алгоритмах используется следующая примитивная операция: пусть x, y и z –
три несовпадающие точки. Тогда считается, что (x, y, z) является правым поворотом, если
точка z находится справа от отрезка, направленного из x в y. Если z находится слева от отрезка, направленного из x в y, то (x, y, z) является левым поворотом.
Из формул (1) и (2) следует, что
если ∆( x, y, z ) < 0;
если ∆( x, y, z ) > 0.
правым поворотом,
( x, y, z ) является
левым поворотом,
(4)
Если ∆( x, y, z ) = 0 , то точки x, y, z считаются коллинеарными.
2.2.2 Иерархическое представление выпуклых оболочек. Практические особенности реализации алгоритма Чена.
В алгоритме Чена предполагается, что выполнение «запроса на экстремальность» имеет
логарифмическую трудоемкость. Эта трудоемкость может быть достигнута, только с использованием специализированной структуры данных. Структура, удовлетворяющая вышеописанным требованиям, была описана Чазелем и Добкиным в [11].
Рассмотрим следующую проблему: имеется множество S, состоящее из n точек. Необходимо хранить это множество в такой структуре данных, которая позволяет отвечать на «запросы на экстремальность».
Смысл такого запроса заключается в следующем. Пусть дана некая точка q на плоскости
и луч l, направленный из q вправо. Все точки множества S лежат или на луче l или слева от
него. Ответом на запрос будет являться точка, которую l коснется первой, если его вращать
вокруг точки q против часовой стрелки (рис. 12).
20
Рис. 12. Если вращать l вокруг q, то первой точкой, которую коснется l, будет точка p
Очевидно, что точка p может быть ответом на запрос на экстремальность только если она
является вершиной выпуклой оболочки множества S. Следовательно, в искомой структуре
данных необходимо хранить только точки выпуклой оболочки. Пусть P = ( p 0 , p1 , ... , p h −1 ) –
вершины выпуклой оболочки S, пронумерованные в порядке против часовой стрелки. Будем
хранить эти точки, используя иерархическое представление P. Это представление выглядит
следующим образом: пусть P0=P. Для каждого i > 0 определим Pi как последовательность,
полученную из Pi-1 удалением каждой второй точки, начиная с точки, имеющей нулевой индекс. Пусть k – такой индекс, что Pk содержит ровно два элемента. Тогда список последовательностей H ( P ) = ( Po , P1 , ... , Pk ) называется иерархическим представлением последовательности P (рис. 13). Очевидно, что k < log h.
Рисунок 13. Иерархическое представление выпуклого многоугольника P состоит из
P0=P, P1=(p0, p2, p4, p6, p8, p10), P2=(p0, p4, p8), P3=(p0, p8)
Процедура построения иерархического представления такова:
1. Вычислим выпуклую оболочку S, используя, к примеру, обход Грэхема. Это даст нам
последовательность P0.
2. Для каждого i =1,2,… построим последовательность Pi на основе Pi-1, удаляя каждую
вторую точку.
21
Первый шаг этого алгоритма имеет трудоемкость O(n log n). Трудоемкость второго шага
k
равна O(∑i =0 hi ) = O(n) . Таким образом, иерархическое представление какого-либо множества может быть получено за время O(n log n).
Однако даже вышеприведенный алгоритм не годится для применения на практике из-за
большого количества используемой памяти. Автором было предложено хранить только число k – количество уровней в иерархическом представлении, а для выполнения экстремальных запросов использовать следующий алгоритм, имитирующий прохождение по слоям иерархического представления:
Зная k, сравнить углы для точек p и p . Используя формулу (4), выбрать
0
2k
точку p, сохранить её индекс r.
Шаг 1.
Шаг 2. Для каждого е = k − 1, k − 2, ...,0 , повторяем следующие действия: сравниваем
углы у точек p=pr, p
и p
, ту из них, которая имеет наименьший угол по отношеr + 2e
r − 2e
нию к l, сохраняем в p, а её индекс – в r.
После окончания этого алгоритма в p будет лежать точка, являющаяся ответом на экстремальный запрос к исходному множеству точек.
2.3 Алгоритмы построения выпуклых оболочек в трехмерном пространстве
2.3.1 Алгоритм «грубой силы»
Этот алгоритм является простейшим алгоритмом для построения выпуклой оболочки
множества S, состоящего из n точек в трехмерном пространстве.
Смысл алгоритма заключается в проверке каждой тройки точек на образование потенциальной грани выпуклой оболочки путем перебора всех остальных точек и проверки их взаимного расположения.
Проверка осуществляется следующим образом: для каждой тройки точек pi,pj,pk мы перебираем точки q ∈ S \ {pi , p j , p k }. Если все точки q находятся по одну сторону от треугольни-
ка abc, то этот треугольник является гранью выпуклой оболочки.
В целях ограничения перебора нам необходимо выбирать точки pi,pj,pk таким образом,
чтобы проверять каждую тройку только один раз. Это можно сделать, наложив на точки
pi,pj,pk следующие условия: индексы j и k, и проекция пространственного треугольника
pi,pj,pk на плоскость xOy должна образовывать левый поворот. Конец алгоритма. ■
Трудоемкость этого алгоритма составляет O(n4).
2.3.2 Алгоритм «заворачивания подарка»
Алгоритм, использующий метод «заворачивания подарка», строит выпуклую оболочку
множества S, состоящего из n точек в трехмерном пространстве за время O(nh), где h – это
количество граней выпуклой оболочки.
Основная идея этого метода состоит в последовательной генерации граней выпуклой
оболочки путем поиска в ширину или в глубину.
Алгоритм состоит из двух стадий: инициализации и серии шагов «заворачивания».
22
Инициализация. Сначала необходимо найти точку p с минимальной z-координатой (Если таких точек несколько, то берется та из них, которая имеет наименьшую абсциссу, а если
и таких точек несколько, то та, которая имеет наименьшую ординату). Пусть H – плоскость,
проходящая через p и перпендикулярная к оси z, и l – линия на плоскости H, на которой лежит точка p. Далее мы находим точку q, которая образует минимальный угол между H и
плоскостью G, которая содержит q и линию l. Пусть m – линия, проходящая через p и q. Заметим, что m принадлежит плоскости G. Завершается стадия инициализации нахождением
точки r, которая образует минимальный угол между G и плоскостью F, которая содержит r и
линию m. Плоскость F содержит грань выпуклой оболочки множества S, которая образована
треугольником T = ∆pqr . Определим стек Q текущих ребер и поместим в него все ребра
треугольника T.
Шаг алгоритма. На каждом шаге «заворачивания» мы извлекаем из стека Q одно из ребер e. Это ребро инцидентно какой-то грани T выпуклой оболочки S. Мы находим треугольник U, отличный от T, такой, что он является гранью выпуклой оболочки. Это делается путем нахождения точки s, которая образует минимальный угол между плоскостью F, содержащей T, и плоскостью E, которая содержит s и e. Если треугольник U, определяемый точкой s и ребром e, ещё не был обнаружен ранее, то мы добавляем два его ребра, отличные от
e в стек Q и, естественно, запоминаем треугольник U.
Этот шаг повторяется до тех пор, пока стек Q не станет пустым. Когда это выполнится, в
списке сохраненных треугольников мы будем иметь выпуклую оболочку множества S. Конец
алгоритма. ■
Так как на каждом шаге мы находим одну точку из исходного множества S, то трудоемкость шага этого алгоритма равна O(n). Учитывая, что h – это количество граней выпуклой
оболочки, мы сделаем не более h шагов. Таким образом, трудоемкость алгоритма «заворачивания подарка» равна O(nh). Как и в плоском случае, алгоритм, основанный на этой методике, будет полезен при малых h, так как в случае, когда все точки множества S входят в выпуклую оболочку, этот алгоритм будет иметь квадратичную трудоемкость.
2.3.3 Алгоритм «разделяй и властвуй»
Этот алгоритм, предложенный Препаратой и Хонгом в [12], основан на методике «разделяй и властвуй», и, в отличие от предыдущего, имеет гарантированную линейнологарифмическую трудоемкость в худшем случае.
Алгоритм начинает свою работу с разделения множества S на примерно равные по мощности подмножества S1 и S2, отделяемые друг от друга некоторой плоскостью H, которая
перпендикулярна оси, по которой координаты точек множества S имеют наибольший размах.
Далее мы рекурсивно находим выпуклые оболочки множеств S1 и S2 – C1 и C2 соответственно. Затем необходимо найти «мост» между этими двумя многогранник. Сначала мы проr
ецируем C1 и C2 на некоторую плоскость G в направлении r , параллельном H, и находим
некоторое ребро e между двумя спроецированными двумерными выпуклыми оболочками.
Проецируя точки назад в трехмерное пространство, мы можем увидеть, что ребро e переходит в ребро, (p,q) соединяющее точки p на С1 и q на С2. Более того, плоскость W, содержащая
r
это ребро и вектор r , является касательной к выпуклой оболочке множества S. Дальнейшее
вычисление моста заключается в последовательном нахождении треугольников, принадлежащих выпуклой оболочке, состоящих из ребра на одном из многогранников C1 или C2, и
точки на другом из них.
Нахождение треугольников, формирующих мост, начинается с уже найденного ребра
(p,q). Таким образом, на каждом шаге мы имеем некоторое ребро (p,q) такое, что p находится
на С1 и q находится на С2. Проверив вершины С1, инцидентные вершине p, мы можем найти
23
ребро (p,r) на С1, которое образует минимальный угол с плоскостью W. Аналогично, проверив вершины из С2, инцидентные q, мы можем найти ребро (q,s) на С2, которое образует минимальный угол с плоскостью W. Тот из треугольников pqs и prq, который образует минимальный угол с плоскостью W, будет являться следующим треугольником моста. Далее алгоритм продолжает вычисления, начиная с другого ребра полученного треугольника, вершины которого находятся на C1 и C2. Эти вычисления продолжаются до тех пор, пока алгоритм
не вернется к первому ребру. Конец алгоритма. ■
Такой алгоритм вычисления моста имеет трудоемкость O(n). Тогда общая трудоемкость
алгоритма построения выпуклой оболочки будет равна O(n log n).
2.4 Обзор областей применения
2.4.1 В ГИС и САПР
В ГИС и САПР одно из наиболее серьезных применений средств вычислительной геометрии является задача моделирования различных поверхностей, представляемых в виде
триангуляций, в частности триангуляции Делоне [13]. В настоящее время одним из перспективных направлений быстрого вычисления триангуляции Делоне является применение алгоритма построения трехмерной выпуклой оболочки по специально сформированному набору
точек в пространстве . В настоящее время разработаны различные программы построения
триангуляции Делоне на основе трехмерных выпуклых оболочек, имеющих очень приличное
время работы по сравнению с другими известными алгоритмами [14].
Другой пример применения – это диаграмм Вороного и различные виды их обобщения.
Диаграммы Вороного очень удобно строить по триангуляции Делоне, которая, в свою очередь, может быть построена с помощью трехмерных выпуклых оболочек.
2.4.2 Другие области
Также алгоритмы построения выпуклых оболочек широко используются во многих областях науки и техники.
Ниже следует перечисление некоторых областей применения алгоритмов построения выпуклых оболочек:
•
СУБД. Для выполнения запросов на экстремальность данных по нескольким параметрам.
•
Робототехника. Для определения оптимальных путей обхода препятствий
•
Материаловедение. В широко используемом методе конечных автоматов.
•
Кристаллография. Для облегчения изучения поверхностей кристаллов.
•
Компьютерные сети. Выпуклые оболочки используются в алгоритмах маршрутизации.
2.5 Существующие проблемы в области разработки алгоритмов построения выпуклых оболочек
Существует несколько проблем, ограничивающих использование стандартных теоретических алгоритмов построения выпуклой оболочки. Приведем некоторые из них:
1. Стремительный рост объёмов данных. В настоящее время в коммерческих системах, использующих алгоритмы построения выпуклой оболочки, объёмы данных настолько
велики, что существующие алгоритмы, которые имеют временную сложность O(n3/2) или
O(n log n), не справляются с задачей за приемлемое время. Вследствие этого возникает необ24
ходимость разработки алгоритмов с временной сложностью O(n) в среднем или близкой к
ней.
2. Вычислительная устойчивость. Существующие алгоритмы построения выпуклой
оболочки являются чисто теоретическими, не привязанными к конкретным данным, моделям
вычислений и платформам. Вследствие этого в практических реализациях этих алгоритмов
имеет место вычислительная неустойчивость, что неизбежно ведет к потерям в качестве работы алгоритмов.
3. Недостаточное количество работ, посвященных анализу и/или обзору алгоритмов построения выпуклой оболочки, особенно на русском языке.
25
3 Модификации алгоритмов
В данной главе описаны некоторые известные и предложенные автором модификации
существующих алгоритмов, предназначенные для ускорения скорости их быстродействия.
3.1 Модификации алгоритмов на плоскости
3.1.1 Отсечение восьмиугольником
В качестве предварительной обработки исходного множества точек для отсечения тех
точек, которые заведомо не попадут в выпуклую оболочку, было предложено провести отсечение точек, которые попадают в специально построенный восьмиугольник. Похожая методика была применена Эклом в
Алгоритм построения восьмиугольника таков: его вершинами являются точки, имеющие
наибольшую x-координату; наибольшую сумму координат; наибольшую y-координату; наименьшую разность координат x и y; наименьшую x-координату; наименьшую сумму координат; наименьшую y-координату; наибольшую разность координат x и y соответственно.
Восьмиугольник представляется в виде множества точек f0, f1,…, f8, причем точки с индексами от 0 до 7 определяются в вышеприведенном порядке, а точка f8 принимается равной точке f0.
Рисунок 14. Формирование восьмиугольника
Далее для каждой точки pi ∈ S проводится проверка попадания в восьмиугольник. Для
каждого j=0..7 если точки pi,fj,fj+1 образуют левый поворот, то точка pi выбрасывается из
дальнейшего рассмотрения алгоритмом построения выпуклой оболочки.
Однако данный метод предобработки исходного множества точек имеет свои недостатки:
восьмикратная проверка всех точек с вычислением на каждом шаге ориентированной площади треугольника может занять слишком большое время.
Трудоемкость данного метода отсечения составляет, очевидно, O(n).
26
В силу того факта, что множество точек, оставшихся после отсечения, сильно растянуто
к краям, автором рекомендуется использовать для окончательного построения выпуклой
оболочки метод Грэхема, который имеет высокое быстродействие на таких распределениях
входных данных.
Рисунок 15. В результате отсечения из двадцати точек останутся только девять.
3.1.2 Отсечение прямоугольником
Метод отсечения прямоугольником является гораздо более эффективным, чем предыдущий метод, потому что он избавлен от необходимости вычисления площадей.
Суть метода отсечения прямоугольником состоит в следующем. Сначала находятся четыре точки, на основании которых будет построен прямоугольник. Этими точками являются
точки, обладающие следующими свойствами:
• Точка p1 - имеющая наибольшую сумму координат x и y;
• Точка p2 - имеющая наименьшую разность координат x и y;
• Точка p3 - имеющая наименьшую сумму координат x и y;
• Точка p4 - имеющая наибольшую разность координат x и y.
27
Рисунок 16. Точки, на основе которых строится прямоугольник
Далее находятся четыре значения:
•
Xmin: максимум из значений x-координаты точек p2 и p3;
•
Xmax: минимум из значений x-координаты точек p1 и p4;
•
Ymin: максимум из значений x-координаты точек p3 и p4;
•
Ymax: минимум из значений x-координаты точек p2 и p1;
Эти значения и определяют прямоугольник, используемый для отсечения заведомо ненужных точек.
Рисунок 17. Отсекающий прямоугольник. Из десяти точек пять отсекаются.
Такое отсечение, хоть и менее эффективно с точки зрения покрываемой поверхности, гораздо эффективнее с точки зрения быстродействия, так как для каждой точки требуется всего лишь проверить попадание каждой из координат в заданный интервал.
Также, как и в случае использование отсечения восьмиугольником, автором рекомендуется использовать для окончательного построения выпуклой оболочки метод Грэхема, который имеет высокое быстродействие на распределениях входных данных, похожих на множество, остающееся после применения отсечения прямоугольником.
3.1.3 Модифицированный алгоритм Чена
Проанализировав алгоритм Чена, который имеет оптимальную трудоемкость O(n log h),
автор пришел к выводу, что этот алгоритм можно модифицировать, увеличив его быстродействие.
28
Несмотря на приемлемую теоретическую трудоемкость, алгоритм Чена делает слишком
много излишних действий, которые, несомненно, уменьшают его быстродействие:
•
Каждый шаг подбора значения h включает в себя построение выпуклых оболочек
частей исходного множества точек. Однако результаты этого построения учитываются однобоко – только для построения текущего участка выпуклой оболочки. При этом
в алгоритме не предусмотрено какого-либо влияния результатов одного шага на другой.
С точки зрения автора, весьма целесообразным было бы использовать результаты построения выпуклых оболочек частей исходного множества для отсечения точек,
которые заведомо не попадут в выпуклую оболочку множества в целом. Очевидно,
что точки, отброшенные во время построения выпуклой оболочки какой-либо части
исходного множества, должны быть отброшены и из точек – потенциальных вершин
выпуклой оболочки всего множества. Рассмотрим рис. 18. Мы можем отбросить точки p1, p4, p8, p10, p11, p12, p18.
Рисунок 18. Отсечения в алгоритме Чена
Использование этого отсечения позволит улучшить скорость работы алгоритма Чена.
•
После построения части выпуклой оболочки, если H оказалось меньше реального h,
то алгоритм Чена увеличивает H и начинает построение оболочки снова.
Если же сохранять часть оболочки, полученную на предыдущих шагах, то
можно увеличить скорость работы алгоритма.
Алгоритм Чена, использующий приведенные улучшения: первоначальное отсечение точек прямоугольником, отсечение точек на каждом шаге работы алгоритма, а также сохранение уже построенных граней выпуклой оболочки, автором был назван модифицированным
алгоритмом Чена.
29
3.2 Модификация алгоритмов в пространстве
Аналогично приведенному в параграфе 3.1.2 методу предобработки исходного множества точек отсечением прямоугольником, можно привести алгоритм отсечения параллелепипедом для алгоритмов построения выпуклой оболочки в трехмерном пространстве.
Суть метода отсечения параллелепипедом состоит в следующем. Сначала находятся восемь точек, на основании которых будет построен параллелепипед. Этими точками являются
точки, обладающие следующими свойствами:
•
Точка p1 - имеющая наибольшее значение выражения (x + y + z);
•
Точка p2 - имеющая наибольшее значение выражения (x + y - z);
•
Точка p3 - имеющая наибольшее значение выражения (x - y + z);
•
Точка p4 - имеющая наибольшее значение выражения (x - y - z);
•
Точка p5 - имеющая наибольшее значение выражения (-x + y + z);
•
Точка p6 - имеющая наибольшее значение выражения (-x + y - z);
•
Точка p7 - имеющая наибольшее значение выражения (-x - y + z);
•
Точка p8 - имеющая наибольшее значение выражения (-x - y - z).
Далее находятся шесть значений:
•
Xmin: максимум из значений x-координаты точек p5, p6, p7, p8;
•
Xmax: минимум из значений x-координаты точек p1, p1, p3, p4;
•
Ymin: максимум из значений y-координаты точек p3, p4, p7, p8;
•
Ymax: минимум из значений y-координаты точек p1, p2, p5, p6;
•
Zmin: максимум из значений z-координаты точек p2, p4, p6, p8;
•
Zmax: минимум из значений z-координаты точек p1, p3, p5, p7;
Эти значения и определяют параллелепипед, используемый для отсечения заведомо ненужных точек.
30
4 Исследование алгоритмов на плоскости
4.1 Методика исследования
Для количественного анализа описанных алгоритмов построения выпуклых оболочек на
плоскости автором было проведено моделирование работы различных алгоритмов построения выпуклых оболочек на различных распределениях точек. При этом анализировалась
скорость работы алгоритмов.
Для сравнения алгоритмов в различных условиях в экспериментах строились наборы
2
данных, располагавшимися в единичном квадрате [ 0,1 ) , со следующими характеристиками:
1. Равномерное распределение. Всех точки были распределены равномерно и независимо в единичном интервале.
2. Нормальное распределение. Все точки размещались в единичном квадрате по нормальному распределению с центром в точке (0,5; 0,5) и среднеквадратическим отклонением 0,1. Точки, попадавшие за пределы единичного квадрата, отбрасывалась.
3. Распределение Лапласа. Все точки размещались в единичном квадрате по распределению Лапласа с центром в точке (0,5; 0,5). Точки, попадавшие за пределы единичного квадрата, отбрасывалась.
4. Распределение точек на окружности. Все точки были равномерно распределены по
окружности радиуса 0.5 с центром в точке (0,5; 0,5).
5. Кластерное распределение. Внутри единичного квадрата случайно выбиралось (равномерно и независимо по обеим координатам) случайное количество точек, которые
становились центрами кластеров. Внутри кластеров точки распределялись по равномерному распределению в окружности случайного радиуса, описанной вокруг центра
кластера.
В параграфах 3.2.1 – 3.2.5 приведены результаты моделирования работы различных алгоритмов построения выпуклой оболочки на различных типах экспериментальных данных.
[17] Эксперименты проводились на машине с процессором Athlon 750, среднее время построения выпуклой оболочки представлено в миллисекундах. Во всех таблицах данные верны с относительной точностью 1% при доверительной вероятности 0,95.
31
4.2 Результаты исследования
4.2.1 Равномерное распределение точек
Рисунок 19. Пример равномерного распределения исходного множества точек
Рисунок 20. График времени работы алгоритмов на равномерном распределении
32
4.2.2 Нормальное распределение точек
Рисунок 21. Пример нормального распределения исходного множества точек
Рисунок 22. График времени работы алгоритмов на нормальном распределении исходного множества точек
33
4.2.3 Лапласовское распределение точек
Рисунок 23. Пример лапласовского распределения исходного множества точек
Рисунок 24. График времени работы алгоритмов на лапласовском распределении исходного множества точек
34
4.2.4 Распределение точек на окружности
Рисунок 25. Пример распределения исходного множества точек на окружности
В силу того, что алгоритмы Джарвиса и Чена (включая модифицированный) на данном
распределении, согласно теории имели худшую трудоемкость, а на практике уже на 5000 точек завершали вычисления только по истечении двух минут для каждого теста, то автором
было принято решение не проводить эксперименты с использованием данного алгоритма.
Аналогичные проблемы проявляются и при проведении экспериментов с методом «Разделяй и властвуй», который показывает слишком высокое время работы. Поэтому этот алгоритм также был исключен из экспериментов.
Рисунок 26. График времени работы алгоритмов распределении исходного множества точек на окружности
35
4.2.5 Кластерное распределение точек
Рисунок 27. Пример кластерного распределения исходного множества точек
По тем же причинам, что и в пункте 4.2.4, из рассмотрения были исключены алгоритмы
Джарвиса и «Разделяй и властвуй».
Рисунок 28. График времени работы алгоритмов на кластерном распределении исходного множества точек
36
4.3 Анализ результатов
Результаты проведенных экспериментов показали, что различные алгоритмы ведут себя
на различных классах входных данных. Практически на всех распределениях лучшую скорость работы показал модифицированный алгоритм Чена, использующий предобработку
прямоугольником, в основном работающий чуть быстрее алгоритма Грэхема, использующего тот же метод предобработки. Однако, несмотря на использование множества улучшений,
модифицированный алгоритм Чена остался чувствительным к результату, что показали результаты его тестирования. При распределении точек на окружности этот алгоритм уже на
пяти тысячах точек работал в среднем в течение двух секунд, что было примерно в 200 раз
больше, чем у других алгоритмов.
4.4 Комбинированный алгоритм
На основе результатов экспериментов автором был предложен «комбинированный алгоритм» построения выпуклой оболочки, использующий преимущества алгоритмов на наиболее благоприятных для них распределениях данных. Комбинированный алгоритм основан на
модификации алгоритма Чена, предложенной автором. Так как эксперименты показали чрезвычайно высокое время работы как обычного, так и модифицированного алгоритмов Чена на
распределениях данных, в которых число вершин выпуклой оболочки велико и близко к общему количеству точек, то на таких распределениях комбинированный алгоритм использует
метод Грэхема для построения выпуклой оболочки.
После описания комбинированного алгоритма были проведены повторные эксперименты, в которых учавствовали только следующие алгоритмы:
•
Алгоритм Грэхема с предобработкой отсечением прямоугольником
•
Алгоритм Эндрю
•
Алгоритм быстрого построения оболочки
•
Модифицированный алгоритм Чена
•
Комбинированный алгоритм
Данные, полученные в результате тестирования, представлены в следующих графиках:
37
Равномерное распределение:
Рисунок 29. График времени работы алгоритмов на равномерном распределении исходного множества точек
38
Нормальное распределение:
Рисунок 30. График времени работы алгоритмов на нормальном распределении исходного множества точек
39
Лапласовское распределение:
Рисунок 31. График времени работы алгоритмов на лапласовском распределении исходного множества точек
40
Распределение точек на окружности:
Рисунок 32. График времени работы алгоритмов на распределении исходного множества точек на окружности
41
Кластерное распределение:
Рисунок 33. График времени работы алгоритмов на кластерном распределении исходного множества точек
Из приведенных результатов экспериментов видно, что комбинированный алгоритм, как
и ожидалось, показывает лучшее время на всех видах распределения исходного множества
точек.
42
5 Практическое применение алгоритмов построения выпуклых оболочек
5.1 Применение алгоритмов построения выпуклой оболочки на плоскости
Автором была разработана библиотека алгоритмов построения выпуклой оболочки на
плоскости и в пространстве, которая может быть применена в различных приложениях.
В настоящее время разработанная библиотека используется в коммерческой геоинформационной системе IndorGIS 5.0 для построения выпуклых оболочек на плоскости.
Ниже представлены примеры использования реализованной библиотеки в ГИС IndorGIS
5.0.
Рисунок 34. Иллюстрация применения библиотеки алгоритмов в ГИС IndorGIS 5.0
43
5.2 Практическое применение алгоритмов построения выпуклой оболочки в пространстве
Автором была разработана библиотека алгоритмов построения выпуклой оболочки на в
трехмерном пространстве, которая может быть применена в различных приложениях для построения выпуклых оболочек в трехмерном пространстве, а также для построения триангуляций Делоне.
В настоящее время разработанная библиотека находится на стадии тестирования и оптимизации.
Ниже представлены некоторые результаты работы библиотеки
1. Построение выпуклых оболочек в трехмерном пространстве
Рисунок 35. Иллюстрация выпуклых оболочек в трехмерном пространстве
44
2. Построение триангуляций Делоне
Рисунок 36. Иллюстрация применения алгоритмов построения выпуклых оболочек в трехмерном пространстве
для задачи построения триангуляции Делоне
45
Заключение
По результатам проведенной работы можно сделать следующие выводы:
1. Проанализированы существующие алгоритмы построения выпуклой оболочки в двухи трехмерном пространстве. Показаны их достоинства и недостатки.
2. Проанализированы способы эффективной практической реализации алгоритмов построения выпуклой оболочки.
3. Предложен подход с предобработкой исходного множества точек отсечением прямоугольником, позволяющий улучшить скорость существующих алгоритмов.
4. Предложена модификация алгоритма Чена, имеющая намного более высокую скорость работы, чем оригинальный алгоритм.
5. Результатами практического моделирования работы различных алгоритмов на различных видах исходных данных подтверждена лучшая скорость работы предложенных алгоритмов.
6. На основании проведенных экспериментов предложен комбинированный алгоритм,
показавший лучшую или близкую к лучшей экспериментальную скорость на всех задействованных в эксперименте классах распределения исходных данных.
7. Предложен подход с предобработкой исходного множества точек отсечением параллелепипедом, позволяющий улучшить скорость существующих алгоритмов.
8. Реализованы библиотеки процедур для построения выпуклых оболочек в двух- и
трехмерном пространстве.
9. Выполнено внедрение в ГИС IndorGIS 5.0 библиотеки разработанных алгоритмов построения выпуклой оболочки.
10. По результатам выполненной работы и смежным результатам опубликовано 2 печатных работы и подготовлена к печати 1 статья.
46
Список использованных источников
1.
Препарата Ф., Шеймос М. Вычислительная геометрия: Введение / Пер. с англ. – М.:
Мир, 1989. – 478 с.
2.
O’Rourke J. Computational geometry in C. – Cambridge University Press. – 1994. – 376 p.
3.
Chan T.M. Output-Sensitive Construction of Convex Hulls: Ph.D. thesis / Department of
Computer Science, University of British Columbia. – 1995. – 104 p.
4.
Jarvis A. On the identification of the convex hull of a finite set of points in the plane. // Information Processing Letters. – 1973. – Vol. 2. – pp.18–21.
5.
Graham R.L. An efficient algorithm for determining the convex hull of a finite planar set //
Information Processing Letters. – 1972. – Vol. 1. – pp. 132–133.
6.
Andrew A.M. Another efficient algorithm for convex hulls in two dimensions // Information
Processing Letters. – 1979. – Vol. 9. – Pp. 216–219.
7.
Preparata F.P., Hong S.J. Convex hulls of finite point sets in two and three dimensions //
Communications of the ACM. – 1977. – Vol. 2(20) . – Pp. 87–93.
8.
Eddy W. A new convex hull algorithm for planar sets // ACM Transactions on Mathematical Software. – 1977. – Vol. 3(4). – Pp. 398–403.
9.
Bykat A. Convex Hull of a Finite Set of Points in Two Dimensions // Information Processing Letters. – 1978. – Vol. 7. – Pp. 296–298.
10.
Kirkpatrick D.G., Seidel R. The ultimate planar convex hull algorithm? // SIAM Journal on
Computing. – 1986. – Vol. 15. – Pp. 287–299.
11.
Dobkin D.P., Kirkpatrick D.G. Fast detection of polyhedral intersection // Theoretical computer science. – 1983. – Vol. 27. – Pp. 241–253.
12.
Preparata F.P., Hong S.J. Convex hulls of finite sets of points in two and three dimensions //
Communications of the ACM. – 1977. – Vol. 20. – Pp. 87–93.
13.
Мирза Н.С., Чаднов Р.В. Триангуляция Делоне переменного разрешения // Материалы
XLII Международной студенческой конференции «Студент и научно-технический
прогресс». – Информационные технологии. – 2004. – С. 15–16.
14.
Computational Geometry Algorithms Library. – http://www.cgal.org.
15.
Chan T.M. Optimal output-sensitive convex hull algorithms in two and three dimensions //
Discrete & Computational geometry. – 1995.
16.
Chan T.M. Output-sensitive results on convex hulls, extreme points and related problems //
Proceedings of the 11th Annual ACM symposium on Computational Geometry. – 1995. –
Pp. 10–19.
17.
Чаднов Р.В., Мирза Н.С. Сравнительный анализ алгоритмов построения выпуклой
оболочки в двумерном пространстве // Материалы XLII Международной студенческой конференции «Студент и научно-технический прогресс». – Информационные
технологии. – 2004. – С. 15–16.
18.
Akl S.G., Toussaint G.T. A fast convex hull algorithm // Information processing letters. –
1978. – Vol. 7. – Pp 219-222.
47