Лекция 19 – Тонкостенные оболочки

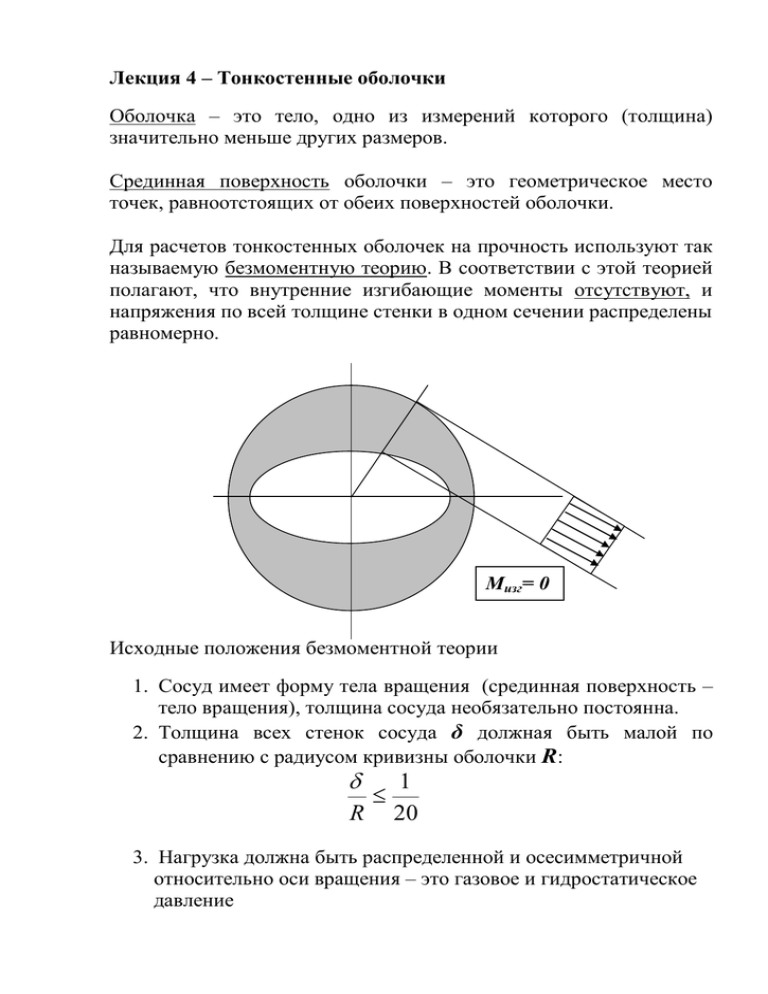
Лекция 4 – Тонкостенные оболочки
Оболочка – это тело, одно из измерений которого (толщина)
значительно меньше других размеров.
Срединная поверхность оболочки – это геометрическое место
точек, равноотстоящих от обеих поверхностей оболочки.
Для расчетов тонкостенных оболочек на прочность используют так
называемую безмоментную теорию. В соответствии с этой теорией
полагают, что внутренние изгибающие моменты отсутствуют, и
напряжения по всей толщине стенки в одном сечении распределены
равномерно.
Мизг= 0
Исходные положения безмоментной теории
1. Сосуд имеет форму тела вращения (срединная поверхность –
тело вращения), толщина сосуда необязательно постоянна.
2. Толщина всех стенок сосуда δ должная быть малой по
сравнению с радиусом кривизны оболочки R:

1

R 20
3. Нагрузка должна быть распределенной и осесимметричной
относительно оси вращения – это газовое и гидростатическое
давление
Уровень жидкости
Теория применима.
Теория неприменима.
Уравнение Лапласа
Рассмотрим тонкостенную оболочку, нагруженную внутренним
давлением. Двумя меридиональными сечениями и двумя
нормальными коническими сечениями вырежем элемент оболочки.
2
ρt
σm
dα
dφ
ρm
dφ/2
σm
ρm
σt
n
σt
q dφ
δ
n
dφ/2
σm
σt
ρt
dα
σt
q
dα/2
dα/2
n
3
σm
σmdφ
ρt
σm
dα
δρtdα
σt
dφ
σt
δ
-q n
ρtdαρmdφ
ρm
σtdα
δρmdφ
σm
Спроектируем все силы на направление нормали n:
 m d . . t d   t d . . m d  q t d . m d  0
Сначала сократим на dd , а затем все разделим на
В результате получаем известную формулу Лапласа:
m t q


 m t 
 t  m .
(*)
Отметим, что формула выведена для сосуда, имеющего форму
тела вращения. Поэтому, в самом общем случае, меридиональные
(осевые) σm и тангенциальные (окружные) σt напряжения будут
функцией координаты х точки на оси вращения, так как радиусы
кривизны ρm и ρt., толщина δ и внутреннее давление q могут
изменяться в зависимости от этой же координаты х.
4
Уравнение Лапласа содержит два напряжения σm и σt. Для
вычисления этих напряжений необходимо второе уравнения,
которое можно получить, спроектировав все силы, действующие на
элемент, на ось оболочки. Однако это удобнее делать не для
элемента, а для части оболочки, отсеченной нормальным
коническим сечением.
x
Отбросим верхнюю часть и рассмотрим равновесие нижней части:
σm φ
φ
φ
rx
σm
δ
x
Px
x
 m .2rx cos    Px  0
Px
m 
2rx cos  (**)
5
Вертикальная сила Px представляет собой сумму проекций на ось
всех сил, действующих на отсеченную часть оболочки. Для
вычисления этой силы полезно использовать две следующие
теоремы:
Теорема 1.
q
Px q   qFпр
Fпр
Px
x
Если на какую либо поверхность действует равномерно
распределенное давление
q , то независимо от формы
поверхности, проекция равнодействующей Px сил давления на
заданную ось x равна произведению давления q на площадь
проекции
Fпр
данной
поверхности
на
плоскость,
перпендикулярную заданной оси.
Теорема 2.
Px    abh
h
a
b
Px
Если на некоторую поверхность, например на дно, действует
давление жидкости с удельным весом γ, то вертикальная
составляющая Px сил давления жидкости равна весу жидкости в
объеме, расположенном над поверхностью.
6
Сфера
m t q


 m t 
R
 m  t  R

В силу сферической симметрии
m  t 
qR

Цилиндр
t
R
m
m

q
Px
m
m t q


 m t 
m 
;
Px
2rx cos 
m  
;
;
t  R
Px  qR 2
7
;
;
t 
m 
qR
2
qR

Конус
rx  xtg  
m
t
t
t
 tr
x
m
x
 
m t q


 m t 
x
Px
qxtg  
xtg  
 m   ; t  cos  ;  t   cos 
Px
2
m 
Px  q xtg  ;
2rx cos  ;
qxtg  
m 
2 cos 
При расчетах на прочность гибов и отводов трубопроводов
тепловых и атомных электростанций используют решения для
напряжений в торовой оболочке. Отводы и гибы соединяют с
прямыми трубами с помощью кривого участка трубы, который
рассматривают как часть тора.
8
Тор под внутренним давлением
q

t
0
Px
0
q

m
t
r
a
a
Для выделенного элемента тора

Px
t 
;
2rx sin  

2
rx  a  r sin  
Px  q rx  a2
qr 2a  r sin  
t 
2 a  r sin  
9
qr  t
m t q
 m  m (  )
 
 t
 m t  ;
qr
a  r sin  


m 
m


r
t
;
sin   ;
2
Окружное (тангенциальное) напряжение в торе, нагруженном
внутренним давлением, минимально на внешней образующей
(=3/2) и максимально на внутренней образующей(=/2).
При (=0 и (=) окружное напряжение равно напряжению в
прямой трубе с аналогичных размеров.
120
90
30
60
22.5
 t(  )
150
MPa
 m(  )
30
15
 t(  )
q r  2 a r sin (  )
2  a r sin (  )
7.5
180
0
0
MPa
210
330
240
300
270

Окружное напряжение
Меридиональное напряжение
10
 m(  )
q r
2 
Толстостенная труба (Формулы Лямэ)
tmax
tmin
b
t
a
r
r
rmax
qa 2  b 2 
 r r   2 2 1  2  
b  a  r  ; r m ax   q
qa 2  b 2 
 t r   2 2 1  2 
b a  r 

q b2  a 2
 t m ax  2 2
b a

;
;
 t m in
11
;
 r min  0
qa 2
z  2 2
b a
2qa 2
 2
b  a2
Преобразуем формулу для наиболее опасных окружных
напряжений
s
b R
2
;
s
a  R
2 ; s ba
Теперь она примет вид
qR qs


 t max s 

s
4R
;
Первый член этой формулы – окружные напряжения в
тонкостенной трубе – формула Лапласа.
qR
 t s  
s
Оценим ошибку вычислений, если напряжения в толстой трубе
будем вычислять по формуле Лапласа
 t maxs    t s 
 s  

 t maxs 
1
4R 2
1 2
s
Построим зависимость погрешности вычислений от отношения
толщины трубы к радиусу.
12
1
 ( s)
1
R
4
s
2
Погрешность вычислений, %
4
3
2
1
0
0
0.1
0.2
0.3
Отношение толщины трубы к радиусу
0.4
Погрешность вычислений напряжений
Как следует из приведенного графика, при увеличении отношения
толщины к радиусу до 0,4 , погрешность вычислений составляет
менее 4 %.
13