Нелинейные уравнения с одним неизвестным
advertisement

ГЛАВА 2
НЕЛИНЕЙНЫЕ УРАВНЕНИЯ
§ 1. Понятия и определения
1. Постановка задачи. Решение нелинейных уравнений с одним неизвестным является одной из важных математических задач, возникающих
в различных разделах физики, химии, биологии и других областях науки и
техники.
В общем случае нелинейное уравнение с одним неизвестным можно
записать в виде:
f ( x) = 0 ,
(2.1)
где f (x) – некоторая непрерывная функция аргумента x.
Всякое число x * , обращающее функцию f ( x) в нуль, т.е. при котором
f ( x * ) ≡ 0 , называется корнем уравнения (2.1). Если в точке x = x * наряду с
функцией обращаются в ноль и ее производные до (k − 1) порядка включительно, то число x * называют корнем k-й кратности. Однократный корень
также называют простым. В дальнейшем мы будем говорить именно о
простых корнях.
В зависимости от вида функции f ( x) нелинейные уравнения подразделяются на два класса – алгебраические и трансцендентные1.
Уравнение (2.1) называется алгебраическим, если функция f ( x) является алгебраической функцией. Алгебраическое уравнение всегда может
быть представлено в канонической форме:
f ( x) = a 0 + a1 x + a 2 x 2 + K + a n x n = 0 ,
(2.2)
где a0 , a1 , K, an – коэффициенты уравнения. Показатель n называют степенью алгебраического уравнения.
Если функция f ( x) содержит тригонометрические, показательные,
логарифмические и другие функции, не являющиеся алгебраическими, то
1
Трансцендентный (лат. transcendo – переступать): в философии – термин, означающий то, что запредельно по отношению к миру явлений и недоступно теоретическому
познанию; в математике – термин, обозначающий то, что не может быть вычислено алгебраическим путем или выражено алгебраически.
30
уравнение (2.1) называется трансцендентным. Примерами трансцендентных уравнений являются:
4 cos( x) + 0.3 x = 0 ;
2 x − 2 cos( x) = 0 ; lg( x + 5) = cos( x) .
Методы решения нелинейных уравнений делятся на прямые (аналитические, точные) и итерационные. Прямые методы позволяют записать решение в виде некоторого соотношения (формулы). При этом значения корней могут быть вычислены по этой формуле за конечное число арифметических операций. Подобные методы развиты для решения тригонометрических, логарифмических, показательных, а также простейших алгебраических уравнений.
Однако подавляющее большинство нелинейных уравнений, встречающихся на практике, не удается решить прямыми методами. Даже для
алгебраического уравнения выше четвертой степени не удается получить
аналитического решения в виде формулы с конечным числом арифметических действий. Во всех таких случаях приходится обращаться к численным
методам, позволяющим получить приближенные значения корней с любой
заданной точностью1.
При численном подходе задача о решении нелинейных уравнений
разбивается на два этапа: локализация (отделение) корней, т.е. нахождение
таких отрезков на оси x, в пределах которых содержится один единственный корень, и уточнение корней, т.е. вычисление приближенных значений
корней с заданной точностью.
2. Локализация корней. Для отделения корней уравнения (2.1) необходимо иметь критерий, позволяющий убедится, что, во-первых, на рассматриваемом отрезке [a, b] имеется корень, а, во-вторых, что этот корень
единственный на указанном отрезке.
f(b)
y = f(x)
Если функция f ( x) непрерывна на
отрезке [a, b] , а на концах отрезка
a
её значения имеют разные знаки
x
b
f (a ) ⋅ f (b) < 0 , то на этом отрезке
f(a)
расположен, по крайней мере, один
корень. Это условие (как видно из
рисунка 2.1) не обеспечивает единственности корня. Достаточным доРис. 2.1. Отделение корней. Функция
полнительным условием, обеспечиf(x) не монотонна на отрезке [a, b].
1
К таким случаям следует отнести и те, в которых, хотя и существуют формулы для
получения точного решения, но они столь громоздки, что использование приближенных методов оказывается более предпочтительным. Это относится, например, к алгебраическим уравнениям третьей и четвертой степени.
31
вающем единственность корня на отрезке [a, b] является требование монотонности функции на этом отрезке. В качестве признака монотонности
функции можно воспользоваться условием знакопостоянства первой производной f ′(x) .
Таким образом, если на отрезке [a, b] функция непрерывна и монотонна, а ее значения на концах отрезка имеют разные знаки, то на рассматриваемом отрезке существует один и только один корень. Заметим, что под
этот критерий не подпадают кратные корни уравнений, например, очевидный корень уравнения x 2 = 0 .
Воспользовавшись этим критерием можно отделить корни аналитическим способом, находя интервалы монотонности функции.
Отделение корней можно выполнить графически, если удается построить график функции y = f ( x) . В ряде случае бывает удобно заменить
уравнение f ( x) = 0 эквивалентным уравнением вида f1 ( x) = f 2 ( x) . Корни
этого уравнения определяются абсциссами точек пересечения графиков
функций y = f1 ( x) и y = f 2 ( x) .
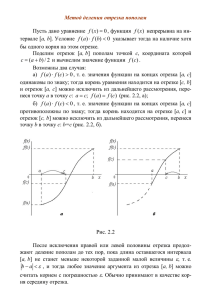
В качестве примера рассмотy
рим уравнение sin 2 x − ln x = 0 .
y = ln x
Переходя к эквивалентному урав1
нению sin 2 x = ln x построим графики функций
y = sin 2 x
и
π
1
y = ln x (рис. 2.2)
e
x
0
x*
Из графика видно, что уравнение содержит один корень, расположенный в интервале 1, π2 .
y = sin 2x
Отделение корней можно
также выполнить табличным споРис. 2.2. Графическое отделение корсобом. Допустим, что все интереней уравнения sin 2x – ln x = 0.
сующие нас корни уравнения (2.1)
находятся на отрезке [ A, B ] . Выбор этого отрезка (интервала поиска корней) может быть сделан,
y = f(x)
например, на основе анализа конh h
кретной физической или иной заA
дачи. Будем вычислять значения
x
B
f ( x) , начиная с точки x1 = A , двигаясь вправо с некоторым шагом h
(рис. 2.3). Как только обнаруживается пара соседних значений f ( x) ,
Рис. 2.3. Табличный способ
локализации корней.
имеющих разные знаки, так соот-
[ ]
32
ветствующие значения аргумента x можно считать границами отрезка, содержащего корень.
Надежность рассмотренного подхода к отделению корней уравнений
зависит как от характера функции f ( x) , так и от выбранной величины шага h. Действительно, если при достаточно малом значении h ( h << | B − A | )
на границах текущего отрезка [ x; x + h] функция f ( x) принимает значения
одного знака, то естественно ожидать, что уравнение f ( x) = 0 корней на
этом отрезке не имеет. Однако, это не всегда так: при несоблюдении условия монотонности функции f ( x) на отрезке [ x; x + h] могут оказаться кор-
+
x+h
x
–
x
x
x+h
x
–
–
а)
б)
Рис. 2.4.
ни уравнения (рис. 2.4а). Также несколько корней на отрезке [ x; x + h] могут оказаться и при выполнении условия f ( x) ⋅ f ( x + h) < 0 (рис. 2.4б).
Предвидя подобные ситуации, следует выбирать достаточно малые значения h.
Поскольку данный способ предполагает выполнение лишь элементарных арифметических и логических операций, количество которых может
быть велико при малых значениях h, для его реализации целесообразно использовать вычислительные возможности компьютера.
Отделяя таким образом корни, мы, по сути, получаем их приближенные значения с точностью до выбранного шага. Так, например, если в качестве приближенного значения корня взять середину отрезка локализации, то абсолютная погрешность этого значения не будет превосходить
половины шага поиска (h/2). Уменьшая шаг в окрестности каждого корня,
можно, в принципе, повысить точность отделения корней до любого наперед заданного значения. Однако такой способ требует большого объема
вычислений. Поэтому при проведении численных экспериментов с варьированием параметров задачи, когда приходится многократно осуществлять
поиск корней, подобный метод не годится для уточнения корней и используется только для отделения (локализации) корней, т.е. определения начальных приближений к ним. Уточнение корней проводится с помощью
других, более экономичных методов.
33
3. Уточнение корней. На данном этапе задача состоит в получении
приближенного значения корня, принадлежащего отрезку [a,b] , с заданной
точностью (погрешностью) ε. Это означает, что вычисленное значение
x должно отличаться от точного x ∗ не более чем на величину ε:
корня ~
| x∗ − ~
x |≤ ε .
Процедура численного определения приближенных значений корней
нелинейных уравнений, как правило, состоит в выборе начального приближения к корню x0 ∈ [a, b] и вычислении по некоторой формуле последующих приближений x1 , x2 и т.д. Каждый такой шаг называется итерацией (от латинского iteratio – повторение), а сами методы уточнения –
итерационными методами. В результате итераций получается последовательность приближенных значений корня x0 , x1 ,K,xk ,K , которая называется итерационной последовательностью. Если эти значения с ростом k
стремятся к точному значению корня x ∗ :
lim {xk } = x ∗ ,
k →∞
(2.3)
то говорят, что итерационный процесс сходится.
Сходимость итерационного процесса означает, что погрешность каждого последующего приближения должна быть меньше погрешности предыдущего приближения, т.е. погрешность приближенных значений с каждым шагом должна уменьшаться:
| x ∗ − x k +1 | < | x ∗ − x k |
В общем случае это неравенство можно представить в виде:
| x ∗ − x k +1 | < q | x ∗ − x k |α ,
34
(2.4)
где q > 0 и α ≥ 1 – некоторые числа, значения которых определяются методом уточнения корня. От значений q и α зависит насколько с каждым
шагом уменьшается погрешность приближенных значений и, соответственно, насколько быстро можно получить приближенное значение с заданной точностью. Главным показателем скорости сходимости метода является значение α, называемое порядком сходимости. При α = 1 погрешность
с каждым шагом убывает линейно, в этом случае говорят о линейной сходимости. Если α > 1 , то говорят, что имеет место сверхлинейная сходимость.
35
§ 2. Методы уточнения корней
1. Метод половинного деления (бисекции, дихотомии)
Считаем, что отделение корней уравнения (2.1) проведено и на отрезке [a, b] расположен один корень, который необходимо уточнить с погрешностью ε. В качестве начального приближения корня принимаем
f(b)
середину
этого
отрезка:
f(с0 )
c0 = (a + b) / 2 (рис. 2.5). Затем исследуем значение функции f ( x) на
a
концах отрезков [a, c0 ] и [c0 , b] . Тот
x
с0
с1
b
из отрезков, на концах которого
f ( x) принимает значения разных
f(a)
знаков, содержит искомый корень;
поэтому его принимаем в качестве
нового отрезка [a1 , b1 ] (на рис. 2.5
Рис. 2.5. Метод половинного деления.
это отрезок [a, c0 ] ). Вторую половину отрезка [a, b] , на которой f ( x) не
меняет знак, отбрасываем. В качестве следующего приближения корня
принимаем середину нового отрезка c1 = (a1 + b1 ) / 2 и т.д. Таким образом,
k-е приближение вычисляется как
ck =
a k + bk
.
2
(2.5)
После каждой итерации отрезок, на котором расположен корень, уменьшается вдвое, а после k итераций в 2 k раз:
bk − a k =
b−a
2k
.
(2.6)
Прекратить итерационный процесс следует, когда будет достигнута
заданная точность, т.е. при выполнении условия
| x ∗ − ck | < ε .
(2.7)
Поскольку корень x ∗ принадлежит отрезку [ak , bk ] , а ck – середина этого
отрезка, то величина | x ∗ − c k | всегда будет меньше половины длины отрезка [ak , bk ] (см. рис. 2.5), т.е.
36
| x ∗ − ck | <
| bk − a k |
.
2
(2.8)
Следовательно, условие (2.7) будет выполнено, если
| bk − a k | < 2ε .
(2.9)
Таким образом, итерационный процесс нужно продолжать до тех пор,
пока не будет выполнено условие (2.9).
В отличие от большинства других методов уточнения, метод половинного деления сходится всегда, т.е. обладает безусловной сходимостью.
Кроме этого он чрезвычайно прост, поскольку требует лишь вычисления
значений функции f ( x) и, поэтому применим для решения любых уравнений.
Однако метод половинного деления довольно медленный. С каждым
шагом погрешность приближенного значения уменьшается в два раза, т.е.
| x ∗ − c k +1 | ≤
1 ∗
| x − ck | ,
2
(2.10)
поэтому данный метод является методом с линейной сходимостью.
Вычислим количество итераций N, требуемое для достижения заданной точности ε. Пользуясь выражением (2.6) можно выяснить для каких
значений k будет выполнено условие (2.9), и взять в качестве N наименьшее из таких k:
k > log 2
b−a
,
2ε
b−a⎞
⎛
N = int⎜ log 2
⎟ + 1,
2ε ⎠
⎝
(2.11)
где int( x) – целая часть числа x. Например, при b − a = 1 и ε = 10 −6 получим N = 19 .
¾ З а м е ч а н и е . При реализации метода следует учитывать, что
функция f ( x) вычисляется с некоторой абсолютной погрешностью ∆f .
Вблизи корня значения функции f ( x) малы по абсолютной величине и могут оказаться сравнимы с погрешностью ее вычисления. Другими словами,
при подходе к корню мы можем попасть в полосу шумов 2∆f и дальнейшее уточнение корня окажется невозможным. Поэтому целесообразно задать ширину полосы шумов и прекратить итерационный процесс при попадании в нее. Если принять ∆f = ε , то итерационный процесс можно за-
37
вершать, когда значение функции f ( x) после k-й итерации станет меньшим по модулю ε., т.е.
f (c k ) < ε .
(2.12)
Также необходимо иметь ввиду, что при уменьшении интервала [a, b]
увеличиваются погрешности вычисления его длины b − a за счет вычитания близких чисел.1
2. Метод хорд
Рассматриваемый метод так же, как и метод половинного деления,
предназначен для уточнения корня на интервале [a,b] , на концах
B
которого функция f ( x) принимаB1
ет значения разных знаков. Очередное приближение в отличие от
метода половинного деления беa
рем не в середине отрезка, а в точx1 x0
x
b
ке x0 , где пересекает ось абсцисс
прямая линия (хорда), проведенA
ная через точки А и В (рис. 2.6).
Запишем уравнение прямой,
Рис. 2.6. Метод хорд.
проходящей через точки А и В:
y − f (a)
x−a
.
=
f (b) − f (a) b − a
Для точки пересечения прямой с осью абсцисс ( x = x0 , y = 0 ) получим
уравнение
x0 = a −
b−a
f (a) .
f (b) − f (a)
(2.13)
В качестве нового интервала для продолжения итерационного процесса выбираем тот из двух [a, x0 ] и [ x0 , b] , на концах которого функция f (x)
принимает значения разных знаков. Для рассматриваемого случая (рис.
2.6) выбираем отрезок [a, x0 ] , так как f (a) ⋅ f ( x0 ) < 0 . Следующая итерация состоит в определении нового приближения x1 как точки пересечения
хорды AB1 с осью абсцисс и т.д.
1
Здесь и далее символом будем обозначать конец замечания.
38
Заканчиваем процесс уточнения корня, когда расстояние между очередными приближениями станет меньше заданной точности, т.е.
xk +1 − xk < ε
(2.14)
или при выполнении условия (2.12).
¾ З а м е ч а н и е . Метод половинного деления и метод хорд очень похожи, в частности, процедурой проверки знаков функции на концах отрезка. При этом второй их них в ряде случаев дает более быструю сходимость
итерационного процесса. Однако в некоторых случаях метод хорд может
сходится существенно медленнее метода половинного деления. Такая ситуация показана на рис. 2.7. Оба рассмотренных метода не требуют знания дополнительной информации о
функции f (x) . Например, не требуется, чтобы функция была дифференцируема. Даже для разрывных
a
x*
функций рассмотренные методы обx
b
ладают гарантированной сходимостью. Более сложные методы уточнения корня используют дополнительную информацию о функции
Рис. 2.7. О сходимости метода хорд
f (x) , прежде всего свойство дифференцируемости. Как результат они обычно обладают более быстрой сходимостью, но в то же время, применимы для более узкого класса функций,
и их сходимость не всегда гарантирована. Примером такого метода служит
метод Ньютона.
3. Метод Ньютона (метод касательных)
Пусть нам известно начальное приближение к корню x0 (вопрос выбора начального приближение будет подробно рассмотрен ниже). Проведем в этой точке касательную к кривой y = f (x) (рис. 2.8). Эта касательная
пересечет ось абсцисс в точке x1 , которую будем рассматривать в качестве
следующего приближения. Значение x1 легко найти из рисунка:
tg α =
f ( x0 )
= f ′( x0 ) ,
x0 − x1
выражая отсюда x1 , получим
39
f(x0)
x1 = x0 −
f ( x0 )
.
f ′( x0 )
Аналогично могут быть найдены и
следующие приближения. Формула
для k+1-го приближения имеет вид
x k +1 = x k −
f ( xk )
,
f ′( xk )
x*
α
x1
x0
x
k = 0,1, 2, ...
(2.15)
Рис. 2.8. Метод Ньютона.
Из формулы (2.15) вытекает условие применимости метода: функция f (x)
должна быть дифференцируемой и f ′(x) в окрестности корня не должна
менять знак.
Для окончания итерационного процесса могут быть использованы условия (2.12) или (2.14).
¾ З а м е ч а н и е 1 . В методе Ньютона, в отличие от предыдущих методов, не обязательно задавать отрезок [a, b], содержащий корень уравнения, а достаточно найти некоторое начальное приближение корня x0 .
¾ З а м е ч а н и е 2 . Формула метода Ньютона может быть получена и
из других соображений. Зададимся некоторым начальным приближением
корня x0 ∈ [a, b] . Заменим функцию f(x) в окрестности точки x0 отрезком
ряда Тейлора:
f ( x) ≈ f ( x0 ) + ( x − x0 ) f ′( x0 ) ,
и вместо нелинейного уравнения f ( x) = 0 решим линеаризованное уравнение
f ( x0 ) + ( x − x0 ) f ′( x0 ) = 0
рассматривая его решение как следующее (первое) приближение к искомому значению корня. Решение этого уравнение очевидно:
x1 = x0 −
f ( x0 )
f ′( x0 )
Повторяя это процесс приходим к формуле Ньютона (2.15).
40
Сходимость метода Ньютона. Выясним основные условия сходимости последовательности значений {xk } , вычисляемых по формуле (2.15), к
корню уравнения (2.1). Предполагая, что f (x) дважды непрерывно диффе-
ренцируема, разложим f (x ∗ ) в ряд Тейлора в окрестности k-го приближения
( x ∗ − xk ) 2
f ( x ) = f ( xk ) + ( x − xk ) f ′( xk ) +
f ′′( xk ) = 0 .
2
∗
∗
Разделив последнее соотношение на − f ′( xk ) и перенеся часть слагаемых из левой части в правую, получим:
⎡
f ( x k ) ⎤ ∗ 1 f ′′( x k )
−x =
( xk − x ∗ ) 2 .
x
−
k
⎢
⎥
2 f ′( x k )
f ′( x k ) ⎦
⎣
Учитывая, что выражение в квадратных скобках согласно (2.15) равно
xk +1 , переписываем это соотношение в виде
xk +1 − x ∗ =
1 f ′′( xk )
( xk − x ∗ ) 2 .
2 f ′( xk )
Отсюда
| xk +1 − x ∗ | =
1 | f ′′( xk ) |
| xk − x ∗ | 2 .
2 | f ′( xk ) |
(2.16)
1 M2
| xk − x ∗ |2 ,
2 m1
(2.17)
Из (2.16) следует оценка
| xk +1 − x ∗ | ≤
где M 2 = max f ′′( x) , m1 = min f ′( x) .
[a, b]
[ a , b]
Очевидно, что ошибка убывает, если
1 M2
x0 − x ∗ < 1 .
2 m1
(2.18)
41
Полученное условие означает, что сходимость зависит от выбора начального приближения.
Оценка (2.17) характеризует скорость убывания погрешности для метода Ньютона: на каждом шаге погрешность пропорциональна квадрату
погрешности на предыдущем шаге. Следовательно, метод Ньютона обладает квадратичной сходимостью.
Выбор начального приближения в методе Ньютона. Как следует из
условия (2.18) сходимость итерационной последовательности, получаемой
в методе Ньютона, зависит от выбора начального приближения x0 . Это
можно заметить и из геометрической интерпретации метода. Так, если в
качестве начального приближения взять точку x0′ (рис. 2.9), то на сходимость итерационного процесса рассчитывать не приходится.
x0′
x*
x0
x1′
x2′
x
Рис. 2.9.
Если же в качестве начального приближения выбрать точку x0 , то получим сходящуюся последовательность.
В общем случае, если задан отрезок [a, b], содержащий корень, и известно, что функция f (x) монотонна на этом отрезке, то в качестве начального приближения x0 можно выбрать ту границу отрезка [a, b], где
совпадают знаки функции f (x) и второй производной f ′′(x) . Такой выбор
начального приближения гарантирует сходимость метода Ньютона при условии монотонности функции на отрезке локализации корня.
4. Модифицированный метод Ньютона
Рассмотренный выше метод Ньютона требует вычисления производной f ′(x) на каждом шаге. В некоторых случаях это может существенно
снизить эффективность метода (в смысле затрат машинного времени). Поэтому в тех случаях, когда вычисление производной сопряжено с существенными затратами машинного времени, используют модифицированный
метод Ньютона, в котором производная f ′(x) вычисляется только в точке
начального приближения x0 :
42
xk +1 = xk −
f ( xk )
.
f ′( x0 )
(2.19)
5. Метод секущих
Еще одна модификация метода Ньютона связана с приближенным вычисление производной f ′(x) в окрестности точки xk по формуле
f ′( xk ) ≈
f ( xk ) − f ( xk −1 )
.
xk − xk −1
Подставляя это выражение в формулу Ньютона (2.15), приходим к
формуле
xk +1 = xk −
f ( xk )( xk − xk −1 )
, k = 1, 2, ... ,
f ( xk ) − f ( xk −1 )
(2.20)
которая определяет метод секущих. Название метода связано с его геометрической интерпретацией (см. рис. 2.10). Секущая, проведенная через точки ( x0 , f ( x0 ) ) и ( x1 , f ( x1 ) ) , пересекает ось абсцисс в точке x2 , значение
которой определяется формулой (2.20).
Для того, чтобы начать итерационный процесс в методе секущих необходимо задать два начальных приближения: нулевое x0 и первое x1 . На
практике, как правило, поступают следующим образом: нулевое приближение выбирают аналогично выбору начального приближения в методе
Ньютона, а в качестве первого приближения выбирают величину
f(x0)
x1 = x0 ± ε , где ε – заданная погрешность. Эти значения используются для нахождения последующего (второго) приближения x2 по
f(x1)
формуле (2.20). Затем, значения x1
x*
и x2 используют для определения
x2 x1
x
x0
третьего приближения x3 и т.д.
Альтернативно, в качестве нулевого и первого приближений могут
Рис. 2.10. Метод секущих.
быть выбраны границы отрезка локализации корня, если они извест-
43
ны. В этом случае первая итерация метода секущий даст результат, аналогичный методу хорд. Для завершения итерационного процесса можно воспользоваться условием (2.14).
Метод секущих несколько уступает методу Ньютона в скорости сходимости, однако он не требует вычисления производной f ′(x) и поэтому
оказывается особенно полезным в тех случаях, когда получение аналитического выражения для производной f ′(x) затруднено или невозможно,
например, если функции f (x) получена в ходе численных расчетов, а не
задана аналитически.
По алгоритму метод секущих близок к методу хорд, однако в отличие
от последнего начальные приближения в методе секущих могут располагаться как с разных сторон от корня, так и с одной стороны; кроме того
при уточнении корня не проверяются знаки функции f (x) .
6. Метод простых итераций
Теперь рассмотрим более общий итерационный метод уточнения корней. Представим исходное уравнение f ( x) = 0 в виде
x = ϕ (x) .
(2.21)
О том как преобразовать исходное уравнение к виду (2.21) буден рассказано ниже.
Пусть нам известно начальное приближение к корню x0 ( x0 ∈ [a, b] ).
Подставив его в правую часть уравнения (2.21) получим новое приближение x1 = ϕ ( x0 ) , затем аналогичным образом получим x2 = ϕ ( x1 ) и так далее,
xk +1 = ϕ ( xk ) , k = 0,1,.... .
(2.22)
Оказывается, что при определенных свойствах функции ϕ (x) последовательность {x1 , x2 , ..., xk , ...} , определяемая по формуле (2.22), сходится
к корню уравнения f ( x) = 0 . Необходимо установить при каких условиях
итерационный процесс (2.22) будет сходящимся.
В начале рассмотрим графически процесс получения приближений в
методе простых итераций (рис. 2.11). При решении уравнения (2.21) необходимо отыскать точку пересечения кривой y = ϕ (x) и прямой y = x . На
рисунке 2.11, (а) изображена некоторая кривая y = ϕ (x) , которая может
представлять собой любую функцию, но сейчас для нас важно то обстоятельство, что производная этой функции в окрестности корня положительна и меньше 1. Пусть x = x * – корень уравнения, который, естественно,
предполагается неизвестным. Выберем начальное приближение в точке x0 .
44
Следующее приближении x1 , в соответствии с (2.22), будет равно ϕ ( x0 ) .
Для того, чтобы отобразить x1 на графике можно провести через точку
(x0 , f ( x0 )) прямую, параллельную оси OX, до пересечения с прямой y = x ,
а затем в точке пересечения этих прямых опустить перпендикуляр на ось
OX, который и отметит положение точки x1 . Аналогично получаются все
последующие приближения. Из рисунка видно, что они сходятся к корню.
Напомним, что для рассмотрения мы взяли функцию, производная которой
положительна и меньше 1.
y
y
y=x
y =ϕ(x)
y =ϕ(x)
0
x0
y=x
x2 x*
x1
x
0
x* x0
а)
б)
y
y
x
x2
x1
y =ϕ(x)
y=x
y=x
y =ϕ(x)
0
*
x0 x2 x
x1
в)
x
0 x2
*
x0 x
x1
x
г)
Рис. 2.10. Метод простых итераций. а) односторонний сходящийся процесс; б) односторонний расходящийся процесс; в) двухсторонний сходящийся процесс; г) двухсторонний расходящийся процесс.
45
Рассмотрим теперь другую функцию y = ϕ (x) , производная которой
отрицательна, но меньше 1 по абсолютному значению. Этот случай изображен на рисунке 2.11, в. Последовательные приближения также сходятся
к корню, но на этот раз каждое последующее приближение находится с
противоположной стороны от корня. В то время как в первом случае все
последовательные приближения находились с одной стороны от корня.
Наконец, рассмотрим случай, когда производная функции y = ϕ (x)
больше 1 (рис. 2.11, б) и меньше -1 (рис. 2.11, г). В обоих случаях каждое
последующее приближение отстоит дальше от корня, т.е. итерационный
процесс расходится. Из сказанного выше можно предположить, что итерационный процесс, определяемый формулой (2.22) сходится при условии,
что производная ϕ ′(x) меньше 1 по абсолютной величине.
Математически условие сходимости можно установить следующим
образом. Представим k-е и (k+1)-е приближения в форме
x k = x ∗ + ε k , x k +1 = x ∗ + ε k +1 ,
где ε k и ε k +1 – отклонения приближений от корня.
Функцию ϕ (x) вблизи точки x ∗ приближенно заменим первыми двумя членами ряда Тейлора. Тогда итерационная формула (2.22) примет вид
x ∗ + ε k +1 ≈ ϕ ( x ∗ ) + ε k ϕ ′( x ∗ ) ,
но поскольку x ∗ является корнем уравнения, то первые слагаемые в правой и левой частях этого выражения тождественно равны и, следовательно
ε k +1 ≈ ε k ϕ ′( x ∗ ) .
Для сходимости итерационного процесса необходимо, чтобы погрешность
на каждом шаге убывала
| ε k +1 | < | ε k | ,
откуда следует, что в окрестности корня должно выполняться условие
ϕ ′( x) < 1.
(2.23)
Таким образом, для того чтобы итерационный процесс (2.22) был сходящимся, необходимо, чтобы абсолютная величина производной ϕ ′(x) в
окрестности корня была меньше единицы. Если это условие выполняется
46
на отрезке [a, b] на котором локализован корень, то в качестве начального
приближения можно взять любую точку из этого отрезка x0 ∈ [a, b] . Скорость сходимости зависит от абсолютной величины производной | ϕ ′( x) | :
чем меньше | ϕ ′( x) | вблизи корня, тем быстрее сходится процесс.
Преобразование уравнения к итерационному виду. Переход от
уравнения (2.1) к уравнению в итерационной форме (2.21) можно осуществить различными способами в зависимости от вида функции f (x) . При таком переходе необходимо построить функцию ϕ (x) так, чтобы выполнялось условие сходимости (2.23).
В качестве примера рассмотрим уравнение x 3 − x − 1 = 0 , один из корней которого расположен в интервале [1, 2]. Преобразуем это уравнение к
виду (2.21) следующим образом: x = x 3 − 1 . Проверим условие сходимости
для средней точки интервала локализации x = 1.5 :
ϕ ( x) = x 3 − 1 , ϕ ′( x) = 3 x 2 , | ϕ ′(1.5) | = 6.75 >1.
Очевидно, что условие сходимости (2.23) не выполнено. Преобразуем
уравнение к итерационному виду другим способом: x = 3 x + 1 и вновь проверим условие сходимости:
ϕ ( x) = 3 x + 1 , ϕ ′( x) =
1
3 ( x + 1) 2 / 3
, | ϕ ′(1.5) | = 0.133 < 1.
Видно, что в этом случае условие сходимости выполнено.
Теперь рассмотрим один из общих алгоритмов перехода от уравнения
f ( x) = 0 к уравнению x = ϕ (x) . Умножим левую и правую части уравнения f ( x) = 0 на произвольную константу τ ≠ 0 и добавим к обеим частям
неизвестное x. При этом корни исходного уравнения не изменятся
x + τ ⋅ f ( x) = x + 0 ⋅ τ
или
x = x + τ f (x) .
(2.24)
Уравнение (2.24) эквивалентно уравнению (2.21) с функцией
ϕ ( x) = x + τ f ( x) . Произвольный выбор константы τ позволяет обеспечить
выполнение условия сходимости (2.23). Поскольку в данном случае
ϕ ′( x) = 1 + τ f ′( x) , значение τ следует выбирать, так чтобы в окрестности
корня выполнялось условие
47
ϕ ′( x) = 1 + τ f ′( x) < 1.
(2.25)
Желательно выбрать величину τ такой, чтобы − 1 < ϕ ′( x) < 0 , тогда сходимость будет двухсторонней (рис. 2.11, в). В этом случае в качестве критерия окончания итерационного процесса можно использовать соотношение
(2.14).
¾ З а м е ч а н и е . При сходимости последовательных приближений к
корню с разных сторон, что имеет место при ϕ ′( x) < 0 в окрестности корня
(рис. 2.10, в), величина xk +1 − xk превосходит истинную погрешность, т.е.
| x k +1 − x k | > | x k +1 − x ∗ | , и критерий окончания итерационного процесса
(2.14) является вполне объективным. Если же ϕ ′( x) > 0 , то сходимость к
корню носит односторонний характер (рис. 2.11, а), и условие
xk +1 − xk ≤ ε может выполниться гораздо раньше нужного требования
| x k +1 − x ∗ | ≤ ε . В этом случае контроль достигнутой точности лучше осуществлять по проверке неравенства
1
| x k +1 − xk | ≤ ε ,
1− q
где q = max | ϕ ′( x) | .
[ a, b]
Наибольшую скорость сходимости в методе простых итераций получим при ϕ ′( x) = 0 . Этого можно добиться, если выбрать параметр τ зависящим от x в виде
1
.
(2.26)
τ ( x) = −
f ′( x)
При этом итерационная формула (2.22) переходит в формулу Ньютона
xk +1 = xk − f ( xk ) f ′( xk ) .
Таким образом, метод Ньютона можно трактовать как частный случай
метода простых итераций, обладающий максимальной скоростью сходимости.
7. Метод Мюллера
Идея метода Мюллера состоит в приближенной замене функции f (x)
интерполяционным полиномом второй степени (параболой), построенным
по трем точкам xk −2 , xk −1 , xk , и нахождением абсциссы точки пересечения
48
этой параболы с осью OX, т.е. решением квадратного уравнения. Иными
словами в методе Мюллера используется не линейная аппроксимация, как
в методах хорд, секущих и Ньютона, а квадратичная.
Расчетные формулы метода следующие:
q=
xk − xk −1
,
xk −1 − xk −2
A = qf ( x k ) − q (1 + q ) f ( x k −1 ) + q 2 f ( x k −2 ) ,
B = ( 2q + 1) f ( x k ) − (1 + q ) 2 f ( x k −1 ) + q 2 f ( x k −2 ) ,
C = (1 + q) f ( xk ) ,
⎞
⎛
2C
⎟.
xk +1 = xk − ( xk − xk −1 )⎜⎜
⎟
2
⎝ B ± B − 4 AC ⎠
(2.27)
Знак перед корнем выбирается так, чтобы абсолютное значение знаменателя было максимальным.
Метод Мюллера обладает сверхлинейной сходимостью с порядком
сходимости ≈ 1.8 .
8. Метод Риддерса
Метод Риддерса1 является модификацией рассмотренного ранее метода хорд и применяется в тех случаях, когда известен отрезок локализации
корня. Приведем расчетные формулы метода Риддерса без вывода:
x k +1 = β + ( β − x k −1 )
где β =
sign[ f ( x k −1 ) − f ( x k )] f ( β )
2
f ( β ) − f ( x k −1 ) f ( x k )
,
(2.28)
x k −1 + x k
, а функция sign(x) определена следующим образом:
2
⎧− 1, при x < 0
⎪
sign( x) = ⎨ 0, при x = 0 .
⎪ 1, при x > 0
⎩
Несомненным достоинством метода Риддерса является, тот факт, что
определяемые по формуле (2.28) последовательные приближения корня,
также как и в методе хорд, всегда располагаются внутри отрезка локализа-
1
C.J.F. Ridders, IEEE Transactions on Circuits and Systems, vol. CAS-26, p. 979. (1979)
49
ции, и при этом метод обладает сверхлинейной сходимостью с порядком
сходимости 2 .
9. Методы Дэккера и Брэнта
Методы
10. Методы решения алгебраических уравнений. Все рассмотренные выше методы уточнения корней нелинейных уравнений одинаково
пригодны как для трансцендентных, так и для алгебраических уравнений.
В то же время существуют методы, учитывающие специфику решаемой
задачи. Рассмотрим кратко два таких метода.
Метод Лагерра основывается на следующих соотношениях для полиномов
Pn ( x) = ( x − x1 )( x − x2 )K ( x − xn )
ln Pn ( x) = ln x − x1 + ln x − x2 + K + ln x − xn
d ln Pn ( x)
dx
−
d 2 ln Pn ( x)
dx 2
=
P′
1
1
1
+
+L +
= n ≡G
x − x1 x − x 2
x − xn Pn
2
⎡ Pn′ ⎤
Pn′′
−
≡H
L
=
+
+
+
=
⎥
⎢
Pn
( x − x1 ) 2 ( x − x2 ) 2
( x − xn ) 2 ⎣ Pn ⎦
1
1
1
Предполагают, что корень x1 , который мы ищем, находится на расстоянии a от текущего приближения, в то время как все другие корни находятся на расстоянии b: x − x1 = a ; x − xi = b , i = 2, 3,...., n .
Тогда с учетом рассмотренных соотношений для полиномов можно
записать
1 n −1
1 n −1
+ 2 =H.
+
=G и
a
b
a2
b
Выражая из этих соотношений а, получим
a=
n
2
G ± (n − 1)(nH − G )
.
Знак перед корнем выбирается таким образом, чтобы знаменатель имел
наибольшее значение.
50
Метод сопровождающей матрицы. В основе этого метода лежит то
факт, что собственные значения квадратной матрицы А, т.е. такие числа λ,
для которых выполняется равенство Ax = λx , могут быть определены как
корни характеристического полинома P ( x) = det( A − λI ) = 0 .
Можно показать, что для матрицы
⎛ a n−1
⎜−
⎜ an
⎜ 1
A=⎜
⎜ 0
⎜ M
⎜
⎝ 0
−
a n−2
an
0
L
a1
an
0
1
L
0
0
L
1
L −
−
a0 ⎞
⎟
an ⎟
0 ⎟
⎟,
0 ⎟
M ⎟
⎟
0 ⎠
называемой сопровождающей матрицей, характеристическим полиномом
n
будет являться полином общего вида P( x) = ∑ ai x i . Таким образом, задаi =0
чу поиска корней полинома можно свести к задаче нахождения собственных значений сопровождающей матрицы.
Вопросы для самоконтроля
1. Из каких этапов состоит численное решение нелинейных уравнений и в
чем они заключаются?
2. В чем заключается отличие метода хорд от метода половинного деления
и что в них общего?
3. Почему в методе хорд не применимо условие окончания итерационно
процесса, использующееся в методе половинного деления?
4. Каковы условия применимости метода Ньютона?
5. Как выбирается начальное приближение в методе Ньютона?
6. Каковы условия сходимости итерационной последовательности в методе простых итераций?
7. Какое условие является критерием достижения заданной точности в методах Ньютона и простых итераций?
51