Тема 5. Проверка статистических гипотез о числовых значениях
advertisement
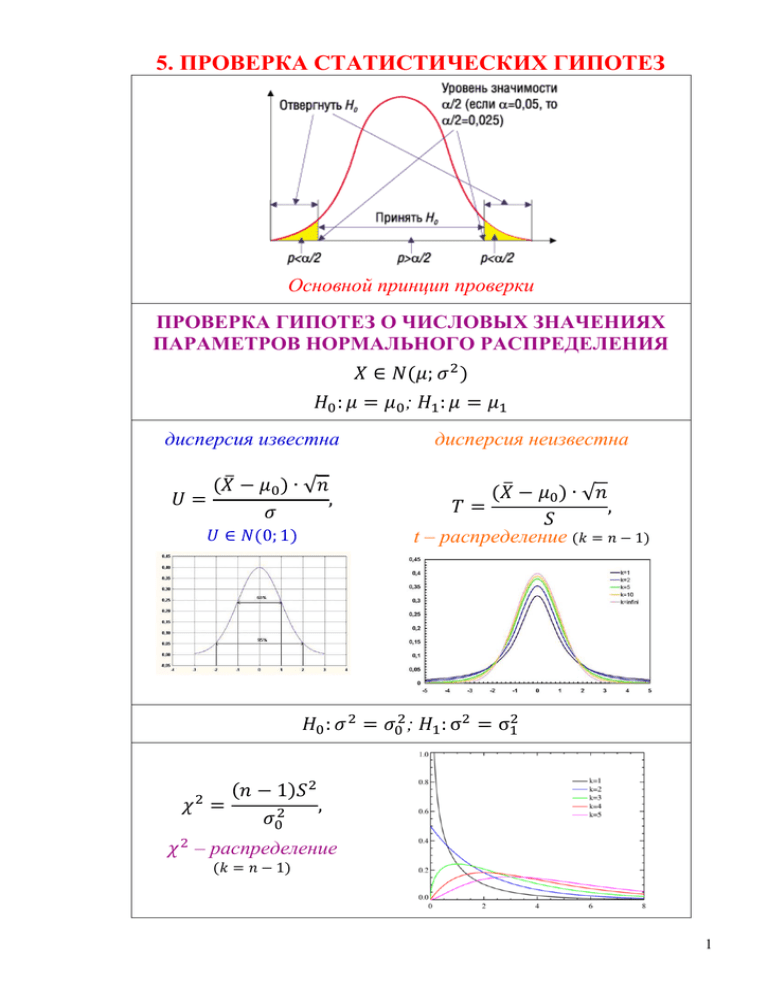
5. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ Основной принцип проверки ПРОВЕРКА ГИПОТЕЗ О ЧИСЛОВЫХ ЗНАЧЕНИЯХ ПАРАМЕТРОВ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ ; дисперсия известна ̅ дисперсия неизвестна √ ̅ √ t – распределение ; – распределение 1 Практическое занятие №5 ПРОВЕРКА ГИПОТЕЗ О ЧИСЛОВЫХ ЗНАЧЕНИЯХ ПАРАМЕТРОВ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ Основные этапы проверки Под статистической гипотезой понимают всякое высказывание о генеральной совокупности (случайной величине), проверяемое по выборке (по результатам наблюдений). Как правило, статистическая гипотеза – это предположение о значении параметров закона распределения (параметрическая) или его виде (непараметрическая). Не располагая сведениями о всей генеральной совокупности, высказанную гипотезу сопоставляют, по определенным правилам, с выборочными данными и делают вывод о том, можно принять гипотезу или нет. Процедура сопоставления высказанной гипотезы с выборкой называется проверкой гипотезы. Рассмотрим этапы проверки гипотезы и используемые при этом понятия. Этап 1. Проверяемую гипотезу обычно называют нулевой (или основной) и обозначают Н0. Наряду с нулевой гипотезой рассматривают альтернативную (или конкурирующую) гипотезу Н1, являющуюся логическим отрицанием Н0. Нулевая и альтернативная гипотезы представляют собой две возможности выбора, осуществляемого в задачах проверки статистических гипотез. По выборке будет принято решение о справедливости для генеральной совокупности либо гипотезы Н0, либо гипотезы Н1. Этап 2. Задаются вероятностью α, которую называют уровнем значимости. Введем ее смысловое назначение. Решение о том, можно ли считать высказывание Н0 справедливым для генеральной совокупности, принимается по выборочным данным (т.е. по ограниченному ряду наблюдений), следовательно, это решение может быть как правильным, так и ошибочным. При проверке любой статистической гипотезы возможны варианты: гипотеза Н0 верна и ее принимают (правильное решение); гипотеза Н0 не верна и ее отвергают, принимая гипотезу Н1 (правильное решение); гипотеза Н0 верна, но ее отвергают согласно правилу проверки (неправильное решение) - это ошибка первого рода; гипотеза Н0 не верна, но ее принимают согласно правилу проверки (неправильное решение) – это ошибка второго рода. Уровень значимости α – это вероятность ошибки первого рода, т.е. вероятность того, что будет принята гипотеза Н1, если на самом деле для генеральной совокупности верна гипотеза Н0. Вероятность α задается заранее малым числом, поскольку это вероятность ошибочного заключения, при этом обычно используют некоторые стандартные значения: 0,05; 0,01; 0,005; 0,001. Вероятность ошибки второго рода обозначают β – это вероятность того, что будет принята гипотеза Н0, если на самом деле верна гипотеза Н1. Вероятность не совершить ошибку второго рода , т. е. вероятность правильного отклонения неверной нулевой гипотезы, называют мощностью критерия. Ошибки взаимосвязаны: с уменьшением ошибки α первого рода возрастает вероятность ошибки β второго рода и наоборот. Этап 3. Определяют величину специально составленной выборочной характеристики – статистического критерия. В общем случае статистическим критерием называют однозначно определенное правило, устанавливающее условия, при 2 которых проверяемую гипотезу Н0 следует либо отвергнуть, либо принять. Основу критерия составляет специально составленная выборочная характеристика точное или приближенное распределение которой известно. Этап 4. Далее рассуждают так. Так как значения критерия позволяют судить о расхождении выборки с нулевой гипотезой, то из области допустимых значений критерия K следует выделить подобласть W таких значений, которые свидетельствовали бы о существенном расхождении данных с гипотезой Н0. Подобласть W называют критической областью. Критическая область выбирается так, чтобы вероятность попадания в нее была минимальной (равной α), если верна нулевая гипотеза Н0, и максимальной в противоположном случае. В зависимости от вида конкурирующей гипотезы и распределения критерия выбирают вид расположения критической области: правосторонняя, левосторонняя или двусторонняя. Границы (критические точки) при заданном уровне значимости находят из соотношений для критических областей: ) правосторонней: ( ; ) левосторонней: ( ; ) ) двусторонней: ( ; ( . Этап 5. В формулу критерия вместо подставляют конкретные числа, полученные в результате наблюдений, и подсчитывают числовое значение критерия. Значение критерия, вычисленное по данным выборки, называют наблюдаемым значением . Если попадает в критическую область W, то гипотеза Н0 отвергается и принимается гипотеза Н1 (на рис. 1 двусторонняя критическая область W показана желтым цветом). Если не попадет в критическую область, гипотеза Н0 не отвергается (принимается). Но это вовсе не означает, что Н0 является единственно подходящей гипотезой: просто расхождение между выборочными данными и нулевой гипотезой невелико, т. е. Н0 не противоречит результатам наблюдений. Рис. 1. Основной принцип проверки статистических гипотез Проверка гипотезы о числовом значении математического ожидания нормального распределения при известной дисперсии Пусть Х – случайная величина, имеющая нормальный закон распределения , причем числовое значение математического ожидания неизвестно, а числовое значение дисперсии известно. Дать точный ответ на вопрос, каково числовое значение неизвестного параметра, можно обследовав всю генеральную совокупность, что сделать, как правило, 3 нельзя. В этом случае проводят выборочные наблюдения и по их данным вычисляют выборочное среднее арифметическое ( ̅ ), которое дает приближенное представление о числовом значении математического ожидания. Далее действуем согласно этапам проверки статистических гипотез. Этап 1. Сформулируем нулевую и альтернативную гипотезы: и , где и - определенные предполагаемые значения параметра . Этап 2. Зададимся допустимым уровнем значимости (ошибка первого рода): . Этап 3. В качестве критерия проверки используют величину, которая зависит от выборочных данных ( ̅ ) и по значению которой можно судить о близости выборочного среднего арифметического к предполагаемому значению математиче̅ √ ского ожидания: Выбранный критерий при выполнении гипотезы подчиняется стандартному нормальному закону распределения . Этап 4. Согласно принятой альтернативной гипотезе выбираем вид критической области: при – правостороннюю; при – левостороннюю; при – двустороннюю критическую область. Границы критической области ( ) находят по таблице интегральной функции Ф(u) Лапласа (Приложение 2) из условий: в случае правосторонней критической области: ( ) – з ч ию фу ции х им з ч и гум т и и им м ; в случае левосторонней критической области: ( ) и ; при двусторонней критической области: ( ) и итич с и т чи и , г и - соответственно правая и левая критические точки. Этап 5. Подставляем в формулу критерия конкретные значения , полученные в результате наблюдений, и находим его числовое значение . Далее проверка основной гипотезы сводится к следующему: | если | , то гипотеза отвергается с вероятностью ошибки и и им тс ги т з ; | если | , то делается вывод, что основная гипотеза не противоречит опытным данным. Рассмотренные этапы проверки статистической гипотезы при известной дисперсии для удобства применения сведены в табл. 1. Пример 1. Темп роста производительности в отрасли прогнозировался на уровне 2,8%. По результатам анализа производительности 10 предприятий было установлено, что средний темп роста составил . Предполагается, что темп роста есть случайная величина, распределенная по нормальному закону с Проверить гипотезу, что темп роста производительности в отрасли вышел на прогнозируемый уровень. 1. Принимаем =2,8 и . 2. Назначаем . 3. Согласно проверяемой гипотезе в основе проверки лежит критерий: 4 ̅ √ 4. Согласно гипотезе ( ) и критическая область W – двусторонняя: и по Приложению 2 х им ; . √ 5. Т.к. нулевая гипотеза отвергается. Темп ро- ста производительности в отрасли не вышел на прогнозируемый уровень 2,8%. Таблица 1 1. Выбор гипотез , дисперсия известна и 2. Назначение 3. Критерий ̅ √ Приложение 2 4. Критическая область Левосторонняя ( 5. Критерий отклонения ) Двусторонняя ( ) ; Правосторонняя ( ) или Проверка гипотезы о числовом значении математического ожидания нормального распределения при неизвестной дисперсии Пусть Х – случайная величина, имеющая нормальный закон распределения , причем числовое значение, как математического ожидания , так и дисперсии неизвестно. В этом случае по данным наблюдений вычисляют среднее арифметическое ( ̅ ) и исправленную дисперсию . Полученные оценки дают приближенное представление о неизвестных параметрах нормального распределения (соответственно и ) и помогают сформулировать гипотезы. ̅ √ В основу проверки данной гипотезы положен критерий: который при выполнении нулевой гипотезы имеет распределение Стьюдента (t – распределение) с числом степеней свободы . Границы критической области определяют по соответствующей таблице (Приложение 6). Для односторонней критической области находят по заданному уровню значимости , помещенному в нижней строке таблицы; для двусторонней - в верхней строке. Далее проверяется принадлежность критической области W. Подробное содержание и особенности этапов проверки статистической гипотезы при неизвестной дисперсии приведены в табл. 2. Пример 2. Темп роста производительности в отрасли прогнозировался на уровне 2,6%. Предполагается, что темп роста есть случайная величина, распределенная по нормальному закону. По результатам анализа производительности 10 предприятий было установлено, что средний темп роста составил , а исправленное среднее квадратическое отклонение – 0,4%. Проверить гипотезу, что темп роста производительности в отрасли вышел на прогнозируемый уровень. 5 1. Принимаем =2,6 и 2. Назначаем . 3. Согласно проверяемой гипотезе ̅ √ им ющий с . в и Стью основе т проверки лежит критерий: t - распределение) с числом степеней свободы . 4. Согласно гипотезе критическая область W – левосторонняя: по Приложению 6 находим одностороннюю критическую точку ; . ст ст √ 5. Т.к. нулевая гипотеза не противоречит опыт- ным данным. Можно сделать вывод, что темп роста производительности в отрасли вышел на прогнозируемый уровень 2,6%. Таблица 2 1. Выбор гипотез , дисперсия неизвестна и 2. Назначение 3. Критерий ̅ – распределение √ Приложение 6 4. Критическая область Левосторонняя ст 5. Критерий отклонения Двусторонняя уст ; Правосторонняя ст или Задачи для самостоятельной работы Задача 1. Из нормальной генеральной совокупности с известным средним квадратическим отклонением извлечена выборка объема и по ней уста̅ новлено, что среднее арифметическое . Требуется проверить гипотезу о числовом значении математического ожидания: . Задача 2. По выборке объема , извлеченной из нормальной генеральной совокупности, найдены среднее арифметическое ̅ и исправленное среднее квадратическое отклонение . Требуется проверить гипотезу о числовом значении математического ожидания: . Задача 3. Настроечный размер деталей, изготовляемых станком-автоматом, составляет 35,0 мм. Контрольные измерения партии случайно отобранных обработанных деталей дали следующие результаты: хi, мм 34,8 34,9 35,0 35,1 35,3 ni 2 3 4 6 5 Требуется проверить гипотезу: обеспечивает ли станок заданный размер деталей? 6



