Специальные-главы

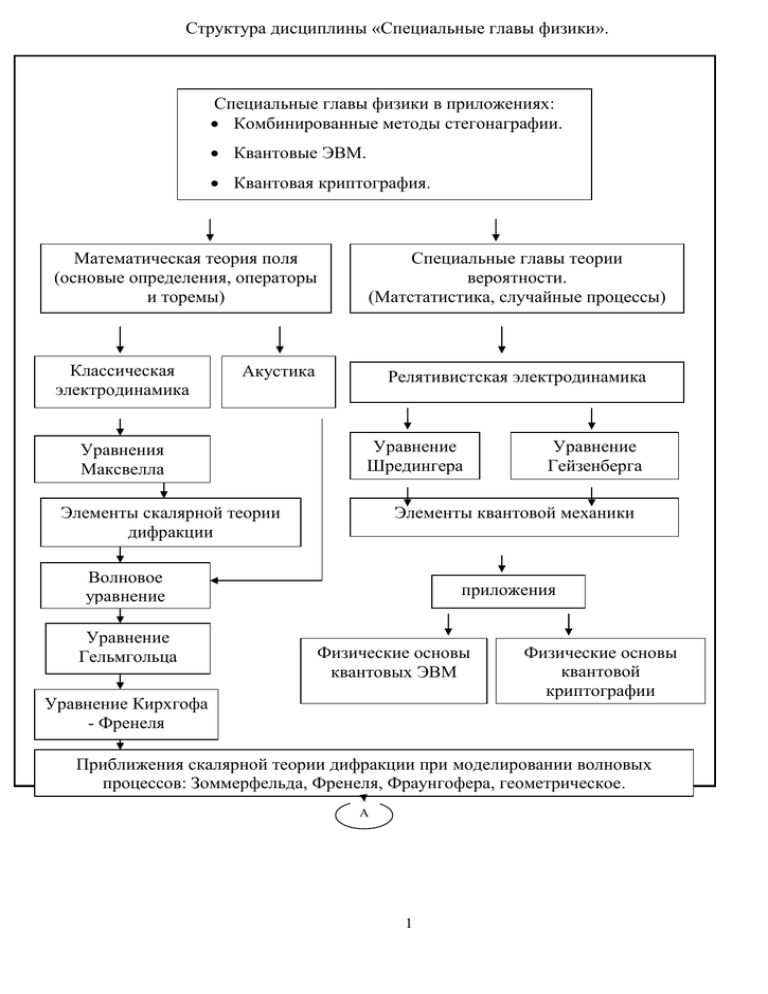
Структура дисциплины «Специальные главы физики».
Специальные главы физики в приложениях:
 Комбинированные методы стегонаграфии.
 Квантовые ЭВМ.
 Квантовая криптография.
Математическая теория поля
(основые определения, операторы
и торемы)
Специальные главы теории
вероятности.
(Матстатистика, случайные процессы)
.
Классическая
Акустика
электродинамика
chichvarin0@gmail.com
Релятивистская электродинамика
Уравнения
Максвелла
Уравнение
Шредингера
Элементы скалярной теории
дифракции
Элементы квантовой механики
Волновое
уравнение
Уравнение
Гельмгольца
Уравнение
Гейзенберга
приложения
Физические основы
квантовых ЭВМ
Уравнение Кирхгофа
- Френеля
Физические основы
квантовой
криптографии
Приближения скалярной теории дифракции при моделировании волновых
процессов: Зоммерфельда, Френеля, Фраунгофера, геометрическое.
А
1
А
Приближения при моделировании электромагнитного излучения
когерентное
некогерентное
Частично когерентное
Приложения классической
электродинамики
голография
аналоговая
цифровая
Кодирование
пространственных
сигналов
Стеганографическое
сокрытие данных на
физическом уровне
.
ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ТЕОРИИ ПОЛЯ
Градиент скалярного поля:
,
Определен, как вектор в напавлении скорейшего роста U:
Производная скалярного поля U по направлению l :
Для непрерывных функций
производными 1 порядка:
(P,
Определен поток векторного поля:
Q,
2
R)
с
непрерывными
частными
через поверхность S (поверхностный интеграл):
Дивергенция векторного поля F(P, Q, R)
div F – скаляр.
Если:
то точка M0 - источник. Соответсвеннно, точка M0 - сток, если:
Если div F = 0, векторное поле – соленоидальное. Поток соленоидального
поля через любую поверхность равен 0.
Линейный интеграл по ориентированной кривой K:
является криволинейным (работа вдоль К).
По замкнутому контуру C линейный интеграл принимает вид:
и называется циркуляцией векторного поля вдоль контура С.
Вихрь (ротор) векторного поля F(P, Q, R).
Если rot F = 0 для всех точек поля, поле безвихревое (потенциальное).
Формула Стокса.
С – замкнутый контур, ограничиваюший поверхность S c направляющими
косинусами:
3
Z
γ
S
Вектор нормали к S
β
Направление
обхода
α
X
Y
Формула Стокса в векторной форме.
Циркуляция вектора вдоль замкнутого контура С, ограничивающего
поверхность S, равна потоку вихря через эту поверхность:
Формула Остроградского – Гаусса.
Если Т – замкнутая область, ограниченная гладкой поверхностью S,
то:
Формула Остроградского – Гаусса в векторной форме.
- интеграл от дивергенции векторного поля F, распространенный по обьему Т
равен потоку вектора через поверхность S, ограничивающую объем Т.
Формула Грина.
С – граница области D. P(X, Y), Q(X, Y) – непрерывны в замкнутой области
D,
𝜕𝑄
𝜕𝑃
и непрерывны в 𝑫. Тогда:
𝜕𝑥
𝜕𝑦
4
Основы теории Максвелла для электромагнитного поля
1. Вихревое электрическое поле
Из
закона
Фарадея
ξ=dФ/dt
следует, что любое изменение сцепленного с контуром потока магнитной индукции
приводит к возникновению электродвижущей силы индукции и вследствие этого
появляется индукционный ток. Следовательно, возникновение э.д.с. электромагнитной индукции возможно и в неподвижном контуре, находящемся в переменном магнитном поле. Однако э.д.с. в любой цепи возникает только тогда, когда в ней
на носители тока действуют сторонние силы — силы неэлектростатического происхождения. Поэтому возникает вопрос о природе сторонних сил в данном случае.
Опыт показывает, что эти сторонние силы не связаны ни с тепловыми, ни с химическими процессами в контуре; их возникновение также нельзя объяснить силами
Лоренца, так как они на неподвижные заряды не действуют. Максвелл высказал
гипотезу, что всякое переменное магнитное поле возбуждает в окружающем пространстве электрическое поле, которое и является причиной возникновения индукционного тока в контуре. Согласно представлениям Максвелла, контур, в котором появляется э.д.с., играет второстепенную роль, являясь своего рода лишь
«прибором», обнаруживающим это поле.
Итак, по Максвеллу, изменяющееся во времени магнитное поле порождает электрическое поле ЕB, циркуляция которого,
1
1
где EBl — проекция вектора EB на направление dl.
Подставив в формулу (1) выражение
получим
Если поверхность и контур неподвижны, то операции дифференцирования и интегрирования можно поменять местами. Следовательно,
5
2.
где символ частной производной подчеркивает тот факт, что интеграл
является
функцией только от времени.
Циркуляция вектора напряженности электростатического поля (обозначим его
EQ)
вдоль любого замкнутого контура равна нулю:
0
3.
Сравнивая выражения (1) и (3), видим, что между рассматриваемыми полями (ЕB и
EQ)
имеется принципиальное различие: циркуляция вектора ЕB в отличие от
циркуляции вектора
EQ
не равна нулю. Следовательно, электрическое поле ЕB,
возбуждаемое магнитным полем, как и само магнитное поле, является вихревым.
2. Ток смещения
Согласно Максвеллу, если всякое переменное магнитное поле возбуждает в окружающем пространстве вихревое электрическое поле, то должно существовать и обратное явление: всякое изменение электрического поля должно вызывать появление
в окружающем пространстве вихревого магнитного поля. Для установления
количественных соотношений между изменяющимся электрическим полем и
вызываемым им магнитным полем Максвелл ввел в рассмотрение так называемый
ток смещения.
Рассмотрим цепь переменного тока, содержащую конденсатор (рис. 196). Между
обкладками заряжающегося и разряжающегося конденсатора имеется переменное
электрическое поле, поэтому, согласно Максвеллу, через конденсатор
«протекают» токи смещения, причем в тех участках, где отсутствуют проводники.
Найдем количественную связь между изменяющимся электрическим и вызываемым
им магнитным полями. По Максвеллу, переменное электрическое поле в конденсаторе в каждый момент времени создает такое магнитное поле, как если бы
6
между обкладками конденсатора существовал ток проводимости, равный току в
подводящих проводах. Тогда можно утверждать, что токи проводимости (I) и смещения (Iсм) равны: Iсм=I. Ток проводимости вблизи обкладок конденсатора
2.1
(поверхностная плотность заряда  на обкладках равна электрическому смещению D
в конденсаторе. Подынтегральное выражение в (2.1) можно рассматривать как
частный случай скалярного произведения (дD/дt)dS, когда дD/дt и dS взаимно
параллельны. Поэтому для общего случая можно записать
Сравнивая это выражение с I=Iсм =
, имеем
2.2
Выражение (2.2) и было названо Максвеллом плотностью тока смещения.
Рассмотрим, каково же направление векторов плотностей токов проводимости и
смещения j и jсм. При зарядке конденсатора (рис. 197, а) через проводник, соединяющий обкладки, ток течет от правой обкладки к левой; поле в конденсаторе
усиливается, вектор D растет со временем;
следовательно, дD/дt>0, т.е. вектор дD/дt
7
направлен в ту же сторону, что и D. Из рисунка видно, что направления векторов
дD/дt и j совпадают. При разрядке конденсатора (рис. 197, б) через проводник, соединяющий обкладки, ток течет от левой обкладки к правой; поле в конденсаторе
ослабляется, вектор D убывает со временем; следовательно, дD/дt<0, т. е. вектор at
дD/дt направлен противоположно вектору D. Однако вектор дD/дt направлен опять
также, как и вектор j. Из разобранных примеров следует, что направление вектора j,
а следовательно, и вектора jсм совпадает с
направлением
вектора
дD/дt,как это и следует из формулы (2.2).
Подчеркнем, что из всех физических свойств, присущих току проводимости,
Максвелл приписал току смещения лишь одно — способность создавать в окружающем пространстве магнитное поле. Таким образом, ток смещения (в вакууме или
веществе) создает в окружающем пространстве магнитное поле (линии индукции
магнитных полей токов смещения при зарядке и разрядке конденсатора показаны на
рис. 197 штриховой линией).
В диэлектриках ток смещения состоит из двух слагаемых. Так D=0E+P, где Е —
напряженность электростатического поля, а Р — поляризованность, то плотность
тока смещения
2.3
где 0дE/дt — плотность тока
смещения в вакууме, дP/дt — плотность тока
поляризации — тока, обусловленного упорядоченным движением электрических
зарядов в диэлектрике (смещение зарядов в неполярных молекулах или поворот
диполей в полярных молекулах). Возбуждение магнитного поля токами поляризации
правомерно, так как токи поляризации по своей природе не отличаются от токов
проводимости.
Однако то, что и другая часть плотности тока смещения (0дE/дt), не связанная с
движением зарядов, а обусловленная только изменением электрического поля во
времени, также возбуждает магнитное поле, является принципиально новым
утверждением Максвелла. Даже в вакууме всякое изменение во времени
электрического поля приводит к возникновению в окружающем пространстве магнитного поля.
Следует отметить, что название «ток смещения» является условным, а точнее —
исторически сложившимся, так как ток8 смещения по своей сути — это изменяющееся со временем электрическое поле. Ток смещения поэтому существует не
только в вакууме или диэлектриках, но и внутри проводников, по которым течет
переменный ток. Однако в данном случае он пренебрежимо мал по сравнению с током проводимости. Наличие токов смещения подтверждено экспериментально советским физиком А. А. Эйхенвальдом, изучавшим магнитное поле тока поляризации,
который, как следует из (3.3), является частью тока смещения.
Максвелл ввел понятие полного тока, равного сумме токов проводимости (а также
конвекционных токов) и смещения. Плотность полного тока:
jполн=j+дD/дt.
Введя понятия тока смещения и полного тока, Максвелл по-новому подошел к рассмотрению замкнутости цепей переменного тока. Полный ток в них всегда замкнут,
т. е. на концах проводника обрывается лишь ток проводимости, а в диэлектрике
(вакууме) между концами проводника имеется ток смещения, который замыкает ток
проводимости.
Максвелл обобщил теорему о циркуляции вектора Н, введя в ее правую часть
полный ток Iполн=
сквозь поверхность S, натянутую на замкнутый контур
L. Тогда обобщенная теорема о циркуляции вектора Н запишется в виде
2.4
Выражение (2.4) справедливо всегда, свидетельством чего является полное соответствие теории и опыта.
3. Уравнения Максвелла для электромагнитного поля
Введение Максвеллом понятия тока смещения привело его к завершению созданной
им единой макроскопической теории электромагнитного поля, позволившей с
единой точки зрения не только объяснить электрические и магнитные явления, но и
предсказать новые, существование которых было впоследствии подтверждено.
В основе теории Максвелла лежат рассмотренные выше четыре уравнения:
1) Электрическое поле может быть как потенциальным (EQ), так и вихревым (ЕB),
поэтому напряженность суммарного поля Е=ЕQ+ЕB. Так как циркуляция вектора
EQ
равна нулю, а циркуляция вектора ЕB определяется выражением (2.2), то циркуляция
вектора напряженности суммарного поля
9
Это уравнение показывает, что источниками электрического поля могут быть не
только электрические заряды, но и меняющиеся во времени магнитные поля.
2) Обобщенная теорема о циркуляции вектора Н (см. (2.4)):
Это уравнение показывает, что магнитные поля могут возбуждаться либо движущимися зарядами (электрическими токами), либо переменными электрическими
полями.
3. Теорема
Гаусса
для
поля
D:
3.1
Если заряд распределен внутри замкнутой поверхности непрерывно с объемной
плотностью , то формула (3.1) запишется в виде
4. Теорема
Гаусса
для
поля
В:
Итак, полная система уравнений Максвелла в интегральной форме:
Величины, входящие в уравнения Максвелла, не являются независимыми и между
ними существует следующая связь (изотропные не сегнетоэлектрические и не
ферромагнитные среды):
D=0E,
В=0Н,
j=E, закон Ома.
где 0 и 0 — соответственно электрическая и магнитная постоянные,  и  —
10
соответственно диэлектрическая и магнитная
проницаемости,  — удельная прово-
димость
вещества.Из
уравнений
Максвелла
вытекает,
что
источниками
электрического поля могут быть либо электрические заряды, либо изменяющиеся во
времени магнитные поля, а магнитные поля могут возбуждаться либо движущимися
электрическими
зарядами
(электрическими
токами),
либо
переменными
электрическими полями. Уравнения Максвелла не симметричны относительно
электрического и магнитного полей. Это связано с тем, что в природе существуют
электрические заряды, но нет зарядов магнитных.
Для стационарных полей (Е=const и В=const) уравнения Максвелла примут вид
т. е. источниками электрического поля в данном случае являются только электрические заряды, источниками магнитного — только токи проводимости. В данном
случае электрические и магнитные поля независимы друг от друга, что и позволяет
изучать отдельно постоянные электрическое и магнитное поля.
Воспользовавшись известными из векторного анализа теоремами Стокса и Гаусса
можно представить полную систему уравнений Максвелла в дифференциальной
форме (характеризующих поле в каждой точке пространства):
Если заряды и токи распределены в пространстве непрерывно, то обе формы
уравнений Максвелла — интегральная и дифференциальная — эквивалентны.
Однако когда имеются поверхности разрыва — поверхности, на которых свойства
среды или полей меняются скачкообразно, то интегральная форма уравнений является более общей.
Уравнения Максвелла в дифференциальной форме предполагают, что все величины
11
в пространстве и времени изменяются непрерывно.
Чтобы достичь математической
эквивалентности обеих форм уравнений Максвелла, дифференциальную форму
дополняют граничными условиями, которым должно удовлетворять электро-
магнитное поле на границе раздела двух сред. Интегральная форма уравнений
Максвелла содержит эти условия.
D1n=D2n, E1=E2, B1n=B2n, H1= H2
(первое и последнее уравнения отвечают случаям, когда на границе раздела нет ни
свободных зарядов, ни токов проводимости).
Уравнения Максвелла — наиболее общие уравнения для электрических и магнитных
полей в покоящихся средах. Они играют в учении об электромагнетизме такую же
роль, как законы Ньютона в механике. Из уравнений Максвелла следует, что
переменное магнитное поле всегда связано с порождаемым им электрическим полем,
а переменное электрическое поле всегда связано с порождаемым им магнитным, т. е.
электрическое и магнитное поля неразрывно связаны друг с другом — они образуют
единое электромагнитное поле.
Теория Максвелла, являясь обобщением основных законов электрических и магнитных явлений, смогла объяснить не только уже известные экспериментальные
факты, что также является важным ее следствием, но и предсказала новые явления.
Одним из важных выводов этой теории явилось существование магнитного поля
токов
смещения,
электромагнитных
что
позволило
волн
—
Максвеллу
предсказать
переменного
существование
электромагнитного
поля,
распространяющегося в пространстве с конечной скоростью. В дальнейшем было
доказано,что скорость распространения свободного электромагнитного поля (не
связанного с зарядами и токами) в вакууме равна скорости света с = 3•108 м/с. Этот
вывод и теоретическое исследование свойств электромагнитных волн привели
Максвелла к созданию электромагнитной теории света, согласно которой свет
представляет собой также электромагнитные волны. Электромагнитные волны на
опыте были получены немецким физиком Г. Герцем (1857—1894), доказавшим, что
законы их возбуждения и распространения полностью описываются уравнениями
Максвелла.
Таким
образом,
теория
Максвелла
была
экспериментально
подтверждена.
К электромагнитному полю применим только принцип относительности Эйнштейна,
так как факт распространения электромагнитных волн в вакууме во всех системах
отсчета с одинаковой скоростью с не совместим с принципом относительности
Галилея.
Согласно принципу относительности12Эйнштейна, механические, оптические и
электромагнитные явления во всех инерциальных системах отсчета протекают
одинаково, т. е. описываются одинаковыми уравнениями. Уравнения Максвелла
инвариантны относительно преобразований Лоренца: их вид не меняется при
переходе
от одной инерциальной системы отсчета к другой, хотя величины Е, В, D, Н в них
преобразуются по определенным правилам.
Из принципа относительности вытекает, что отдельное рассмотрение электрического
и магнитного полей имеет относительный смысл. Так, если электрическое поле
создается системой неподвижных зарядов, то эти заряды, являясь неподвижными
относительно одной инерциальной системы отсчета, движутся относительно другой
и, следовательно, будут порождать не только электрическое, но и магнитное поле.
Аналогично, неподвижный относительно одной инерциальной системы отсчета
проводник с постоянным током, возбуждая в каждой точке пространства постоянное
магнитное поле, движется относительно других инерциальных систем, и создаваемое
им переменное магнитное поле возбуждает вихревое электрическое поле.
Таким образом, теория Максвелла, ее экспериментальное подтверждение, а также
принцип относительности Эйнштейна приводят к единой теории электрических,
магнитных и оптических явлений, базирующейся на представлении об электромагнитном поле.
Слайд 1
Волновая теория
13
Слайд 2
Связь магнитного и электрического поля
• Электрический ток создаёт магнитную индукцию
(закон Ампера)B = μ I/2πr
• Переменный поток магнитного поля создаёт
электрическое поле (закон Фарадея)I = dф/dt
14
Слайд 3
Второе уравнение Максвелла
•
•
•
В основной статье Максвелл впервые сформулировал понятие
электромагнитного поля как физической реальности, имеющей собственную
энергию и конечное время распространения, определяющее запаздывающий
характер электромагнитного взаимодействия.
Не только ток, но и изменяющееся со временем электрическое поле (ток
смещения) порождает магнитное поле. В свою очередь, в силу закон
Фарадея, изменяющееся магнитное поле снова порождает электрическое.
Второе уравнение Максвелла выражает закон электромагнитной индукции
Фарадея: ЭДС в любом замкнутом контуре равна скорости изменения (т. е.
производной по времени) магнитного потока.
Итак, получаем: rotE = - dB/dt.
В результате, в пустом пространстве может распространяться электромагнитная волна.
Из уравнений Максвелла следовало, что её скорость равна скорости свет,
поэтому Максвелл сделал вывод об электромагнитной природе света.
15
Слайд 4
Третье и четвертое уравнения
Максвелла
•
Они основаны на теореме Гаусса, утверждающей, что поток вектора электрической
индукции через любую замкнутую поверхность равен заряду внутри этой поверхности.
•
Третье уравнение Максвелла: div D = р.
•
Четвертое уравнение утверждает, что магнитных зарядов в природе не существует,
поэтому:div B = 0.
Распространение электромагнитных волн со скоростю света первоначально
интерпретировалось как возмущения некоторой среды, так называемого эфира.
Классическая электродинамика, основанная на уравнениях Максвелла, лежит в основе
многочисленных приложений электро- и радиотехники, СВЧ и оптики. До настоящего
времени не было обнаружено ни одного эффекта, который потребовал бы
видоизменения уравнений.
16
Слайд 5
Дифференциальная форма уравнений
Максвелла
•
Уравнения Максвелла представляют собой систему из восьми (два
векторных с тремя компонентами каждое и два скалярных)
линейных дифференциальных уравнений в частных производных
1-го порядка для 12 компонент четырёх векторных функций ( D,E,H,B):
17
Слайд 6
Интегральная форма уравнений
Максвелла
18
Слайд 7
Уравнения Максвелла в среде
•
Чтобы получить полную систему уравнений электродинамикик системе уравнений
Максвелла необходимо добавить материальные уравнения, связывающие
величины j, H , D , E , B, в которых учтены индивидуальные свойства среды. Способ
получения материальных уравнений дают молекулярные
теории поляризации, намаг и электропроводиченностиности среды, использующие
идеализированные модели среды. Применяя к ним уравнения
классической или квантовой механики, а также методы статистической физики, можно
установить связь между векторами j, H , D с одной стороны и E, B с другой стороны.
Связанные заряды и токи
19
Слайд 8
Материальные уравнения
•
Материальные уравнения устанавливают связь между D, H и E, B . При этом
учитываются индивидуальные свойства среды. На практике в материальных уравнениях
обычно используются экспериментально определяемые коэффициенты (зависящие в
общем случае от частоты электромагнитного поля), которые собраны в различных
справочниках физических величин.
В слабых электромагнитных полях, сравнительно медленно меняющихся в
пространстве и во времени, в случае изотропных, неферромагнитных и не
сегнетоэлектрических сред справедливо приближение, в котором
поляризуемость и намагниченность линейно зависят от приложенных полей:
20
Слайд 9
Продолжение…
В проводниках существует связь между плотностью тока и напряжённостью
электрического поля, выражаемая законом Ома:
В анизотропной среде связь между напряжённостями полей и индукциями имеют
различные коэффициенты по каждой координате.
21
Слайд 10
Продолжение…
Хотя для широкого класса веществ линейное приближение для слабых полей
выполняется с хорошей точностью, в общем случае зависимость между
D, H и E, B может быть нелинейной. В этом случае проницаемости среды не
являются константами, а зависят от величины поля в данной точке. Кроме того, более
сложная связь между D, H и E, B наблюдается в средах с пространственной или
временной дисперсиями. В случае пространственной дисперсии токи и заряды в
данной точке пространства зависят от величины поля не только в той же точке, но и в
соседних точках. В случае временной дисперсии поляризация и намагниченность
среды не определяются только величиной поля в данный момент времени, а зависят
также от величины полей в предшествующие моменты времени. В самом общем
случае нелинейных и неоднородных сред с дисперсией, материальные уравнения в
системе СИ принимают интегральный вид:
22
Слайд 11
Уравнения в изотропных и однородных
средах без дисперсии
• В изотропных и однородных средах без дисперсии уравнения
Максвелла принимают следующий вид:
23
Слайд 12
Граничные условия
•
Во многих случаях неоднородную среду можно представить в виде совокупности
кусочно-непрерывных однородных областей, разделённых бесконечно тонкими
границами. При этом можно решать уравнения Максвелла в каждой области, «сшивая»
на границах получающиеся решения. В частности, при рассмотрении решения в
конечном объёме необходимо учитывать условия на границах объёма с окружающим
бесконечным пространством. Граничные условия получаются из уравнений Максвелла
предельным переходом. Для этого проще всего воспользоваться уравнениями
Максвелла в интегральной форме.
Выбирая во второй паре уравнений контур интегрирования в виде прямоугольной
рамки бесконечно малой высоты, пересекающей границу раздела двух сред, можно
получить следующую связь между компонентами поля в двух областях, примыкающих к
границе:
24
Слайд 13
Продолжение…
Эти граничные условия показывают непрерывность нормальной компоненты
вектора магнитной индукции (нормальная компонента электрической индукции
непрерывна только при отсутствии на границе поверхностных зарядов).
25
Слайд 14
Волновое уравнение
•
Уравнения Максвелла являются дифференциальными уравнениями первого
порядка по координатам и времени. Однако, во второй паре в каждое
уравнение входят обе неизвестные векторные функции E и B. При отсутствии
зарядов и токов можно перейти к уравнениям второго порядка, каждое из
которых зависит только от одного, электрического или магнитного поля:
Такие уравнения называются волновыми.
26
Слайд 15
Уравнение Гельмгольца
•
При отсутствии электрических зарядов в среде, уравнение
Гельмгольца принимает вид:
где
27
Слайд 16
Плоские электромагнитные волны
•
Предположим, что напряжённость электрического поля и магнитная
индукция являются произвольными функциями следующей комбинации
координат и времени:
где n — некоторый постоянный вектор. В этом случае E и B удовлетворяют
уравнениям Максвелла в отсутствие зарядов и токов, если между ними существует
следующая связь:
28
Слайд 17
Вывод решения для плоской волны
29
Слайд 18
Продолжение…
• Вектор Пойнтинга (плотность потока энергии), независимо от системы
единиц, связан с полной плотностью энергии следующим образом:
Это соотношение соответствует уравнению связи импульса и энергии для
безмассовой частицы в релятивистской теории. Однако, скорость
в среде меньше чем скорость света в вакууме .
30
Слайд 19
Продолжение…
•
Важный частный случай решения в виде плоских волн возникает, когда напряжённости
полей являются гармоническими периодическими функциями. Выберем координатную
ось Z вдоль волнового вектора k. Тогда вектор электрического поля (как, впрочем, и
магнитного) будет лежать в плоскости
то есть
. Если по каждой проекции в этой плоскости электрическое поле
совершает периодические колебания, то такую волну называют монохроматической
плоской волной:
Сравнение с общим решением для плоской волны, приводит к следующей связи между
вектором k и константой , которое называется уравнением дисперсии:
В этом случае, вектор k называется волновым вектором, а — круговой
частотой монохроматической электромагнитной волны. Модуль волнового вектора и
круговая частота связаны с длиной волны и её частотой следующим образом:
31
Слайд 20
Численное решение уравнений Максвелла
•
•
Основными методами являются проекционные, в которых решение проецируется на
какой-либо удобный функциональный базис, и дискретизационные — область
пространства разбивается на множество малых конечных областей.
Для компьютерных расчетов чаще применяются более универсальные
дискретизационные методы:
Метод конечных элементов (FEM), который используется для решения широкого
класса задач, сводящихся к уравнениям в частных производных. В методе конечных
элементов рассматриваемая область пространства, в которой ищется решение,
разбивается на большое число простых дискретных элементов, обычно, но не
обязательно, треугольной (в двумерном случае) или тетраэдральной формы (в
трёхмерном случае). Форма и плотность элементов адаптируются к требованиям
задачи. Поведение отдельных элементов рассматривается как результат линейного
взаимодействия соседних узлов решётки разбиения под действием внешних сил и
описывается матричными уравнениями. Решение задачи сводится, таким образом, к
решению разреженных систем большого числа линейных матричных уравнений.
Метод конечных разностей во временной области (FDTD) для нахождения временных
и спектральных зависимостей был разработан специально для решения уравнений
Максвелла, в которых изменение электрического и магнитного поля во времени
зависит от изменения, соответственно, магнитного и электрического поля в
пространстве. В рамках этого метода область пространства и временной интервал
подвергаются равномерной дискретизации с заданием начальных условий.
Полученные из уравнений Максвелла конечно-разностные уравнения решаются в
каждый последующий момент временной сетки, пока не будет получено решение
поставленной задачи на всем требуемом временном интервале.
32
Слайд 21
Продолжение…
•
•
•
•
•
Идея метода конечных разностей (метода сеток) известна давно, с
соответствующих трудов Эйлера. Однако практическое применение этого
метода было тогда весьма ограничено из-за огромного объема ручных
вычислений, связанных с размерностью получаемых систем алгебраических
уравнений, на решение которых требовались годы. В настоящее время, с
появлением быстродействующих компьютеров, ситуация в корне изменилась.
Этот метод стал удобен для практического использования и является одним
из наиболее эффективных при решении различных задач математической
физики.
Основная идея метода конечных разностей (метода сеток) для
приближенного численного решения краевой задачи для двумерного
дифференциального уравнения в частных производных состоит в том, что
1) на плоскости в области А, в которой ищется решение, строится сеточная
область Аs (рис.1), состоящая из одинаковых ячеек размером s ( s – шаг
сетки) и являющаяся приближением данной области А;
2) заданное дифференциальное уравнение в частных производных
заменяется в узлах сетки Аs соответствующим конечно-разностным
уравнением;
3) с учетом граничных условий устанавливаются значения искомого решения
в граничных узлах области Аs .
33
Слайд 22
Продолжение…
Решая полученную систему конечно-разностных алгебраических уравнений,
получим значения искомой функции в узлах сетки Аs , т.е. приближенное
численное решение краевой задачи. Выбор сеточной области Аs зависит от
конкретной задачи, но всегда надо стремиться к тому, чтобы контур сеточной
области Аs наилучшим образом аппроксимировал контур области А.
Рассмотрим простейший и наглядный случай (уравнение Лапласа)
(1)
Где p ( x, y ) – искомая функция, x, y –
прямоугольные координаты плоской области и получим
соответствующее ему конечно-разностное уравнение.
34
Слайд 23
Продолжение…
Заменим частные производные
разностными отношениями:
и
в уравнении (1) конечно-
Тогда решая уравнение (1) относительно p ( x, y ), получим:
(2)
• Задав значения функции p ( x, y ) в граничных узлах контура сеточной
области Аs в соответствии с граничными условиями и решая
полученную систему уравнений (2) для каждого узла сетки, получим
численное решение нашей краевой задачи (1) в заданной областиА.
• Число уравнений вида (2) равно количеству узлов сеточной
области Аs, и чем больше узлов, т.е. чем мельче сетка, тем меньше
погрешность вычислений. Однако с уменьшением шага s возрастает
размерность системы уравнений и следовательно, время решения.
Волновое уравнение электродинамики в приближении скалярной теории
В рамках скалярной теории дифракции в любой точке
однородной
среды в областях, свободных от токов и зарядов (в частности, отсутствуют
источники излучения), вещественная функция
, которая описывает
электромагнитное возмущение, удовлетворяет скалярному однородному
волновому уравнению
где
– оператор Лапласа;
– скорость света в среде;
км/с – скорость света в вакууме;
– показатель преломления.
В скалярной теории дифракции
представляет собой одну из двух
взаимно перпендикулярных декартовых компонент
и
электрического поля, колеблющихся в плоскости, перпендикулярной
направлению распространения волны. Скалярная теория не позволяет учесть
явление поляризации и тонкие эффекты дифракции. Однако для инженерных
приложений, в частности при модельном представлении реальных КПС такое
допущение дает удовлетворительные результаты. Но даже при описанных
допущениях решить волновое уравнение удается для небольшого числа
частных случаев. Одним из таких решений является модель, которая строится
на представлении суперпозиции плоских и сферических волн. Такая модель с
достаточной адекватностью позволяет описывать
преобразование сигналов в
35
ультрафиолетовом, оптическом и инфракрасном диапазонах. В некоторых
диапазонах электромагнитного излучения, используемых радиоэлектронными
системами (РЭС), входящими в состав КПС, ограничения скалярной теории
дифракции недопустимы. Границы ее применимости рассматриваются на
основе соответствующих классификаций.
РЭС могут работать в диапазоне от 3 кГц до 300 ГГц. Несущая частота
сигнала, передающего (несущего) сообщение, существенно влияет на
распространение, отражение и рассеяние радиоволн. Поэтому весь
радиодиапазон частот условно разделен на участки, каждый из которых имеет
свои особенности, в частности способ модельного представления (табл. 1).
Таблица 1
Диапазон
радиочастот
Длина
волны
Название
диапазона
радиочастот
Название
диапазона
радиоволн
3...30 кГц
10...100
км
Сверхнизкие
частоты (СНЧ)
Мириаметровые
волны
30...300 кГц
1...10 км
Низкие частоты
Километровые
волны
0.3...3 МГц
100...1000
м
Средние частоты
Гектометровые
волны
3...30 МГц
10...100 м
Высокие частоты
Декаметровые
волны
30...300 МГц
1...10 м
Очень высокие
частоты (ОВЧ)
Метровые волны
300...3000
МГц
0,1...1 м
Ультравысокие
частоты (УВЧ)
Дециметровые
волны
3...30 ГГц
1...10 см
Сверхвысокие
частоты (СВЧ)
Сантиметровые
волны
30...300 ГГц
0,1...10 см
Крайне высокие
частоты (КВЧ)
Миллиметровые
волны
Дециметровые волны распространяются только в пределах прямой видимости,
интенсивно отражаются от объектов, благодаря наличию совершенной
элементной базы в соответствующих РЭС достигается направленность
излучения и приема.
Сантиметровые волны также распространяются только в пределах прямой
видимости, интенсивно отражаются от различных объектов, что позволяет
организовывать защищенные КПС даже в условиях возникновения
ретроотражений в замкнутых пространствах. Возможно достижение высокой
направленности излучения и приема. Элементная база позволяет реализовать
КПС с псевдослучайным сканированием несущей и псевдослучайным
распределением поднесущих частот.
Миллиметровые волны поглощаются в атмосфере в самой высокой
степени.направленности. РЭС, реализующие соответствующие КПС, обладают
высокой направленностью излучения и приема.
Как показывает анализ, наиболее часто в РЭС применяются диапазоны ОВЧ,
36
УВЧ и СВЧ. Излучение в этих диапазонах частот интенсивно отражаются от
объектов, антенны компактны и обеспечивают высокую направленность
излучения и приема. Анализ РЭС связи показывает перспективность
применения этих диапазонов. Для этих диапазонов наиболее активно
развивается элементная база РЭС. Если в КПС с РЭС не используется эффект
поляризации и выполняются описанные ниже условия рассматриваемая
модель приемлема.
Рис.1. Зоны свободного пространства,
Зоммерфельда, Френеля и Фраунгофера
где
наблюдается
дифракция
Рис.2. Зоны пространства за фокусирующим элементом (объектив ОС, антенна
РЛС), где наблюдается дифракция Френеля и Фраунгофера
1.1. Скалярные монохроматические волны
В волновой теории элементарным сигналом считают монохроматическую
волну, распространяющуюся в пространстве и во времени. Если ее временная
частота
лежит приблизительно в интервале от
до
Гц
(соответственно длина волны в вакууме изменяется от 0,75 мкмдо 0,4 мкм),
то речь идет об оптическом диапазоне. Если длина волны в вакууме
изменяется от 0,75 мкм до 30 мкм, то такой диапазон называется
инфракрасным. Для радиодиапазона длина волны изменяется от долей мм до
десятков километров. Решение волнового уравнения (1), определяющее вид
монохроматической волны в точке
в момент времени , можно
представить в виде скалярной функции
Величину
косинуса
времени
,
большую
нуля,
– полной
называют амплитудой,
фазой,
зависящей
а
аргумент
как
от
так и от пространственных координат
.
Величину
называют временной,
илициклической,
частотой оптического излучения (представляет число колебаний в секунду,
Гц), которая по порядку величины равна
Гц, а величину
–
угловой частотой. Последняя определяет число колебаний в
секунд. При
замене на
значение функции 37 остается неизменным, поэтому
является временным периодом колебаний. Волновую функцию в форме (4)
называют временным гармоническим оптическим сигналом. Она определяет
монохроматическую волну. В случае линейно поляризованной волны
характеризует напряженность электрического или магнитного поля как
физическую величину.
Расчеты, связанные с преобразованием гармонических сигналов, значительно
упрощаются, если вместо косинусоидальной гармоники использовать
комплексную экспоненциальную гармонику. Нетрудно заметить, что
можно записать в виде действительной части
от комплексной
гармонической функции координат и времени
где
- комплексный пространственно-временной гармонический сигнал.
Комплексную функцию координат
называют комплексной амплитудой волны, или комплексным оптическим
сигналом.
Так как зависимость от времени
известна заранее, то задание
комплексной
амплитуды
достаточно
для
описания
светового
возмущения.
Поверхность постоянной фазы, в любой точке
которой в данный момент
времени фаза волны одинакова,
называютволновым фронтом.
Вообще говоря, поверхность постоянной фазы в
не совпадает с
поверхностью постоянной амплитуды. При этом говорят, что такая
волна неоднородна. Примером неоднородных волн служат эрмито-гауссовые
и лагерро-гауссовые волны на выходе лазера.
Если операции, производимые над
, линейны, то для удобства
математических выкладок символ
в
опускается, а в
вещественная
функция
заменяется комплекснозначной
. Тогда вещественная
часть окончательного выражения будет представлять собой изучаемую
физическую величину. Делая переход к комплексным оптическим сигналам,
следует
помнить,
что
фактически
физическая
величина
напряженности
вещественн
электрического поля в электромагнитной волне всегда
Волновое уравнение акустики
Рассмотрим основные соотношения, характеризующие упругую среду.
Пусть в некоторый начальный момент объем упругой среды увеличился и
занял объем V. Тогда относительное изменение V,  , называемое
расширением, определится как:
V
  (V  V0 ) V0 
.
V0
При изменении объема меняется плотность среды  . Относительное
изменение плотности S, называемое уплотнением, определяется как:
(    0 ) 
S

0
0
Основываясь на очевидном равенстве
V   0V0 ,
получим:
38
1  S    S  1.
При условии S  1;   1 , что обычно достаточно хорошо соблюдается в
акустике, получим:
S   .
При малых изменениях объема относительное изменение плотности равно
относительному изменению объема с обратным знаком.
Относительное изменение объема в упругой среде сопровождается
изменением давления P  P  P0 . P - обозначается как p и носит название
избыточного или звукового давления. Очевидно, что P пропорционально
расширению
P  P     S ,
где  - коэффициент объемной упругости, C  1
- коэффициент

сжимаемости.
Вывод волнового уравнения акустики. Соотношение между давлением и
линейной деформацией.
Выделим элементарный объем образованный ограниченными одинаковыми
участками плоскостей, перпендикулярными оси Х.
При малых смещениях

  x ,
x

где
- линейная деформация, можно положить, что
x
V d

,
V0 dx
тогда

p  
,
x
т.е. звуковое давление пропорционально линейной деформации.
Если на грани а1b1 существует давление р, то на грани а2b2 в этот же момент
оно равно p  p ;
Давление р есть функция координат х, следовательно
p
p  x
x
Составим уравнение движения выделенного
объема. Масса объема равна x ,
39
 2
ускорение 2 , результирующая сила равна p , получим уравнение:
t
 2
x 2  p ,
t
с учетом p получим:

 2
t
2

p
x
и используя выражение p   
 2
t 2
 c
 2
x 2
где c  
p

, получим:
x
,

1
c
.
Уравнение называется волновым уравнением и является основным,
описывающим распространение звуковых волн.
Величина c называется удельным акустическим или волновым
сопротивлением и является важной акустической характеристикой среды.
Решения волнового уравнения электродинамики.
Начнем с самого простого случая – пространственно одномерного волнового
уравнения
.
(8)
V - скорость света в среде, отличной от вакуума, где V = C
Общее решение этого уравнения ищем в виде
,
(9)
где
и
– произвольные функции, а аргументы этих функций
представляют собой специальные комбинации переменных
и
постоянной .
Если в момент
графически изобразить функции
и
, то в
последующие моменты времени эти функции смещаются вдоль оси
со
скоростью
как
целое:
– вправо, а
– влево.
Ограничимся для простоты гармоническими монохроматическими волнами, т.
е. синусоидальными волнами с одной циклической частотой:
.
Гармоническая зависимость любой величины от времени может быть
представлена в общем виде так:
,
(поскольку формула Эйлера утверждает, что для любого вещественного
числа выполнено следующее равенство:
40
,)
– значение рассматриваемой величины возмущения в точке с
координатой в начальный момент времени:
.
Решение волнового уравнения (8), удовлетворяющее условию (9) и дающее
гармоническую зависимость от , в комплексной форме имеет вид
.
(10)
Фаза волны, т. е. ее состояние в данной точке пространства в данный момент
времени, определяется выражением
. В данный момент времени
поверхность равной фазы – волновой фронт – описывается
уравнением:
. Это плоскость, нормальная к оси . Поверхность
равной фазы (волновой фронт) распространяется вправо с фазовой
скоростью . (вернемся к численному рашению уравнений Максвелла на
демонстрации
решения
методом
FTDT)
Поскольку волновой фронт в данном случае является плоскостью, мы
получили плоскую волну. Нам понадобится еще выражение для плоской
волны,
распространяющейся
в
произвольном
направлении,
характеризуемом постоянным
единичным
вектором
.
Поскольку
уравнение плоскости, перпендикулярной вектору
, имеет вид
, плоскую волну можно записать в виде
.
(11)
Введем волновой вектор , определив его как
,
где
– единичный вектор в направлении распространения волны (в
направлении ). Тогда плоская волна может быть представлена в
комплексной форме:
(12)
.
(13)
Вектор
называют волновым вектором потому, что он имеет
непосредственное отношение к длине волны и всегда перпендикулярен фронту
волны.
Длиной волны здесь называется расстояние (отсчитанное в направлении
движения волны) между двумя ближайшими точками волны, обладающими
одинаковой фазой (в данный момент времени).
(По определению длина волны – путь точки на поверхности фронта,
пройденный за время, равное периоду колебаний «осциллятора»
так, λ = V /
V=c/n – скорость света в среде,
оптическая частота.
n 41– показатель преломления,
-
Рассмотрим плоскую волну (11) и допустим, что фазы в точках и
одинаковы. Тогда в любой момент времени должно соблюдаться равенство
.
Это может быть лишь в том случае, если
, т. е.
.
k принято называть «волновым числом», (не путать с волновым вектором k)
Для простоты будем рассматривать монохроматические плоские волны, однако
результаты, которые мы получим, будут справедливы для любых плоских волн.
В однородной изотропной непроводящей среде векторы
и
изменяются в
соответствии с волновыми уравнениями (6) и (7):
.
(6)
,
(7)
при условии (12):
т. е.
. Если представить пространственно-временное
векторов E и H в виде плоских волн выражения принимают вид:
изменение
,
(14)
то эти выражения, безусловно, удовлетворяют уравнениям (7) и (6). Однако,
чтобы они удовлетворяли уравнениям Максвелла, на них следует наложить
еще дополнительные условия. Подставляя выражение (14) соответственно в
(3) и (4),:
,
(3)
,
(4)
получим:
42
,
.
Равенство нулю означает, что
и
.(Это позволяет считать,
что
и
взаимно перпендикулярны). Чтобы убедиться в этом твердо,
подставим выражения (14) в левые части уравнений (1) и (2) и получим:
,
.
Тогда уравнения (1) и (2)
,
(1)
.
(2)
примут вид
, или
,
(15)
, или
.
(16)
Достаточно умножить выражение (15) на
чтобы получить:
или выражение (16) на
,
.
(17)
Из полученных формул следует, что векторы ,
и
взаимно
перпендикулярны и образуют правую тройку векторов в том порядке, в
котором они написаны.
Вектор
определяет направление распространения волны. Векторы
и
колеблются
в
плоскости,
перпендикулярной
направлению .
Таким образом, электромагнитная волна в указанных условиях является
поперечно-поляризованной (направление колебаний перпендикулярно
направлению распространения).
В силу линейности уравнений Максвелла, или, что то же самое, в силу
суперпозиции полей, решением является любая сумма полей, у которых
векторы
и
лежат в указанной плоскости.
Еще раз отметим, что уравнения электромагнитной волны (14) записаны в
комплексной форме.
Вид этих уравнений для плоских волн в тригонометрической форме:
E = E0
– kr), Н = Н0
– kr).
43
ТЕОРИЯ ДИФРАКЦИИ КИРХГОФА-ЗОММЕРФЕЛЬДА
1. Интегральная теорема Гельмгольца—Кирхгофа
Перед тем как перейти к доказательству центральной теоремы теории
дифракции, вспомним формулировку теоремы Грина и определение функций
Грина.
Теорема Грина. Пусть U(P) и G(P) — две произвольные комплексные
функции пространственных координат в точке Р, а S — поверхность, окружающая объем V. Если эти функции, а также их первые и вторые частные
производные однозначны и непрерывны внутри указанного объема и на поверхности, его окружающей, то

U
G 
  G U  U  G  dV    G n  U n ds ,
2
2
(1)
V
где д/дп — обозначает частную производную в каждой точке поверхности по
внешней нормали в этой точке. Пользуясь этой теоремой, нужно все время
помнить об условиях, накладываемых на вид функций и форму поверхности.
Функции Грина. По определению функцией Грина называется решение
дифференциального уравнения, в правой части которого стоит дельта-функция. С точки зрения физики это означает, что функция Грина есть решение
задачи с точечным источником. В качестве примера можно привести волновое
уравнение и его решение. Если в волновом уравнении в правой части стоит
(r), то его решением является сферическая волна, так как в однородном
пространстве точечный источник излучает волну со сферическим волновым
фронтом.
Интегральная теорема Гельмгольца—Кирхгофа. Кирхгоф сформулировал
теорему,
которая
определяет
значение
поля
в
произвольной
точке
пространства через значение поля и его градиента на поверхности, ее окружающей. (Впервые она была доказана в акустике Гельмгольцем.)
Применим
(1) к объему V, окруженному поверхностью S. Внутри этого
объема находится точка Р0 ( Рис.2). Сам объем и действующее электромагнитное поле U(P) удовлетворяют условиям теоремы Грина. Выберем функцию
Грина G(P) в виде сферической волны, что соответствует нахождению
точечного излучателя в точке Р0. Это функция Грина для свободного пространства. В произвольной точке P1 ее значение равно
G  P1 
exp  jkr01 
r01
,
44
(2)
где через r01 обозначена длина вектора r01 из точки Р0 в точку P1. В нашем
случае не удовлетворяются требования, налагаемые на функцию G(P) условиями теоремы, так как при стремлении к нулю длины г01 функция G(P1) стремится к бесконечности. Окружим точку Р0 сферой малого радиуса
и
рассмотрим объем V' заключенный между поверхностями S и S . В этом
объеме условия теоремы Грина выполняются, надо только помнить, что поверхность S', окружающая объем V' стала неодносвязной (S'= S + S ) и
нормаль к поверхности на ее сферической части направлена внутрь сферы.
Рис.2. К выводу интегральной теоремы Гельмгольца— Кирхгофа
Любая электромагнитная волна, распространяющаяся в регулярной области
пространства, должна подчиняться волновому уравнению (в данном случае
уравнению Гельмгольца (2.19)). Поэтому и искомое решение — функция U(P)
и функция Грина свободного пространства G(P) должны подчиняться этому
уравнению.


 k 2  U  P   0;

2
 k 2  G  P   0.
2
(3)
Из этих уравнений следует, что
2G  P   k 2G  P  ; 2U  P   k 2U  P  .
Подставляя эти выражения в правую часть (1), получаем
  G U  U  G  dv   GUk
2
2
V
2
 UGk 2  dv  0 .
V
Однако это означает, что и левая часть в (1) также равна нулю:

U
G 
  G n  U n  ds  0 ,
s
или
G 
G 
 U
 U
  G
U
U
 ds    G
 ds .
n
n 
n
n 
S 
S 
(4)
Для дальнейшего рассмотрения необходимо записать явное выражение для
производной по нормали от функции Грина G(P):

G
1  exp  jkr01 
,
 cos  nr01   jk  
n
r01 
r01

45
(5)
где cos(nr01) — косинус угла между направлением внешней нормали п и
вектором r01, соединяющим точки Р0 и P1. В частном случае, если последняя
точка лежит на S , то cos(nr01) = - 1, тогда (2) и (5) принимают вид
G  P1  
exp  jk  

;
G  P1 
n

exp  jk    1

  jk  .



Если
(6)
U(P) и ее производной в точке Р0 ,
можно записать:

U
G 
  G n  U n  ds 
s
(7)
 G  P0  exp  jk  
exp  jk    1

42 
 U  P0 
 4U  P0  .
  jk  



  0
 n
При выводе этой формулы учитывалось, что при стремлении
к нулю,
площадь сферы S уменьшается и функцию U(P) можно считать постоянной и
равной ее значению в точке Р0 .
Подставив (7) в (4), можно получить решение интегральной теоремы
Гельмгольца—Кирхгофа в виде
U P0  

1 
  exp  jkr01   
 U exp  jkr01 
U


  ds.

4 S 
r01
n 
r01
 n


(8)
2. Дифракция на плоском экране
Рассмотрим теперь дифракцию электромагнитной волны на плоском, тонком,
бесконечном,
непроводящем
экране
с
отверстием,
воспользовавшись
теоремой, доказанной в предыдущем параграфе ( Рис.3). Волна падает на экран слева направо, и необходимо найти возмущение за экраном в точке P0 .
Воспользуемся интегральной теоремой и выберем в качестве поверхности
интегрирования сферу радиусом R с центром в точке Р0 . Там, где сфера
касается экрана, она обрезается его поверхностью. Если обозначить часть
плоскости, усекающую сферу как S1, а оставшуюся часть сферы как S2, то при
использовании
(8) необходимо интегрировать по составной поверхности
S=S1+S2:
U  P0  
G 
 U
G U

 ds .
n
n 
S  S1  S2 

(9)
В этой формуле функция G имеет вид, определяемый (2).
Увеличиваем радиус сферы. При этом поверхность интегрирования все более
и более становится похожей на полусферу. Функции U и G с ростом радиуса
46
сферы уменьшаются пропорционально 1/R, поэтому можно предположить, что
подынтегральное выражение стремится к нулю. В этом случае интегрирование
по поверхности полусферы S2 должно было бы давать нулевой вклад в
интеграл
(9). Однако это неочевидно, так как площадь поверхности
полусферы растет как R2 и неясно, какой же из факторов является определяющим. Необходим дополнительный анализ выражения (9).
На поверхности S2 функция
G
exp  jkR 
R
(10)
.
Из выражения (6) следует, что производная функции G
G 
1  exp  jkR 
  jk  
 jkG, при R   .
n 
R
R
(11)
Рис. 4.3. Дифракция на плоском экране
Преобразуем (9), перейдя от интегрирования по поверхности полусферы к
интегрированию по телесному углу, который на нее опирается,
 U
 U


 G n  U  jkG  ds   G  n  jkU  R d,
S2
2
(12)

— телесный угол с вершиной в Р0 , стягиваемый поверхностью S2.
Величина |RG| равномерно ограничена на S2, поэтому полный интеграл будет
стремиться к нулю при радиусе сферы, стремящемся к бесконечности, в том
случае, если выполняется условие
 U

lim R 
 jkU   0
 n

(13)
R 
равномерно во всем телесном угле.
Условие (13) носит название требования Зоммерфелъда для излучения. Оно
удовлетворяется, если функция U стремится к нулю со скоростью, по меньшей
мере равной той скорости, с которой расходится сферическая волна. Так как
волна, падающая на отверстие, всегда есть сферическая волна или набор таких
волн, то можно считать, что интеграл по полусфере действительно стремится к
нулю.
47
Таким образом, интеграл (9) может быть записан в виде
U  P0  
1  U
G 
 n G  U n  ds.
4 

S1 
(14)
Для того чтобы получить окончательную формулу дифракции на плоском
экране, необходимо определить граничные условия. Одновременно вспомним,
что экран непрозрачен всюду, кроме отверстия
. Граничные условия были
определены Кирхгофом и носят его имя:
1) в отверстии
(см. Рис.3) амплитуда поля U и ее производные такие же, как
если бы экрана не было вообще;
2) на поверхности S1 вне отверстия амплитуда поля U и ее производные равны
нулю.
С учетом граничных условий Кирхгофа (14) имеет вид
U  P0  
1  U
G 
 n G  U n  ds.
4 

 
(15)
Результат достаточно простой и понятный, так как, конечно, основной вклад в
поле за экраном будет давать участок отверстия. Однако это не всегда
справедливо. Присутствие экрана будет неизбежно вызывать возмущение поля
в отверстии, кроме того, тень за экраном никогда не будет резкой, так как поле
проникает за экран на расстояние в несколько длин волн. Но если отверстие
велико, а длина волны достаточно мала, то оба условия Кирхгофа
справедливы, а результаты, рассчитанные с помощью
(15), хорошо
согласуются с данными эксперимента.
3. Формула дифракции Френеля—Кирхгофа
Дифракционные эффекты слабо сказываются на малых расстояниях от
препятствия. Поэтому рассмотрим вначале случай, когда расстояние r01 много
больше длины волны, т. е. k >> 1/r01. В этом случае выражение для
производной от функции Грина (6) может быть преобразовано к виду
G  P1 
n
exp  jkr01 

1  exp  jkr01 
 cos  n, r01   jk  
 jk cos  n, r01 
,
r01 
r01
r01

(16)
где cos(n, r01) — косинус угла между вектором г01 и вектором внешней нормали к поверхности интегрирования, т.е. нормали к экрану. Подставим (16) и
явный вид функции G в (15).
48
1 exp  jkr01   U

U  P0  
 jkU cos  n, r01  ds.


4 
r01
 n

(17)
Теперь предположим, что экран с отверстием освещается сферической волной,
исходящей из точечного источника, расположенного слева от экрана в точке
Р2 ( Рис.4). Расстояние от источника до экрана равно r21. Тогда поле в
отверстии определяется следующим выражением:
U  P1  
A exp  jkr21 
r21
(18)
,
где А — коэффициент пропорциональности.
Подставив это выражение в (18), получим с учетом того, что r21 >>
U  P0  
A exp  jk  r21  r01    cos  n, r01   cos  n, r21  

 ds.
j 
r21r01
2



(19)
Этот результат, справедливый только при освещении экрана точечным
источником, называется формулой дифракции Френеля—Кирхгофа. Отметим,
что этот интеграл уже полностью определен, в нем нет неизвестных функций,
а те, что есть, легко вычисляются.
Еще одно замечание. Это выражение симметрично по отношению к
отражению: если поменять местами точки Р0 и Р2 , то результат не изменится.
Принцип такой взаимности был сформулирован Гельмгольцем.
Можно
интерпретировать
формулу
дифракции
Френеля—Кирхгофа
и
несколько иным образом, если переписать выражение (19):
U  P0    U '  P1 

exp  jkr01 
r01
ds,
где
U '  P1  
1  A exp  jkr21    cos  n, r01   cos  n, r21  


.
j 
r21
2


Рис.4. Дифракция сферической волны на плоском экране
Если исходить из этого выражения, то можно считать, что поле в точке P0
создается бесконечным множеством сферических волн, исходящих из точечных источников, находящихся в пределах отверстия, и имеющих ампли49
туду U´(P1). Амплитуда каждого вторичного
источника пропорциональна
амплитуде падающей волны, но отличается от нее следующим: во-первых,
есть множитель 1/ , во-вторых, происходит уменьшение амплитуды за счет
коэффициента наклона, который никогда не превышает единицы и всегда
больше нуля, в-третьих, фаза излучаемой волны отличается от фазы падающей
волны на
/2. Этот факт и соответствует предположению Френеля о фазах
источников. Таким образом, последняя интерпретация формулы Френеля—
Кирхгофа математически описывает принцип Гюйгенса—Френеля для случая
дифракции на плоском экране.
4. Формулировка Зоммерфельда задачи дифракции на плоском экране
Рассмотренная выше теория Кирхгофа дает очень точные результаты, однако
она внутренне противоречива. Противоречия кроются в граничных условиях,
которые были приняты для поля в плоскости экрана. Дело в том, что условия
отсутствия поля и его производной по нормали за экраном вне отверстия
приводят к невозможности существования поля вообще с математической
точки зрения. Существует известная теорема теории потенциала, которая
гласит, что если сама функция и ее производная тождественно равны нулю на
каком-то участке поверхности, то эта функция тождественно равна нулю во
всем пространстве. Физически это тоже понятно: если в крайней точке этого
участка поверхности сама функция и ее производная равны нулю, то почему
что-то должно появиться в соседней точке за краем? С другой точки зрения,
если учесть волновую природу света, совершенно очевидно, что край
отверстия не может не возмутить поле в отверстии, да и край тени не может
быть абсолютно резким.
Зоммерфельд предложил обойти это противоречие, изменив граничные
условия и налагая требования только на саму функцию или ее производную.
При этом все выводы и результаты должны остаться неизменными. С этой
целью он видоизменил функцию Грина, сделав ее либо симметричной, либо
антисимметричной:
G_ 
exp  jkr01 
r01

exp  jkr '01 
r '01
(20)
.
50
Рис.5. Симметризованная функция
Пояснить структуру этой функции можно с помощью Рис.5. Симметрично
точке Р0 относительно экрана расположена точка Р'0 , т.е. имеются два точечных источника, формирующих функцию Грина, причем фазы волн,
испускаемые этими источниками, одинаковы. Производная новой функции
Грина будет сдвинута на 180°:

G _
1  exp  jkr01 
 cos  n, r01   jk  

n
r01 
r01

(21)

1  exp  jkr '01 
 cos  n, r'01   jk 
.

r '01 
r '01

Здесь r'01 — расстояние от второго источника до поверхности экрана.
Если точка Р1 находится на поверхности экрана, то r01 = r'01 , cos (n, r01) = -cos
(n, r'О1) и
G _  P1   0;


G _  P1 

1  exp  jkr01  
 2cos  n, r01   jk  
.
n
r01 
r01


Из
(22)
(22) видно, что отпала необходимость введения жестких граничных
условий на функцию и на ее производную одновременно и имеющиеся противоречия сняты. Следует отметить, что можно было бы ввести симметричную функцию Грина G+, что привело бы к равенству нулю не функции Грина,
а ее производной в плоскости экрана.
Конечно, при использовании видоизмененной функции Грина изменится и
формула дифракции Френеля—Кирхгофа, она примет вид
U  P0   

Формула
exp  jk  r21  r01  
r21r01
cos  n, r01  ds.
(23)
(23) отличается от прежней формулы Френеля—Кирхгофа
(19)
только коэффициентом наклона и называется формулой Зоммерфельда.
До сих пор при анализе дифракции на плоском экране рассматривался вариант, когда он освещается одним точечным источником. В общем случае
51
освещение экрана осуществляется протяженным источником. Однако этот
протяженный источник может быть представлен в виде набора точечных ис-
точников, каждый из которых формирует свою собственную картину дифракции, которые складываются на выходе, при необходимости с учетом
фазы. При таком рассмотрении можно представить (21) в виде интеграла
суперпозиции
U  P0    h  P0 , P1 U  P1  ds,
(24)

где
h  P0 , P1  
1 exp  jkr01 
cos  n, r01  .
j
r01
Подобное представление является достаточно наглядным и будет использовано далее. Следует помнить, что интеграл суперпозиции работает
только для линейных систем, что справедливо для электромагнитных полей и
линейных сред.
До сих пор рассматривались некие точечные источники, на которые разбивались светящиеся поверхности. Однако это только математическая модель,
помогающая рассмотреть дифракционные явления. То же самое можно
сделать и альтернативным способом. В 1802 г. Юнг предложил формулировку
теории дифракции, основывающуюся на интегральном взаимодействии поля с
экраном. По его модели картина дифракции формируется как суперпозиция
волны, прошедшей через отверстие в экране без взаимодействия с ним, и
волны, которая взаимодействовала с краем отверстия. В силу того, что
источником дифракции является физический объект — край отверстия,
данный подход является очень корректным. Строгая теория дифракции
подтверждает это предположение. Однако выводы итоговых формул в этом
случае довольно громоздки, хотя, естественно, результат будет тем же самым.
4.2. УГЛОВОЙ СПЕКТР ПЛОСКИХ ВОЛН
В гл. 1 уже были сформулированы основные понятия двумерного преобразования Фурье применительно к оптическим системам. Активно применяемые в теории информации, радиотехнике и других областях современной
науки и техники преобразования Фурье всюду позволяют построить понятные
модели явлений, облегчить синтез сложных систем.
52
Как уже говорилось, в оптике используется
преимущественно двумерная
форма интегралов Фурье с преобразованием двух поперечных пространст-
венных координат. Если анализируемая волна имеет вид U(x, у, z), то преобразование Фурье (часто говорят Фурье-образ) может быть записано следующим образом:
A0  f x , f y , z     U  x, y, z  exp   j 2  f x x  f y y   dx dy
(25)

и соответственно обратное преобразование Фурье будет
U  x, y, z     A0  f x , f y , z  exp   j 2  f x x  f y y   df x df y .
(26)

Отметим, что в используемой форме записи прямое и обратное преобразования Фурье отличаются только знаком показателя экспоненты.
Предположим, что волна, созданная некоторой произвольной системой
монохроматических источников и распространяющаяся вдоль оси z, достигает
плоскости ху (z = 0). Комплексное поле в этой плоскости описывается функцией U(x, у, 0). Нашей целью является расчет поля U(x, у, z) в точке (х, у, z).
Проанализируем (26). С этой целью запишем математическое выражение для
плоской волны, распространяющейся в пространстве в направлении (нормаль
к
волновому
(
):
фронту),
определяемом
направляющими
косинусами
 2

B  x, y, z   exp  j  x  y  z  ,
 

(27)
где
  1   2  2 .
Поэтому в плоскости z = 0 экспоненциальную функцию (стоящую под
интегралом в выражении (24)) можно рассматривать как плоскую волну с
направляющими косинусами
  f x ;
  f y ;




2 
2
1   f x    f y  .

(28)
При такой записи (26) представляет собой суперпозицию плоских волн с
комплексными амплитудами вида A0(fx, fy) dfx dfy (причем fx
=
/ , fy
), каждая из которых распространяется по своему направлению.
Иными словами, любое распределение излученияв произвольной плоскости
может быть представлено в виде набора плоских волн, каждая из которых
распространяется по своему направлению со своей амплитудой.
53
В
новых
переменных
угловой
спектр
плоских
волн,
распределение излученияв плоскости z = 0, записывается в виде
составляющих


 

A0  ,     U  x, y,0  exp  j 2  x 

 




y   dx dy .

(29)
Теперь необходимо переместиться в плоскость z
между спектром плоских волн в начале координат и в этой плоскости:

 
  

A0  , , z     U  x, y, z  exp  j 2  x  y   dx dy .
 
  



(30)
Запишем обратное преобразование Фурье

   
  

U  x, y, z     A  , , z  exp  j 2  x  y   d d .
   
  



2
(31)
U + k2U = 0 (поскольку в рас-
сматриваемой области пространственных источников света нет), подставив в
него (31):
d 2      2 
  
A  , , z     1   2  2  A  , , z   0.
2
dz       
  
2
(32)
Частное решение этого уравнения можно записать в виде
  
  
 2
A  , , z   A0  , , z  exp  j
  
  
 
Если
2
+

1   2  2 z  .

z вдоль
2
оси проявляется только в изменении ее фазы относительно других плоских
волн, идущих под другими углами. Это понятно, так как они проходят
различные пути между плоскостями z = 0 и z
0. Если же
2
+
2
0, то
волны сильно затухают.
Использование разложения в спектр плоских волн весьма широко распространено в оптике при анализе прохождения света через сложные системы.
Как правило, проанализировать прохождение одной плоской волны через них
достаточно просто. Поэтому на входе системы разлагают начальное
распределение излучения в спектр плоских волн, затем находят решение для
произвольной плоской волны, а результирующее распределение излучения на
выходе получается как сумма тех же плоских волн, но с измененными фазами.
1. Элементы теории распространения электромагнитного излучения
в приближении скалярной теории дифракции. Интеграл Кирхгофа –
Френеля
Рассмотренные здесь вопросы приводят к 54
результатам и выводам, справедливым при
следующих основных ограничениях:

Электромагнитное излучение – монохроматическое, когерентное.

Выводы справедливы, в основном, для спектрального диапазона длин волн 0.3 Мкм – 1
См. Т.е. речь идет об ультрафиолетовом, оптическом, инфракрасном и радио- поддиапазонах.
Некоторые положения справедливы и для акустического излучения. Это выделяется в
отдельных комментариях.
1.1 Дифракция плоской волны на дифракционной решетке
1.1.1 Однородные плоские монохроматические волны
Ранее было показано, что любое решение волнового уравнения вида
(3)
представляет собой плоскую волну, так как в каждый момент времени
величина
постоянна во всех точках плоскости, задаваемой векторным уравнением в виде
скалярного произведения
,
где
– радиус-вектор точки
– единичный вектор
;
нормали к плоскости, координаты которого определяются направляющими косинусами
(рис. 1). .
Рис. 1
Иначе говоря, плоская волна, фаза которой постоянна во всех точках некоторой плоскости,
имеет плоский волновой фронт.
Общее решение волнового уравнения в виде (3), выражающее плоскую волну, которая
распространяется в направлении вектора
со скоростью
, имеет вид
(4)
Аргумент функции
и
не меняется при замене величин
и t на величины
соответственно. Физически это означает, что возмущение
, которое в момент
времени t было в плоскости, находящейся на расстоянии d от начала координат, в более
поздний момент времени
расстоянии
оказывается в плоскости, расположенной уже на
от начала координат. Вводя замену t нa
и учитывая, что
55
для однородной плоской волны
, получим скалярное комплексное
выражение для электрического (магнитного) поля однородной плоской монохроматической
волны
.
(5)
где
– длина волны в среде с показателем преломления n.
;
Ранее были рассмотрены, вопросы, касающиеся понятию пространственная частота.
Поскольку пространственная частота может определяться по-разному, вернемся к этому
понятию. При этом некоторые опредаеления в силу их важности рассматриваются повторно
и более подробно.
Длину волны
(6)
называют приведенной длиной волны (соответствует распространяющейся в вакууме
монохроматической волне той же частоты). Вектор
или
для вакуума
,
направленный вдоль единичного вектора нормали (рис. 1.4), называют волновым
вектором. Его длину
, соответственно для вакуума
, называют
волновым числом. Волновой вектор является обобщенным пространственным аналогом
временной угловой частоты
.
Так как выражение (5) не изменяется при замене
на
то
, является
пространственным периодом плоской волны. Для задания ориентации пространственных
гармонических осцилляции в плоской волне на практике очень удобно ввести векторы
пространственной частоты
,
,
направления которых совпадают с направлением распространения
(7)
, а длины
соответственно равны
,
(8)
Они задают число пространственных периодов (осцилляций) в волне, укладывающихся на
единице длины, 1/мм, соответственно в среде или в вакууме, и по аналогии с временной
частотой
называются пространственными частотами. Это еще более углубляет
аналогию между волновым вектором
и угловой частотой
.
В итоге комплексную амплитуду однородной плоской монохроматической волны можно
представить в виде
(9)
В соответствии с (4) фаза
координат, а фаза
56
увеличивается с ростом расстояния d от начала
уменьшается с ростом времени t. Выбор такого правила
знаков в плоской волне обусловлен описанием ее распространения в направлении вектора
. Он не имеет существенного значения, так как практический интерес представляет не
абсолютная величина фазы, а разность фаз. В то же время в рамках выбранного правила
знаков процесс распространения плоской волны сводится к следующему. Для любой точки
некоторой плоскости
полная фаза волны в момент времени t постоянна и равна
. В более поздний момент времени
фаза будет иметь то же значение на большем расстоянии
, так как
полная
от начала координат
, в то время как на прежнем
расстоянии d она уменьшается. В результате плоский волновой фронт перемещается в
пространстве в направлении, которое в зависимости от специфики задачи можно
охарактеризовать одним из трех коллинеарных векторов – единичным вектором нормали
, вектором пространственной частоты
или волновым вектором
(рис. 1).
Таким образом, однородная плоская монохроматическая волна является тем важным
частным случаем комплексного временного гармонического сигнала, который позволяет с
единых
позиций
рассматривать
частотно-временные
и
пространственно-частотные
гармонические осцилляции произвольной монохроматической электромагнитной волны,
представляемой в виде суммы плоских волн. Это в свою очередь служит первым шагом на
пути создания общей частотной модели при описании множества S входных сигналов
набором плоских волн. Рассмотренное ранее решение волнового уравнения для
сферических во многих практических случаях рассматривается в параксиальном
приближении. Параксиальное приближение для сферической волны имеет место в т о м
случае, когда г2 > > x2 + y2 .
.
√𝑥 2 + 𝑦 2 + 𝑧 2
= 𝑧√1 +
𝑥2 + 𝑦2
2𝑧 2
Воспользуемся пкрвыми двумя слагаемыми в разложении бинома Ньютона:
𝑧√1 +
𝑥 2 +𝑦 2
2𝑧 2
= z + (x2 + y2)/2z
При этом комплексная амплитуда сферической волны в
U(x,y,z) ≈
𝐴
exp(−𝑗𝑘𝑧) exp(−𝑗𝑘
𝑧
(15)
параксиальном приближении:
( 𝑥2 + 𝑦 2 )
2𝑧
)
1.1.2 Вывод интеграла Кирхгофа
Проанализируем дифракцию
распределением
волны на транспаранте с периодическим синусоидальным
амплитудного
пропускания.
Подобные
транспаранты
называют
дифракционными решетками, Пусть плоская
57 излучениеовая волна амплитудой А0,
распространяющаяся в направлении положительной полуоси z, падает на транспарант,
находящийся в плоскости z = 0. Допустим» что транспарант имеет амплитудное пропускание
tz=a
(x,zу) = t0 + t1 cos (2πηy),
(10)
являющееся периодической функцией от у с пространственной частотой η, а t0 и t1 —
Р
и
с
вещественные постоянные. При t0
> t1 > 0 транспарант не вносит фазового сдвига.
Непосредственно за транспарантом комплексная амплитуда волны:
.
1
.
5
.
Рис. 2.
Рис. 3.
Первый член данного выражения описывает плоскую волну, распространяющуюся вдоль оси z,
как и падающая волна, второй и третий члены — плоские волны, направления
распространения которых с осью z составляют углы φ1 и φ2 , причем
φ1 = - φ2 = arcsin (λη)
(рис. 3).
Таким образом, моделируеncя, что в результате дифракции часть падающей на транспарант
волны отклоняется от первоначального направления распространения. (и эта модель
адекватна экспериментальным результатам)
С помощью соотношения
с учетом того, что:
где:
можно определить комплексную амплитуду излучения при любом удалении от транспаранта,
например при
58
(11)
Для первого члена выражения ζ – η = 0, для второго и третьего членов , ζ = 0. Из (11) следует,
что если λ η > 1 ,
то возникают поверхностные волны. Они будут затухающими при
λ > 1 / η , т. е. когда длина волны больше периода дифракционной решетки, поскольку при
этом √1 − 𝜆2 𝜂2 становится мнимой величиной, а
exp [—jkd (1 — 𝜆2 𝜂2 )!1/2] — экспоненциальным множителем, убывающим с увеличением
d.
Амплитудное пропускание двумерной дифракционной решетки в общем случае описывается
комплексной периодической функцией двух переменных х н у . Однако его также легко
представить в виде суммы простейших синусоидальных функций путем разложения в ряд
Фурье:
Дифрагированная
на
таком
транспаранте
излучениеовая
волна
представляет
собой
суперпозицию бесконечного числа плоских волн с амплитудами, пропорциональными
соответствующим коэффициентам разложения t m n и направлениями распространения,
определяемыми cos αn = λζn и cos βn = ληn
Следовательно,
суммарная
амплитуда
дифрагированных волн в плоскости z = d
В общем случае амплитудное пропускание дифрагирующего объекта является комплексной
непериодической функцией двух переменных х и у , поэтому t (x, у)
заменяют интегралом Фурье. Комплексную амплитуду дифрагированной волны в плоскости z
= d при этом также выражают с помощью интеграла
(12)
где Т (ζ,, η) — преобразование Фурье от t (х, у ), причем интегрирование производят в
области, удовлетворяющей неравенству ζ2 + η2 < 1/λ2 (вне этой области волны быстро
затухают при удалении от транспаранта).59Следовательно, можно сделать следующее
заключение: если плоская волна амплитудой А1 распространяющаяся в направлении оси z,
падает на помещенный в плоскости z = 0 транспарант с амплитудной функцией
пропускания t (х, у) у то спектр комплексной амплитуды в плоскости z = d имеет вид:
(13)
Для параксиальных волн (<<1), пользуясь приближением
,
справедливым при малых значениях ζ, и η выражение (13) можно представить следующим
образом:
Ввиду того, что фаза φ =
πλd(ζ,2 + η 2) в этом выражении является параболической
функцией пространственных частот, это приближение называют параболическим.
Согласно правилу Рэлея искажение фазы волны не должно превышать π/2, т. е.
устанавливаются границы применимости параболического приближения:
Рис.4. Разрешение по Рэлею:
а – абсолютный критерий разрешения; б – критерий Рэлея
Разрешение по Рэлею. Этот критерий определяет способность прибора изображать
раздельно два близко расположенных точечных предмета и равен минимальному
расстоянию
σ R между ними.
В зависимости от принятого правила,
отличие,
разрешение
правило связывают с
интенсивности
по
которому
устанавливается
указанное
по Рэлею может иметь различное значение. Обычно решающее
относительной
60
величиной
ε
провала
в
распределении
в изображении двух точек (рис. 4). При ε=0 получаем абсолютный
критерий разрешения σ 0.
Правило Рэлея требует:
Центральный максимум взображении одной точки должен приходится на первый минимум
в изображении другой.
Разрешение по Рэлею удовлетворительно характеризует
качество
изображения
астрономических телескопов, спектральных приборов, для которых предметами являются
близко расположенные точки или линии..
Решение задачи дифракции можно представить также с помощью интеграла Френеля —
Кирхгофа:
.
(14)
Где
(рис. 5) x0, у 0 и х, у — координаты точек,
принадлежащих плоскостям z = 0 и z = d. Угол между положительным направлением
оси z и отрезком прямой r o d , cos θzr называют коэффициентом наклона.
Рис. 5
Интеграл (3) является математическим выражением известного принципа Гюйгенса —
Френеля.
Принцип Гюйгенса — Френеля
Принцип Гюйгенса — Френеля — основной постулат волновой теории, описывающий и
объясняющий механизм распространения волн, в частности, излучениеовых.
Каждый элемент волнового фронта можно рассматривать, как центр вторичного
возмущения, порождающего вторичные сферические волны, а результирующее
излучениеовое поле в каждой точке пространства будет определяться интерференцией
этих волн.
61
Рефракция волн по Гюйгенсу
.
Дифракция волн по Гюйгенсу
2.
Дифракционные формулы Френеля и Фраунгофера
Рассмотрим дифракцию излучения, падающего на непрозрачный экран с отверстием
произвольной формы. Отверстие в экране называют апертурой. В зависимости от
удаленности источника излучения и плоскости наблюдения от дифрагирующего экрана
различают зоны дифракции Фраунгофера и Френеля. Дифракция Фраунгофера наблюдается
в дальней зоне, удаленной от дифрагирующего экрана на расстояние, во много раз
превышающее размеры апертуры. Дифракция Френеля имеет место в ближней зоне,
распространяющейся до зоны дифракции Фраунгофера, как это показано на рис. 6.
Дифракция Фраунгофера по существу является предельным случаем дифракции Френеля
при больших расстояниях от экрана. Заметим, что зона дифракции Френеля также
начинается на некотором расстоянии от экрана. Непосредственно за апертурой вблизи
экрана находится область тени (рис. 6). Здесь и далее будем предполагать, что размеры отверстия на экране велики сравнению с длиной волны падающего излучения, а источник
излучения находится на таком расстоянии от экрана, что излучение, падающий на экран,
имеет практически плоский волновой фронт и постоянную амплитуду.
В общем случае апертура представляет собой транспарант с двумерной амплитуднойг
62
функцией пропускания t (х 0 , у 0 ). В частном случае апертура Sa является отверстием с
амплитудной функцией пропускания (Рис. 6):
t (х 0 , у 0 ) =
{
Данный случай важен, поскольку часто встречается при анализе оптических систем
хранения и обработки информации. (Голографические ЗУ). В любом из рассмотренных
случаев непосредственно за экраном при z = +0
Sa
Если провести мысленный эксперимент, поместив за экраном с отверстием лист бумаги, то,
отодвигая его от экрана, можно наблюдать развитие дифракционных процессов. При
близком расположении листа к экрану увидим достаточно четкое изображение отверстия,
которое будет постепенно размываться при увеличении расстояния от экрана до листа. В
этой связи есть смысл более внимательно рассмотреть те области, где влияние дифракции
уже достаточно велико. Эти области и называются областью дифракции Френеля
(дифракция в ближней зоне) и областью дифракции Фраунгофера (дифракция в дальней
зоне). На Рис.6 показана схема формирования изображения в дифракционной области.
Применим формулу Зоммерфельда, заменив в интеграле конечные пределы на бесконечные, считая, что вне отверстия функция U(x1, y1) = 0:
.
U  x0 , y0    h  x0 , y0 , x1 , y1 U  x1 , y1  dx1 dy1 ,

где
(15)
h  x0 , y0 , x1 , y1  
1 exp  jkr01 
cos  n, r'01  .
j
r01
63
Рис.7. Схема формирования изображения в дифракционной области
КОММЕНТАРИЙ: {Формула Зоммерфельда введена для устранения противоречий,
следующих из физики и теоремы потенциала:
Еесли сама функция и ее производная тождественно равны нулю на каком-то участке
поверхности, то эта функция тождественно равна нулю во всем пространстве.
То есть если в крайней точке этого участка поверхности сама функция и ее
производная равны нулю, то жесамое имеет место в соседней точке за краем. С другой
стороны, край отверстия не может не возмутить поле в отверстии. Кроме того,
край тени не может быть абсолютно резким.
Зоммерфельд предложил обойти это противоречие, изменив граничные условия и
налагая требования только на саму функцию или ее производную. При этом все выводы
и результаты должны остаться неизменными. С этой целью он видоизменил функцию
Грина, сделав ее либо симметричной, либо антисимметричной:
G_ 
exp  jkr01 
r01

exp  jkr '01 
r '01
.
Пояснить структуру этой функции можно с помощью рисунка:
Симметризованная функция
Симметрично точке Р0 относительно экрана расположена точка Р'0 , т.е. имеются
два точечных источника, формирующих функцию Грина, причем фазы волн,
испускаемые этими источниками, одинаковы. Производная новой функции Грина будет сдвинута на 180°:

G _
1  exp  jkr01 
 cos  n, r01   jk  

n
r01 
r01


1  exp  jkr '01 
 cos  n, r'01   jk 
.

r '01 
r '01

(1)
Здесь r'01 — расстояние от второго источника до поверхности экрана. Если
точка Р1 находится на поверхности экрана, то r01 = r'01 , cos (n, r01) = -cos (n, r'О1) и
G _  P1   0;


G _  P1 


1  exp  jkr01 64
 2cos  n, r01   jk  
.
n
r01 
r01


(2)
Из (2) видно, что отпала необходимость введения жестких граничных условий на
функцию и на ее производную одновременно и вышеотмеченнные противоречия сняты.
При использовании видоизмененной функции Грина, формула дифракции Френеля—
Кирхгофа примет вид
U  P0   
exp  jk  r21  r01  
r21r01

cos  n, r01  ds.
(3)
Формула (3) отличается от прежней формулы Френеля—Кирхгофа
только
коэффициентом наклона и называется формулой Зоммерфельда.
До сих пор при анализе дифракции на плоском экране рассматривался вариант, когда
он освещается одним точечным источником. В общем случае освещение экрана
осуществляется протяженным источником. Однако этот протяженный источник
может быть представлен в виде набора точечных источников, каждый из которых
формирует свою собственную картину дифракции, которые складываются на выходе,
при необходимости с учетом фазы. При таком рассмотрении можно представить
поле в виде интеграла суперпозиции
U  P0    h  P0 , P1 U  P1  ds,
(4)

где
h  P0 , P1  
1 exp  jkr01 
cos  n, r01  .
j
r01
Таким образом, противоречия снимаются}.
Наше приближение будет основываться на предположении, что z >> rmах (максимального
размера отверстия в экране). Область наблюдения в выходной плоскости также лежит
вблизи оси z и много меньше, чем z. В этих предположениях cos(n, r01) = 1 с погрешностью
не более 5 % (если угол не превышает 18°), в знаменателе
(15) r01 тоже будет лишь
незначительно отличаться от z. Тогда можно переписать вторую часть (15) в виде
h  x0 , y0 , x1 , y1  
1
exp  jkr01  . (16)
jz
Расстояние r01 в показателе экспоненты нельзя просто заменить на z, так как вследствие
того, что к велико, даже малое изменение r01 приведет к значительному изменению
экспоненты.
2.1. Приближение Френеля
Можно и далее упростить анализ, если заменить точное выражение для r01:
r01 
z 2   x0  x1    y0  y1   z
2
2
 x  x   y  y1 
1  0 1    0

 z   z 
2
2
его разложением в ряд.
В разложении оставим только два первых члена, считая, что величины, стоящие в скобках,
достаточно малы,
 1  x  x 2 1  y  y 2 
r01  z 1   0 1    0 1   .
 2  z  2  z  
65
(17)
При этом функция h принимает следующий вид:
h  x0 , y0 , x1 , y1  
exp  jkz 
j z
2
2 
 k
exp  j  x0  x1    y0  y1    .


 2z
(18)
В том случае, если z достаточно велико, решение соответствует приближению Френеля.
В приближении Френеля сферические волны заменяются поверхностями 2-го порядка. При
этом естественным образом налагаются ограничения на z, размеры отверстия, и т.д. Можно
провести оценку и показать, что для этого должно выполняться условие
z 3 
 
2
2 2
x0  x1    y0  y1   .


4 
(19)
Данное условие получается при условии малости следующего члена в разложении (18).
Подставим (18) в интеграл Кирхгофа:
U  x0 , y0  
exp  jkz 
j z
 k
 U  x , y  exp  j 2 z  x
1
1
0

2
2 
 x1    y0  y1    dx1 dy1

(20)
и разложим квадратичные члены в показателе экспоненты
U  x0 , y0  
exp  jkz 
j z
 k

exp  j  x02  y02  
2
z



 k
  U  x , y  exp  j 2 z  x
1
1
2
1

 2

 exp   j  x0 x1  y0 y1   dx1 dy1 .
 z


 y12    

(21)
Интеграл в (21) описывает распределение в ближней зоне дифракции, или зоне дифракции
Френеля. Если проанализировать структуру выражения
(21), то с точностью до
амплитудного и фазового множителей, не зависящих от координат выходной плоскости и
стоящих перед интегралом, распределение поля в выходной плоскости может быть
представлено как
 k 2

x1  y12  для частот f x  x0 z , f y  y0 z .

2
z


преобразование Фурье от функции U  x1 , y1  exp  j
Дополнительные результаты могут быть получены при рассмотрении не самого поля, а его
спектра. Для этого проведем преобразование Фурье от функции h:
H  f x , f y   exp  jkz  exp  jz  f x2  f y2  . (22)
Это выражение описывает эффект распространения волны в пространстве при дифракции
Френеля. Первый экспоненциальный множитель определяет общую фазовую задержку при
распространении на расстояние z, а второй — фазовую дисперсию, зависящую от
пространственной частоты по квадратичному закону.
2.2. Приближение Фраунгофера
Можно еще более ужесточить требования к расстоянию r01 до выходной плоскости,
отодвинувшись в дальнюю зону дифракции — зону дифракции Фраунгофера. Эта область
удовлетворяет следующему условию:
z 
k  x12  y12 
2
66
max
. (23)
Условие (23) определяет параметр малости при разложении величины r01 в ряд. При этом
квадратичный фазовый множитель в фигурных скобках (21) практически равен единице по
всему отверстию и амплитуда поля в выходной плоскости имеет вид
 k

exp  jkz  exp  j  x02  y02  
 2z

U  x0 , y0  
j z
(24)
 2

   U  x1 , y1  exp   j  x0 x1  y0 y1   dx1 dy1 .
 z


Без учета множителей перед интегралом, которые тем более несущественны при
вычислении интенсивности в изображении (при умножении на комплексно-сопряженное
выражение),
(24) представляет собой преобразование Фурье распределения поля в
отверстии для пространственных частот νx=x0/λz и νy=y0/λz.
Полученная формула и есть формула дифракции в приближении Фраунгофера. Следует
отметить, что в обычных условиях требования по дальности области наблюдения от экрана
достаточно жесткие. Так, для отверстия размером 2,5 мм при длине волны излучения 0,6
мкм расстояние до экрана должно быть более 15 м.
Оптические системы, выполняющие преобразование Фурье
С помощью сферической линзы можно создавать картину, являющуюся фурьеобразом входного изображения. Благодаря этому устройству, а также
возможности применения линз для формирования пучков излучения требуемой
конфигурации они находят широкое применение в оптических системах
хранения и обработки информации.
Рассмотрим простейшую оптическую систему (рис. 1), состоящую из одной
тонкой сферической линзы с фокусным расстоянием f помещенной в плоскости z
= 0, и расположенного вплотную к ней транспаранта с комплексным
амплитудным пропусканием
t (х0, у0).
67
Линзу называют тонкой, если луч, входящий в точку с координатами (x0, y0)
выходит из нее на противоположной поверхности в точке примерно с теми же
координатами. Это означает, что смещением луча внутри линзы можно
пренебречь:
линза
задерживает
фронт
падающей
волны
на
значение,
пропорциональное толщине линзы в каждой точке. Следовательно, тонкую
линзу можно рассматривать как транспарант, осуществляющий фазовую модуляцию и имеющий функцию пропускания вида
, где
функция Δφ(х, у) пропорциональна толщине линзы в точке с координатами (х,
у). Нетрудно показать, что
(1)
{………. Таким образом, свет в тонкой линзе проходит оптический путь,
пропорциональный толщине линзы в данной точке. Обратимся к рис. а.
Проведем две параллельные плоскости, прижатые к линзе с обеих сторон. Луч
А проходит через линзу оптический путь n
преломления материала линзы;
0
(где п —- показатель
0
— ее максимальная толщина), а луч В часть
пути между плоскостями проходит в воздухе, а часть — в стекле, поэтому
пройденный им оптический путь равен п (х, у) - (
0
-
(х, у)), где
(х, у) —
толщина стеклянной части линзы в соответствующей точке.
Рис. а. Линза как фазовая задержка
68
Этому оптическому пути соответствует изменение фазы световой волны,
равное
Тогда коэффициент пропускания линзы как объекта, сформированного двумя
параллельными плоскостями,
(1.1)
При этом мы учли, что линза абсолютно прозрачна, поэтому коэффициент
амплитудного пропускания равен единице, а все изменения содержатся в
показателе экспоненты.
Необходимо определить значение
(х, у). При этом мы будем учитывать
правило знаков: радиус кривизны поверхности считается положительным,
если эта поверхность выпуклая для луча, идущего слева направо. Разделим
линзу на две части (см. рис. а) и проанализируем их по отдельности.
Представим толщину линзы как сумму толщин двух ее половинок
(x,y)=
1(x,y)+
2(x,y).
Каждая из этих величин может быть выражена через
соответствующий радиус кривизны, как это видно из рис. а:
В уравнениях учитывался знак радиусов кривизны.
Складываем полученные величины и получаем толщину линзы в произвольной точке
(1.2)
Будем рассматривать только лучи, идущие под небольшими углами к оси
линзы (параксиальное приближение), поэтому в (1.2) корни можно разложить
в ряд, оставив только нулевой и первый члены ряда
Подставляя это разложение в (1.2), получаем
(1.3)
Теперь преобразуем к явному виду (1.4)69
Воспользовавшись формулой линзы, окончательно получим
………………………………………………………………………………………
….}
Таким образом, соответствующее тонкой сферической линзе комплексное
пропускание
(2)
Допустим, что на рассматриваемую оптическую систему (рис. 1) падает
плоская волна амплитудой A0, распространяющаяся в положительном
направлении оси z. Комплексная амплитуда света непосредственно вблизй
линзы справа от нее равна произведению функции пропускания транспаранта
и линзы:
(3)
Далее
волна
распространяется
в
свободном
пространстве,
поэтому
комплексная амплитуда света на любом расстоянии от линзы может быть
рассчитана с помощью интеграла Френеля — Кирхгофа.
Для расчета распределения комплексных амплитуд света на расстоянии z = d
от линзы воспользуемся приближением Френеля.
Тогда
(4)
70
Интегрирование производят по всей поверхности линзы. Подставим в (4)
выражение
(3),
опустив
несущественный
для
дальнейшего
анализа
постоянный фазовый множитель
ехр (— ikd),
(5)
В результате упрощения данного интеграла путем разложения квадратов (х
— х0)2 и (у — y0)2 , получим
(6)
71
Если d = f т. е. рассматривается распределение комплексных амплитуд
света в задней фокальной плоскости линзы, то выражение (6) еще более
упрощается и принимает следующий вид:
(7)
где
.
Интеграл в данном выражении представляет собой двумерное пре-
образование Фурье функции t (х, у) при условии, что функция t (х, у)
тождественно равна нулю за пределами поверхности линзы. Это условие
позволяет расширить пределы интегрирования до бесконечности, что и
требуется для преобразования Фурье.
Таким образом, если на тонкую сферическую линзу с примыкающим к
ней транспарантом падает плоская световая волна,то в задней фокальной
плоскости линзы образуется поле с распределением комплексных
амплитуд, пропорциональным произведению квадратичного фазового
множителя и фурье-образа функции пропускания транспаранта.
В тех случаях, когда важна только интенсивность света, квадратичный
фазовый множитель в выражении (1.48) не учитывают.
Эффект, обусловленный этим множителем, эквивалентен действию
тонкой рассеивающей (вогнутой) линзы с фокусным расстоянием - f, помещенной в плоскости z =f. Если в плоскость z=f поместить тонкую собирающую линзу с фокусным расстоянием f то этот фазовый множитель
будет компенсирован. В результате получают оптическую систему (рис.
1.8), выполняющую точное преобразование Фурье:
72
Предполагается, что за пределами поверхности транспаранта t (х, у) == 0.
Если линза имеет неограниченные размеры, а транспарант совершенно
прозрачен, т. е. t (х, у) =1, то
Следовательно, падающая на линзу плоская световая волна фокусируется в
точку на задней фокальной плоскости линзы. Линза конечных размеров
образует световое пятно малых, но все же конечных размеров, что и
наблюдается на практике.
Теоретические основы метода
1. Общие положения.
Голография (др.-греч. ὅλος — полный + γραφή — запись, изображение) — набор технологий
для точной записи, воспроизведения и переформирования волновых полей.
Оптическая голограмма одновременно выполняет три функции: функцию измерения и
регистрации амплитуды и фазы волнового фронта (запись информации), функцию хранения
результатов этого измерения (хранение информации) и функцию реконструкции волнового
поля (воспроизведение информации). Это сочетание оказалось замечательно удачным в
изобразительной голографии и в некоторых других применениях, например в
голографической интерферометрии.
Цифровая голография — это анализ, синтез и моделирование волновых полей средствами
цифровой вычислительной техники. Анализ полей — это измерение физических параметров
объектов по результатам регистрации в виде голограмм и иптерферограмм рассеянного ими
волнового поля. Синтез состоит в построении волнового поля объекта, заданного своим
73
математическим описанием или сигналом. Моделирование — изучение преобразования
полей
в голографических системах посредством исследования их цифровых моделей.
2. Запись голограммы.
Одна из возможных схем записи голограммы представлена на рис. 1. Лазерный пучок света
делится с помощью делителя BS на два пучка, один из которых с помощью зеркала М1 и
собирающей линзы L1 направляется на объект S, а второй пучок – опорный, с помощью
зеркала М2 и линзы L2 направляется непосредственно на фоторегистрирующую среду PD,
например, фотопластинку в обычной аналоговой голографии, или матричный фотоприемник
в цифровой голографии. Рассеянное (отраженное) объектом волновое поле также попадает
на фоторегистратор и интерферирует с опорной волной.
Рис. 1 Запись аналоговой голограммы
Записывается распределение интенсивности суммарного интерференционного поля в
плоскости фоторегистратора
Где US – распределение комплексной амплитуды объектного поля в плоскости
фоторегистратора; UR – распределение комплексной амплитуды опорного поля в плоскости
фоторегистратора:
74
где AS, AR – распределения амплитуды объектной и опорной волн, соответственно;
φS, φR – фазовые пространственные распределения вобъектной и опорной волнах.
Распределение интенсивности I называют голограммной структурой в формальном,
математическом представлении. В цифровой голографии численное представление I также
можно называть голограммной структурой или просто голограммой.
В обычной, аналоговой голографии фотопластинка после записи и соответствующего
химического процесса проявления и закрепления становится голограммой – дифракционным
оптическим элементом, амплитудное пропускание которого τ в условиях линейной записи
можно считать пропорциональным распределению интенсивности:
- для позитивного фоторегистратора, и
- для негативного фоторегистратора.
Коэффициенты γp и γn характеризуют контрастность процесса записи, а слагаемое τ0
определяет амплитудное пропускание голограммы при нулевой интенсивности.
В цифровой голографии регистрируемый фотоэлектрический сигнал up можно считать
пропорциональным распределению интенсивности I :
где сигнал up для простоты записан в виде непрерывной функции, тогда как в цифровой
голографии этот сигнал имеет дискретные значения в дискретном массиве пространственных
координат (xi, yj ).
Восстановление голограммы.
В обычной голографии для восстановления объектного волнового поля голограмма
освещается опорной волной (рис. 2), которая дифрагирует на голограмме, как на сложной
дифракционной решетке, и в дифракционном поле образуется (восстанавливается) объектное
волновое поле. Процесс освещения голограммы опорной волной формально записывается в
виде произведения амплитудного пропускания голограммы τ и комплексной амплитуды
освещающей волны UR:
75
Второе слагаемое в пропорционально комплексной амплитуде объектного поля US и
описывает восстановленную объектную волну, распространяющуюся в направлении от
объекта.
Если осветить голограмму сопряженной опорной волной, как это показано на рис. 2,
комплексную амплитуду которой следует представить в сопряженной форме UR*, то в
дифракционном поле за голограммой образуется сопряженное объектное поле US*,
распространяющееся в обратном направлении по отношению к объектному полю US на этапе
записи голограммы.
Рис 2 Восстановление голограммы.
Формально
процесс
восстановления
сопряженного
объектного
поля
определяется
следующим выражением:
где третье слагаемое определяет восстановленную сопряженную объектную
волну US, распространяющуюся в обратном направлении. Это волновое поле образует
действительное изображение объекта S в области его расположения на этапе записи
голограммы.
4. Дифракционные преобразования волновых полей.
76
Рассмотрим математическую модель преобразования волновых полей в голографических
системах. Чтобы не усложнять картину, ограничимся несамосветящимися непрозрачными
объектами и монохроматическим освещением.
Свойства объекта, определяющие его способность отражать и рассеивать падающее на него
излучение, описываются коэффициентом отражения излучения по интенсивности В (х, у, z)
или амплитуде β(х, у, z) — функциями координат на поверхности объекта.
Коэффициент отражения по амплитуде является комплексной функцией, которая может быть
представлена в виде:
b (х, у, z) = |b (х, у, z)| ехр[iβ(х, у, z)].
( 4.1)
Ее модуль |b| и фаза (β) показывают, во сколько раз изменяется амплитуда и соответственно
насколько изменяется фаза излучения в точке (х, у, z) поверхности тела после отражения.
Функции В и b связаны между собой соотношением
В = |b|2 = bb*,
( 4.2)
где * — знак комплексного сопряжения. Зная функцию b (х, у, z), уравнение поверхности
тела F (х, у, z) = 0 и распределение амплитуды и фазы падающего на объект света, можно в
принципе вычислить распределение амплитуды и фазы рассеянного света в произвольной
точке пространства.
Пусть А (х, у, z) ехр (iα(х, у, z)) — распределение амплитуды и фазы освещения на
поверхности объекта. Тогда поле на некоторой поверхности наблюдения можно описать с
помощью интегрального соотношения Кирхгофа
Г(ξ, η, ζ) = ∭𝐹(𝑥,𝑦,𝑧) 𝐴(𝑥, 𝑦, 𝑧)|𝑏(𝑥, 𝑦, 𝑧)| exp{𝑗[𝛼(𝑥, 𝑦, 𝑧) + 𝛽(𝑥, 𝑦, 𝑧)]} 𝑇 (х, у, 𝑧, 𝜉, 𝜂, 𝜁)𝑑𝜉𝑑𝜂𝑑𝜁
( 4.2)
где интегрирование производится на поверхности объекта F (х, у, z). Вид ядра этого
преобразования Т (х, у, z, ξ, η, ζ) зависит от пространственного расположения объекта и
поверхности наблюдения. Это преобразование в принципе обратимо:
b (х, у, z) = ∭𝑆 Г(𝜉, 𝜂, 𝜁)T’ Г(ξ, η, ζ) 𝑑𝜉𝑑𝜂𝑑𝜁
( 4.3)
Где T’ - оператор, взаимный Т, а интегрирование производится по поверхности наблюдения
S. Это выражение описывает процесс восстановления волнового поля.
77
Функцию Г(ξ, η, ζ) можно назвать математической голограммой. Задача синтеза голограмм
заключается в вычислении функции Г(ξ, η, ζ) по заданной функции b (х, у, z) и регистрации
результата в такой форме, которая допускала бы взаимодействие с излучением для
визуализации или восстановления b (х, у, z) в соответствии с ( 4.3). Задача анализа голограмм
состоит в выполнении преобразования ( 4.3).
Вычисление интеграла ( 4.2), ( 4.3) представляет собой в общем случае достаточно сложную
задачу. Ее удается решить только для очень простых объектов, заданных небольшим
количеством отдельных точек или линий. В общем случае приходится прибегать к
различного рода упрощениям.
Первое упрощение, к которому можно прибегнуть без большого ущерба для существа
проблемы, состоит в сведении трехмерной задачи к двумерной. Для этого поверхность
наблюдения считается плоской, а распределение амплитуды и фазы волны на поверхности
объекта заменяется по законам геометрической оптики распределением амплитуды и фазы
на плоскости, касающейся объекта или достаточно близкой к нему (чтобы при пересчете
амплитуды и фазы волны можно было пренебрегать дифракцией и пользоваться
геометрической оптикой) и параллельной плоскости наблюдения.
Тогда вместо ( 4.2) имеем
Г(ξ, η) ≈ ∬(𝑥,𝑦) 𝑏1 (х, у) Td(х, у, ξ, η)dxdy
( 4.4)
где b1 (х, у) — комплексная функция, полученная в результате пересчета амплитуды и фазы
поля, отраженного объектом, на плоскость (х, у), касательную к нему и параллельную
плоскости наблюдения (ξ, η); d — расстояние между этими двумя плоскостями.
Очевидно, если угол, под которым виден объект с поверхности наблюдения (угол охвата) и
площадь наблюдения малы, это естественная аппроксимация. Для задач, где угол охвата
должен быть велик, такой подход означает необходимость сведения их к задаче расчета при
малом угле охвата. При этом для реализации больших углов охвата поверхность наблюдения
можно разбить на небольшие фрагменты, аппроксимируемые плоскостями, и рассматривать
голограммы для отдельных фрагментов, каждая из которых представляет часть общего угла
и воспроизводит объект под своим ракурсом.
Ядро преобразования ( 4.4), связывающее распределение света на двух параллельных
плоскостях, имеет вид
78
Td(х, у, ξ, η) =
exp{2𝜋𝑗λ−1 √(𝑥−𝜉)2 +(𝑦−𝜂)2 +𝑑 2 }
( 4.5)
√(𝑥−𝜉)2 +(𝑦−𝜂)2 +𝑑 2
где λ — длина волны излучения.
Если геометрические размеры тела малы по сравнению с расстоянием d до плоскости
наблюдения, то это вместе с условием малости площади наблюдения приводит к
дальнейшему упрощению.
При
4λ
[(x – ξ)2 +(y – η)2] макс = θ2 макс < √ 𝑘𝑑
( 4.6)
где θмакс — максимальный угол (в радианах), под которым наблюдается объект с расстояния
d; к — коэффициент допустимой фазовой ошибки, равной π/к, в передаче аргумента
экспоненты в ( 4.5).
Td(х, у, ξ, η) ≈
exp{2𝜋𝑗λ−1 √(𝑥−𝜉)2 +(𝑦−𝜂)2 +𝑑2 }
( 4.7)
𝑑
В этом случае интеграл ( 4.4) переходит в интеграл Френеля:
Г(ξ, η) ≈ ∬(𝑥,𝑦) 𝑏1 (х, у) exp{ 2𝜋𝑗(λd)−1 (𝑥 − 𝜉)2 + (𝑦 − 𝜂)2 } dxdy
( 4.8)
Голограммы, описываемые этим соотношением, будем называть голограммами Френеля.
Если
𝜋(x 2 + 𝑦 2 )/λd << 1,
𝜋(𝜉 2 + 𝜂2 )/λd << 1
( 4.9)
так что этими составляющими фазы под интегралом в ( 4.8) можно пренебречь, возможно
дальнейшее упрощение. В этом случае ( 4.8) переходит в интеграл Фурье:
Г(ξ, η) ≈ ∬(𝑥,𝑦) 𝑏1 (х, у) exp{ 2𝜋𝑗(λd)−1 (𝑥𝜉) + (𝑦𝜂) } dxdy
( 4.10)
который соответствует дальней зоне дифракции (дифракции Фаунгофера). Соотношение
A.11) описывает также свойства линзы как оптического элемента, выполняющего
преобразование Фурье.
79
Этот случай имеет особое значение для систем оптической обработки информации благодаря
свойству инвариантности амплитуды преобразования Фурье относительно сдвигов по
координатам, которое позволяет в оптических устройствах реализовать операции типа
свертки.
Также операция преобразования Фурье, являясь распространенной в различных алгоритмах
цифровой
обработки
сигналов,
имеет
проработанные
алгоритмические
решения,
объединённые в пакете matlab в функциях fft, fft2 и fftn.
Таким образом, для цифрового моделирования голографических процессов основной
операцией является операция двухмерного прямого и обратного преобразования Фурье.
1. Уравнение Шредингера
Законы классической механики И. Ньютона и классической
электродинамики Дж. Максвелла оказались недостаточными для описания
процессов, в которых происходит взаимодействие отдельных атомов,
молекул. Открытия электрона – составной части атома – Дж. Томсоном,
атомного ядра Э. Резерфордом радикально изменили представление о
строении материи на масштабах <10-8см. Описание физических явлений,
происходящих на расстояниях меньше 10-8 см, взаимодействия атомов,
атомных ядер, фундаментальных частиц, требует принципиально нового
подхода. На этих масштабах проявляются квантовые свойства объектов,
которые не подчиняются законам классической физики. Явления
микромира описываются на основе законов квантовой физики.
Дискретный характер состояний, характеризующих атомные и ядерные
системы, противоречит основному положению классической физики –
бесконечно малое изменение силы вызывает бесконечно малое изменение
состояния
системы.
Описания состояний в классической и квантовой физике существенно
различаются. В классической физике состояние материальной точки в
любой заданный момент времени t полностью описывается заданием её
координат и импульса. Зная эти величины в момент времени t, можно
определить динамику материальной точки под действием известных сил во
все последующие и предыдущие моменты времени. В квантовой физике
процессы имеют вероятностный характер и описываются с помощью
волновой функции. Волновая функция позволяет определить средние
значения физических величин, характеризующих систему. В квантовой
физике каждой физической величине классической физики соответствует
квантовый оператор
импульса имеют вид
. В частности операторы проекции
80
Действие операторов проекции импульса на волновую функцию сводится
к вычислению производной от волновой функции. Операторы координат
совпадают с классическими численными выражениями, т.е. являются
числами.
Квантовая механика – теория, описывающая квантовые частицы,
движущиеся со скоростью много меньшей скорости света с. Связь между
операторами в квантовой механике имеет тот же вид, что и в классической
физике. Так полной энергии частицы E, состоящей из кинетической Tкин и
потенциальной Uпот энергий,
в квантовой физике соответствует оператор полной энергии
Гамильтона)
(оператор
Временная эволюция системы в квантовой физике в нерелятивистском
случае описывается уравнением Шредингера
являющимся аналогом уравнения Ньютона в классической физике. Если
потенциал U не зависит от времени t U = U(x,y,z), то решение уравнения
Шредингера имеет вид
где E – полная энергия квантовой системы, а волновая функция
ψ(x,y,z) удовлетворяет стационарному уравнению Шредингера
Наряду с такими привычными из классической физики величинами как
энергия, импульс в квантовой физике появляются величины, не имеющие
аналогов в классической физике. Одной из таких величин является спин –
собственный механический момент частицы. Понятие спина было введено
81
в квантовую физику в 1925 г. Дж. Уленбеком и С. Гаудсмитом на основе
анализа спектров атомов. Для правильного писания наблюдаемых спектров
атомов электрону было необходимо приписать ещё одно квантовое число
s.
Квантовое
число
спина
электрона
s=
1/2.
Волновая функция частицы со спином зависит не только от её трех
пространственных координат и времени, но и от спина, характеризующего
внутреннее состояние частицы. Так же как и в случае полного момента
количества движения одновременно можно измерить только квадрат
полного спина и одну из его проекций на произвольную ось. Две проекции
на разные оси одновременно не имеют определенные значения. Обычно в
качестве проекции спина выбирают проекцию на ось z, определяемую
условиями проведения измерений. В отличие от пространственных
координат спиновая переменная может принимать лишь дискретные
значения. Для частицы, имеющей значение квантового числа спин s = 1/2
проекция спина sz может принимать два значения sz = ±1/2. Поэтому
волновую функцию ψ(x,y,z,t,sz) обычно записывают в виде столбца,
имеющего две строки
При s = 1/2 матрицы квадрата полного спина
проекции на ось z имеют вид
Матрицы
x
и
y
и его
в этом представлении имеют вид
.
Матрицы
x,
y,
z
называются матрицами Паули.
Де Бройль выдвинул теорию, в которой устанавливалась связь между
частицами и волнами. Это была очень стройная теория и она сразу
привлекла меня своей красотой. Частицы и волны были связаны
релятивистским образом, причем так, что при стремлении масс покоя
частиц к нулю, получалось соотношение между квантами света и
электромагнитными волнами. Восхищенный красотой работы де Бройля, я,
тем не менее, не мог воспринимать волны всерьез. Я всецело пребывал во
власти теории Бора и предложенные им орбиты понимал совершенно
буквально – электроны были реально существующими частицами, а волны
де Бройля представлялись мне просто математической выдумкой,
82
совершенно не существенной для физиков. Моя точка зрения была,
конечно, совершенно неправильной. Работу де Бройля прочитал
Шрёдингер. У Шрёдингера был иной подход и он получил другое
образование. Он хорошо изучил собственные функции и собственные
векторы, о которых я не знал совсем ничего. Поэтому Шрёдингер со своим
взглядом на мир сумел развить идеи де Бройля и получить блестящий
результат. Примитивные формулы де Бройля, которые годились только для
описания свободных частиц, Шрёдингер распространил на частицы,
движущиеся в электромагнитном поле, что привело его к волновой
механике.
П. А. М. Дирак. «Воспоминания о необычной эпохе»
Нобелевская премия по физике
1933 г. – Э Шредингер и П. Дирак. За открытие новых плодотворных
формулировок атомной теории
2. Уравнение Дирака
Уравнение Шредингера
применимо для описания частиц, скорость которых меньше скорости света
c. Оно не удовлетворяет принципам специальной теории относительности,
т.к. не инвариантно относительно преобразований Лоренца. В уравнение
Шредингера координаты и время входят неравноправно – оно содержит
первую производную по времени и вторые производные по координатам.
Релятивистская механика основана на соотношении
E2 =
2.1
c2p2 +
m2c4,
связывающем энергию и импульс частицы. Для получения
релятивистского уравнения можно поступить так же, как в
нерелятивистском случае уравнения Шредингера. Для получения
волнового уравнения в соотношении (2.1) от классических величин
энергии E и импульса p нужно перейти, так же как в уравнении
Шредингера, к операторам
83
и подействовать на волновую функцию ψ.
Релятивистское волновое
уравнение было получено независимо Клейном, Гордоном и Фоком и
носит их имя
Состояние частицы зависит от трёх координат и времени ψ(x,y,z,t).
Уравнение Клейна–Гордона–Фока представляет собой волновое уравнение
второго порядка. Оно описывает динамику релятивистской квантовой
системы. Так как уравнение Клейна–Гордона–Фока является уравнением
второго порядка, для его решения в начальный момент времени
необходимо задать значение не только волновой функции ψ, но и её первой
производной. Оказалось, что для уравнения Клейна–Гордона–Фока нельзя
ввести положительно определённую плотность вероятности ψ*ψ.
Уравнение Клейна–Гордона–Фока описывает состояние частиц с нулевым
значением спина. Однако уже к тому времени, когда П. Дирак работал над
релятивистской теорией электрона (1925 г.), было известно, что электрон
имеет спин s = 1/2. Спин электрона был введён в 1925 г. Дж. Уленбеком и
С. Гоудсмитом для объяснения дублетной структуры одноэлектронных
уровней.
Принцип суперпозиции требует, чтобы релятивистское
волновое уравнение было линейным. На основании этих принципов
П. Дирак сформулировал релятивистски-инвариантное уравнение, записав
его в виде
2.2
Соотношение представляет собой наиболее общую линейную форму,
содержащую первые производные от волновой функции ψ. В уравнение
(2.2) координаты и время входят равноправно и не содержат вторых
производных. Для нахождения величин αx, αy, αz, β уравнение (2.2) можно
записать в виде
2.3
где
84
имеющем формальное сходство с уравнением Шредингера. Если
оператор представляет собой оператор Гамильтона, то между
оператором и операторами импульса должна быть такая же связь как
между энергией и импульсом в специальной теории относительности
2.4
Используя соотношение (2.4), можно
коэффициенты αx, αy, αz, β. Возведя оператор
определить неизвестные
в квадрат, получим
Оператор 2 будет иметь вид (2.4), если величины αx, αy, αz, β будут
удовлетворять следующим условиям.
+αkαi =0, α≠k,αiβ=βαi =0,
i = x,y,z.
Очевидно, что обычные числа не могут удовлетворять условиям (2.5), т.к.
для них не выполняются условия антикоммутации. Для обычных чисел
выполняются условия коммутации αiαk + αkαi = 0. Дирак предположил, что
условиям коммутации (2.5) удовлетворяют матрицы 4 порядка,
составленные из матриц Паули.
85
2.6
Умножая матрицы (2.6) друг на друга можно убедиться, что они
удовлетворяют условиям (2.5).
Используя матрицы Паули σx, σy, σz,
матрицы αx, αy, αz, β можно записать в виде
С помощью операторов
x,
y,
z,
уравнение (2.2) приводится к виду
Это уравнение называется уравнение Дирака для свободной частицы.
Если ввести векторный оператор
можно записать в более компактном виде
, то уравнение Дирака
Так как на волновую функцию ψ(x,y,z,t) действуют матрицы 4×4,
волновая функция ψ(x,y,z,t) также должна быть четырехкомпонентной.
Матричное волновое уравнение Дирака эквивалентно системе четырех
связанных между собой уравнений
86
Четырехкомпонентную волновую функцию электрона можно
представить как 4 различных комбинации положительной и отрицательной
энергий электрона и двух значений проекции спина электрона σz = 1/2 и
σz = -1/2.
П. Дирак: «Коль скоро я взялся оценивать других физиков, нельзя не
сказать о Шрёдингере. Мне кажется, что я никогда не видел его в
Копенгагене, во всяком случае, я этого не припомню. Но мы немало
встречались потом, и из всех знакомых физиков Шрёдингер был, наверное,
больше других похож на меня. Я обнаружил, что с Шрёдингером я
соглашался гораздо легче, чем с кем-нибудь другим. Дело, наверное, было
в том, что мы оба очень ценили математическую красоту и воплощение
этой красоты в нашей работе. Для нас было символом веры то, что все
уравнения, описывающие фундаментальные законы Природы, должны
отличаться математической красотой. Это было для нас почти религией,
причем очень полезной, ибо ее можно считать основой многих наших
успехов.
Когда вы читаете о работах Шрёдингера. вас может удивить
одно обстоятельство. Шрёдингер пришел к квантовой механике через
волновое уравнение де Бройля, которое было релятивистским. Шрёдингер
находился под большим впечатлением красоты релятивистской теории
относительности, и возникает вопрос, почему так случилось, что работа
Шрёдингера, где он вводит волновое уравнение, написана в
нерелятивистском духе. Здесь кроется какое-то противоречие.
Много лет спустя, не помню точно, но примерно году в 1940-м, близко
познакомившись с Шрёдингером, я узнал от него, в чем было дело. Он
рассказал, что работал тогда в релятивистском подходе, навеянном
работами де Бройля, и, вводя электромагнитные потенциалы, пришел к
релятивистскому волновому уравнению, которое оказалось обобщением
уравнения де Бройля. Первый его порыв быт посмотреть, что получится,
если с помощью этого уравнения рассчитать атом водорода.
Произведя расчеты, Шрёдингер обнаружил, что результаты не согласуются
с
опытом.
87
Он был сильно разочарован и, решив, что его волновое уравнение
никуда не годится, отказался от него. Взглянув на это уравнение поновому через несколько месяцев, Шрёдингер заметил, что если понизить
точность и перейти к нерелятивистскому приближению, то результаты
согласуются с экспериментальными данными, конечно, в пренебрежении
релятивистскими эффектами. Таким образом, волновое уравнение
Шрёдингера в нерелятивистском виде согласовывалось с экспериментом, и
его можно было публиковать.
Причиной того, что первоначальное,
релятивистское уравнение Шрёдингера не согласовывалось с
экспериментом, был, конечно, неучтенный спин электрона. Мысль о том,
что у электрона есть спин, была тогда совершенно новой, и Шрёдингер мог
о ней даже не слышать, а в то время у него не хватало смелости
публиковать уравнение, которое давало результат, наверняка
противоречащий эксперименту[*]».
Решение уравнения Дирака для свободной частицы показывает, что
каждому значению импульса p соответствуют два значение энергии E
E = ±(m2c4 + c2p2)1/2,
т.е. энергия частицы может принимать два значения, как
положительное, так и отрицательное. В классической физике все величины
изменяются непрерывно, поэтому без потери общности отрицательные
значения энергии можно было отбросить, т.к. положительные и
отрицательные области энергии разделены энергетическим интервалом
2mc2 и непрерывный переход частицы из одной области в другую
невозможен. Однако в релятивистской квантовой теории возможны
квантовые переходы из состояний с отрицательной энергией в состояния с
положительной энергией и обратно. Поэтому отрицательные значения
энергии отбросить нельзя. Возникла проблема − как интерпретировать
состояния электрона с отрицательной энергией? Какой физический смысл
имеют состояния с отрицательной энергией? Рассмотрим ситуацию, когда
частица с положительной энергией E0 > 0 переходит из точки А в точку В.
Тогда в точке А величина энергии E уменьшается на величину E0, а в точке
В увеличивается на величину E0. Для частицы с отрицательной энергией
E0 < 0 переход их точки А в точку В приводит к увеличению энергии на
величину E0 в точке А и уменьшению энергии на величину E0 в точке В.
Таким образом, переход частицы с отрицательной энергией из точки А в
точку В равнозначен переходу частицы с положительной энергией их
точки В в точку А. То есть процессы с отрицательной энергией можно
88
представить как процессы с положительной энергией, но обращенные во
времени. Частица с отрицательной энергией ведет себя, как частица с
положительной энергией, но движущаяся по времени в обратном
направлении по сравнению с частицей с положительной энергией.
Рассмотренный пример относился к нейтральным частицам, не имеющим
электрического заряда. Рассмотрим теперь ситуацию с заряженной
частицей, совершающей переход из точки А в точку В.
В случае положительного заряда частицы q, заряд в точке А уменьшается
на величину -q, а в точке В увеличивается на величину +q. Поэтому для
сохранения симметрии мы должны при переходе частицы с отрицательной
энергией одновременно изменить знак электрического заряда на
противоположный.
Переход частицы с положительной энергией E и зарядом +q из
состояния А в В равнозначен переходу частицы с отрицательной
энергией -E и зарядом -q из состояния В в состояние А. Состояния с
отрицательной энергией приводят к появлению у каждой частицы
двойника,
который
имеет
положительную
энергию
и
противоположный электрический заряд.
Таким образом, согласно
теории Дирака, заряженная частицы должна иметь двойника с
противоположным зарядом и такой же массой. Например, у электрона
должен быть двойник, имеющий такую же массу, как электрон, но
положительный электрический заряд.
На «языке» квантовой физики волновую функцию частицы с
положительной энергией E+ = E > 0, движущейся в положительном
направлении вдоль оси х, записывают в виде
В случае постоянной фазы волны
т.е. частица с положительной энергией движется вправо вдоль оси x. Для
состояния с отрицательной энергией E- (E < 0) волновая функция имеет
вид
89
В этом случае условие постоянной фазы приводит к соотношению
т.е. частица с отрицательной энергией движется вдоль оси x в
отрицательном направлении, имея положительную энергию |E-|.
Частица с отрицательной энергией ведёт себя, как частица с
положительной энергией, но движущаяся «назад по времени». Другой
пример движения «назад по времени» − поведение частицы с
отрицательным зарядом -q, движущейся в постоянном магнитном поле.
Движение частицы описывается уравнением Лоренца
т.е. движение частицы с положительным зарядом +q описывается тем же
уравнением, что и частицы с отрицательным зарядом. Но частица с
положительным зарядом в этом случае движется назад по времени −
вращается в противоположном направлении в магнитном поле.
Из рассмотренных примеров видно, что частица, имеющая
электрический заряд +q и отрицательную энергию, ведёт себя так же как и
частица с отрицательным электрическим зарядом -q и положительной
энергией.
Электрон с отрицательной энергией должен двигаться во внешнем поле
как частица с положительным зарядом. Поэтому при переходе электрона
области положительных энергий в область отрицательных энергий должен
одновременно измениться заряд электрона – он должен стать
положительным +e. Переходы электронов в состояния с отрицательной
энергией нарушали закон сохранения электрического заряда. Нужно было
найти способ запретить такие переходы. Ход мыслей П. Дирака был
следующий. Так как электроны являются фермионами, это можно было
сделать, предположив, что все состояния с отрицательной энергией заняты.
Тогда в соответствии с принципом Паули переходы в состояния с
отрицательной энергией оказываются запрещёнными. Однако такое
предположение приводило к новой проблеме − бесконечному числу
частиц, заполняющих все отрицательные состояния − появлению
физического вакуума, имеющего бесконечный электрический заряд и
массу. Возможность такого состояния Дирак объяснил тем, что
бесконечный физический вакуум будет ненаблюдаем, так как наблюдаются
только отклонения энергии или электрического заряда от состояния
физического вакуума. Можно ли обнаружить электроны заполняющие
90
отрицательные состояния физического вакуума? Гамма-квант с энергией
большей, чем 2mec2 может перевести электрон из состояния с
отрицательной энергией в состояние с положительной энергией. Тогда
будет наблюдаться обычный электрон с положительной энергией и
отрицательным зарядом, а вакантное место в вакууме будет наблюдаться
как частица с положительным зарядом. Так как в то время была известна
всего одна частица с положительным электрическим зарядом – протон,
Дирак первоначально отождествил протоны с частицами, заполняющими
отрицательные состояния вакуума. Однако это предположение породило
новые, гораздо более сложные проблемы − неустойчивость нашего мира −
приводило к невозможности существования атома водорода. Электрон и
протон должны были в результате взаимодействия исчезнуть,
превратившись в γ-кванты. Кроме того, необходимо было объяснить
большую разницу масса электрона и протона. Если протон это
действительно дырка, образовавшаяся в результате вылета электрона,
почему протон имеет массу в 2000 раз больше массы электрона? Дирак
верил в созданную им теорию дырок и в результате сделал следующий
шаг. Он объявил, что должна существовать новая неизвестная частица,
имеющая такую же массу как электрон, но положительный электрический
заряд. Эта частица является античастицей по отношению к электрону.
П. Дирак: «На протяжении двух лет я занимался боровскими орбитами и
пришел к выводу, что развить их в общую квантовую механику
безнадежно. В это время Гейзенберг предложил свою матричную
механику, и мне вдруг стало ясно, что ключом к решению проблемы
служит некоммутативная алгебра. Вскоре Шредингер разработал
волновую механику и показал, что она эквивалентна теории Гейзенберга.
Основываясь на этих теориях, я развил общую теорию преобразований,
которую можно было применять при вычислении вероятностей любых
коммутирующих динамических переменных. Это доставило мне большое
удовлетворение.
Для построения релятивистской теории частицы имелось волновое
уравнение Клейна − Гордона, квадратичное по ∂/∂t. В то время оно
удовлетворяло большинство физиков. Мне же оно не нравилось, потому
что я был очень привязан к своей теории преобразований, которая
91
требовала,
чтобы
уравнение
было
линейным
по ∂/∂t.
Эта
неудовлетворенность заставила меня продолжить поиски нового
релятивистского волнового уравнения. Наконец, я нашел уравнение,
линейное по ∂/∂t и совместимое с моей теорией преобразований. Оно
автоматически привело к спину h/2 и к правильному значению магнитного
момента электрона. Эти результаты были неожиданными для меня.
Я применил это уравнение к электрону в атоме водорода в первом
приближении теории возмущений и получил результаты, согласующиеся с
данными опыта. Уравнение автоматически приводило к правильному
магнитному .моменту, и именно поэтому оно не содержало той ошибки,
которая получалась при использовании уравнения Клейна − Гордона,
приводившего к неверным результатам для спектра водорода.
Но у этого уравнения имелась и новая трудность, а именно, частица
могла находиться в состояниях с отрицательной энергией. Я знал о такой
трудности с проблемой отрицательных энергий с самого начала работы, но
считал это затруднение менее серьезным по сравнению с остальными, не
столь
серьезным,
как,
например,
невозможность
применять
преобразования, вытекающие из общей теории преобразований.
Проблема отрицательных энергий была разрешена несколько позже
выдвинутой мною идеей об учете принципа исключения Паули для
электронов (согласно которому в любом данном состоянии не может
находиться более одного электрона) при дополнительном смелом
предположении, что все состояния с отрицательной энергией в вакууме
заполнены, а потому дырка в состояниях с отрицательной энергией
проявляется как физическая частица. Это была бы частица со спином
электрона, но она обладала бы положительным зарядом вместо
отрицательного заряда у электрона и имела бы положительную энергию.
Когда я впервые обдумывал эту идею, я считал, что новая частица
должна иметь такую же массу, что и электрон, вследствие симметрии
между положительными и отрицательными массами и энергиями, которая
всюду проявляется в теории. Но в те времена единственными известными
элементарными частицами были электрон и протон. Я не осмелился
постулировать существование новой частицы. Весь климат общественного
мнения в те дни был против постулирования новых частиц, в резком
контрасте с тем, что мы наблюдаем сейчас. Тогда я опубликовал свою
работу как теорию электронов и протонов в надежде, что каким-то
необъяснимым образом кулоновское взаимодействие между частицами
приведет к большому отличию в массах электрона и протона.
Конечно,
в этом пункте я был совершенно неправ и вскоре математики указали, что
абсолютно невозможно получить такую асимметрию между состояниями с
положительной и отрицательной энергиями. И впервые Вейль опубликовал
категорическое утверждение о том, что новая частица должна иметь такую
же массу, что и электрон. Теория с равными массами была подтверждена
немного спустя на опыте, когда Андерсон обнаружил позитрон».
92
Частица с зарядом +q является античастицей по отношению к частице с
зарядом -q. Аналогичные рассуждения относятся к частице с
отрицательным зарядом. Частицы с отрицательной энергией являются
античастицами по отношению к частицам с положительной энергией.
Наряду с электроном, имеющим отрицательный электрический заряд,
должна, согласно уравнению Дирака, существовать положительно
заряженная античастица. Античастицы должны существовать не только
у электрически заряженных частиц, но и у частиц, имеющих
сохраняющуюся в различных физических процессах физическую
величину. Одним из таких квантовых чисел является барионное число
(заряд) B. Поэтому нейтрон, имеющий электрический заряд Q = 0, но
единичный положительный барионный заряд, тоже должен иметь
античастицу – антинейтрон.
B(n) = +1, Q(n) = 0; B( ) = -1, Q( ) = 0
Античастицей протона является частица, имеющая такую же массу как
протон, равный по абсолютной величине, но отрицательный
электрический заряд. Барионные заряды протона и антипротона также
имеют противоположные значения
B(p) = +1, Q(p) = +1e; B( ) = -1, Q( ) = -1e
С современной точки зрения в большинстве случаев нет необходимости
рассматривать античастицы как частицы, распространяющиеся назад во
времени. Гораздо проще рассматривать частицы и античастицы как
физические объекты, характеризующиеся определённым набором
квантовых чисел. Какие-то квантовые числа у частицы и античастицы
совпадают, а какие-то имеют противоположные значения. Существенно то,
что

частица и античастица при взаимодействии аннигилируют,

из состояния с нулевыми квантовыми числами частица и античастица
всегда рождаются парами.
Поэтому в дальнейшем на диаграммах Фейнмана мы не будем рисовать
стрелки, а рядом с внешними и внутренними линиями в тех случаях, когда
это необходимо, будем указывать тип частицы.
[*] Dirас P. А. М. Recollections of an Exciting Era//History of Twentieth
Century Physics: Proceedings of the International [Summer] School of Physics
«Enrico Fermi». Course LVII. Varenna, Lake Como, Italy, villa Monastero. July
93
31 - August 12. 1972,- (Rendiconti S. I. F. - LVII).- New York: Academic Press,
1977 - P. 109-146.- УФН, том 153, вып. 1 (1987). Перевод
H. Я. Смородинской.
4. Электромагнитные взаимодействия
Электромагнитное взаимодействие является одним из четырех типов
фундаментальных взаимодействий:

сильное взаимодействие,

электромагнитное взаимодействие,

слабое взаимодействие,

гравитационное взаимодействие.
Переносчиком электромагнитного взаимодействия является квант
электромагнитного поля – фотон. Радиус действия сил R и масса
переносчика взаимодействия m связаны соотношением
R = ћ/mc.
Так как фотон имеет нулевую массу, радиус действия электромагнитных
сил
бесконечный.
Поэтому
к
электромагнитному
взаимодействию
сводится большинство явлений, наблюдаемых в макроскопических
масштабах – силы трения, упругости и другие. Безразмерная константа
α =e2/ћc = 1/137
определяет интенсивность электромагнитного взаимодействия.
Фундаментальная вершина электромагнитного взаимодействия
Процессы квантовой электродинамики описываются с помощью одной
фундаментальной вершины состоящей из двух фермионных линий ƒ и
одной фотонной γ (рис. 4.1)
94
Рис. 4.1. Фундаментальная вершина, описывающая виртуальный процесс
испускания фермионом (электроном) фотона.
Вершина электромагнитного взаимодействия описывает виртуальный
процесс испускания фермионом, например, электроном фотона (рис. 4.1).
Этот процесс является виртуальным, т.к. свободный электрон ни
испустить, ни поглотить фотон не может, что можно показать,
воспользовавшись равноправием инерциальный систем координат и
рассмотрев процесс в системе координат, в которой электрон покоится
после поглощения фотона (рис. 4.2). Из законов сохранения энергии и
импульса следует
=
, т. к. до поглощения импульс фотона
равен
импульсу фотона
. После поглощения фотона электроном из закона
сохранения энергии следует
(c2p2 + m2c4)1/2 + |k|c = mc2.
Рис. 4.2. Виртуальный процесс поглощения электроном фотона.
Законы сохранения энергии и импульса могут может выполняться
только в том случае, если p = k = 0, т.е. в случае отсутствия фотона. В
зависимости от ориентаций фермионных и фотонных линий относительно
оси времени основной узел квантовой электродинамики описывает
95
различные виртуальные процессы взаимодействия электронов, позитронов
и
фотонов.
В приведенных ниже виртуальных процессах (рис. 4.3–4.9) ось времени
направлена слева направо.
Рис.4.3. Виртуальный процесс испускания электроном фотона
Рис. 4.4. Виртуальный процесс испускания фотона позитроном. Позитрон
распространяется по оси времени в противоположном направлении.
Рис. 4.5. Виртуальные процессы поглощения фотона электроном (слева)
позитроном (справа).
96
Рис. 4.6. Виртуальные процессы e+e--аннигиляции (слева), образования
пары электрон-позитрон (справа).
Образование e+e--пар
Релятивистское обобщение Дираком теории электрона привело не
только к предсказанию позитрона, но и к предсказанию того, что при
достаточно высоких энергиях E > 1 МэВ возможен процесс образования
электрон-позитронных
обнаружен
пар.
Этот
процесс
в
был
экспериментально
1932
г.
Во всех процессах, происходящих в Природе, выполняется закон
сохранения
электрического
заряда.
Электрону
приписывается
электрический заряд Q = -1, протону − Q = +1, фотону и другим
нейтральным частицам приписывается величины электрического заряда
Q = 0. Позитрон, являющийся античастицей по отношению к электрону
имеет электрический заряд Q = -1.
Закон сохранения электрического заряда
Квантовое число суммарного электрического заряда не изменяется во всех
типах взаимодействий. Сумма всех квантовых чисел электрического
заряда частиц после взаимодействия равна их сумме до взаимодействия.
97
Закон сохранения электрического заряда не запрещает изменение числа
заряженных частиц. В результате аннигиляции электрона и позитрона
число заряженных частиц уменьшается на две единицы. При этом
суммарный
электрический
заряд
остаётся
равным
нулю,
как
до
взаимодействия, так и после взаимодействия. Процесс рождения электронпозитронной пары подчиняется тому же закону сохранения электрического
заряда. Любая частица может быть рождена или уничтожена одновременно
со
своей
античастицей.
При
этом
автоматически
все
квантовые
числа
будут
сохраняться.
Из законов сохранения импульса и энергии следует, что процесс
образования электрон-позитронных пар не может происходить в вакууме.
Процесс образования пар происходит лишь в кулоновском поле третьей
частицы, получающей часть импульса и энергии. Процесс рождения
фотоном электрон-позитронной пары в поле атомного ядра Z показан на
рис. 4.7.
Рис. 4.7. Образование e+e--пары в кулоновском поле атомного ядра.
В более компактном виде диаграмму Фейнмана образования электронпозитронной пары в кулоновском поле атомного ядра можно изобразить в
виде, показанном на рис. 4.8.
98
Рис. 4.8. Образование e+e--пары в кулоновском поле атомного ядра.
Диаграмма Фейнмана рассеяния фотона на фотоне имеет вид.
Рис. 4.9. Диаграмма Фейнмана рассеяния фотона на фотоне.
Образование e+e--пар в поле атомного ядра происходит в случае, если
энергия γ-кванта удовлетворяет соотношению
Eγ ≥ 2mec2 + En,
где первый член соответствует энергии покоя пары электрон и позитрон, а
второй − энергии отдачи ядра. Так как энергия отдачи ядра сравнительно
мала, то энергия, определяемая первым членом, является порогом
рождения пар (2mec2
1.022 МэВ). Одиночный квант любой энергии не
может превратиться в электрон-позитронную пару, т.к. при этом не
выполняются одновременно законы сохранения энергии и импульса. В
основном образование e+e--пар происходит в кулоновском поле ядер
атомов. Эффективное сечение этого процесса пропорционально квадрату
заряда ядра Z2. Электрон-позитронные пары также могут образовываться в
кулоновском
поле
электрона.
В этом случае порог рождения e+e--пар в поле электрона равен 4mec2.
Увеличение порога рождения e+e--пар в кулоновском поле электрона
99
связано с тем, что энергию отдачи получает электрон, имеющий малую
массу, и пренебречь ею уже нельзя. Образование пар в поле электрона
имеет сравнительно малую вероятность. На рис. 4.10 показана зависимость
сечений образования e+e--пар на протоне и электроне в области энергий до
100 МэВ. С увеличением энергии γ-кванта разность сечений убывает.
Рис. 4.10. Эффективные сечения образования электронно-позитронных пар
γ-квантами с энергией ≤100 МэВ на протоне и электроне.
На рис. 4.11 приведено теоретически рассчитанное эффективное сечение
образования электронно-позитронных пар γ-квантами на протоне, атомах
водорода и свинца в области энергий до 106 МэВ.
100
Рис. 4.11. Эффективное сечение образования электронно-позитронных пар
γ-квантами большой энергии на протоне σp и атомах водорода σH и свинца
σPb.
На рис. 4.12 показана вероятность P образования фотоном e+e--пар в
веществе с различным зарядом ядер. Видно, что вероятность образования
электрон-позитронной
пары
растет
с
ростом
энергии
фотона
и
увеличением заряда ядра и достигает предельного значения в области
нескольких сотен МэВ.
Энергия γ-кванта (МэВ)
101
Рис. 4.12. Зависимость вероятности образования электрон-позитронной
пары в кулоновском поле атомного ядра от заряда атомного ядра и энергии
фотона.
При образовании e+e--пары часть энергии γ-кванта E превращается в
энергию
покоя
пары
частиц
2mec2,
а
оставшаяся
энергия
E − 2mec2 переходит в кинетические энергии трех частиц: электрона e-,
позитрона e+ и атомного ядра (или электрона), в поле которого происходит
образование пары. Распределение кинетической энергии между этими
тремя частицами зависит от масс частиц и углов их разлёта. Поэтому
энергия частиц не определяется однозначно направлением вылета частиц,
а имеет непрерывное распределение от нулевой до максимальной
E − 2mec2.
Максимальная
энергия
позитрона
или
электрона
при
образовании пар на атомных ядрах близка к энергии E − 2mec2, т. к. масса
ядра велика по сравнению с массами электрона и позитрона me, а энергия
отдачи
ядра
мала.
На рис. 4.13 показаны теоретически рассчитанные спектры электронов
(позитронов) при образовании e+e--пар γ-квантами различных энергий.
Угловое распределение позитронов и электронов зависит от энергии γкванта E. Если E >> 2mec2 импульс образовавшейся e+e--пары близок по
величине и направлению к импульсу γ-кванта, т.е. электрон и позитрон
летят в том же направлении, что и образовавший их γ-квант, с малым
относительным углом разлёта электрона и позитрона. Средний угол вылета
частиц θ имеет величину
θ ≈ mec2/E.
102
Рис. 4.13. Теоретически рассчитанные спектры позитронов (электронов)
при образовании пар γ-квантами различной энергии E/mec2 в воздухе.
В
природных
условиях
образование
e+e--пар
происходит
при
взаимодействии космических лучей с веществом. Распады положительно и
отрицательно заряженных мюонов
μ- →
μ+ → e+ + νe +
e- +
e
+
νμ,
μ,
составляющие сильно проникающую компоненту космического излучения,
и распады π0-мезонов
π0 → 2γ
приводят к образованию каскадных ливней и размножению числа e +e--пар.
Образование e+e--пар эффективно происходит в звездах, когда
температура повышается выше 109К. Взаимодействие электронов и
позитронов с атомными ядрами приводит к образованию химических
103
элементов в звездах и, в частности, к образованию химических элементов в
районе железного максимума. Образование и последующая аннигиляция
e+e--пар
γ → e+e- → ν
имеют большое значение в механизме испускания нейтрино в звездах и
влияют на эволюцию звезд. Аннигиляция электрон-позитронных пар с
образованием пары ν приводит к заметной потере энергии в звездах.
e+e--аннигиляция. Низкие энергии
Одним из ярких свойств взаимодействия частиц и античастиц является
процесс аннигиляции. Аннигиляция − это процесс, в котором частица и
соответствующая
ей
античастица
превращаются
в
кванты
электромагнитного поля или в другие частицы − кванты физических полей
другой природы. Характер продуктов аннигиляции и соотношение
вероятностей различных каналов аннигиляции определяются типом
взаимодействия и правилами отбора, вытекающими из закона сохранения.
Например, при соударении электрона и позитрона они оба могут
исчезнуть, образовав два фотона:
e+ + e- → 2γ.
При достаточно высокой энергии электрон-позитронная пара может
превратиться в совокупность тяжелых частиц − адронов, например,
возможен процесс образования пары протон–антипротон
e+ + e- → p + .
Для того чтобы была возможна аннигиляция пары e+e- с образованием
протона и антипротона, полная суммарная энергии пары электрон–
позитрон в системе центра масс должна быть больше, чем суммарная
104
масса
протона
и
антипротона,
т.
е.
больше
(2×940)
МэВ.
Процесс аннигиляции при низких энергиях E < mμc2 ниже порога
рождения наиболее лёгких заряженных лептонов μ+μ--мюонов приводит к
единственному процессу − рождению γ-квантов. Основным процессом при
этих
энергиях
будет
двухфотонная
аннигиляция.
Попав в вещество, позитрон испытывает большое количество
столкновений с атомами вещества и быстро теряет энергию на их
ионизацию.
Сечение
двухфотонной
аннигиляции
для
свободного
электрона и позитрона, движущихся с относительной скоростью v << c,
вычисленное Дираком, описывается следующей зависимостью от скорости
позитрона v:
где r0 − классический радиус электрона, а скорость v выражена в см/с.
Вероятность аннигиляции позитрона λ небольшой энергии в среде с
плотностью электронов Ne определяется соотношением
λ = Neσv = Neπr02c = 0.7·10-14

Время жизни позитрона τ в конденсированной среде Ne = 1024 см–3
τ = 10-10 с.

В межзвездной среде Ne = 1 см–3 время жизни медленного позитрона
относительно аннигиляции
τ = 1014 с ≈ 3·106 лет.
Сечение аннигиляции быстро падает с увеличением относительной
скорости сталкивающихся частиц. Поэтому в подавляющем большинстве
случаев аннигиляция происходит после того, как позитрон потеряет всю
свою
энергию
на
ионизацию,
т.
105
е.
при
v ≈ 0.
Следовательно,
относительный
момент
происходить
e+e--пары l = 0 и
в
e+e--аннигиляция
будет
S-состоянии.
Рассмотрим, как влияют законы сохранения на процесс двухфотонной
аннигиляции остановившегося позитрона. Из закона сохранения энергии
следует
m+c2 + m-c2 = Eγ1 + Eγ2,
где m+, m- − масса соответственно позитрона и электрона (m+c2 + m-c2 =
0.511 МэВ), Eγ12 − энергии образовавшихся фотонов. Из закона сохранения
импульса следует
0 = P+ + P- = Pγ1 + Pγ2.
Выполнение законов сохранения энергии и импульса приводит к тому, что
рождающиеся в двухфотонной аннигиляции γ-кванты имеют одинаковые
энергии:
Eγ1 = Eγ2 = mec2
и
разлетаются
в
противоположных
направлениях.
В том случае, когда аннигилирует движущийся позитрон (v ≠ 0), угол
разлета фотонов и распределение энергии между фотонами зависят от
скорости позитрона. При больших энергиях ε аннигилирующих
позитронов (ε >> mec2) фотоны испускаются преимущественно вперед и
назад относительно направления движения позитронов. Фотон, летящий
вперед, уносит почти всю энергию позитрона, на долю же фотона,
летящего назад, остается энергия, примерно равная половине энергии
покоя электрона mec2/2. На аннигиляции ускоренных пучков позитронов
основан метод получения квазимонохроматических γ-квантов высокой
энергии.
Векторная диаграмма импульсов фотонов в случае трехфотонной
аннигиляции показана на рис. 4.14.
106
Рис. 4.14. Векторная диаграмма импульсов фотонов в случае трёхфотонной
аннигиляции.
Суммарный момент J, уносимый фотонами в случае двухфотонной и
трехфотонной аннигиляции может иметь значение J = 0 или J = 1 в
зависимости от направлений спинов e+e--пары (рис. 4.15).
Рис. 4.15. Возможные значения полного спина J системы e+e- при
аннигиляции в S-состоянии.
107
Рис. 4.16. Процесс аннигиляции пары e+e-: а) двухфотонная аннигиляция;
б) трехфотонная аннигиляция.
Процесс
аннигиляции
пары
e+e- изображается
диаграммами,
показанными на рис. 4.16. Процесс двухфотонной аннигиляции показан на
рис. 4.16а. На рис. 4.16б показан процесс испускания трех фотонов. На
рисунке ось времени направлена слева направо. Каждой частице на
диаграмме Фейнмана соответствует определенная линия. Сплошные линии
описывают электрон и позитрон, волнистые − фотоны. Свободные концы
линий соответствуют невзаимодействующим частицам в начальном и
конечном состояниях. Взаимодействие частиц на диаграммах описывается
вершинами (точки 1, 2, 3 на рис. 4.16) и рассматривается как испускание и
поглощение различных виртуальных частиц. Виртуальным частицам
соответствуют внутренние линии, соединяющие вершины. На диаграмме
рис. 4.16а в точке 1 электрон превратился в фотон и виртуальную частицу,
которая затем в точке 2 поглощается позитроном. Вершине сопоставляется
константа связи, характеризующая интенсивность взаимодействия. В
случае электромагнитных взаимодействий константа равна
108
α1/2 = (e2/ћc)1/2.
Амплитуда процесса пропорциональна константе связи в степени равной
числу вершин в диаграмме Фейнмана. Диаграмме с N вершинами
соответствует амплитуда A, пропорциональная αN/2. Эффективное сечение
процесса определяется квадратом амплитуды. Оно будет, таким образом,
пропорционально αN. Так как для электромагнитного взаимодействия
α << 1 наибольший вклад дают диаграммы с минимальным числом
вершин. Поэтому, не проводя расчетов, можно оценить соотношение
вероятностей различных процессов. Так, например, для процессов,
изображенных на рис. 4.16, сечение двухфотонной аннигиляции примерно
на два порядка больше сечения трехфотонной аннигиляции
Таким
образом,
для
электромагнитных
процессов
каждая
дополнительная вершина соответствует подавлению процесса примерно на
2 порядка. Поэтому трехфотонная аннигиляция должна происходить
гораздо реже, чем двухфотонная. Эксперименты показывают, что из
каждой
тысячи
аннигилируют
Характерное
аннигилирующих
с
время
позитронов,
образованием
жизни
позитронов
лишь
трёх
в
веществе
единицы
фотонов.
~10–10c.
Если позитрон находится в веществе, в результате взаимодействия
позитрона с электронами и ядрами среды позитрон постепенно теряет
энергию до тех пор, пока его энергия не уменьшится настолько, что он
термализуется в среде. В результате взаимодействия с электроном среды
позитрон до того как произойдет e+e--аннигиляция может образовать
связанное состояние − позитроний. Поэтому аннигиляция часто идет через
образование связного состояния системы e+e--позитрония. Позитроний, в
котором спины электрона и позитрона антипараллельны (парапозитроний)
имеет время жизни 1.2·10-10 с и распадается на 2 γ-кванта. Позитроний, в
котором спины электрона и позитрона параллельны (ортопозитроний)
109
распадается на 3 γ-кванта и имеет среднее время жизни 1.4·10-7 с. Более
подробно см. п. 7 и 17.
Электромагнитные взаимодействия в e+e--соударениях
Исследование e+e--столкновений является эффективным средством
изучения электромагнитных взаимодействий лептонов. Электромагнитные
взаимодействия с участием лептонов при энергиях в системе центра масс
Eц.м. = 0.5 ГэВ представлены в основном следующими процессами:
1. e-e- → e-e-;
2. e+e- → γγ;
3. e+e- → e+e-;
4. e+e- → μ+μ-.
Реакции e-e- → e-e-, e+e- → e+e- и e+e- → γγ происходят во всём диапазоне
энергий Eц.м. сталкивающихся частиц. Рождение μ+μ--пар возможно при
энергии Eц.м. выше 214 МэВ (энергия покоя мюона mμc2 = 107 МэВ).
Дифференциальные сечения реакций при энергии Eц.м. = 1 ГэВ приведены
на рис. 4.17.
110
Рис. 4.17. Дифференциальные сечения реакций e-e- → e-e-, e+e- → e+e- и e+e→ γγ, e+e- → μ+μ- при Eц.м. = 1 ГэВ.
Характерной
особенностью
электромагнитных
взаимодействий
лептонов при высоких энергиях является сильная угловая зависимость
продуктов реакции от направления сталкивающихся частиц. Продукты
реакции вылетают в направлении сталкивающихся частиц. Большая часть
их вылетает в пределах угла θ ≈ mc2/E, где m − масса продуктов реакции,
E − энергия столкновения. Зависимость формы угловых распределений от
массы частиц в конечном состоянии отчетливо проявляется при сравнении
угловых распределений реакций e+e- → e+e- и e+e- → μ+μ-.
СПИНТРОНИКА – ЭЛЕКТРОНИКА НОВОГО ПОКОЛЕНИЯ
Достаточно молодая область современной физики – спиновая электроника, или спинтроника,
– притягивает всё больше исследователей многообещающими практическими
применениями. Если в традиционной электронике используется обычный электрический ток
(перемещаются заряды), то электроника нового поколения основана на ином физическом
принципе – в ней перемещаются спины электронов.
Спин электрона (собственный момент количества движения) – это внутренняя
характеристика электрона, имеющая квантовую природу и не зависящая от движения
электрона. Спин электрона может находиться в одном из двух состояний – либо «спинвверх» (направление спина совпадает с направлением намагниченности магнитного
материала), либо «спин-вниз» (спин и намагниченность разнонаправлены).
111
Обычно электроны в веществе в среднем неполяризованы – электронов со спином вверх и со
спином вниз примерно поровну. Орудием спинтроники является ток, создаваемый
электронами с однонаправленными спинами (спиновый ток). Для получения достаточно
сильного тока необходимо поляризовать спины, упорядочив их в одном направлении. Важно,
чтобы еще и время жизни спина (время, в течение которого направление спина не меняется)
было достаточно большим для передачи его на нужные расстояния.
Если традиционные электронные устройства, основанные на электрических свойствах
вещества, управляются преимущественно приложенным напряжением, то для манипуляции
спиновыми свойствами, характеризующимися направлением спина и временем его жизни,
необходимо использовать внешнее магнитное поле.
В чём секрет повышенного интереса к спинтронике? Во-первых, спиновые приборы будут
многофункциональны – они позволят совмещать на одном чипе функции накопителя для
хранения информации, детектора для ее считывания, логического анализатора для ее
обработки и коммутатора для последующей ее передачи к другим элементам чипа.
Во-вторых, такие устройства будут обладать высокой скоростью реагирования на
управляющий сигнал и потреблять значительно меньше энергии, чем устройства
традиционной электроники. Это объясняется тем, что переворот спина, в отличие от
перемещения заряда, практически не требует затрат энергии, а в промежутках между
операциями спинтронное устройство отключается от источника питания. При изменении
направления спина кинетическая энергия электрона не меняется, и значит, тепла почти не
выделяется. Скорость же изменения положения спина очень высока: эксперименты показали,
что переворот спина осуществляется за несколько пикосекунд (триллионных долей
секунды).
Эти преимущества позволят спинтронным устройствам стать основой для ЭВМ нового
поколения – квантовых компьютеров. Но чтобы это стало возможно, необходимо создать
ключевые элементы «спиновых микросхем» – спиновые транзисторы, то есть устройства, в
которых можно усиливать, ослаблять или выключать спиновый ток. А на базе спинового
транзистора уже будут создаваться новые компьютерные процессоры, сенсоры,
перепрограммируемые логические устройства и энергонезависимая быстродействующая
память высокой плотности.
СПИНОВОЙ ТРАНЗИСТОР: ТРУДНО СДЕЛАТЬ ПЕРВЫЙ ШАГ
В спиновом транзисторе состояния «включен» и «выключен» зависят от направления спинов
электронов, участвующих в токе. Любое спин-электронное устройство, в том числе и
спиновый транзистор, должно содержать три основных элемента:
1) механизм для электрического инжектирования (проще говоря «впрыска») спинполяризованных (то есть выстроенных в выбранном направлении) электронов в
полупроводник (будем называть этот механизм «инжектор»),
2) средства для управления спиновым током в полупроводнике (например, приложенное
напряжение, заставляющее двигаться электроны),
3) электрическая схема для прецизионного детектирования (измерения) результирующего
спинового тока (будем называть ее «детектор»).
Но наличия этих трех кирпичиков недостаточно, чтобы построить конечное устройство.
Нужно еще добиться высокой эффективности электрической инжекции спинов в
полупроводник и достаточной длины диффузии (перемещения) спина. А чтобы спин смог
преодолеть это расстояние в полупроводнике и достичь детектора, он должен обладать
достаточным временем жизни. И желательно, чтобы всё это происходило при комнатной
температуре (трудно себе представить домашний компьютер с процессором на базе
спиновых транзисторов, который работает только при охлаждении его до температуры
жидкого гелия!).
Человечество уже десять лет вкушает плоды спинтроники в виде компьютерных жестких
дисков и прецизионных сенсоров магнитного поля, в которых использован эффект
гигантского магнетосопротивления. Именно за открытие этого явления Альбер Фер и Петер
112
Грюнберг были удостоены Нобелевской премии по физике в этом году. Но создание
спинового транзистора и спиновой памяти до сих пор оставалось неразрешимой задачей. Все
предыдущие попытки с использованием дорогостоящих технологий и материалов (таких как
GaAs, ZnO, CdS) не увенчались успехом: получавшиеся спиновые транзисторы либо
работали только при очень низких температурах, либо работали при температурах, близких к
комнатной, но имели при этом очень малую величину эффективности, либо позволяли
передавать спиновый ток на очень незначительные расстояния, измеряемые сотнями
нанометров.
РЕВОЛЮЦИЯ В СПИНТРОНИКЕ СВЕРШИЛАСЬ
И вот настал момент, когда с уверенностью можно сказать, что создан первый в мире спинэлектронный транзистор, удовлетворяющий всем перечисленным выше критериям! Причем
он создан на базе кремния, которому пророчили позицию аутсайдера в современной
электронике.
Исследовательская группа в составе Иана Аппельбаума (Ian Appelbaum) и его аспиранта
Бициня Хуана (Biqin Huang) из Делавэрского университета (University of Delaware), а также
Доу Монмы (Douwe Monsma) из компании «Кембридж НаноТех» (Cambridge NanoTech)
показала, что спин может быть транспортирован (перемещен) на марафонскую по меркам
микроэлектроники дистанцию – 350 мкм!!! – сквозь беспримесную кремниевую подложку
(использование беспримесной подложки позволяет добиться протекания «чистого»
спинового тока в полупроводнике, что очень важно для точного детектирования
результирующего сигнала).
Результаты этой пионерской работы были опубликованы 26 октября этого года в
престижнейшем физическом журнале Physical Review Letters. До этого та же группа ученых
впервые экспериментально продемонстрировала, что спиновый ток можно инжектировать
(впрыскивать) в кремниевую подложку, управлять им и измерять его (см. статью в Nature за
17 мая 2007 года).
В работе, опубликованной 13 августа 2007 года в авторитетном журнале Applied Physics
Letters, исследователи показали, как достичь очень высокой (на сегодняшний день) степени
спиновой поляризации – 37%. Это означает, что от общего числа спинов, поступивших на
инжектор, 37% однонаправленных спинов удалось доставить до детектора. Стопроцентной
поляризации соответствует случай, когда все спины, выстроенные в выделенном
направлении (чаще всего «спин-вверх»), дошли до детектора. Так как в реальных системах
есть различного рода рассеивания и поглощения (система не идеальная), стопроцентной
эффективности пока получить не удается.
Открытие подтверждает, что с кремния – рабочей лошадки современной электроники –
можно не снимать упряжку еще многие десятилетия, используя его для создания спинэлектронных устройств, таких как спиновый транзистор и спиновая память. Исследователи
показали, что кремний уже сейчас может быть использован для совершения многочисленных
манипуляций над спином на масштабе в несколько сот микрометров и в течение времени,
достаточном для осуществления нескольких тысяч логических операций (десятки
наносекунд), тем самым открывая широкую дорогу для спин электронных систем на базе
кремния. Соединив в единую схему сотни или даже тысячи созданных спиновых чипов (рис.
1, справа), можно получить сверхбыстродействующее устройство для обработки
информации, по своей эффективности превышающее современные процессоры в десятки
раз!
КАК РАБОТАЕТ СПИНОВЫЙ ТРАНЗИСТОР
Методика экспериментов, вкратце, такова. Вначале авторы изготовили слоистую структуру,
составленную из слоя ферромагнетика, слоя чистого кремния, затем второго слоя
ферромагнетика, но уже другого, и наконец слоя кремния с примесями. К разным слоям этой
структуры прикладывается специально подобранное напряжение, управляющее течением
электронов. Поток электронов на входе неполяризован, но после прохождения
ферромагнитной прослойки он приобретает поляризацию – то есть становится спиновым
113
током. Эти электроны попадают в прослойку из чистого кремния, проходят достаточно
большую дистанцию, затем попадают во второй ферромагнитный слой и выходят наружу.
Эксперименты показали, что при движении через кремний поляризация электронов частично
сохраняется. Благодаря этому, изменяя взаимную ориентацию магнитных полей в двух слоях
ферромагнетика, можно включать или выключать спиновый ток на выходе. Это позволяет
для осуществления сверхбыстрых логических операций над информацией использовать два
устойчивых состояния прибора, при которых ток либо есть (логическая «1»), либо нет
(логический «0»), по аналогии с традиционным транзистором, для осуществления
сверхбыстрых логических операций над информацией.
Вначале исследователи работали со слойками толщиной примерно 10 мкм, но в последней
статье, опубликованной в Physical Review Letters, они увеличили промежуточный слой
чистого кремния до 350 мкм – а это уже вполне макроскопический размер. Даже на таких
больших расстояниях спиновый ток по-прежнему сохранялся. Таким образом,
представленное устройство демонстрирует долгое время жизни спина электрона, за которое
он способен преодолеть слой полупроводника толщиной до 350 мкм.
Вид транзистора, принцип действия и зонная диаграмма (диаграмма энергетических
состояний барьеров, которые встречают электроны, при прохождении через вещества)
показаны на рис. 2.
Рис. 2. а – изображение кремниевого спинового транзистора, b – схема работы и c – зонная
диаграмма его компонентов. При постоянном напряжении на эмиттере Ve измерялся
«первый коллекторный ток» Ic1 на NiFe-контакте и «второй коллекторный ток» Ic2 на
индиевом контакте, осажденном на кремниевой подложке n-типа. Рис. из обсуждаемой
статьи в Phys. Rev. Lett.
На первом этапе при приложенном напряжении Ve неполяризованные электроны
инжектируются из алюминиевого эмиттера (источника) в ферромагнитный слой Co84Fe16.
114
Благодаря спин-зависимому рассеиванию электронов в магнитном слое, электроны с
выделенным направлением спина (например, «спин-вниз») отсеиваются, так как направление
намагниченности слоя Co84Fe16 не совпадает с направлением спинов. Отобранные
электроны с однонаправленными спинами туннелируют через тонкий слой Al2O3. В данном
случае туннельный барьер проходят только «горячие» электроны (с энергией, достаточно
высокой для преодоления энергетических барьеров), создавая эмиттерный ток (ток
источника). «Горячие» электроны нужны для увеличения эффективности прибора.
Пройдя через барьер Шоттки (потенциальный барьер, возникающий на границе металл–
полупроводник) в беспримесный монокристаллический слой кремния, электроны занимают
свободные места в зоне проводимости полупроводника и, под действием приложенного к
нему напряжения Vc1, начинают упорядоченное движение. При этом возникает
коллекторный ток Ic1 (ток на детекторе). После прохождения через 350-микрометровый слой
кремния, спин-поляризованные электроны детектируются вторым спиновым транзистором.
Ферромагнитный слой Ni80Fe20 регистрирует спины электронов, которые инжектируются в
кремний n-типа (то есть кремний, основными носителями тока в котором являются
электроны) для увеличения чувствительности детектора (в зоне проводимости n-типа
кремния есть избыточные электроны, которые усиливают спиновый ток), создавая
коллекторный ток Ic2. Спиновый ток зависит от относительной намагниченности обоих
ферромагнитных слоев.
3. Механизм работы инжектора и детектора. а – слои Co84Fe16 и Ni80Fe20 намагничены
параллельно, b – антипараллельно (emmiter – источник тока, F – первый и второй
ферромагнитные слои соответственно, silicon – кремниевая прослойка, collector – приемник
спинового тока).
На рис. 3 показан механизм работы детектора. В случае параллельного направления
намагниченностей в слоях Co84Fe16 и Ni80Fe20 (рис. 3а) ток выше, чем при
антипараллельном направлении
намагниченностей
(рис.
3b).
Первый
режим
функционирования детектора можно сравнить с футбольным матчем без вратаря: все мячи,
посланные в сетку ворот, оборачиваются голом. Второму же режиму соответствует игра с
очень хорошим голкипером, отражающим все летящие в ворота мячи.
Следует отметить, что при комнатной температуре транзистор всё же имеет не очень
высокую эффективность работы. Хорошие результаты работы прибор показал при
температуре –73°C (150 K). Так что исследователям еще нужно поработать над увеличением
температурных интервалов функционирования транзистора. Авторы уверены, что с
помощью их устройства вполне достижима стопроцентная спиновая поляризация, при
которой все инжектированные электроны имеют ориентацию либо «спин-вверх», либо
«спин-вниз» . Высокая степень поляризация позволяет более точно определять величину
спинового тока, избавляя логическое устройство (в данном случае подразумевается конечное
115
устройство на базе массива из спиновых транзисторов) от ошибок при анализе и обработке
информации.
Итак, создание революционного устройства – спинового транзистора на
кремнии, способного перемещать спины с выделенным направлениям на сотни
микрометров в пространстве, – состоялось, ознаменовав тем самым старт
для создания сверхбыстрой и низко энергопотребляющей электроники нового
поколения. Это первое в мире спин-электронное устройство на кремнии,
имеющее высокую степень спиновой поляризации при температуре, близкой к
комнатной. По своей важности это событие может быть сравнимо с
открытием классического полупроводникового транзистора шесть
десятилетий назад. Нам остается только пожелать исследователям новых
научных успехов и ждать появления электронной техники нового поколения.
Квантовый компьютер
1.
Введение
2.
Квантовый компьютер на ядерных спинах в кремнии
3.
Квантовый компьютер на электронном спиновом резонансе в структурах Ge–Si
Список литературы
Введение
Цифровые электронные компьютеры, широко используемые в настоящее время,
созданы с помощью полупроводниковых технологий. Такие компьютеры обычно
представляют собой совокупность элементов только с двумя возможными
логическими состояниями «0» и «1» — так называемых битов (binary digits = bits),
вентильных элементов, и соединений между ними. Такие компьютеры, в которых
логические операции производятся с этими классическими, с точки зрения физики,
состояниями в настоящее время принято называть классическими.
Однако уже достаточно давно было обнаружено, что эти классические
компьютеры не могут справиться с некоторыми очень важными задачами.
Примерами таких задач являются поиск в неструктурированной базе данных,
моделирование эволюции квантовых систем (например ядерные реакции) и,
наконец, факторизация больших чисел.
Интерес к последней задаче связан с тем, что практически все современные
шифры для секретной переписки основаны на этой математической процедуре.
Для взлома уже существующего кода необходима работа классического
компьютера в течении нескольких лет. Предполагаемое экспоненциальное
116
увеличение счёта в случае возникновения квантового компьютера сильно
встревожила «секретное» мировое сообщество и оно стала вкладывать немалые
средства в исследования и разработки в области квантового компьютера
и квантовых вычислений.
Идея квантовых вычислений впервые была высказана Ю. И. Маниным в 1980
году[1], но активно эта проблема стала обсуждаться после появления в 1982 году
статьи американского физика-теоретика Р. Фейнмана [2]. В этих работах было
предложено использовать для вычислений операции с состояниями квантовой
системы. Авторы обратили внимание на то , что каждое состояние квантовой
системы в отличие от классической может находится в состоянии суперпозиции.
В терминах классического компьютера квантовый бит (quantum bit = кубит)
в соответствии с законами квантовой механики может находиться одновременно
в состоянии «0» и «1».
Наиболее популярным в соответствующей литературе попытка объяснения этой
«странности» квантового мира производится на примере спина электрона,
наиболее ярко проявляющееся в экспериментах ядерного магнитного резонанса
(ЯМР). Это свойство электрона часто изображают в виде вращения волчка с осью
вращения, направленной вверх или вниз. Спин вверх можно принять за единицу,
спин вниз за ноль. Но оказывается можно показать математически, что электрон
может также находиться в «призрачном» двойном состоянии, состоянии
СУПЕРПОЗИЦИИ, В КОТОРОМ СПИН КАК БЫ СМОТРИТ ОДНОВРЕМЕННО
ВВЕРХ И ВНИЗ. Это в свою очередь означает что это состояние есть
одновременно ноль и единица. Если теперь выполнять вычисление с помощью
этого электрона, то они будут выполняться с одновременным использованием
нуля и единицы, то есть два вычислительных действия так сказать «за цену
одного»!
Так вот, чтобы построить квантовый компьютер, необходимо иметь способ
осуществлять два типа вентилей:
1) любые повороты вектора |(0)>;
2) контролируемый одним (контролирующим) кубитом поворот другого
(контролируемого) кубита [4]. Повороты кубита выполняются под воздействием
внешнего резонансного поля. Квантовая эволюция состояния кубита
|(t)> совершается согласно уравнению Шредингера
где
— энергия взаимодействия дипольного момента  кубита и внешнего
резонансного электрического поля (например, лазера). Приведенное уравнение
легко
решается
и дает
результат:
117
Пусть в начальный момент кубит находится в состоянии |0> (т. е. a(0)=1, b(0)=0).
Тогда
а вероятность
найти
кубит
в момент
t в состояниях
|0> и
|1> равны
Это показывает, что кубит с частотой  (частота Раби) переходит из состояния
|0> в состояние |1>, а в промежуточные моменты времени находится в состоянии,
описываемом суперпозицией |(t)>=a(t)|0>+b(t)|1>. Контролируя длительность и
фазу внешнего воздействия, мы можем получить кубит в состоянии, описываемом
любой суперпозицией.
Рис. 1. Зависимость состояния кубита от длительности и фазы внешнего воздействия.
Переворот спина квантово-механической двухуровневой частицы может
произойти под влиянием внешнего ВЧ резонансного поля или поля лазера.
118
Рис. 2. Управляемая квантовая эволюция двухуровневой системы под влиянием
резонансного поля — метод реализации квантовых вычислительных процессов.
внешнего
Итак, предполагаемые преимущества квантового компьютера перед классическим
заключаются в том, что в отличие от последних квантовый компьютер оперирует
при вычислениях не с числами, а с квантовыми состояниями.
Далее отметим, что в классической физике индивидуальные состояния частиц
объединяются при помощи обычного скалярного произведения. При этом
возможное число состояний из n частиц образует векторное пространство
размерностью 2n.
В квантовой системе состояние квантовой частицы «квантового бита» (КУБИТА)
может быть выражено через суперпозицию базисных состояний (суперпозицию
|0> и |1>) и поэтому квантовые состояния объединяются при помощи умножения
тензоров.
Результирующее пространство состояний из n квантовых частиц обладает при
этом размерностью 2 n.
Итак, в предполагаемых квантовых компьютерах экспоненциальное увеличение
пространства состояний требует всего лишь линейного увеличения физического
пространства (т. е. увеличения n частиц ).
Всё это означает, что если один кубит может быть одновременно в двух
суперпозиционных состояниях — 0 и 1, то два кубита могут быть уже в четырёх
суперпозиционных состояниях — 00, 01, 10, и 11, представляя четыре числа
сразу!
Видно, что увеличение растёт экспоненциально: на m кубитах можно выполнять
одновременно вычисление над 2m числами параллельно. Это значит, что используя
всего несколько сотен кубитов, можно представить одновременно больше чисел,
чем имеется атомов во вселенной. Это также позволяет предполагать такое же
увеличение скорости вычислений квантового компьютера по сравнению
с классическим. Это предположение основано на том, что при квантовых
вычислениях элементарным шагом является отдельная унитарная операция над
m — кубитной суперпозицией — принцип квантового параллелизма. Иначе
говоря, когда в классическом компьютере вычисляется единственное выходное
119
значение для одного входного, в квантовом компьютере вычисляются выходные
значения для всех входных состояний. Именно этот процесс и принято называть
квантовым параллелизмом.
Более подробное и полное изложение вопроса о теоретическом обосновании
и принципах действия квантового компьютера, а также о проведении квантовых
вычислений, можно найти прежде всего в первой книге на русском языке
изданной в нашей стране по этой тематике, написанной К. А. Валиевым
и А. А. Кокиным [3]. [Один из авторов — академик РАН, К. А. Валиев был один
из первых, кто осознал важность проблемы квантового компьютера в развитии
современных информационных технологиях. Кроме [3], им опубликовано много
работ в периодической печати по вопросам КК и прочитано огромное количество
докладов на научных собраниях самого высокого уровня. В процессе изложения
представляемого в данной главе материала мы широко используем содержание
этих докладов,(конечно любезного разрешения автора).] Тем, кто захочет
получить ещё более полную информацию по этому вопросу авторы рекомендуют
для изучения ещё несколько публикаций на русском языке [4, 5, 6].
Несмотря на всю привлекательность преимуществ предполагаемого квантового
компьютера вопрос о реальной возможности его использования долгое время
оставался открытым. Однако, за последние несколько лет состояние дел в этой
области существенно продвинулось. Можно указать на несколько причин,
по которым интерес к квантовому компьютеру резко увеличился.
1. Разработаны квантовые алгоритмы для решения упомянутых ранее наиболее
трудных задач (например, для факторизации больших чисел P. W. Shor [7] и для
поиска в неструктурированной базе данных L. K. Grover [8].
2. Разработана процедура коррекции квантовых ошибок [9], без которой
практически невозможны попытки создавать квантовый компьютер.
3. Продемонстрирована экспериментально возможность квантовых вычислений
на основе алгоритма Гровера и др. на жидкостных ядерных магнитно —
резонансных (ЯМР) квантовых компьютерах [10], [11], [12], [13].
4. Предложены реалистичные варианты конструкций квантовых компьютеров
на основе твёрдотельных элементов:
o
а) на основе квантовых точек (D. Loss, [14], G. Burkard, [15],
L. Fedichkin, K. Valiev [16];
o
б) на основе сверхпроводящих переходов Джозефсона (D. V. Averin,
1998) [17]];
o
в) на ядерных спинах донорных атомов фосфора 31Р в изотопически
чистом 28Si (B. E. Kane [18];
o
г) на электронных спинах тех же атомов фосфора в эпитаксиальных
гетероструктурах Ge1-xSix D. DiVincenzo [19].
В двух посдледних работах в качестве прообраза квантового компьютера
предложены нанометровые транзисторные структуры, с предполагаемым
использованием всех технологий наноэлектроники, описанных в настоящем
120
издании. Но в случае реализации таких систем в качестве кубитов необходимо
выполнить ряд дополнительных условий (требований), необходимых для работы
квантового компьютера.
Как следует из всего вышесказанного квантовый компьютер должен состоять
из квантовых частиц-кубитов, которые можно рассматривать. как единичные
вектора в двухмерном комплексном векторном пространстве, с ортогональным
зафиксированным базисом |0> и |1>.
Кубитом может быть любая двухуровневая квантовая система. Простейшей
системой с двумя состояниями является квантовая частица со спином 1\2
в постоянном магнитном поле. Такой частицей может быть как электрон, так
и ядро. Безусловно, при измерениях состояния |0> или |1> должны быть физически
различимы, то есть спиновое состояние должно быть каким либо образом
измерено.
Теперь можно сформулировать наиболее общие условия создания твёрдотельного
(полупроводникового) квантового компьютера на электронных (ядерных ) спинах.
Для реализации такого компьютера необходимо:
— наличие ансамбля (регистра) кубитов;
— наличие постоянного магнитного поля, снимающего вырождение по спину —
ΔEe=μBgeB (ΔEN=μNgNB), где B — магнитное поле, μB — магнетон Бора, μN —
ядерный магнетон, ge(N) — электронный (ядерный), g-фактор;
— низкие температуры, приводящие перед началом работы все кубиты в нижнее
(основное) состояние (делающая все электроны спин — поляризованными)
и предотвращающая неконтролируемые переходы с нижних уровней на верхние
(сопровождаемые переворотом спина!);
— возможность проведения индивидуализации кубитов, с помощью напряжения
на специальные операционные затворы одноэлектронных транзисторов;
— возможность подачи импульсов высокочастотного электромагнитного
излучения различной длительности и фазы для поворота спина на заданный угол;
— реализация нанометровых (~100-1000А) расстояний между кубитами, для
организации взаимодействия между ними;
— возможность проведения однокубитных и двухкубитных логических операций
с помощью затвора связи между кубитами.
2. Квантовый компьютер на ядерных спинах
в кремнии
2А. Конструкция кубита
2Б. Индивидуализация кубитов и однокубитные операции
121
2В. Взаимодействие кубитов и двухкубитные операции
2А. Конструкция кубита.
Все эти требования были учтены B. Kane [17] в его конструкции квантового
компьютера (КК) на основе кремния, причём условия реализации такого прибора
безусловно возможна только с использованием всех достижений нанометровой
кремниевой планарной технологии ИС.
Важным требованием при создании такого КК является изоляция кубитов
от любых степеней свободы, которые могут вести к декогерентности. Если
кубитами
являются
спины
на доноре
в полупроводнике,
ядерные
спины в матрице представляют из себя большой резервуар, с которым донорные
спины могут взаимодействовать. Следовательно, матрица должна содержать ядра
со спином I=0. Это требование исключает все полупроводники А3В5 из числа
кандидатов на матрицу, так как ни один из составляющих их элементов не имеет
стабильных изотопов с нулевым спином. Для кремния такой изотоп
существует: 28Si. Кроме того, для кремния наиболее развита технология
получения материала, имеется большой опыт в создании нанообъектов, так что
он лучше всех подходит на роль полупроводниковой матрицы.
Рис. 3. Два кубита в одномерном регистре, содержащие два 31Р донора со связанными
электронами, внедрёнными в 28Si. Они отделены от управляющих металлических затворов
на поверхности слоем SiO2.
А — электроды управляют (задают) резонансную частоту ядерно — спинового кубита. J — затворы
управляют взаимодействием между электронами соседних ядерных спинов.
Единственным мелким донором в Si со спином I=1/2 является 31Р. Система Si:31Р
была исчерпывающе изучена 40 лет назад в экспериментах по электрон-ядерному
двойному резонансу. При достаточно низкой концентрации 31Р и при
Т=1,5 К время релаксации электронного спина порядка тысяч секунд, а время
релаксации ядерного спина 31Р превышает 10 часов. По-видимому, при
температуре в области милликельвинов время релаксации 31Р, ограниченное
фононами, будет порядка 1018 секунд, что делает эту систему идеальной в этом
смысле для квантовых вычислений. Условия, необходимые для вычислений при
122
помощи ядерных спинов, могут возникнуть, если ядерный спин локализован
на положительно заряженном доноре в матрице полупроводника, следовательно,
температура должна быть настолько низкой, чтобы исключить ионизацию
донора. Волновая функция электрона тогда концентрируется у ядра донора (для
s-орбиталей и энергетически зон, образованных из них), приводя к большой
энергии сверхтонкого взаимодействия между спином ядра и спином электрона.
По расчетам Кейна необходимая температура для работы должна быть менее
0.1 К. Пластина кремния при этой температуре помещается в постоянное
магнитное поле В0 2 Т (рис. 3). В этих условиях электроны будут практически
полностью спин-поляризованы (n↑/n↓<10—6), а ядерные спины будут
упорядочиваться по мере взаимодействия с электронами.
2Б. Индивидуализация кубитов и однокубитные операции.
Между спинами электрона и ядра существует сверхтонкое взаимодействие,
определяемое контактным взаимодействием Ферми. С учетом взаимодействия
спи-нов с магнитным полем разностная энергия между двумя ядерными
уровнями может быть записана, как:
(1)
где
А
—
энергия
сверхтонкого
взаимодействия,
и
|(0)|2 — плотность вероятности волновой функции электрона, определенная
вблизи ядра, а A резонансная частота. Из формулы (1) видно, что резонансная
частота зависит как от энергии сверхтонкого взаимодействия, так и от величины
магнитного поля.
123
Рис. 4. Электрическое поле, приложенное к А — затвору, смещает (вытягивает) волновую функцию
электрона от донора по направлению к барьеру, снижая сверхтонкое взаимодействие и
соответственно резонансную частоту ядер.
Кейн предложил для индивидуализации кубитов создать систему А-затворов, к
которым прикладывается напряжение различной величины и полярности.
Как видно из рис. 4., электрическое поле, приложенное к системе, сдвигает
волновую функцию электрона от ядра и уменьшает сверхтонкое взаимодействие,
что приводит к сдвигу резонансной частоты. Величина этого сдвига
в соответствии с расчетом Штарковского расщепления проведенного Kohn'ом для
мелкого донора в кремнии, находящегося под затвором на глубине 200 А, и
показана на рис. 4.
Таким образом, приложение напряжения к затвору А приводит к изменению
резонансной частоты, вследствие чего спины могут быть селективно приведены в
резонанс с Вac, что позволяет проводить одновременные, произвольные вращения
каждого ядерного спина, т. е. осуществлять однокубитные операции.
2В. Взаимодействие кубитов и двухкубитные операции.
Двухкубитные
операции
(<УПРАВЛЯЕМОЕ
НЕ>
и
<ДВАЖДЫ
УПРАВЛЯЕМОЕ НЕ>) в принципе осуществимы, если соседние кубиты
взаимодействуют. Взаимодействие между ядерными спинами возникает
опосредованно из-за взаимодействия электронов соседних кубитов, когда доноры
расположены достаточно близко друг к другу и волновые функции электронов
перекрываются.
124
Гамильтониан дважды связанной системы донорное ядро — электрон (два
кубита) для энергии меньшей, чем энергия связи донор-электрон, записывается
как:
,
где Н(В) — член взаимодействия магнитного поля со спинами, А1 и А2 — энергии
сверхтонкого взаимодействия соответствующих систем ядро-электрон,  —
спиновые матрицы Паули, индексы 1 и 2 относятся к первому и второму кубиту,
индексы e и n — к электрону и ядру, а 4J — обменная энергия, которая зависит от
перекрытия волновых функций электронов. Для хорошо разделенных доноров:
(2)
где r — расстояние между донорами,  — диэлектрическая постоянная
полупроводника, и аB — Боровский радиус.
Изменение обменной частоты от расстояния между донорами, рассчитанная для
кремния, изображена на рис. 5. Уравнение (2), вообще-то справедливо для
атомов водорода. В кремнии усложняется из-за вырожденной анизотропной
структуры его долин. Обменные члены от каждой долины интерферируют, что
приводит к осциллирующей зависимости J(r). В этой работе сложности,
связанные
с
зонной
структурой
кремния,
не
учитываются.
Рис. 5. Напряжение на электроде J — изменяет электростатический потенциальный барьер между
донорами, увеличивая или уменьшая обменное взаимодействие, пропорциональное перекрытию
волновых функций. На рисунке изображена зависимость обменной частоты — 4J/hдля кремния, от
расстояния между донорами, когда V=0.
125
При расчете J(r) на рис. 5 использовались значения эффективной массы в Si
me=0.2 m0 и боровского радиуса aB=30 А. Поскольку J пропорциональна
перекрытию волновой функции электронов, она может изменяться за счет
электростатического потенциала, приложенного к «J-затвору», расположенному
между доноров. Как будет показано ниже, значительная связь между ядрами
будет
осуществляться,
когда
,
и это условие требует разделения между донорами на расстояние 100—200 А.
Однако в действительности это расстояние может быть больше, так как к «Jзатвору» может быть приложен положительный потенциал, который уменьшает
барьер между донорами. Размеры затвора, необходимые для КК близки к
ограничению электронной технологии.
Таким образом, приложение напряжения к затвору J приводит
волновых функций электронов, вследствие чего переворот
из электронов осуществляется (или не осуществляется)
от состояния спина второго электрона, что позволяет
двухкубитные операции.
к перекрытию
спина одного
в зависимости
осуществлять
Метод для детектирования спинового состояния электрона при использовании
электронных средств показан на рис. 6.
Рис. 6. Только ↑↓ — ↓↑ электроны могут совершать переходы в состояния, в которых электроны
связаны с одним и тем же донором (принцип Паули !) создавая D — состояния. Электронный ток
(заряд) во время этих переходов измеряется с помощью емкостной техники (одноэлектронный
транзистор), что делает возможным определение спинового состояния электрона и ядра.
Оба электрона могут быть связаны на одном и том же доноре (D — состояние),
если к А-затворам приложено соответствующее напряжение. В Si:P D —
состояние всегда синглетное с энергией связи второго электрона 1,7 мэВ.
Следовательно, дифференциальное напряжение, приложенное к А-затворам,
может вызывать движение заряда между донорами, что возможно только в том
случае, когда электроны находятся в синглетном состоянии. Если электроны
находятся в различном состоянии, то под вторым электродом может оказаться
два электрона (принцип Паули!) — заряд окажется равен 2е. В противном случае
имеем единичный заряд электрона. Движение заряда можно измерить, используя
одноэлектронную емкостную технику. Такой подход к измерениям спина дает
сигнал во все время релаксации спина, которое может достигать в Si:P тысяч
секунд.
126
Таким образом, определение спинового состояния в связанной системе двух
электронов производится по измерению заряда, когда оба связаны в D —
состоянии. Это возможно, когда они находятся в синглетном состоянии
(с разными спинами). Для проведения двухкубитных операций расстояние между
донорами должно составлять 100—200 А
3. Квантовый Компьютер на электронном спиновом
резонансе в структурах Ge–Si (D. Di Vincenzo, 1999)
3.1. Отличия квантового компьютера с электронным спиновым резонансом
3.2. Конструкция ЭСР кубита
3.3 Однокубитные операции
3.4 Двухкубитные операции
3.5 Детектирование спинового резонанса МДП транзисторами
3.6 Влияние ориентации подложки кремния
В данной работе идеи, предложенные в работе Кейна, получили дальнейшее
развитие, а само создание КК стало вещью более реальной.
3.1. Отличия КК с электронным спиновым резонансом.
Основные новые предложения этой работы сводятся к следующему:

Используется электронный спин, что предпочтительнее использования
ядерного спина. Работая с электронным спином, мы удовлетворяем
требованиям тонкого спинового перехода между электронами и ядром
для ввода и считывания квантовых данных. В магнитном поле B 2 Тл
частота ЭСР равна 56 ГГц и из-за высокой Зеемановской энергии
электронные спины позволяют работать вплоть до частот в гигагерцовом
диапазоне, в то время как ядерные спины — только до 75 кГц. При Т=1К
электронные спины (в отличие от ядерных) полностью поляризованы.
Кроме
того,
чистота
изотопа
матрицы
кремния
не критична
для
электронных спинов.

Вместо кремния используются эпитаксиальные Si/Ge гетероструктуры
(ГС), электронной структурой которых можно управлять путем изменения
состава. Эти напряженные ГС, производство которых сейчас широко
127
развивается
во всем
технологии
и
мире,
находятся
в главном
время
используются
в настоящее
русле
кремниевой
для производства
высокочастотных компонентов беспроволочной связи. В композиционно
модулированной Si/Ge ГС из-за разницы в электронном g-факторе (g=1.995
для Si и g=1.563 для Ge) электронный спиновой резонанс (ЭСР) может
подстраиваться
электростатическим
затвором,
а
возможность
искусственного создания необходимой энергетической структуры зоны
проводимости позволяет выделить барьерные области. Самое главное
заключается в том, что в Si/Ge ГС можно управлять эффективной массой
донорного электрона: Боровский радиус связанного электрона в Si/Ge может
быть много больше, чем в кремнии из-за малой эффективной массы
в напряженных ГС и большей диэлектрической проницаемостью. Это
снижает требования к литографии до уровня существующей электроннолучевой литографии и даже до уровня современной оптической литографии
(до 2000 А и больше).

Исключены J-затворы.

Для того, чтобы прочесть финальные результаты компьютерных
расчетов,
предлагают
детектировать
заряд
одиночных
электронов.
Предполагается, что это может быть сделано обычными полевыми
транзисторами при низких температурах, что избавляет от применения
одноэлектронных транзисторов.
3.2. Конструкция ЭСР кубита.
Рассмотрим строение ячейки из двух кубитов предлагаемого КК (рис. 8).
На кремниевой подложке методом МЛЭ выращивается буферный слой
твердого раствора Si/Ge, на котором последовательно размещаются еще
пять
рабочих
слоев,
состав
и
толщина
которых
определяется
необходимой энергетической диаграммой (левая часть рисунка) и
требованиями по эффективному воздействию управляющих затворов.
Основными
слоями,
в которых
проходят
128
квантовые
вычисления,
являются слои D2 (второй донорный слой) и <настроечный> (tuning) слой
T. В слое D2 размещаются атомы 31Р на расстоянии 2000 А друг от друга.
Связанные с этими атомами электроны и выполняют роль кубитов. Слои
D2 и T отличаются составом и поэтому имеют разный g-фактор: для слоя
D2 он составляет 1,995, а для слоя Т — 1,563. Слои D2 и T заключены
между двумя барьерными слоями В, которые ограничивают перемещение
электрона в вертикальном направлении.
.
7. Строение
ячейки
ЭСР
состоящей
а)
Изменение
ширины
запрещенной
зоны
из
двух
в
кубитов.
эпитаксиальной
гетероструктуреGe1-xSix.
б) Поперечный разрез двухкубитной ячейки.
Это ограничение определяется разрывами зоны проводимости между
слоями D2 и В, и Т, и В, которые равны 20 мэВ. Ограничение барьером
играет важную роль. Оно сохраняет кубитные донорные электроны
в течение долгого времени, не допуская потерь как носителей, так и
квантовой информации. Для этого толщина барьера составляет
200 А,
при этом время жизни сравнимо с временем спин-решеточной релаксации
Т1 ( 1 час). Оба слоя толщиной 400 А согласуются с пределом,
ограниченным напряжениями
1000 А для х=0,23. Слои D и T имеют
129
тол-щину сравнимую с aB,z — вертикальным Боровским радиусом и
вносят слабый вклад в возникающие напряжения. Очень важно, что
между слоями D2 и Т разрыв зон равен нулю, так что нет препятствий для
перемещения электрона из слоя D2 в слой. В слое D1 (первый донорный
слой) перпендикулярно плоскости рисунка размещены каналы МДП
транзисторов, которые служат для регистрации сигнала в конце
вычислений и пространственно расположены под атомами фосфора.
3.3. Однокубитные операции.
Сущность однокубитных операций заключается в том, что затвор может
управлять частотой спинового резонанса. Так же, как и в КК Кейна,
волновая функция электрона за счет электростатического притяжения,
вызванного напряжением затвора, сдвигается в сторону затвора, что
изменяет энергию сверхтонкого взаимодействия и резонансную частоту.
Но, кроме того, волновая функция электрона проникает в Т-слой с
составом Si0,15Ge0,85, где g-фактор меньше, чем в D1 слое, что вызывает
дополнительное изменение энергии сверхтонкого взаимодействия и
резонансной частоты (Рис. 8). На рисунке хорошо видно, что изменение
напряжения в средней части диапазона даёт возможность изменять
резонансную частоту в широких пределах. Интервал соответствующий gфактору
равному
1.563
используется,
для организации двух-кубитных операций.
130
как
мы
увидим
далее
Рис.
8. Схематическая
зависимость
спин-резонансной
частоты
от напряжения на управляющем электроде кубита [18].
3.4. Двухкубитные операции.
Как уже говорилось, кубиты должны быть расположены достаточно
далеко друг от друга, чтобы не осуществлялось взаимное влияние и
внесение фазовых ошибок. В то же время для двухкубитных операций
необходимо, чтобы было возможно перекрытие волновых функций и
обменное взаимодействие между кубитами. В модели Кейна перекрытие
достигалось путем введения J-затворов. В данной работе обменное
взаимодействие
достигается
за счет
изменения
(увеличения)
эффективного боровского радиуса в х — у-плоскости при смещении
волновой функции из слоя D1 в слой Т.
Боровский радиус — aB, водородоподобных доноров увеличивается
при уменьшении
энергии
связи,
что
напряжение на затворе (Рис. 9.).
131
происходит
при увеличении
Рис. 9. Схема организации обменного взаимодействия между
двумя кубитами (двухкубитная операция). Притягивание
электронов к слою Si 0.23 Ge 0.77 (В-барьер ), снижает их
энергию Кулоновской связи и повышает перекрытие их
волновых
функций,
разрешая
проводить
двухкубитные
операции. [19].
При этом электроны могут быть электростатически притянуты к одному
из барьеров, образованных В-слоями состава Si0,23Ge0,77, формируя тем
самым подобие модулированно легированного канала в x — y-плоскости.
Энергия связи существенно ослабевает, когда электроны проводят
большую часть времени вблизи барьера. Соответственно, кулоновский
потенциал уменьшается по формуле:
(3)
где r2=x2+y2 есть квадрат горизонтального расстояния от донора, а d —
вертикальное
расстояние
от барьера
до донора.
Таким
образом,
изменяя d, можно сделать кулоновский потенциал как угодно малым.
Малая кулоновская энергия связи означает большой боровский радиус,
что, в свою очередь, позволяет осуществлять перекрытие волновых
132
функций в x — y-плоскости вдоль барьера и двухкубитное обменное
взаимодействие.
Это
становится
возможным
при переходе
от пренебрежимо малого обменного взаимодействия по направлению
к созданию
проводящего
металлического
двумерного
газа
путем
изменения вертикального расстояния d. Всё это позволяет проводить
необходимые двухкубитные операции.
3.5. Детектирование спинового резонанса МДП транзисторами.
Как отметил В. Кейн, в [17], основной проблемой при организации
вычислений на основе управления спиновым состоянием кубита, является
детектирование спина не по его собственному магнитному моменту, но
на основании принципа Паули, то есть по зарядовому состоянию кубита.
Донорный центр может связать второй электрон с энергией 1 мэВ, при
этом этот второй электрон имеет противоположный первому спин. Таким
образом,
проблема
детектирования
спина
переходит
в проблему
детектирования заряда.
Обычные МДП транзисторы с малыми размерами способны измерить
одиночный заряд и, следовательно, и одиночный спин, но только
при низких рабочих температурах (~1 К), когда случайные перевороты
спинов исчезают, но чувствительность к одиночному заряду сохраняется.
Как показано на рис. 9, канал МДПТ расположен под атомом 31Р,
а последний, в свою очередь, под электродом затвора в слое ???. Таким
образом, спиновый кубит зажат между двумя электродами — верхним и
затвором измерительного транзистора. Как и в нормальном МДПТ,
затвор измерительного транзистора. Таким образом, последовательные
зарядовые состояния: ионизованный донор, нейтральный донор и донор
с двумя электронами (D– состояние) легко идентифицировать, измеряя
ток канала.
133
Два соседних транзистора (под соседними кубитами) имеют раздельные
чувствительные каналы, так что они могут быть раздельно опрошены,
или
даже
включены
дифференциально.
Регулировкой
затворных
электродов электроны обоих доноров могут притянуться на тот же самый
донор. Если они находятся в синглетном состоянии, они могут
объединиться, формируя D– состояние на одном из двух ионов, но
в триплетном состоянии они не могут занимать тот же самый донор.
Поскольку
одновременно
транзисторе
и
появляется
существенное
D– состояние
формируется
ионизованный
донор
изменение
D+ состояние
на одном
на другом,
дифференциального
то
тока,
достаточное для того, чтобы идентифицировать синглетное состояние.
Для триплетного состояния оба донора остаются нейтральными и
дифференциальный ток будет постоянным. Оценки показывают, мы
можем ожидать изменения тока (заряда), связанное с синглетным
состоянием,
порядка
нескольких
процентов,
что
делает
спин
наблюдаемым.
3.6. Влияние ориентации подложки кремния.
Если использовать слои Ge—Si растворов с ориентацией в направлении
<001>, то это дает ряд преимуществ. Во-первых, энергия зоны
проводимости изменяется от состава быстрее для этого направления.
Кроме того, Х2 и L-зоны пересекаются при составе примерно 90%
Ge вместо 70%, как при ориентации <111>. Это позволяет выбрать
твердые растворы с меньшими напряжениями при высоте барьера около
50 мэВ, что более чем в два раза больше, чем для ориентации <111>.
Соответственно, барьерные слои при сохранении той же вероятности
туннелирования
могут
быть
тоньше,
значительно выше.
134
а допустимые
напряжения
Кроме того, использование ориентации <001> ведет к увеличению
эффективной
массы
в плоскости
пластины
и к уменьшению
ее в направлении роста. Эллипсоид зоны проводимости расположенный
в направлении <111> отклонен на 55° от направления <001> и таким
образом
z-направление
больше
не совпадает
с тяжелой
массой
в направлении <111>. Тяжелая масса переносится (частично) в х уплоскость, что приводит к уменьшению Боровского радиуса. Однако,
самая легкая масса в Ge равна самой тяжелой массе в Si (см. Таблицу 1).
В результате слои с большим содержанием Ge будут всегда иметь в в х уплоскости
Боровский
радиус
больше,
чем
в слоях
с большим
содержанием Si. Кроме того, слои с большим содержанием Ge будут
выполнять функции туннельных Т-слоев и барьерных В-слоев точно
также, как и для направления <111>.
В работе [20] идея использования слоя с параметрами приводящими
к увеличению боровского радиуса и , следовательно к возможности
увеличения возможного расстояния между кубитами были развиты
с применением эпитаксиального нанесения активного слоя с большой
диэлектрической проницаемостью. На рис. 10. приведена конструкция
кубита использующая этот принцип.
Рис. 10. Изменение конструкции кубита по сравнению с Рис. 8.введением
слоя слоя с высокой диэлектрической проницаемостью.
135
Так как, в соответствии с выражением для боровского радиуса
его величина растёт при увеличении диэлектрической проницаемости ε
материала и с уменьшением эффективной массы m*. Такой средой может
служить твёрдый раствор
Pb1-xSnxTe (СОТ). В работе [19], были
проведены измерения диэлектрической проницаемости образца СОТ пари
различных
температурах.
Из рис. 11. видно,
что
при
понижении
температуры от 40 К до 4.2—5 К диэлектрическая проницаемость падает
от 2.105 до 2.103.
Рис.
11. Температурная
проницаемости
зависимость
СОТ от температуры.
ёмкости
1,2 —
и диэлектрической
в темноте,
3—
при
освещении.
Если теперь используя формулы (4) и (2) рассчитать зависимости
обменной частоты для различных материалов, то можно получить серию
кривых аналогичных рис. 5.
136
рис. 12. Зависимость обменной частоты двух кубитов от расстояния
между ними.
1.
Si (ε=12 , m*/m0=0,191);
2.
Ge — (ε=16 , m*/m0= 0,082);
3.
PbTe — (ε=400, m*/m0=0,05);
4.
Pb0,76Sn0,24Te (ε=2000, m*/m0=0,05).
Как видно из рисунка обменная частота для случая, когда в расчете
используются значения диэлектрической проницаемости и эффективной
массы,
соответствующие
СОТ(In)
с составом
х =0,24,
сохраняет
достаточно высокое значение даже тогда, когда расстояние между
кубитами увеличивается почти до 10 мкм.
Появились публикации о решении одной из сложнейших проблем
в создании кубита на основе ЯМР на атомах фосфора в кремнии —
точное расположение этих атомов в матрице кремния на расстояниях
всего сотни ангстрем. На Рис. 13 приведена схема процесса такого
размещения атомов, успешно применённого австралийской группой
учёных в «Центре технологии квантового компьютера» в Сиднее.
137
Рис. 13. Процесс формирования регистра фосфорных кубитов в кремнии.
Сначала производится очистка поверхности кремния в сверхвысоком
вакууме. Затем эта атомарночистая поверхность кремния (Si (001)2×1)
пассивируется монослоем водорода. Затем по специальной программе
с помощью
зонда
сканирующего
туннельного
микроскопа
(СТМ)
десорбируются в заданных местах отдельные атомы водорода. После
этого в камеру вводятся пары фосфина при давлении 10 –8 мм р.ст.
Адсорбированные молекулы фосфина затем при температуре 5000 °С
диссоциируют оставляя атомы фосфора связанные с кремнием в местах
адсорбции. После этого производится низкотемпературное заращивание
кремнием полученной структуры [20]. Параллельно с этими работами
в том же центре разработан необходимый для считывания результатов
квантовых расчётов одноэлектронный транзистор на основе структуры
Al — Al2O3. Все эти подготовительные работы в настоящее время
позволили по сообщению директора Центра создать кубит отвечающий
всем требованиям по конструкции В. Кэйна [21].
138
.
139