Задания и решения для корпоративной олимпиады БГУ Заочный тур

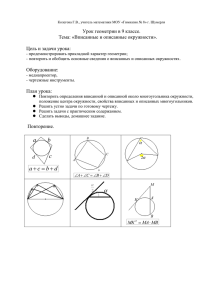
Задания и решения для корпоративной олимпиады БГУ
по математике, 10 класс, 2014 г.
Заочный тур
Задача 1.
На окружности располагаются n точек. Каждые две точки соединены отрезком,
никакие три отрезка не пересекаются в одной точке внутри окружности. Сколько при этом
образовалось треугольников с вершинами в точках пересечения отрезков внутри
окружности?
Ответ:
n!
6!( n  6)!
Решение.
1) Каждое множество из 6 точек на окружности можно единственным образом
разбить на пары точек так, чтобы соединяющие их прямые образовывали допустимый
треугольник.
Действительно, каждую из трёх прямых следует проводить так, чтобы в обеих
полуплоскостях относительно неё оставалось по две точки. Только в этом случае две
другие прямые будут пересекать первую внутри круга. Таким образом, обозначив данные
6 точек по кругу A, B, C, D, E, F, получаем единственный способ построения треугольника
с помощью прямых AD, BE и CF (рис 1).
И обратно, каждому треугольнику с вершинами во внутренних точках круга
соответствует единственное множество из 6 точек на окружности. Эти точки получаются
при пересечении с окружностью прямых, содержащих стороны треугольника.
Таким образом, искомых треугольников ровно столько, сколько существует
неупорядоченных множеств из 6 различных точек на окружности.
2) Из данных n точек на окружности требуется выбрать 6 различных точек, при
этом порядок следования точек не является существенным. Количество таких наборов
равно количеству сочетаний без повторений из n элементов по 6, то есть
n!
6!( n  6)!
B
А
C
F
E
D
Рис.1.
Задача 2.
В трапеции с основаниями a и b острые углы в сумме составляют 90, а меньшая
диагональ располагается под прямым углом к основаниям. Найти длины боковых сторон.
Ответ: √𝑎2 + 𝑎𝑏 и √𝑏 2 + 𝑎𝑏.
Решение. На рис. 2 изображена трапеция ABCD из условия задачи, AD = a, BC = b,
BAD + BCD = 90.
(1)
Ясно, что BD является меньшей диагональю трапеции. По условию, BD AD.
Обозначим BAD = α. Тогда из (1) получим BCD = 90 – α. Из треугольника DBC
получим, что BDС = α.
B
A
C
D
Рис. 2
Из треугольника АВD: BD = ADtg (BAD) = аtg α. Аналогично, из треугольника ВСD:
BD = ВСсtg (BDС) = bctg α. Приравняем правые части последних двух равенств:
𝑎
аtg α = bctg α, следовательно, tg α =√𝑏.Теперь,
cos α =
1
𝑎
√1+𝑡𝑔2 𝛼
Из треугольника АВD: AB =
Из треугольника ВСD: CD =
𝑎
𝑏
= √𝑎+𝑏, sin α= √1 − 𝑎+𝑏 = √𝑎+𝑏.
𝐴𝐷
=
cos α
𝐵𝐶
𝑠𝑖𝑛 α
=
𝑎
= √𝑎2 + 𝑎𝑏.
𝑎
√𝑎+𝑏
𝑏
= √𝑏 2 + 𝑎𝑏.
𝑏
√
𝑎+𝑏
Таким образом, АВ = √𝑎2 + 𝑎𝑏, CD = √𝑏 2 + 𝑎𝑏.
Задача 3.
Доказать, что в записи бесконечной десятичной дроби, полученной путем
следующего сложения:
0,1
0,02
0,003
0,0004
⋯
+ 0,00000008
0,000000009
0,00000000010
0,000000000011
⋯
нет ни одной цифры 8.
Решение.
Рассмотрим сумму
S= 0,1+ 0,02+ 0,003+ 0,0004+ …
0,1S=
0,01+ 0,002+ 0,0003+ …
0,9S=S-0,1S= 0,1+ 0,01+ 0,001+ 0,0001+ …
Таким образом, 0,9S равно сумме убывающей геометрической прогрессии с
0,1
1
1
10
первым членом 0,1 и знаменателем 0,1. Тогда 0,9S=
 . Значит, S=
 
1  0,1 9
9  0,9 81
0,123456790123456790…=0,12345679(012345679) – периодическая десятичная дробь, не
содержащая цифры 8.
Задача 4.
Перечислить все натуральные числа a и b такие, что в десятичной записи числа aa
содержится b цифр, а в десятичной записи числа bb – a цифр.
Ответ: 1,8 и 9.
Решение.
Обоснуем, что если такиеa и b найдутся, то a = b. Допустим, что a >b. Тогда
aa >ba > bb. С другой стороны, так как по условию число aa состоит из b цифр, то
оно меньше числа bb, состоящего из а цифр. Противоречие. Аналогичным образом
исключаем случай a <b.Значит, если числа a и b, удовлетворяющие условию задачи,
существуют, то a = b. Выясним, при каких а число aaсостоит из a цифр.
Число N состоит из n цифр, если выполняются неравенства 10n-1  N < 10n. Значит,
если число aa состоит из a цифр, то a < 10. В самом деле, если a ≥ 10, то aa ≥ 10a, и число
aa содержит не менее чем a + 1 цифру. Далее:
11 = 1, 22 = 4, 33 = 27, 44 = 256, 55 = 3125,
66 = 363< 403 = 43103 = 64103<105,
77 = 7493<7503 = 753103 = 875103<106,
108> 88 = 644> 604= 64104 = 362104> 107,
109>99 = 9814>984104 = 9642104>962106>108.
Из рассмотренных соотношений следует, что условиям задачи удовлетворяют лишь
а = 1, 8 и 9.
Задача 5.
Несколько учеников 10 класса в течении 4 минут наблюдали за этапом эстафеты
Олимпийского огня в г. Брянске. Каждый наблюдал за ней ровно 1 минуту и заметил, что
за это время факелоносец пробежал ровно 10 метров (бег проходил неравномерно, с
остановками для приветствия зрителей). Ни в один момент времени эстафета не
оставалась без наблюдения. Какой наибольший и какой наименьший путь мог пробежать
факелоносец за эти 4 минуты?
Решение. 1) На рис. 3 показано возможное расположение наблюдателей и
движение факелоносца, такое, что за 4 минуты он пробежал 60 метров.
Путь (м)
60
50
40
30
20
10
Время (мин)
наблюдатель А1
1
наблюдатель А2
наблюдатель А3
2
3
наблюдатель А5
4
наблюдатель А6
наблюдатель А4
Рис. 3
2) Докажем, что при этом достигается максимальное перемещение факелоносца.
Пусть А1 — первый наблюдатель. Рассмотрим всех наблюдателей, которые начали
следить за эстафетой либо в тот момент, когда закончил А1, либо ещё раньше (по условию
такие наблюдатели есть). Пусть А2 — последний из таких наблюдателей. Теперь
рассмотрим всех наблюдателей, начавших следить за факелоносцем не позже, чем
закончил А2, и обозначим через А3 последнего из них. Аналогично выберем наблюдателя
А4 и т. д. Ясно, что в итоге мы дойдём до наблюдателя, окончившего наблюдать ровно в
конце последней минуты (если наблюдатель Ак окончил наблюдать раньше, то имеются
наблюдатели, начавшие следить позже, чем начал Ак, и тогда можно выбрать наблюдателя
Ак+1).
Пусть А1, А2, ..., Аk — выбранные таким образом наблюдатели. Понятно, что
промежутки наблюдения «нечётных» наблюдателей не пересекаются, точно так же не
пересекаются промежутки, в которых следили «чётные» наблюдатели.
В самом деле, если бы нашёлся момент времени в который одновременно
наблюдали А1 и А3, то это значило бы, что наблюдатель А2 выбран неправильно, поскольку
наблюдатель А3 начал наблюдать позже, чем начал А2, но ещё до того, как закончил А1.
Так как промежутки наблюдения А1, А3, ... не пересекаются, то этих наблюдателей за 4
минуты меньше 4. Поэтому их не больше 3. Этим же числом ограничивается количество
наблюдателей «чётной» группы. Таким образом, 60 метров — максимально возможное
перемещение факелоносца за 4 минуты.
3) Выясним, каким может быть минимальный путь факелоносца. Для этого
рассмотрим всех «нечётных» наблюдателей и найдём их минимально возможное
количество. Поскольку все временные промежутки между соседними «нечётными»
наблюдателями меньше одной минуты, то число «нечётных» наблюдателей не должно
быть больше 2. Отсюда следует, что факелоносец не мог пробежать меньше 30 метров.
Задача 6.
5 5𝜋
Найдите множество значений функции y=sin2x, если x[arсcos 13 ; 12 ].
Решение.
5 5𝜋
1) x[arcos 13 ; 12 ], следовательно, х лежит в первой четверти.
2) Поскольку х лежит в первой четверти, то 2x 
5
1
5𝜋
6
5
1
 . Так как 13 < 2 и арккосинус
5
1
2π
убывает в первой четверти, то arсcos 13 > arсcos 2; 2arсcos 13 > 2arсcos 2 = 3 ,
следовательно, 2х находится во второй четверти.
3) Во второй четверти функция синус убывает и непрерывна. Значит, данная
5π
5
функция y=sin2x принимает все значения от у(12) до у(arсcos 13).
4) Вычислим эти значения: sin
5
5π
6
π
1
= sin 6 = 2;
5
5
25
5
120
sin(2arсcos 13) = 2sin(arсcos 13) cos(arсcos 13) = 2√1 − 169 ∙ 13 = 169.
1
Ответ: [2 ;
120
169
].
Задача 7.
График функции y=x2 был изображен в системе координат Oxy, затем
координатные оси были стерты. Как, пользуясь лишь циркулем, линейкой и оставшейся
на чертеже параболой, восстановить координатные оси и длину единичного отрезка?
Решение.
При помощи циркуля и линейки выполним следующие построения (рис.4).
1) Проведем две параллельные прямые, пересекающие параболу в точках A, B, C,
D. Проведем прямую l через середины E и F отрезков AB и CD. Прямая l параллельна оси
Oy.
Действительно, если прямая имеет уравнение y = kx+b, то абсциссы x1 и x2 точек её
пересечения с параболой являются корнями уравнения x2= kx+b или x2–kx+b=0. По
теореме Виета, x1+x2=k. Значит, сумма абсцисс точек A и B равна k. Тогда абсцисса точки
E, как середины отрезка AB, равна
x1  x2
2

k
2
. Аналогично, абсцисса точки F равна
k
2
.
Значит, прямая l=EF параллельна Oy.
2) Проведем прямую m перпендикулярно l. Найдем середину S отрезка прямой m,
заключенного внутри параболы. Через точку S проведем прямую, параллельную прямой l.
Эта прямая совпадает с Oy, так Oy – ось симметрии параболы. Точка O пересечения Oy с
параболой – начало координат. Через точку O проведем прямую, перпендикулярную OS.
Эта прямая совпадает с Ox.
3) Для нахождения длины единичного отрезка построим биссектрису угла xOy. Она
пересекает параболу в точке с координатами (1; 1). Построив перпендикуляр к Ox,
проходящий через эту точку, найдем длину единичного отрезка.
y
l
B
S
m
E D
A
F
C
x
O
1
Рис. 4
Задача 8.
Львы охотятся за антилопой на участке саванны, имеющем форму шахматной
доски 8×8 клеток. Все участники охоты за один ход могут передвигаться на одну клетку
по вертикали или по горизонтали. Вначале ходит антилопа, затем делает ход каждый из
львов, независимо друг от друга.
Если антилопа окажется на краю участка, то на следующем ходу она спрыгнет с
него и спасется от львов. Если лев оказывается на одной клетке с антилопой, он ловит ее.
1. Если антилопа уже стоит на одной из клеток внутри участка (не крайних), то
могут ли два льва расположиться на крайних клетках участка так, чтобы они поймали
антилопу?
2. Пусть охотятся три льва, но антилопа в первый раз может сделать два хода один
за другим. Доказать, что антилопа спасется от львов, независимо от того, как все
участники расположились на участке перед охотой.
Решение.
1. Пусть антилопа стоит на не крайней клетке участка. Через эту клетку можно
провести две диагонали. Выберем любую из них и поставим двух львов на концы
диагонали (рис. 5). После хода антилопы львы должны сдвигаться так, чтобы оказаться
снова с антилопой на одной диагонали, параллельной исходной. При этом количество
клеток по диагонали между львами и антилопой уменьшается на одну. Если вначале оно
было равно k, то не более чем через k шагов ближайший по диагонали лев поймает
антилопу. При этом, на какой бы внутренней клетке участка не стояла антилопа вначале,
минимальное количество ходов, нужных, чтобы спрыгнуть с участка, всегда на один
больше, чем расстояние k по диагонали до ближайшего льва. Даже если антилопа
достигает края участка, на следующем ходу ее ловит один из львов.
Л
А
Л
Рис. 5
2. Разделим участок на четыре части двумя диагоналями, проходящими через
клетку, на которой стоит антилопа. Так как львов всего три, то в одной из четырех
образовавшихся частей участка нет ни одного льва. Внутри такой части (на рис. 6 это,
например, правая часть) антилопа может двигаться по горизонтали к краю участка. После
двух её первых ходов видно, что клетки выделенной части участка, определённой новым
положением антилопы, недостижимы для львов за один ход. При любом движении львов,
после следующего хода антилопы это свойство будет сохраняться. Таким образом,
антилопа достигнет края участка и спрыгнет с него.
Л
Л
А
Л
Рис. 6